1 Introduction
The Weibel instability, which is mainly characterized as being able to generate strong magnetic fields, is of great significance for a range of scenarios in plasma physics, and has been studied for many decades since it was first proposed[Reference Weibel1–Reference Jung, Osterholz, Lowenbruck, Kiselev, Pretzler, Pukhov, Willi, Kar, Borghesi, Nazarov, Karsch, Clarke and Neely4]. For example, in astrophysics, the magnetic field generated in the Weibel instability is believed to be the leading mechanism for shock formation in weakly magnetized plasmas[Reference Fiuza, Fonseca, Tonge, Mori and Silva5, Reference Gruzinov and Waxman6]. While in inertial confinement fusion, the magnetic field generated by the Weibel instability is found to play an important role in the transport of fast electrons and the thermal isotropization of energy flows[Reference Ren, Tzoufras, Tsung, Mori, Amorini, Fonseca, Silva, Adam and Heron7–Reference Hao, Ding, Sheng, Ren, Kong, Mu and Zhang11].
The classical Weibel instability, which is referred as the thermal anisotropy-driven Weibel instability, arises from electron thermal anisotropy and can increase when a plasma slab is expanding into the vacuum[Reference Stockem, Dieckmann and Schlickeiser12]. Besides, the Weibel instability can also be driven by an ion flow, which includes a counterstreaming ion flow but a collisional and isotropic electron population, referred as the ion-driven Weibel instability[Reference Stockem, Grismayer, Fonseca and Silva13]. Both kinds of instability could result in current filaments longitudinal to the electron or ion flow, and toroidal magnetic fields around the current filaments[Reference Tzoufras, Ren, Tsung, Tonge, Mori, Fiore, Fonseca and Silva14, Reference Thaury, Mora, Héron, Adam and Antonsen15]. The strength and spatial wavelength in the transversal plane of the magnetic field are key parameters for the estimation of other important processes, such as shock formation and electron transport, and are often seen as direct characteristics for judgment of the growth stage of the Weibel instability[Reference Thaury, Mora, Héron, Adam and Antonsen15].
Experimentally, when space charge effects between the current filaments have a negligible impact on deflection of the probe proton, which has been proved using the difference in deflection between the electric field and the magnetic field, the magnetic field generated by the Weibel instability can be transversely imaged by proton radiography[Reference Kugland, Ryutov, Chang, Drake, Fikse, Froula, Glenzer, Gregori, Grosskopf, Koenig, Kuramitsu, Kuranz, Levy, Liang, Meinecke, Miniati, Morita, Pelka, Plechaty, Presura, Ravasio, Remington, Reville, Ross, Sakawa, Spitkovsky, Takabe and Park16–Reference Quinn, Romagnani, Ramakrishna, Sarri, Dieckmann, Wilson, Fuchs, Lancia, Pipah, Toncian, Willi, Clarke, Notley, Macchi and Borghesi18]. The emergence of the Weibel instability is then manifested as striations on the proton images. The amount and spatial wavelength of the proton flux striations, which are related to the amount and spatial wavelength of the current filaments, are used to indicate the evolution of the instability, such as growth, saturation and coalescence of the current filaments[Reference Fox, Fiksel, Bhattacharjee, Chang, Germaschewski, Hu and Nilson3, Reference Quinn, Romagnani, Ramakrishna, Sarri, Dieckmann, Wilson, Fuchs, Lancia, Pipah, Toncian, Willi, Clarke, Notley, Macchi and Borghesi18].
However, the strength and spatial wavelength of such an isotropic and stochastic magnetic field still cannot be directly inferred from the experiments, as far as we are aware of. The reason for this is given below. The toroidal magnetic fields have an almost constant amplitude along the longitudinal direction; their transversal distribution, however, is two-dimensionally isotropic and stochastic[Reference Tzoufras, Ren, Tsung, Tonge, Mori, Fiore, Fonseca and Silva14]. When a probe proton passes through the plasma, the deflection distance is decided by the path integral of the stochastically distributed magnetic field, i.e.,
![]() $\int \boldsymbol{B}\,\text{d}l$
. The magnetic field vector is neutralized by itself during the integration. Instead of being able to extract the strength and spatial wavelength of the magnetic field, the striations on the detected proton images actually only help in giving the averaged result of the stochastic magnetic field vector along the path of the proton probe.
$\int \boldsymbol{B}\,\text{d}l$
. The magnetic field vector is neutralized by itself during the integration. Instead of being able to extract the strength and spatial wavelength of the magnetic field, the striations on the detected proton images actually only help in giving the averaged result of the stochastic magnetic field vector along the path of the proton probe.
In proton radiography of three-dimensionally isotropic and stochastic magnetic field turbulence, the mean strength and the main spatial wavelength of the magnetic turbulence can be inferred by extracting the energy spectrum of the magnetic energy
![]() $E_{B}(k)$
from the detected proton flux distribution[Reference Kugland, Ryutov, Plechaty, Ross and Park19–Reference Graziani, Tzeferacos, Lamb and Li21]. It has been verified by numerical demonstrations and used to evidence dynamo amplification of magnetic fields in a turbulent plasma[Reference Tzeferacos, Rigby, Bott, Bell, Bingham, Casner, Cattaneo, Churazov, Emig, Fiuza, Forest, Foster, Graziani, Katz, Koenig, Li, Meinecke, Petrasso, Park, Remington, Ross, Ryu, Ryutov, White, Reville, Miniati, Schekochihin, Lamb, Froula and Gregori22]. Nevertheless, this method, which requires three-dimensional isotropy, is not suitable for the detection of the Weibel-instability-generated magnetic field, since it is usually developed on the basis of anisotropy of the plasma[Reference Stockem, Dieckmann and Schlickeiser12].
$E_{B}(k)$
from the detected proton flux distribution[Reference Kugland, Ryutov, Plechaty, Ross and Park19–Reference Graziani, Tzeferacos, Lamb and Li21]. It has been verified by numerical demonstrations and used to evidence dynamo amplification of magnetic fields in a turbulent plasma[Reference Tzeferacos, Rigby, Bott, Bell, Bingham, Casner, Cattaneo, Churazov, Emig, Fiuza, Forest, Foster, Graziani, Katz, Koenig, Li, Meinecke, Petrasso, Park, Remington, Ross, Ryu, Ryutov, White, Reville, Miniati, Schekochihin, Lamb, Froula and Gregori22]. Nevertheless, this method, which requires three-dimensional isotropy, is not suitable for the detection of the Weibel-instability-generated magnetic field, since it is usually developed on the basis of anisotropy of the plasma[Reference Stockem, Dieckmann and Schlickeiser12].
In this paper, by theoretically analyzing proton radiography of a two-dimensionally isotropic and stochastic magnetic field, a relationship is built between the proton flux density perturbation on the detection plane and the energy spectrum of the magnetic field. We demonstrate for the first time that the mean strength and main spatial wavelength of the Weibel-instability-generated magnetic field can be inferred by means of proton radiography. Numerical calculations based on ray tracing methods are also conducted to verify our theory.
2 Proton radiography
The Weibel-instability-generated magnetic field has been investigated previously by many particle-in-cell simulations and experiments[Reference Fox, Fiksel, Bhattacharjee, Chang, Germaschewski, Hu and Nilson3–Reference Stockem, Grismayer, Fonseca and Silva13, Reference Kugland, Ryutov, Chang, Drake, Fikse, Froula, Glenzer, Gregori, Grosskopf, Koenig, Kuramitsu, Kuranz, Levy, Liang, Meinecke, Miniati, Morita, Pelka, Plechaty, Presura, Ravasio, Remington, Reville, Ross, Sakawa, Spitkovsky, Takabe and Park16–Reference Quinn, Romagnani, Ramakrishna, Sarri, Dieckmann, Wilson, Fuchs, Lancia, Pipah, Toncian, Willi, Clarke, Notley, Macchi and Borghesi18]. It is shown that when the Weibel instability is excited, current filaments emerge along the longitudinal direction, i.e., the
![]() $y$
direction in our coordinate system[Reference Fox, Fiksel, Bhattacharjee, Chang, Germaschewski, Hu and Nilson3]. The distribution of the center positions of these current filaments is two-dimensionally isotropic and stochastic in the transversal plane, i.e., the
$y$
direction in our coordinate system[Reference Fox, Fiksel, Bhattacharjee, Chang, Germaschewski, Hu and Nilson3]. The distribution of the center positions of these current filaments is two-dimensionally isotropic and stochastic in the transversal plane, i.e., the
![]() $x$
–
$x$
–
![]() $z$
plane. Magnetic fields are distributed around each current filament, and are azimuthally directed, i.e.,
$z$
plane. Magnetic fields are distributed around each current filament, and are azimuthally directed, i.e.,
![]() $\boldsymbol{B}=\boldsymbol{B}_{\unicode[STIX]{x1D711}}=\boldsymbol{B}_{x}+\boldsymbol{B}_{z}$
. The longitudinal component
$\boldsymbol{B}=\boldsymbol{B}_{\unicode[STIX]{x1D711}}=\boldsymbol{B}_{x}+\boldsymbol{B}_{z}$
. The longitudinal component
![]() $\boldsymbol{B}_{y}$
is small, and can be ignored. Compared to its transversal distribution, the magnetic field maintains a constant amplitude along the longitudinal direction, composing a tube-like structure around each current filament[Reference Sentoku, Mima, Kaw and Nishikawa8–Reference Stockem, Dieckmann and Schlickeiser12]. Because of the spatial distribution of the current filaments, the Weibel-instability-generated magnetic field is also two-dimensionally isotropic and stochastic[Reference Tzoufras, Ren, Tsung, Tonge, Mori, Fiore, Fonseca and Silva14]. Meanwhile, studies also show that after saturation of the Weibel instability, the magnetic field is quasi-static[Reference Karmakar, Kumar, Shvets, Polomarov and Pukhov23].
$\boldsymbol{B}_{y}$
is small, and can be ignored. Compared to its transversal distribution, the magnetic field maintains a constant amplitude along the longitudinal direction, composing a tube-like structure around each current filament[Reference Sentoku, Mima, Kaw and Nishikawa8–Reference Stockem, Dieckmann and Schlickeiser12]. Because of the spatial distribution of the current filaments, the Weibel-instability-generated magnetic field is also two-dimensionally isotropic and stochastic[Reference Tzoufras, Ren, Tsung, Tonge, Mori, Fiore, Fonseca and Silva14]. Meanwhile, studies also show that after saturation of the Weibel instability, the magnetic field is quasi-static[Reference Karmakar, Kumar, Shvets, Polomarov and Pukhov23].
In proton radiography of a magnetic field or an electric field, the proton probe will be deflected by the field and acquire a deflection velocity after it passes. The spatial distribution of the deflection velocity on exiting the field region is an important parameter. It creates a relationship between the proton flux density obtained on the detection plane and the field to be probed. Furthermore, it has also been proved to be helpful in field reconstruction from the proton flux density in previous studies[Reference Du and Wang24, Reference Zhang, Hua, Wan, Pai, Guo, Zhang, Ma, Li, Wu, Chu, Gu, Xu, Mori, Joshi, Wang and Lu25].
Assuming that the deflection distance of the proton probe inside the plasma is small and negligible, when a parallel proton beam has passed through the magnetic field region along the
![]() $z$
direction, the deflection velocity on exiting the field region can be approximated as
$z$
direction, the deflection velocity on exiting the field region can be approximated as
where
![]() $q$
is the proton charge,
$q$
is the proton charge,
![]() $m_{p}$
is the proton mass,
$m_{p}$
is the proton mass,
![]() $\unicode[STIX]{x1D6FE}$
is the proton relativistic factor and
$\unicode[STIX]{x1D6FE}$
is the proton relativistic factor and
![]() $l_{z}$
is the length of the magnetic field region in the
$l_{z}$
is the length of the magnetic field region in the
![]() $z$
direction. Actually, as well as the emergence of
$z$
direction. Actually, as well as the emergence of
![]() $u_{y}$
, which comes from the coupling between
$u_{y}$
, which comes from the coupling between
![]() $B_{x}$
and
$B_{x}$
and
![]() $u_{z}$
, a deflection velocity in the
$u_{z}$
, a deflection velocity in the
![]() $x$
direction,
$x$
direction,
![]() $u_{x}$
, can also arise due to the coupling between
$u_{x}$
, can also arise due to the coupling between
![]() $u_{y}$
and
$u_{y}$
and
![]() $B_{z}$
. It is later proved by the numerical calculations in Section 4 that
$B_{z}$
. It is later proved by the numerical calculations in Section 4 that
![]() $u_{x}$
is several orders of magnitude lower than
$u_{x}$
is several orders of magnitude lower than
![]() $u_{y}$
, and is ignored in our analyses.
$u_{y}$
, and is ignored in our analyses.
After leaving the field region and traversing a distance
![]() $L_{D}$
in free space, the proton probe will be deposited on the detection plane. The spatial distribution of the deflection velocity finally introduces a perturbation to the spatial density distribution of the proton probe, which will become visible on the detection plane if
$L_{D}$
in free space, the proton probe will be deposited on the detection plane. The spatial distribution of the deflection velocity finally introduces a perturbation to the spatial density distribution of the proton probe, which will become visible on the detection plane if
![]() $L_{D}$
is large enough. The density perturbation is defined as
$L_{D}$
is large enough. The density perturbation is defined as
![]() $\unicode[STIX]{x1D6FF}n/n_{0}=n/n_{0}-1$
, where
$\unicode[STIX]{x1D6FF}n/n_{0}=n/n_{0}-1$
, where
![]() $n$
and
$n$
and
![]() $n_{0}$
are the proton flux densities on the detection plane when the magnetic field is present and absent, respectively. When the density perturbation satisfies the linear requirement
$n_{0}$
are the proton flux densities on the detection plane when the magnetic field is present and absent, respectively. When the density perturbation satisfies the linear requirement
![]() $\unicode[STIX]{x1D6FF}n/n_{0}<1$
, the trajectory crossing or overlapping between the protons would not happen under the chosen spatial resolution. The linearized continuity equation
$\unicode[STIX]{x1D6FF}n/n_{0}<1$
, the trajectory crossing or overlapping between the protons would not happen under the chosen spatial resolution. The linearized continuity equation
![]() $\unicode[STIX]{x1D6FF}n/n_{0}=-\unicode[STIX]{x2202}d/\unicode[STIX]{x2202}y$
is then satisfied, where
$\unicode[STIX]{x1D6FF}n/n_{0}=-\unicode[STIX]{x2202}d/\unicode[STIX]{x2202}y$
is then satisfied, where
![]() $d$
is the deflection distance in free space[Reference Du and Wang24]. Because
$d$
is the deflection distance in free space[Reference Du and Wang24]. Because
![]() $d/L_{D}=u_{y}/u_{z}$
, the deflection velocity on exiting the field region then can be reconstructed from
$d/L_{D}=u_{y}/u_{z}$
, the deflection velocity on exiting the field region then can be reconstructed from
where
![]() $u_{z}$
is the initial velocity of the proton in the
$u_{z}$
is the initial velocity of the proton in the
![]() $z$
direction and
$z$
direction and
![]() $y_{0}$
is the spatial boundary of
$y_{0}$
is the spatial boundary of
![]() $\unicode[STIX]{x1D6FF}n/n_{0}$
along the
$\unicode[STIX]{x1D6FF}n/n_{0}$
along the
![]() $y$
direction on the detection plane.
$y$
direction on the detection plane.
It is necessary to mention that the impact of the electric field on the probe proton, which is mainly due to the space charge effect between the current filaments, has been experimentally proved to be negligible when compared with that of the magnetic field[Reference Huntington, Fiuza, Ross, Zylstra, Drake, Froula, Gregori, Kugland, Kuranz, Levy, Li, Meinecke, Morita, Petrasso, Plechaty, Remington, Ryutov, Sakawa, Spitkovsky, Takabe and Park17, Reference Quinn, Romagnani, Ramakrishna, Sarri, Dieckmann, Wilson, Fuchs, Lancia, Pipah, Toncian, Willi, Clarke, Notley, Macchi and Borghesi18]. In this paper, the influence of the electric field is also not taken into consideration.
3 Energy spectrum of the magnetic field and deflection velocity
In fluid physics, the velocity autocorrelation tensor is a commonly used tool to deduce the energy spectrum of three-dimensional fluid turbulence[Reference Davidson26]. In analyzing three-dimensionally isotropic and stochastic magnetic turbulence, the autocorrelation tensor of the turbulent magnetic field is also useful in obtaining the energy spectrum of the magnetic field[Reference Bott, Graziani, Tzeferacos, White, Lamb, Gregori and Schekochihin20]. In this paper, the autocorrelation tensor of the two-dimensionally isotropic, stochastic and static magnetic field
![]() $\boldsymbol{B}$
is defined as
$\boldsymbol{B}$
is defined as
where the subscripts
![]() $i$
and
$i$
and
![]() $j$
stand for
$j$
stand for
![]() $x$
or
$x$
or
![]() $z$
,
$z$
,
![]() $\boldsymbol{p}$
and
$\boldsymbol{p}$
and
![]() $\boldsymbol{p}^{\prime }$
are two arbitrary positions on the
$\boldsymbol{p}^{\prime }$
are two arbitrary positions on the
![]() $x$
–
$x$
–
![]() $z$
plane, and the bracket
$z$
plane, and the bracket
![]() $\langle ~\rangle$
stands for the mean operator. Because of the isotropy of the magnetic field in the
$\langle ~\rangle$
stands for the mean operator. Because of the isotropy of the magnetic field in the
![]() $x$
–
$x$
–
![]() $z$
plane,
$z$
plane,
![]() $R_{ij}(\boldsymbol{p},\boldsymbol{p}^{\prime })$
can be written as a function of the displacement vector
$R_{ij}(\boldsymbol{p},\boldsymbol{p}^{\prime })$
can be written as a function of the displacement vector
![]() $\boldsymbol{r}=\boldsymbol{p}-\boldsymbol{p}^{\prime }=r_{x}\boldsymbol{e}_{x}+r_{z}\boldsymbol{e}_{z}$
using
$\boldsymbol{r}=\boldsymbol{p}-\boldsymbol{p}^{\prime }=r_{x}\boldsymbol{e}_{x}+r_{z}\boldsymbol{e}_{z}$
using
![]() $R_{ij}(\boldsymbol{r})$
. The two-dimensional Fourier transform of
$R_{ij}(\boldsymbol{r})$
. The two-dimensional Fourier transform of
![]() $R_{ij}(\boldsymbol{r})$
is
$R_{ij}(\boldsymbol{r})$
is
where
![]() $\boldsymbol{k}=k_{x}\boldsymbol{e}_{x}+k_{z}\boldsymbol{e}_{z}$
. The inverse Fourier transform of
$\boldsymbol{k}=k_{x}\boldsymbol{e}_{x}+k_{z}\boldsymbol{e}_{z}$
. The inverse Fourier transform of
![]() $\hat{R}_{ij}(\boldsymbol{k})$
is
$\hat{R}_{ij}(\boldsymbol{k})$
is
Defining an autocorrelation function
![]() $R(\boldsymbol{r})$
with the trace of the autocorrelation tensor,
$R(\boldsymbol{r})$
with the trace of the autocorrelation tensor,
In this paper, the subscript
![]() $ii$
means that the Einstein summation convention is used. Because of the isotropy,
$ii$
means that the Einstein summation convention is used. Because of the isotropy,
![]() $R_{xx}(\boldsymbol{r})=R(\boldsymbol{r})/2$
. Clearly, when
$R_{xx}(\boldsymbol{r})=R(\boldsymbol{r})/2$
. Clearly, when
![]() $\boldsymbol{r}=0$
,
$\boldsymbol{r}=0$
,
![]() $R(\boldsymbol{r}=0)$
actually stands for the mean energy of the magnetic field, i.e.,
$R(\boldsymbol{r}=0)$
actually stands for the mean energy of the magnetic field, i.e.,
![]() $B_{\text{rms}}^{2}=\langle |\boldsymbol{B}_{x}|^{2}+|\boldsymbol{B}_{y}|^{2}\rangle$
. The subscript rms is an abbreviation for root mean square. Substituting Equation (5) into Equation (6) and letting
$B_{\text{rms}}^{2}=\langle |\boldsymbol{B}_{x}|^{2}+|\boldsymbol{B}_{y}|^{2}\rangle$
. The subscript rms is an abbreviation for root mean square. Substituting Equation (5) into Equation (6) and letting
![]() $\boldsymbol{r}=0$
yields
$\boldsymbol{r}=0$
yields
where
![]() $\unicode[STIX]{x1D711}$
is the polar angle in the
$\unicode[STIX]{x1D711}$
is the polar angle in the
![]() $\boldsymbol{k}$
plane. Under the assumption of two-dimensional isotropy, Equation (7) can be rewritten as
$\boldsymbol{k}$
plane. Under the assumption of two-dimensional isotropy, Equation (7) can be rewritten as
Considering that
![]() $R(\boldsymbol{r}=0)$
corresponds to the magnetic field energy, the integrand
$R(\boldsymbol{r}=0)$
corresponds to the magnetic field energy, the integrand
![]() $2\unicode[STIX]{x1D70B}k\hat{R}(k)$
actually is the energy spectrum of the magnetic field, and is denoted by
$2\unicode[STIX]{x1D70B}k\hat{R}(k)$
actually is the energy spectrum of the magnetic field, and is denoted by
where
![]() $\hat{R}(k)=\hat{R}_{ii}(k)$
. Letting
$\hat{R}(k)=\hat{R}_{ii}(k)$
. Letting
![]() $k=k_{x}$
and
$k=k_{x}$
and
![]() $k_{z}=0$
, we have
$k_{z}=0$
, we have
Similar to the definition of
![]() $R_{ij}(\boldsymbol{p},\boldsymbol{p}^{\prime })$
, the autocorrelation tensor of the deflection velocity
$R_{ij}(\boldsymbol{p},\boldsymbol{p}^{\prime })$
, the autocorrelation tensor of the deflection velocity
![]() $\boldsymbol{u}$
is defined as
$\boldsymbol{u}$
is defined as
Substituting Equation (1) into Equation (11) gives
Letting
![]() $r_{z}=z-z^{\prime }$
, we get
$r_{z}=z-z^{\prime }$
, we get
Because at the outside region of the magnetic field,
![]() $R_{xx}(\boldsymbol{r})\approx 0$
, the upper and lower integral limits in Equation (13) can be extended to
$R_{xx}(\boldsymbol{r})\approx 0$
, the upper and lower integral limits in Equation (13) can be extended to
![]() $(-\infty ,\infty )$
approximately. After substituting
$(-\infty ,\infty )$
approximately. After substituting
![]() $R_{xx}(\boldsymbol{r})=R(\boldsymbol{r})/2$
into Equation (13), we have
$R_{xx}(\boldsymbol{r})=R(\boldsymbol{r})/2$
into Equation (13), we have
Equation (14) builds a relationship between the autocorrelation tensors of the two-dimensional magnetic field and the one-dimensional deflection velocity. The one-dimensional Fourier transforms of the left- and right-hand sides of Equation (14) give
and
where Equation (16) has been written as a two-dimensional Fourier transform form of
![]() $R(r_{x},r_{z})$
by letting
$R(r_{x},r_{z})$
by letting
![]() $k_{z}=0$
. By rewriting
$k_{z}=0$
. By rewriting
![]() $\hat{M}_{yy}(k_{x})$
as
$\hat{M}_{yy}(k_{x})$
as
![]() $E_{u}(k_{x})$
, we get
$E_{u}(k_{x})$
, we get
The inverse Fourier transform of
![]() $\hat{M}_{yy}(k_{x})$
has the form
$\hat{M}_{yy}(k_{x})$
has the form
At the same time, according to Parseval’s theorem in the one-dimensional case, it gives that
where
![]() $\hat{u} _{y}(k_{x})=(1/2\unicode[STIX]{x1D70B})\int u_{y}(x)e^{-ik_{x}x}\,\text{d}x$
.
$\hat{u} _{y}(k_{x})=(1/2\unicode[STIX]{x1D70B})\int u_{y}(x)e^{-ik_{x}x}\,\text{d}x$
.
From
![]() $M_{yy}(r_{x})=\langle \boldsymbol{u}_{y}(x)\boldsymbol{u}_{y}(x+r_{x})\rangle$
we know that, if
$M_{yy}(r_{x})=\langle \boldsymbol{u}_{y}(x)\boldsymbol{u}_{y}(x+r_{x})\rangle$
we know that, if
![]() $r_{x}=0$
,
$r_{x}=0$
,
![]() $M_{yy}(r_{x}=0)=\langle u_{y}^{2}(x)\rangle$
. Thus, by letting
$M_{yy}(r_{x}=0)=\langle u_{y}^{2}(x)\rangle$
. Thus, by letting
![]() $r_{x}=0$
and substituting Equation (18) into Equation (19), we obtain
$r_{x}=0$
and substituting Equation (18) into Equation (19), we obtain
Clearly,
![]() $\hat{M}_{yy}(k_{x})=(2\unicode[STIX]{x1D70B}/l_{x})\hat{u} _{y}^{2}(k_{x})$
. Then, the energy spectrum of the deflection velocity is deduced as
$\hat{M}_{yy}(k_{x})=(2\unicode[STIX]{x1D70B}/l_{x})\hat{u} _{y}^{2}(k_{x})$
. Then, the energy spectrum of the deflection velocity is deduced as
4 Strength and wavelength of the magnetic field
By combining Equations (10), (17) and (21), we get
which means that a relationship is built between the energy spectrum of the magnetic field and the spatial spectrum of the deflection velocity. When the spatial distribution of the one-dimensional deflection velocity
![]() $u_{y}(x)$
is obtained, the energy spectrum of the two-dimensionally isotropic and stochastic magnetic field can then be deduced. The method of obtaining
$u_{y}(x)$
is obtained, the energy spectrum of the two-dimensionally isotropic and stochastic magnetic field can then be deduced. The method of obtaining
![]() $u_{y}(x)$
from proton radiography has been presentedin Section 3.
$u_{y}(x)$
from proton radiography has been presentedin Section 3.
The mean strength of the magnetic field is then acquired through
The main spatial wavelength of
![]() $|\boldsymbol{B}|^{2}$
, i.e.,
$|\boldsymbol{B}|^{2}$
, i.e.,
![]() $\unicode[STIX]{x1D706}_{|B|^{2}}=2\unicode[STIX]{x1D70B}/k_{x}$
, can be read from the energy spectrum of the stochastic magnetic field
$\unicode[STIX]{x1D706}_{|B|^{2}}=2\unicode[STIX]{x1D70B}/k_{x}$
, can be read from the energy spectrum of the stochastic magnetic field
![]() $E_{B}(k_{x})$
. The main spatial wavelength of the magnetic field
$E_{B}(k_{x})$
. The main spatial wavelength of the magnetic field
![]() $|\boldsymbol{B}|$
then equals
$|\boldsymbol{B}|$
then equals
5 Numerical verification
In order to validate the above theory, numerical calculations based on ray tracing methods are conducted to simulate radiography of the Weibel-instability-generated two-dimensionally isotropic and stochastic magnetic field[Reference Du and Wang24].

Figure 1. Schematic diagram of proton radiography of a two-dimensionally isotropic and stochastic magnetic field.
The three-dimensional magnetic field to be radiographed is pre-set as follows. Two hundred tube-like magnetic field structures are distributed in a cross-section of
![]() $l_{x}\times l_{z}=0.8~\text{mm}\times 0.8~\text{mm}$
in the
$l_{x}\times l_{z}=0.8~\text{mm}\times 0.8~\text{mm}$
in the
![]() $x$
–
$x$
–
![]() $z$
plane, with the current filaments directed along the
$z$
plane, with the current filaments directed along the
![]() $y$
direction, as shown in Figure 1. The field region in the
$y$
direction, as shown in Figure 1. The field region in the
![]() $y$
direction is from
$y$
direction is from
![]() $y=0~\text{mm}$
to
$y=0~\text{mm}$
to
![]() $y=4~\text{mm}$
. According to the Biot–Savart law, the spatial distribution of each magnetic tube can be expressed as
$y=4~\text{mm}$
. According to the Biot–Savart law, the spatial distribution of each magnetic tube can be expressed as
![]() $\boldsymbol{B}_{p}=[B_{0}(r-r_{0})/R_{0}]\exp [-(r-r_{0})^{2}/R_{0}^{2}]\exp (-y^{2}/l_{y}^{2})\boldsymbol{e}_{\unicode[STIX]{x1D711}}$
, where
$\boldsymbol{B}_{p}=[B_{0}(r-r_{0})/R_{0}]\exp [-(r-r_{0})^{2}/R_{0}^{2}]\exp (-y^{2}/l_{y}^{2})\boldsymbol{e}_{\unicode[STIX]{x1D711}}$
, where
![]() $r=\sqrt{x^{2}+z^{2}}$
,
$r=\sqrt{x^{2}+z^{2}}$
,
![]() $\boldsymbol{e}_{\unicode[STIX]{x1D711}}=\boldsymbol{e}_{x}+\boldsymbol{e}_{y}$
, and
$\boldsymbol{e}_{\unicode[STIX]{x1D711}}=\boldsymbol{e}_{x}+\boldsymbol{e}_{y}$
, and
![]() $R_{0}$
and
$R_{0}$
and
![]() $l_{y}$
denote the transversal and longitudinal lengths of the tube, respectively. The subscript
$l_{y}$
denote the transversal and longitudinal lengths of the tube, respectively. The subscript
![]() $p$
is an abbreviation for pre-set.
$p$
is an abbreviation for pre-set.
![]() $B_{0}$
is the amplitude of the magnetic field tube and
$B_{0}$
is the amplitude of the magnetic field tube and
![]() $r_{0}$
is the transversal center position of each magnetic tube. For each magnetic tube,
$r_{0}$
is the transversal center position of each magnetic tube. For each magnetic tube,
![]() $r_{0}$
is randomly distributed in the transversal plane. According to previous experiments and the particle-in-cell simulations,
$r_{0}$
is randomly distributed in the transversal plane. According to previous experiments and the particle-in-cell simulations,
![]() $B_{0}$
and
$B_{0}$
and
![]() $R_{0}$
are set to be 10 T and
$R_{0}$
are set to be 10 T and
![]() $40~\unicode[STIX]{x03BC}\text{m}$
, respectively[Reference Quinn, Romagnani, Ramakrishna, Sarri, Dieckmann, Wilson, Fuchs, Lancia, Pipah, Toncian, Willi, Clarke, Notley, Macchi and Borghesi18].
$40~\unicode[STIX]{x03BC}\text{m}$
, respectively[Reference Quinn, Romagnani, Ramakrishna, Sarri, Dieckmann, Wilson, Fuchs, Lancia, Pipah, Toncian, Willi, Clarke, Notley, Macchi and Borghesi18].
![]() $l_{y}$
is set to be 1.2 mm, which is long enough when compared to the transversal length of the magnetic tube. It allows us to regard the magnetic tube as being constantly distributed in the longitudinal direction, which, most importantly, suggests that the isotropy of the pre-set magnetic field is two-dimensional. These parameter settings correspond to the situation of a thermal anisotropy-driven Weibel instability during the process of plasma expanding into the vacuum[Reference Quinn, Romagnani, Ramakrishna, Sarri, Dieckmann, Wilson, Fuchs, Lancia, Pipah, Toncian, Willi, Clarke, Notley, Macchi and Borghesi18].
$l_{y}$
is set to be 1.2 mm, which is long enough when compared to the transversal length of the magnetic tube. It allows us to regard the magnetic tube as being constantly distributed in the longitudinal direction, which, most importantly, suggests that the isotropy of the pre-set magnetic field is two-dimensional. These parameter settings correspond to the situation of a thermal anisotropy-driven Weibel instability during the process of plasma expanding into the vacuum[Reference Quinn, Romagnani, Ramakrishna, Sarri, Dieckmann, Wilson, Fuchs, Lancia, Pipah, Toncian, Willi, Clarke, Notley, Macchi and Borghesi18].

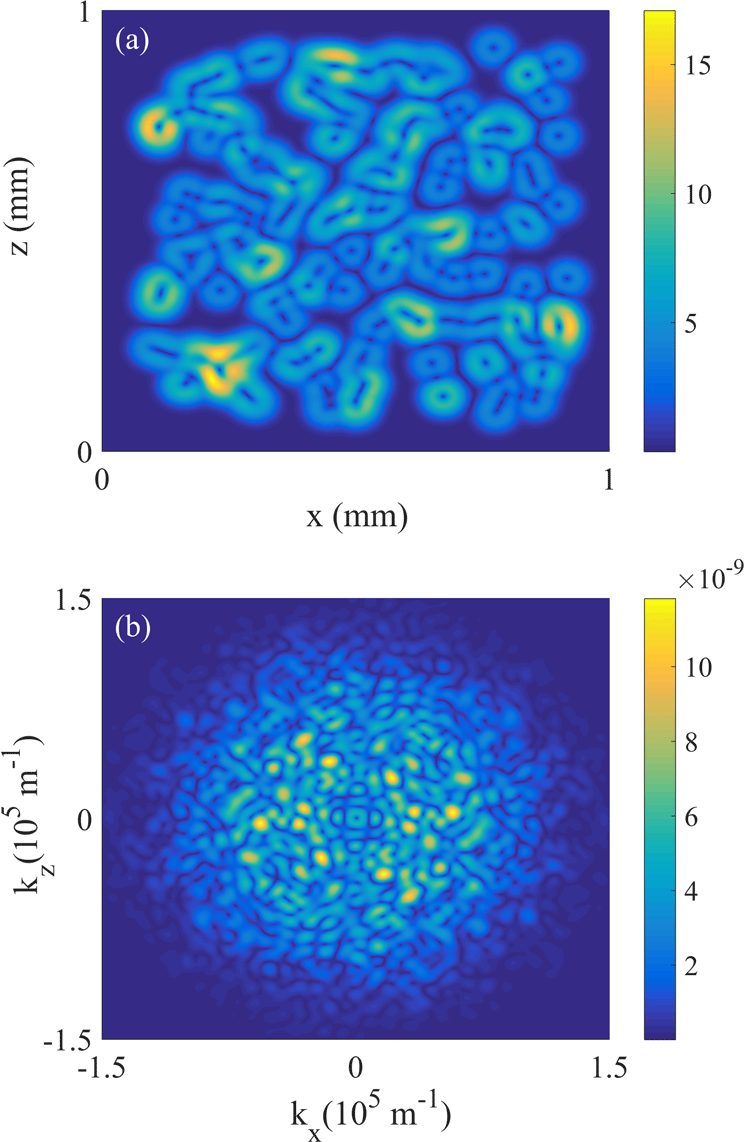
Figure 2. (a) Transversal cross-section of the pre-set stochastic magnetic field tubes at
![]() $y=2~\text{mm}$
. (b) Two-dimensional spectrum of the magnetic field by taking Fourier transforms of the field in (a), which shows an isotropic feature.
$y=2~\text{mm}$
. (b) Two-dimensional spectrum of the magnetic field by taking Fourier transforms of the field in (a), which shows an isotropic feature.
The cross-section of the magnetic field strength at
![]() $y=2~\text{mm}$
is shown in Figure 2(a). The maximum strength is about 17 T. This is greater than
$y=2~\text{mm}$
is shown in Figure 2(a). The maximum strength is about 17 T. This is greater than
![]() $B_{0}$
, which results from the spatial overlap of the magnetic tubes. In Figure 2(b), the two-dimensional distribution of the magnetic field in
$B_{0}$
, which results from the spatial overlap of the magnetic tubes. In Figure 2(b), the two-dimensional distribution of the magnetic field in
![]() $\boldsymbol{k}$
space
$\boldsymbol{k}$
space
![]() $\hat{B}_{p}(k_{x},k_{z})=\sqrt{|\hat{\boldsymbol{B}}_{xp}(k_{x},k_{z})|^{2}+|\hat{\boldsymbol{B}}_{zp}(k_{x},k_{z})|^{2}}$
suggests that the magnetic field is approximately isotropic in the
$\hat{B}_{p}(k_{x},k_{z})=\sqrt{|\hat{\boldsymbol{B}}_{xp}(k_{x},k_{z})|^{2}+|\hat{\boldsymbol{B}}_{zp}(k_{x},k_{z})|^{2}}$
suggests that the magnetic field is approximately isotropic in the
![]() $x$
–
$x$
–
![]() $z$
plane, where
$z$
plane, where
![]() $\hat{\boldsymbol{B}}_{xp}(k_{x},k_{z})$
and
$\hat{\boldsymbol{B}}_{xp}(k_{x},k_{z})$
and
![]() $\hat{\boldsymbol{B}}_{zp}(k_{x},k_{z})$
are the two-dimensional Fourier transforms of
$\hat{\boldsymbol{B}}_{zp}(k_{x},k_{z})$
are the two-dimensional Fourier transforms of
![]() $\boldsymbol{B}_{xp}(x,z)$
and
$\boldsymbol{B}_{xp}(x,z)$
and
![]() $\boldsymbol{B}_{zp}(x,z)$
, respectively. The mean strength of the pre-set magnetic field
$\boldsymbol{B}_{zp}(x,z)$
, respectively. The mean strength of the pre-set magnetic field
![]() $B_{\text{rmsp}}$
can be acquired conveniently by making a spatial average of the magnetic field distribution
$B_{\text{rmsp}}$
can be acquired conveniently by making a spatial average of the magnetic field distribution
![]() $B_{p}(x,z)=\sqrt{|\boldsymbol{B}_{xp}(x,z)|^{2}+|\boldsymbol{B}_{zp}(x,z)|^{2}}$
in the
$B_{p}(x,z)=\sqrt{|\boldsymbol{B}_{xp}(x,z)|^{2}+|\boldsymbol{B}_{zp}(x,z)|^{2}}$
in the
![]() $x$
–
$x$
–
![]() $z$
plane, i.e.,
$z$
plane, i.e.,
![]() $B_{\text{rmsp}}=(1/S)\iint B_{p}(x,z)\,\text{d}x\text{d}z$
, where
$B_{\text{rmsp}}=(1/S)\iint B_{p}(x,z)\,\text{d}x\text{d}z$
, where
![]() $S$
is the transversal cross-sectional area of the magnetic field region. It is inferred from Figure 2(a) that
$S$
is the transversal cross-sectional area of the magnetic field region. It is inferred from Figure 2(a) that
![]() $B_{\text{rmsp}}\approx 4.51~\text{T}$
.
$B_{\text{rmsp}}\approx 4.51~\text{T}$
.
The energy spectrum of the pre-set magnetic field in Figure 2(a),
![]() $E_{Bp}(k_{x})$
, can be acquired as follows. From the two-dimensional Parseval’s theorem
$E_{Bp}(k_{x})$
, can be acquired as follows. From the two-dimensional Parseval’s theorem
we know that
![]() $B_{\text{rmsp}}^{2}=\int (8\unicode[STIX]{x1D70B}^{3}/S)k|\hat{B}_{p}(k)|^{2}\,\text{d}k$
, where
$B_{\text{rmsp}}^{2}=\int (8\unicode[STIX]{x1D70B}^{3}/S)k|\hat{B}_{p}(k)|^{2}\,\text{d}k$
, where
![]() $\hat{B}_{p}(k)$
is the one-dimensional spectrum of the magnetic field in
$\hat{B}_{p}(k)$
is the one-dimensional spectrum of the magnetic field in
![]() $k=\sqrt{k_{x}^{2}+k_{z}^{2}}$
space and can be deduced from
$k=\sqrt{k_{x}^{2}+k_{z}^{2}}$
space and can be deduced from
![]() $\hat{B}_{p}(k_{x},k_{z})$
in Figure 2(b). According to Equation (9), the one-dimensional energy spectrum of the pre-set magnetic field is then given as
$\hat{B}_{p}(k_{x},k_{z})$
in Figure 2(b). According to Equation (9), the one-dimensional energy spectrum of the pre-set magnetic field is then given as
![]() $E_{Bp}(k)=(8\unicode[STIX]{x1D70B}^{3}/S)k|\hat{B}_{p}(k)|^{2}$
, shown as the red line in Figure 3. The blue line corresponds to the energy spectrum of the magnetic field extracted from the proton radiography, which will be described in detail later. Because of the isotropy,
$E_{Bp}(k)=(8\unicode[STIX]{x1D70B}^{3}/S)k|\hat{B}_{p}(k)|^{2}$
, shown as the red line in Figure 3. The blue line corresponds to the energy spectrum of the magnetic field extracted from the proton radiography, which will be described in detail later. Because of the isotropy,
![]() $E_{Bp}(k_{x})=E_{Bp}(k)$
. The mean strength of the pre-set magnetic field, when deduced from
$E_{Bp}(k_{x})=E_{Bp}(k)$
. The mean strength of the pre-set magnetic field, when deduced from
![]() $E_{Bp}(k_{x})$
by
$E_{Bp}(k_{x})$
by
![]() $B_{\text{rmsp}}=\sqrt{\int _{0}^{\infty }\,\text{d}kE_{Bp}(k_{x})}$
, is found to be
$B_{\text{rmsp}}=\sqrt{\int _{0}^{\infty }\,\text{d}kE_{Bp}(k_{x})}$
, is found to be
![]() $B_{\text{rmsp}}\approx 4.51~\text{T}$
, which is equal to the result obtained from the spatial averaging method previously. At the same time, the main wavelength of the pre-set magnetic field, which is taken from the highest peak on the energy spectrum of the pre-set magnetic field in Figure 3, is about
$B_{\text{rmsp}}\approx 4.51~\text{T}$
, which is equal to the result obtained from the spatial averaging method previously. At the same time, the main wavelength of the pre-set magnetic field, which is taken from the highest peak on the energy spectrum of the pre-set magnetic field in Figure 3, is about
![]() $\unicode[STIX]{x1D706}_{|B|p}=\unicode[STIX]{x1D706}_{|B|^{2}p}\approx 86~\unicode[STIX]{x03BC}\text{m}$
.
$\unicode[STIX]{x1D706}_{|B|p}=\unicode[STIX]{x1D706}_{|B|^{2}p}\approx 86~\unicode[STIX]{x03BC}\text{m}$
.

Figure 3. One-dimensional energy spectrum of the magnetic field
![]() $E_{B}(k)$
. The red line corresponds to the energy spectrum obtained by taking Fourier transforms of the pre-set magnetic field in Figure 2(a), whereas the blue line corresponds to the energy spectrum extracted from proton radiography with Equation (22).
$E_{B}(k)$
. The red line corresponds to the energy spectrum obtained by taking Fourier transforms of the pre-set magnetic field in Figure 2(a), whereas the blue line corresponds to the energy spectrum extracted from proton radiography with Equation (22).
In this paper, our interest is limited to the case in which the Weibel instability is collisionless. In proton radiography of the Weibel-instability-generated magnetic field, the spatial density perturbation of the proton beam, which is introduced from the magnetic field, is small enough to avoid the probe trajectory crossing or overlapping. Also, space charge effects between the probe protons are neglected. This allows the ray tracing method to be used to simulate the process of proton radiography of the magnetic field. In this paper, the kinetic energy of the mono-energy probe proton is 10 MeV, emitted parallel with the
![]() $z$
direction from an extended proton source. The distance from the detection plane to the magnetic field region is
$z$
direction from an extended proton source. The distance from the detection plane to the magnetic field region is
![]() $L_{D}=5~\text{cm}$
. The trajectories of the probe protons inside the field region are calculated with the Runge–Kutta algorithm. Outside of the field region, the probe protons drift during free flight before they reach the detection plane.
$L_{D}=5~\text{cm}$
. The trajectories of the probe protons inside the field region are calculated with the Runge–Kutta algorithm. Outside of the field region, the probe protons drift during free flight before they reach the detection plane.
Numerical results show that after traversing the field region, the maximum proton deflection velocity in the
![]() $y$
direction,
$y$
direction,
![]() $u_{y\text{max}}$
, is about
$u_{y\text{max}}$
, is about
![]() $2.1\times 10^{5}~\text{m}/\text{s}$
. While in the
$2.1\times 10^{5}~\text{m}/\text{s}$
. While in the
![]() $x$
direction, the maximum deflection velocity,
$x$
direction, the maximum deflection velocity,
![]() $u_{x\text{max}}$
, is about
$u_{x\text{max}}$
, is about
![]() $1.5\times 10^{2}~\text{m}/\text{s}$
, which is about three orders of magnitude lower than
$1.5\times 10^{2}~\text{m}/\text{s}$
, which is about three orders of magnitude lower than
![]() $u_{y\text{max}}$
. This ensures the assumption of
$u_{y\text{max}}$
. This ensures the assumption of
![]() $\boldsymbol{u}\approx u_{y}\boldsymbol{e}_{y}$
in Equation (1). It also indicates that in proton radiography of a Weibel-instability-generated magnetic field, the proton density striations on the detection plane are mainly contributed by the longitudinal deflection velocity
$\boldsymbol{u}\approx u_{y}\boldsymbol{e}_{y}$
in Equation (1). It also indicates that in proton radiography of a Weibel-instability-generated magnetic field, the proton density striations on the detection plane are mainly contributed by the longitudinal deflection velocity
![]() $u_{y}$
, and the influence introduced to proton radiography by
$u_{y}$
, and the influence introduced to proton radiography by
![]() $B_{z}$
is negligible.
$B_{z}$
is negligible.
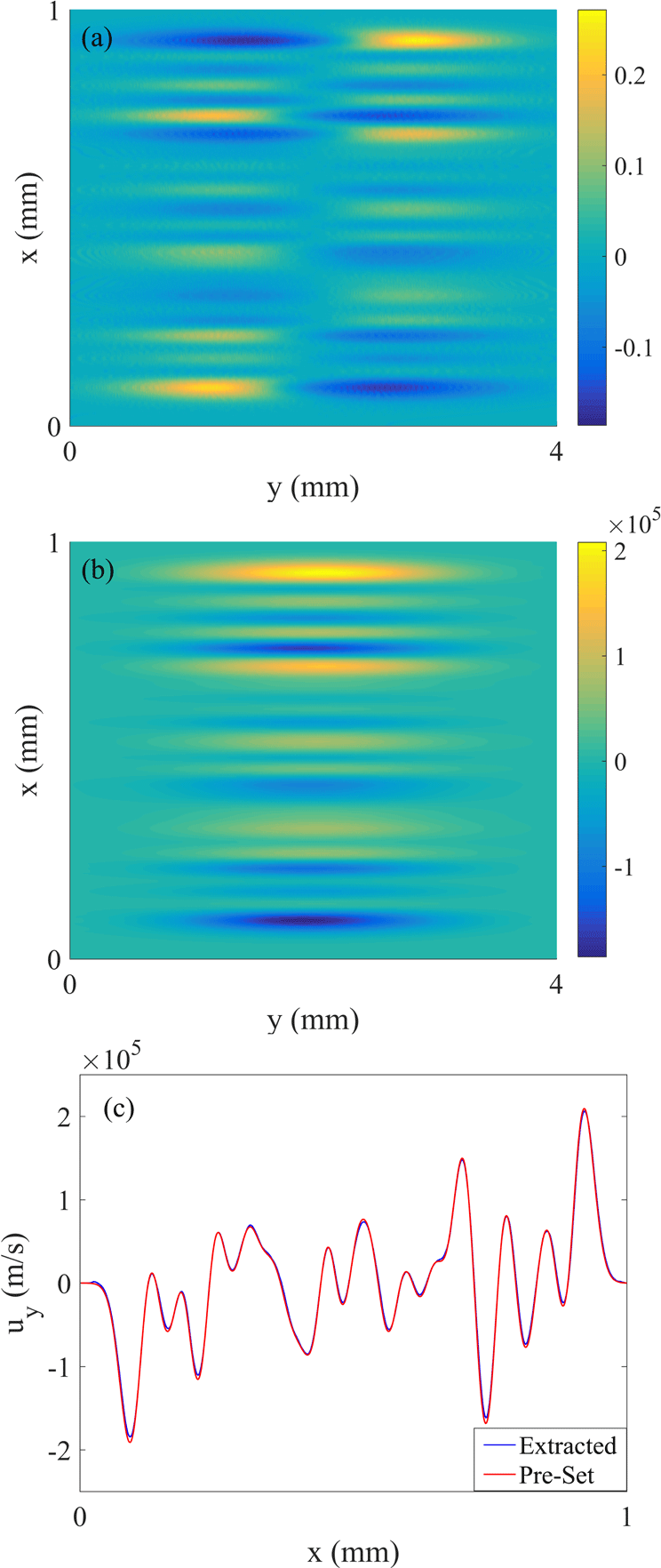
Figure 4(a) shows the proton density perturbation on the detection plane. The spatial structures in Figure 4(a) are quite similar to the results in Figure 2 of the publication by Huntington et al., which are obtained with both particle-in-cell simulations and experiments[Reference Huntington, Fiuza, Ross, Zylstra, Drake, Froula, Gregori, Kugland, Kuranz, Levy, Li, Meinecke, Morita, Petrasso, Plechaty, Remington, Ryutov, Sakawa, Spitkovsky, Takabe and Park17]. This also helps to support the model simplification in our paper.

Figure 4. (a) Proton density perturbation
![]() $\unicode[STIX]{x1D6FF}n/n_{0}$
on the detection plane when
$\unicode[STIX]{x1D6FF}n/n_{0}$
on the detection plane when
![]() $L_{D}=5~\text{cm}$
. (b) The extracted two-dimensional distribution of
$L_{D}=5~\text{cm}$
. (b) The extracted two-dimensional distribution of
![]() $u_{y}$
. (c) One-dimensional distributions of
$u_{y}$
. (c) One-dimensional distributions of
![]() $u_{y}$
at
$u_{y}$
at
![]() $y=2~\text{mm}$
from the extracted results and the pre-settings.
$y=2~\text{mm}$
from the extracted results and the pre-settings.
From Figure 4(a) we can see that
![]() $\unicode[STIX]{x1D6FF}n/n_{0}<1$
, which indicates that the linearity requirement is satisfied and trajectory crossings or overlappings between the protons do not happen under our chosen spatial resolution[Reference Du and Wang24]. It allows us to reconstruct the deflection velocity at the exit of the field region from the density perturbation in Figure 4(a) with Equation (2). The spatial distribution of the reconstructed deflection velocity
$\unicode[STIX]{x1D6FF}n/n_{0}<1$
, which indicates that the linearity requirement is satisfied and trajectory crossings or overlappings between the protons do not happen under our chosen spatial resolution[Reference Du and Wang24]. It allows us to reconstruct the deflection velocity at the exit of the field region from the density perturbation in Figure 4(a) with Equation (2). The spatial distribution of the reconstructed deflection velocity
![]() $u_{ye}$
is shown in Figure 4(b). The one-dimensional distribution of the extracted
$u_{ye}$
is shown in Figure 4(b). The one-dimensional distribution of the extracted
![]() $u_{ye}$
at
$u_{ye}$
at
![]() $y=2~\text{mm}$
is shown as the blue line in Figure 4(c), which is almost coincident with the deflection velocity integrated from Equation (1) with the pre-set magnetic field, shown as the red line in Figure 4(c). In order to distinguish them from the pre-set values of the magnetic field, the results extracted from the proton density perturbation are all subscripted with
$y=2~\text{mm}$
is shown as the blue line in Figure 4(c), which is almost coincident with the deflection velocity integrated from Equation (1) with the pre-set magnetic field, shown as the red line in Figure 4(c). In order to distinguish them from the pre-set values of the magnetic field, the results extracted from the proton density perturbation are all subscripted with
![]() $e$
as an abbreviation for extracted. The perfect agreement between the two deflection velocities is due to two reasons. Firstly, the low-density perturbation in Figure 4(a) indicates that the trajectory crossings of the probe protons are sufficiently prevented under the chosen spatial resolution. Secondly, the density perturbation is almost invisible at the exit of the field region (not shown), i.e.,
$e$
as an abbreviation for extracted. The perfect agreement between the two deflection velocities is due to two reasons. Firstly, the low-density perturbation in Figure 4(a) indicates that the trajectory crossings of the probe protons are sufficiently prevented under the chosen spatial resolution. Secondly, the density perturbation is almost invisible at the exit of the field region (not shown), i.e.,
![]() $\unicode[STIX]{x1D6FF}n/n_{0}\approx 0$
. This indicates that the deflection distance inside the field region is negligible and ensures that the assumption of collimation of the proton trajectories in deriving Equation (1) is valid. In other situations when the maximum of
$\unicode[STIX]{x1D6FF}n/n_{0}\approx 0$
. This indicates that the deflection distance inside the field region is negligible and ensures that the assumption of collimation of the proton trajectories in deriving Equation (1) is valid. In other situations when the maximum of
![]() $\unicode[STIX]{x1D6FF}n/n_{0}$
approaches 1 or even higher, or the deflection distance inside the field region is too large to be ignored, the differences between the two deflection velocities in Figure 4(c) could be more evident[Reference Du and Wang24].
$\unicode[STIX]{x1D6FF}n/n_{0}$
approaches 1 or even higher, or the deflection distance inside the field region is too large to be ignored, the differences between the two deflection velocities in Figure 4(c) could be more evident[Reference Du and Wang24].
![]() $\hat{u} _{ye}(k_{x})$
is obtained by taking the Fourier transform of the deflection velocity
$\hat{u} _{ye}(k_{x})$
is obtained by taking the Fourier transform of the deflection velocity
![]() $u_{ye}(x)$
in Figure 4(c). The extracted one-dimensional energy spectrum of the magnetic field
$u_{ye}(x)$
in Figure 4(c). The extracted one-dimensional energy spectrum of the magnetic field
![]() $E_{Be}(k_{x})$
is then obtained by substituting
$E_{Be}(k_{x})$
is then obtained by substituting
![]() $\hat{u} _{ye}(k_{x})$
into Equation (22), i.e.,
$\hat{u} _{ye}(k_{x})$
into Equation (22), i.e.,
![]() $E_{B}(k_{x})=(4\unicode[STIX]{x1D70B}/l_{z}l_{x})(\unicode[STIX]{x1D6FE}m_{p}/q)^{2}k_{x}\hat{\boldsymbol{u}}_{y}^{2}(k_{x})$
, shown as the blue line in Figure 3.
$E_{B}(k_{x})=(4\unicode[STIX]{x1D70B}/l_{z}l_{x})(\unicode[STIX]{x1D6FE}m_{p}/q)^{2}k_{x}\hat{\boldsymbol{u}}_{y}^{2}(k_{x})$
, shown as the blue line in Figure 3.
We can see from Figure 3 that the amplitude and the envelope shape of the extracted magnetic field energy spectrum are approximately equal to the pre-set ones. Ten peaks are found in the energy spectrum of the pre-set magnetic field, marked with red numbers in Figure 3, respectively. For every red peak, a corresponding peak with a very close wavelength can be found in the extracted energy spectrum, marked with blue numbers. For most regions of the magnetic energy spectrum, the red and blue lines have either close amplitudes (specifically refer to the regions around peaks 5, 6, 7, 9, 10) or close peak–valley-averaged amplitudes (specifically refer to regions around peaks 1, 2, 3, 4, 8). This validates the use of Equation (22).
In the extracted spectrum, peaks 1 and 2 have close wavelengths and evidently higher amplitudes when compared to the other peaks in the blue line. Therefore, the extracted main wavelength for the magnetic energy is taken from the average wavelength of peaks 1 and 2. The result shows that
![]() $\unicode[STIX]{x1D706}_{|B|^{2}e}\approx 74~\unicode[STIX]{x03BC}\text{m}$
. According to Equation (24), the main wavelength for the magnetic field then equals
$\unicode[STIX]{x1D706}_{|B|^{2}e}\approx 74~\unicode[STIX]{x03BC}\text{m}$
. According to Equation (24), the main wavelength for the magnetic field then equals
![]() $\unicode[STIX]{x1D706}_{|B|e}\approx 74~\unicode[STIX]{x03BC}\text{m}$
. This extracted value is quite close to the pre-set one, i.e.,
$\unicode[STIX]{x1D706}_{|B|e}\approx 74~\unicode[STIX]{x03BC}\text{m}$
. This extracted value is quite close to the pre-set one, i.e.,
![]() $\unicode[STIX]{x1D706}_{|B|p}\approx 86~\unicode[STIX]{x03BC}\text{m}$
. The extracted mean strength of the magnetic field is calculated by Equation (23) with the blue energy spectrum in Figure 3. It gives
$\unicode[STIX]{x1D706}_{|B|p}\approx 86~\unicode[STIX]{x03BC}\text{m}$
. The extracted mean strength of the magnetic field is calculated by Equation (23) with the blue energy spectrum in Figure 3. It gives
![]() $B_{r\text{mse}}\approx 5.08~\text{T}$
, which agrees well with the pre-set value, i.e.,
$B_{r\text{mse}}\approx 5.08~\text{T}$
, which agrees well with the pre-set value, i.e.,
![]() $B_{\text{rmsp}}\approx 4.51~\text{T}$
.
$B_{\text{rmsp}}\approx 4.51~\text{T}$
.
It is necessary to mention that our theoretical analyses predict that the energy spectra are strictly equal for an ideal stochastic magnetic field; the difference between the two energy spectra in Figure 3 could be the result of a lack of stochasticity of the magnetic field. For an ideal stochastic distribution, the spectrum obtained from the Fourier transforms could be very smooth. However, the spectrum obtained from our pre-set magnetic field in Figure 2(a) shows ten small peaks over the large envelope, which indicates that the magnetic field distribution is not an ideal one. Actually, the stochastic fields in our simulations are generated with two hundred randomly distributed magnetic field tubes of the same magnitude and structure. It is hard to build an ideal stochastic field with those tubes. That is the reason which leads to the small differences between
![]() $B_{r\text{mse}}\approx 5.08~\text{T}$
and
$B_{r\text{mse}}\approx 5.08~\text{T}$
and
![]() $B_{\text{rmsp}}\approx 4.51~\text{T}$
, and between
$B_{\text{rmsp}}\approx 4.51~\text{T}$
, and between
![]() $\unicode[STIX]{x1D706}_{|B|e}\approx 74~\unicode[STIX]{x03BC}\text{m}$
and
$\unicode[STIX]{x1D706}_{|B|e}\approx 74~\unicode[STIX]{x03BC}\text{m}$
and
![]() $\unicode[STIX]{x1D706}_{|B|p}\approx 86~\unicode[STIX]{x03BC}\text{m}$
. Nevertheless, the matching of the positions of the ten peaks and the clearly seen envelope on the spectra all indicates that the magnetic field is still a stochastic one, though not an ideal one.
$\unicode[STIX]{x1D706}_{|B|p}\approx 86~\unicode[STIX]{x03BC}\text{m}$
. Nevertheless, the matching of the positions of the ten peaks and the clearly seen envelope on the spectra all indicates that the magnetic field is still a stochastic one, though not an ideal one.
Comprehensively examining the consistency between the pre-set values and the extracted results, we conclude that the method demonstrated above is applicable for extracting the main wavelength and mean strength of the Weibel-instability-generated magnetic field with proton radiography.
6 Discussion
In the above demonstration, some ideal model simplifications are assumed. The situations in experiment, however, could be much more complicated.
In this paper, all the probe protons have the same kinetic energy and are emitted from the source at the same time. Experimentally, the proton probes used in the radiography are mostly generated through the target normal sheath acceleration mechanism. The difference in the proton emission time and energy spread can broaden the probe duration. Generally, the probe pulse duration can reach about one picosecond[Reference Macchi, Borghesi and Passoni27]. Also, the amplitudes and spatial structures of the magnetic field may not be static, and could change during the growth of the Weibel instability[Reference Stockem, Grismayer, Fonseca and Silva13]. The extracted strength and wavelength are actually time-averaged results of the real ones. When the magnetic field evolves slowly during the passage of the proton probe, the strength and wavelength extraction method demonstrated above could yield time resolution using radiochromatic film stacks as the proton detector. However, if the magnetic field evolves rapidly during the passage of the proton probe, the extraction method will fail. This should be noticed especially in the growth stage of the Weibel instability and when the Weibel instability growth rate is large. Nevertheless, this strength and wavelength extraction method for the Weibel-instability-generated magnetic field is mostly capable after saturation of the instability. For an ion-driven Weibel instability, the magnetic field duration can be as long as several nanoseconds after it has been stimulated, and the probe pulse duration of several picoseconds has a negligible impact on the time resolution of the radiography[Reference Tzoufras, Ren, Tsung, Tonge, Mori, Fiore, Fonseca and Silva14]. For Weibel instability driven by electron thermal anisotropy, mostly investigated with an expanding plasma in the interaction of a laser pulse with a solid target, the magnetic field duration after saturation can also reach the range of several tens of picoseconds, which is also large enough to neglect the influence introduced by the probe pulse duration[Reference Thaury, Mora, Héron, Adam and Antonsen15].
At the same time, as has been discussed in Section 4, this extraction method is based on the assumption of two-dimensional isotropy and stochasticity of the magnetic field. However, in some circumstances, this assumption cannot be ensured and the magnetic field strength and wavelength extraction method demonstrated above may fail. For example, at the end of the nonlinear stage of the Weibel instability, merging of the current filaments is serious. There could be only several current filaments remaining, in which case two-dimensional isotropy and stochasticity are no longer fulfilled. Nevertheless, under such cases, the Faraday rotation method is capable of inferring the magnetic field strength and has been successfully applied in experiments[Reference Zhou, Bai, Tian, Sun, Cao and Liu28].
7 Conclusion
A method to infer the strength and wavelength of the Weibel-instability-generated magnetic field from the proton radiography has been demonstrated in our paper. With theoretical analyses, it is found that in the proton radiography of a Weibel-instability-induced magnetic field, which is usually two-dimensionally isotropic and stochastic, the proton flux density perturbation on the detection plane can be related to the energy spectrum of the magnetic field. It further allows us to obtain the mean strength and main wavelength of the magnetic field. Using ray tracing methods, a proton beam has been emitted numerically to simulate radiography of a two-dimensionally isotropic and stochastic magnetic field with the pre-set main wavelength equal to approximately
![]() $86~\unicode[STIX]{x03BC}\text{m}$
and the pre-set mean strength equal to approximately 4.51 T. With our extraction method, the main wavelength and mean strength of the magnetic field, when inferred from the detected proton density perturbation, are about
$86~\unicode[STIX]{x03BC}\text{m}$
and the pre-set mean strength equal to approximately 4.51 T. With our extraction method, the main wavelength and mean strength of the magnetic field, when inferred from the detected proton density perturbation, are about
![]() $74~\unicode[STIX]{x03BC}\text{m}$
and 5.08 T, respectively. The consistency between the pre-set values and the extracted results suggests that, through the extraction method demonstrated in our paper, the mean strength and main wavelength of the two-dimensionally isotropic and stochastic magnetic field can be inferred well from proton radiography. This could be helpful in first experimental measurements of the strength and wavelength of the Weibel-instability-generated stochastic magnetic field.
$74~\unicode[STIX]{x03BC}\text{m}$
and 5.08 T, respectively. The consistency between the pre-set values and the extracted results suggests that, through the extraction method demonstrated in our paper, the mean strength and main wavelength of the two-dimensionally isotropic and stochastic magnetic field can be inferred well from proton radiography. This could be helpful in first experimental measurements of the strength and wavelength of the Weibel-instability-generated stochastic magnetic field.
Acknowledgements
This work was supported by the Science Challenge Project (No. TZ2016005), the National Natural Science Foundation of China (Nos. 11575030 and U1730449 (NSAF)) and the National Key Programme for S&T Research and Development in China (No. 2016YFA0401100).