1. Introduction
Flares and coronal mass ejections (CMEs) are two energetic solar phenomena with static magnetic field energy in the solar atmosphere impulsively released as electromagnetic radiations and plasma thermal and kinetic energies through magnetic reconnection (MR), of which process flares and CMEs are generally accepted as different but strongly coupled manifestations[Reference Zhang1–Reference Shibata and Ugai5]. Investigations in virtue of multi-wavelength observations[Reference Pick6,Reference Savage7] have revealed moving CMEs and flare arcades, and a bright current sheet extending between them[Reference Savage7–Reference Tsuneta10]. It appears that the current sheet (hereafter referred to as the secondary CS) is induced by the behavior of the plasmoids moving away and stretching the surrounding magnetic fields, as described by the standard CSHKP model[Reference Carmichael and Hess11–Reference Kopp and Pneuman14]. As to the origin of CMEs, Shibata is the first person who, by statistically examining the correlation among characteristics of 15 Masuda-type solar flares, arrived at the conclusion that CMEs are initially the plasmoids gestated from a mother current sheet (or the primary CS). This statement has a theoretical basis. Numerical simulations with a magnetohydrodynamic (MHD) model and fully kinetic model indicate that the laminar layer is actually unstable when the Lundquist number ![]() $S= {\mu }_{0} L{V}_{A} / \eta \gt 1{0}^{4} $ or
$S= {\mu }_{0} L{V}_{A} / \eta \gt 1{0}^{4} $ or ![]() ${\gt }1{0}^{3} $ for the MHD model and the kinetic model, respectively, causing multi-level islands or plasmoids within the current sheet[Reference Samtaney15,Reference Daughton16] , and a much faster reconnection than the classical Sweet–Parker model[Reference Sweet and Lehnert17,Reference Parker18] . Here,
${\gt }1{0}^{3} $ for the MHD model and the kinetic model, respectively, causing multi-level islands or plasmoids within the current sheet[Reference Samtaney15,Reference Daughton16] , and a much faster reconnection than the classical Sweet–Parker model[Reference Sweet and Lehnert17,Reference Parker18] . Here, ![]() $L$ is the typical scale of the plasma,
$L$ is the typical scale of the plasma, ![]() ${V}_{A} $ the Alfvén velocity,
${V}_{A} $ the Alfvén velocity, ![]() $\eta $ the resistivity, and
$\eta $ the resistivity, and ![]() ${\mu }_{0} $ the permeability of free space. With a finite possibility, a single anomalous plasmoid with diameter around
${\mu }_{0} $ the permeability of free space. With a finite possibility, a single anomalous plasmoid with diameter around ![]() $0. 1L$ is predicted[Reference Uzdensky19], possibly providing the interpretation of the coronal mass ejections.
$0. 1L$ is predicted[Reference Uzdensky19], possibly providing the interpretation of the coronal mass ejections.
The precise relationship between MR, solar flares and CMEs still remains a topic of ongoing debate because of the lack of suitable observation data from space[Reference Bemporad20–Reference Lin23]. On the other hand, theoretical and numerical methods still have difficulties in explaining CMEs quantitatively rather than morphologically and qualitatively[Reference Moore21,Reference Lynch24] . Even predictions of the formation of plasmoid in the MR current layer by various kinds of numerical simulations still require further observational and direct experimental evidence in the laboratory[Reference Samtaney15,Reference Uzdensky19,Reference Raftery22,Reference Lin23] . In such situations, independent experimental inspections in a laboratory are required for testing and refining our understanding of the physical mechanisms underlying astronomic observations[Reference Remington, Arnett, Drake and Takabe25]. In this article, we present our recent observations of the plasmoid ejection from the MR current sheet produced by two mutually approaching laser-produced plasma bubbles[Reference Zhong26–Reference Nilson28]. The plasmoid is expected to mimic the CMEs, and its behavior of stretching the primarily reconnected magnetic field lines to produce a secondary MR current sheet and two bright ridges (enlightened magnetic loops) is found for the first time in a laboratory, which is expected to mimic solar flares.
2. Experiments
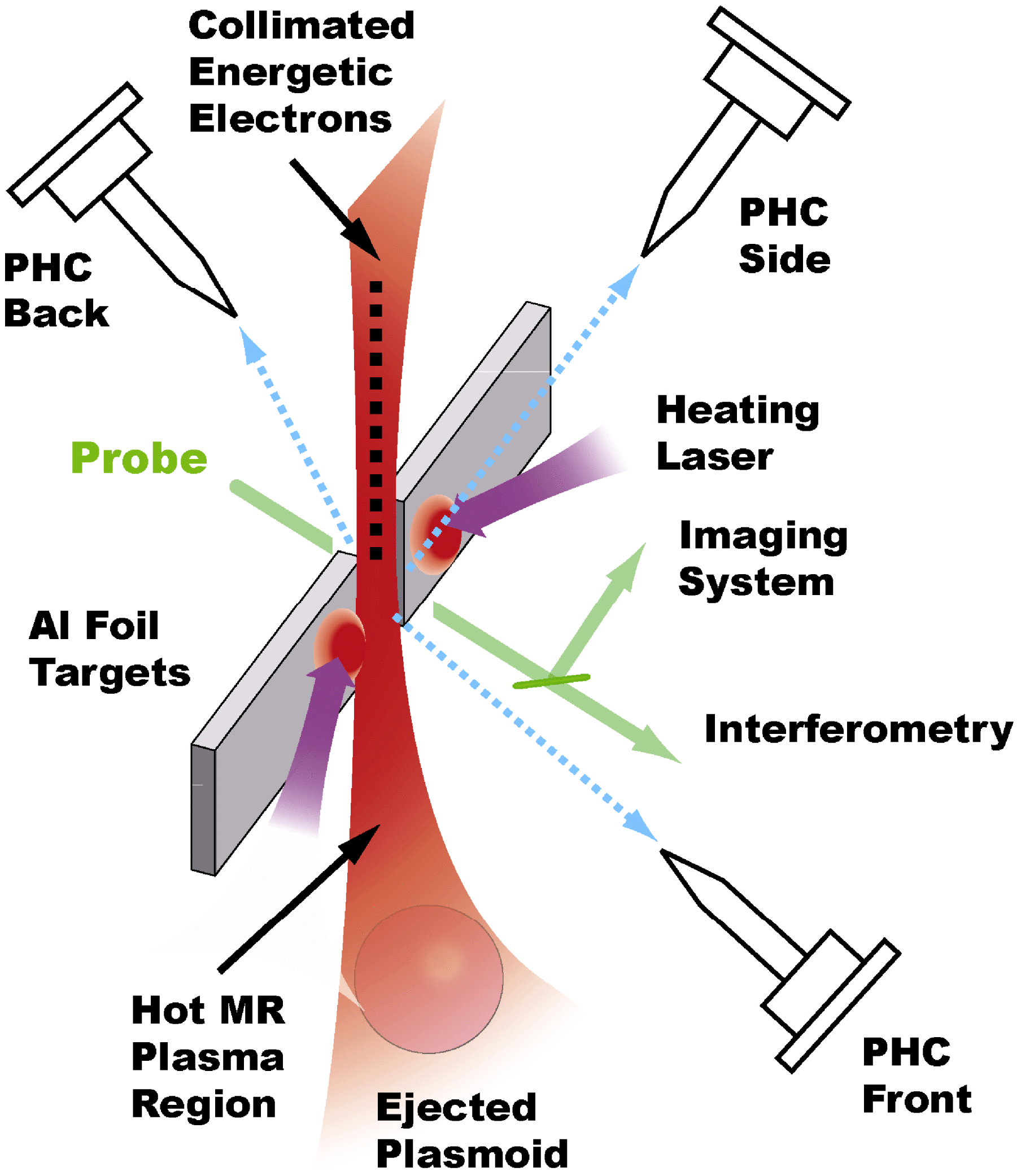
The experiment was performed on the SG-II laser facility. The setup of the experiments is illustrated schematically in Figure 1. Four heater beams at wavelength of 527 nm, shaped temporally with 0.9 ns flat top and 0.1 ns ramp front and tail, respectively, were divided into two groups of equal energy around 450 J, and focused by ![]() $F= 3$ optics simultaneously (within
$F= 3$ optics simultaneously (within ![]() ${\pm }25~\mathrm{ps} $) on two
${\pm }25~\mathrm{ps} $) on two ![]() $50~\mathrm{\mu} \mathrm{m} $-thick Al foil targets. The two Al foil targets had sizes of
$50~\mathrm{\mu} \mathrm{m} $-thick Al foil targets. The two Al foil targets had sizes of ![]() $0. 7~\mathrm{mm} \times 0. 3~\mathrm{mm} $ in the horizontal and vertical direction, respectively, and were separated from each other in the horizontal direction by a gap between
$0. 7~\mathrm{mm} \times 0. 3~\mathrm{mm} $ in the horizontal and vertical direction, respectively, and were separated from each other in the horizontal direction by a gap between ![]() $150$ and
$150$ and ![]() $240~\mathrm{\mu} \mathrm{m} $. The two focal spots were measured to have diameters less than
$240~\mathrm{\mu} \mathrm{m} $. The two focal spots were measured to have diameters less than ![]() $150~\mathrm{\mu} \mathrm{m} $ FWHM, giving an average laser intensity of order
$150~\mathrm{\mu} \mathrm{m} $ FWHM, giving an average laser intensity of order ![]() $1{0}^{14} {\unicode{x2013}} 1{0}^{15} ~\mathrm{W} . {\mathrm{cm} }^{- 2} $. While the distance between two laser spots was variable, we focused on the situation with the laser–spot separation of
$1{0}^{14} {\unicode{x2013}} 1{0}^{15} ~\mathrm{W} . {\mathrm{cm} }^{- 2} $. While the distance between two laser spots was variable, we focused on the situation with the laser–spot separation of ![]() $400\pm 25~\mathrm{\mu} \mathrm{ms} $. The main diagnostic for the laser-plasma density profile was a modified Nomarski interferometer with magnification of 3.5 and a spatial resolution of
$400\pm 25~\mathrm{\mu} \mathrm{ms} $. The main diagnostic for the laser-plasma density profile was a modified Nomarski interferometer with magnification of 3.5 and a spatial resolution of ![]() $25~\mathrm{\mu} \mathrm{ms} $. An imaging system was used to monitor the plasma profile. The 9th branch of SG-II facility, centered at 532 nm in a Gaussian profile of 150 ps, was used as the probe propagating perpendicularly to the target surface at various delays with respect to the four heater beams. A combination of reflective and bandpass (
$25~\mathrm{\mu} \mathrm{ms} $. An imaging system was used to monitor the plasma profile. The 9th branch of SG-II facility, centered at 532 nm in a Gaussian profile of 150 ps, was used as the probe propagating perpendicularly to the target surface at various delays with respect to the four heater beams. A combination of reflective and bandpass (![]() $\Delta \lambda \sim 2~\mathrm{nm} $) interference filters was used to reduce the detectable self-emission from the target. Three pinhole cameras with magnification of 10 were used for monitoring the X-ray emission from the front, back and side of target plasmas, respectively.
$\Delta \lambda \sim 2~\mathrm{nm} $) interference filters was used to reduce the detectable self-emission from the target. Three pinhole cameras with magnification of 10 were used for monitoring the X-ray emission from the front, back and side of target plasmas, respectively.
3. Morphology comparisons
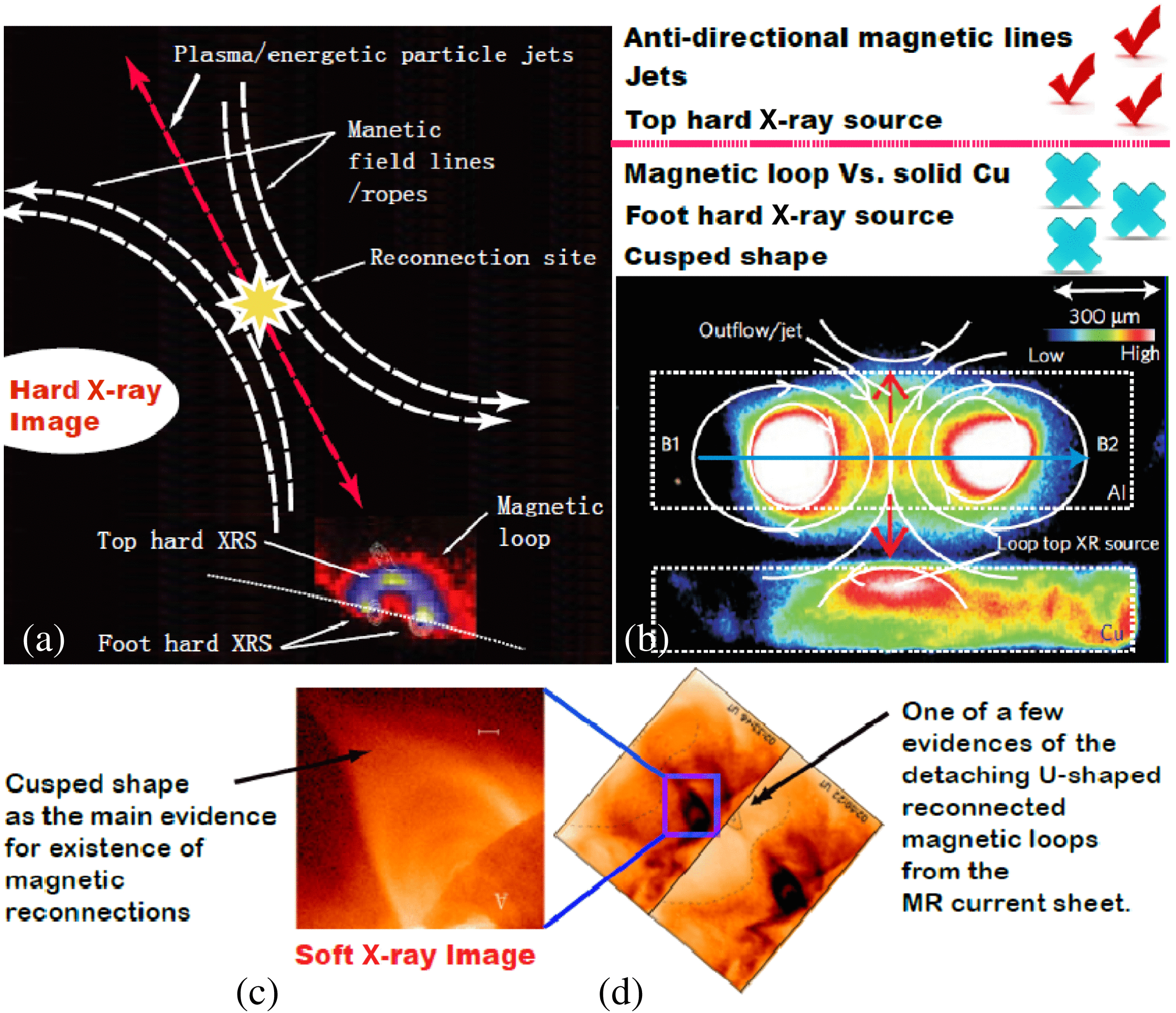
We would like to recall our previous work of modeling loop-top X-ray source and reconnection outflows in solar flares on the SG-II laser facility in 2009[Reference Zhong26]. The motivation for this subject was from hard-X-ray observations of the bright spot on the top of the magnetic loop, and the laser–plasma experiments performed for MR jet investigations by Nilson et al. and Li et al.[Reference Li27,Reference Nilson28] . The experimental goal and design are so simple that, by setting a solid Cu target in the direction of the expected MR outflow, one would expect that on the obstacle surface there would be a bright spot with an area comparable to the width of the ion diffusion region if the outflow really is ejected there with enough kinetic energy. Figure 2 shows the comparison between the solar observations and the present experimental results. Figure 2(a) shows the hard-X-ray image of the top X-ray source as well as the two foot X-ray sources on the magnetic loop (see the lower right corner). The sketch in Figure 2(a) invokes the magnetic reconnection to explain the formation of the loop-top X-ray source[Reference Masuda29,Reference Innes30] . Figure 2(b) gives the experimental results, showing the bright spot on the Cu obstacle surface suggesting the existence of energetic flow possibly due to the magnetic reconnection based on the related theoretical calculation with the measured plasma properties.

Figure 1. Schematic illustration of the experiment setup. Three pinhole cameras were installed to monitor laser–plasmas from the back, front and side, respectively. Modified Nomarski interferometry applying a 532 nm laser beam in 150 ps Gaussian pulse was used as the main diagnostic in the front of the target to measured the plasma density. An imaging system with magnification ratio of 1.5 was used to monitor the target plasma profile.

Figure 2. Detailed comparisons between the solar phenomena and the experimental results. (a) shows the loop-top hard-X-ray spot as well as the two loop-foot spots, with the sketch indicating the invoked magnetic reconnection as the cause; (b) is the experimental results with a bright X-ray spot on the Cu target initially set in the path of the expected MR outflow; (c) shows the Yohkoh-recorded cusp-shaped magnetic loop at the end of the MR current sheet near the solar photospheric surface, and (d) the detaching U-shaped magnetic loop from the other end of the current sheet.

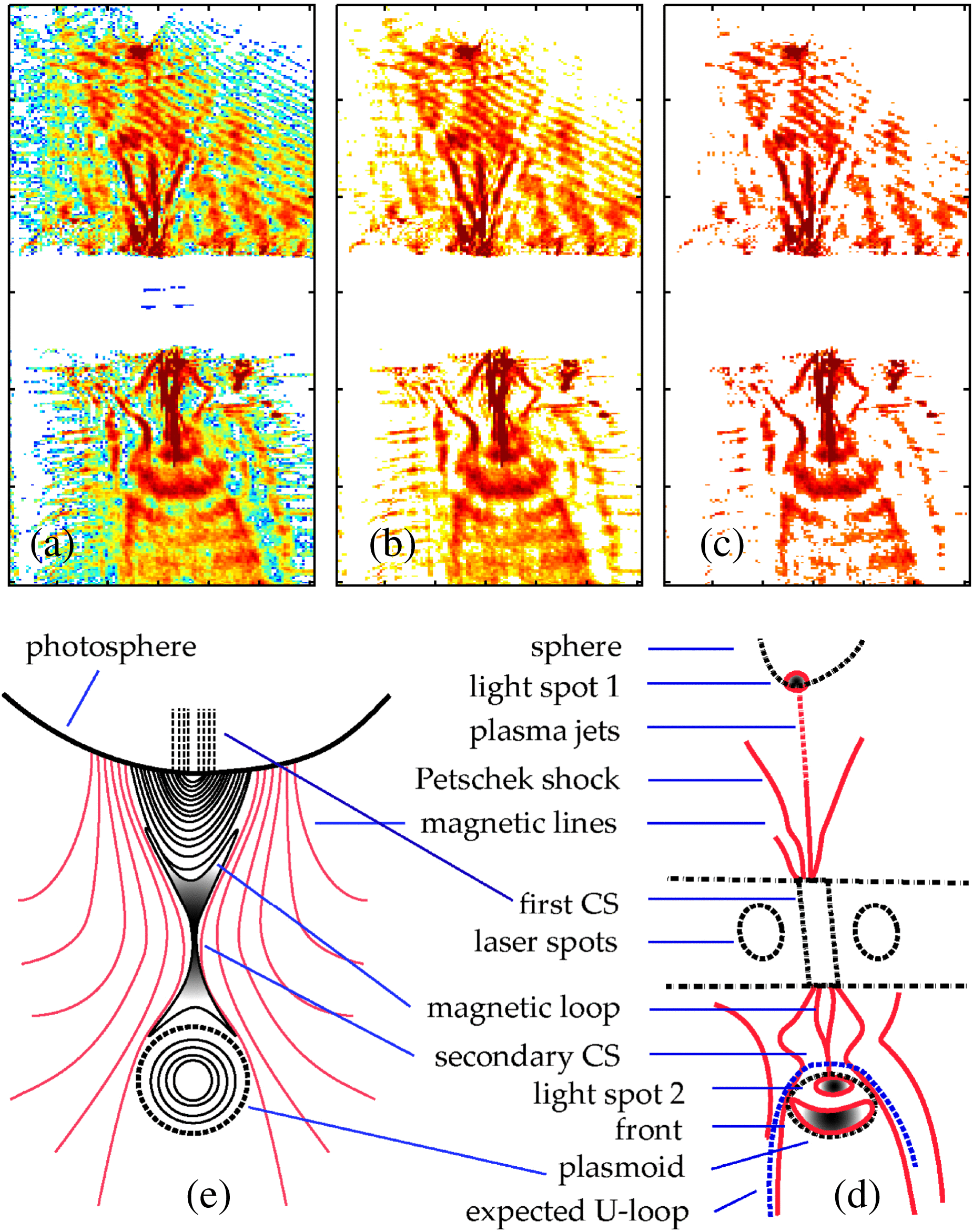
Figure 3. Plasma images taken at 532 nm. (a) is the raw image. (b) is produced by the pre-measured background correction to (a), while (c) is produced from (a) in the same way, but with 25% extra intensity enhancement in the background. (d) is the schematic image structure with enlightened magnetic separatrices and bright areas in (c) represented by solid lines. (e) Schematic diagram of a disrupted magnetic field forming in the breakout CME scenario. (d) and (e) are compared component by component as the notes indicate.
The previous work is the first experiment that shows the possibility of studying solar-phenomenon-related physics in a laboratory by using Ryutov’s scaling methods. However, from the viewpoint of experiments, we would like to compare the experimental results with solar observations in detail. While the experimental results do indicate that the MR process can eject an outflow energetic enough to ionize the solid target, there are some items which should be clarified between the experimental results and solar phenomena. First, the solar hard-X-ray source is located on the top of a magnetic-confined plasma, or the loop, while the laboratory bright spot represents a plasma produced by the collision between the energetic outflow and a solid target. This intrinsic difference between the solar and the laboratory physical processes leads to the distinguishable characteristic of the solar flare with the two foot hard-X-ray bright spots produced by the MR-ejected energetic electrons propagating along the reconnecting magnetic field lines, which could never happen if only the solid target is used to simulate the magnetized plasma. Second, in the experiments there is no hard evidence for the existence of the magnetic reconnection process, like the situation of solar observations where a cusp-shaped bright loop is recognized as the MR evidence. Figure 2(c) and (d) show the related soft-X-ray images of the solar flares, which present the cusp-shaped magnetic loop at the end of the MR current sheet near the photospheric surface (Figure 2(c)), and the detaching U-shaped loop from the other end (Figure 2(d)).
So, can we carry out laboratory experiments to produce the phenomena with detailed structures that reproduce the solar or astrophysical observations, but without any eisegesis? Our research work with the SG-II laser facility in 2010 carried on the experimental design philosophy, trying to consummate the laboratory investigation of the physics behind the solar flares.
Figure 3(a) gives the raw plasma image taken at 532 nm. Figure 3(b) is produced from Figure 3(a) through the pre-measured background correction. Figure 3(c) is produced in the same way but with 25% extra intensity enhancement in the background. Figure 3(c) is produced by subtracting a background with 25% extra intensity enhancements. For clear signatures to be emphasized, a schematic picture of the experimental image is given in Figure 3(d), with solid lines representing the bright lines, or bright area edges if closed lines used. It is clear that the graph has two kinds of features above and below the line connecting the two laser focal spots, respectively. The upper half part of the image presents an MR picture as Petschek’s model predicts: the separatrices between the private and the public regions consist of slow-mode shocks (SMSs), with the short diffusion region ending at the crossing point of the SMSs (see Figure 3(d))[Reference Petschek and Thorne31]. The X-ray image of the diffusion region recorded with one X-ray pinhole camera also presents the SMS fronts and the X-ray emission enhancement at the middle of the two laser foci (not shown here). The angle between the two slow-mode shock fronts is estimated as ![]() $2{\theta }_{rec} \sim 35\hspace{0.167em} \pm \hspace{0.167em} {5}^{\circ } $. Between the two bright SMS fronts, a third bright line is present, indicating a well-collimated energetic electron beam produced from the diffusion regions (or the primary CS). The Petschek shocks were confirmed by different kinds of numerical simulation and astronomic observation. Tsuneta et al. observed shocks in X-ray images of the flare on 23 February 1992[Reference Tsuneta32]. The recently measured higher density structure surrounding the MR current sheet also revealed the formation of two facing Petschek slow-mode shocks[Reference Phan33,Reference Bemporad34] . Besides the Petschek SMSs, we would also like to identify the three bright lines as three electron diffusion regions (EDRs)[Reference Dong35]. The central well-collimated EDR can then find its counterpart observations in the magnetosheath region downstream of the Earth bow shock[Reference Phan36], and the two EDRs on the edges had theirs reported by Mozer et al. [Reference Mozer37].
$2{\theta }_{rec} \sim 35\hspace{0.167em} \pm \hspace{0.167em} {5}^{\circ } $. Between the two bright SMS fronts, a third bright line is present, indicating a well-collimated energetic electron beam produced from the diffusion regions (or the primary CS). The Petschek shocks were confirmed by different kinds of numerical simulation and astronomic observation. Tsuneta et al. observed shocks in X-ray images of the flare on 23 February 1992[Reference Tsuneta32]. The recently measured higher density structure surrounding the MR current sheet also revealed the formation of two facing Petschek slow-mode shocks[Reference Phan33,Reference Bemporad34] . Besides the Petschek SMSs, we would also like to identify the three bright lines as three electron diffusion regions (EDRs)[Reference Dong35]. The central well-collimated EDR can then find its counterpart observations in the magnetosheath region downstream of the Earth bow shock[Reference Phan36], and the two EDRs on the edges had theirs reported by Mozer et al. [Reference Mozer37].
The lower half part of the image presents much more complicated features. As a whole, the fan-like region is confined by the two slow-mode shocks (or EDRs) as in the upper part, partially determined by the symmetrical configuration of the whole system. The detailed structure includes a bright current sheet (the secondary CS), beneath which exists a plasmoid with a bright spot on the top of it, a dark cavity, and then a bright edge located at its front. The bright spot on the top of the plasmoid is also connected to the bright current sheet. Attached to the other end of the bright current sheet are two bright ridges with foot points located on the ending points of the diffusion region of the primary CS between the two mutually approaching plasma bubbles.
The lower part of the experimental image is comparable to solar observations, in which specific post-CME features detected in X-ray images and white-light coronagraphs have been identified as the current sheet connecting the flare loops and the CME core[Reference Temmer2,Reference Lin8,Reference Ko9,Reference Raftery22,Reference Nishida38] . A schematic picture of CME observations is given in Figure 3(e) for comparison. In the present experiments, the plasmoid is gestated within the primary CS, which is consistent with Shibata’s model and numerical simulations[Reference Shibata39,Reference Shimizu40] . The plasmoid is observed well after the primary MR observed with the SMSs as the signature. The experimental observation confirms the theoretical prediction of possible generation of anomalous plasmoids from a current sheet by Uzdensky et al. [Reference Uzdensky19]. It also indicates that the primary MR is capable of providing the central magnetic arcade needed in the breakout model by Antiochos[Reference Lynch24,Reference Antiochos41] , naturally rather than through assumptions artificially. After being ejected out of the primary current sheet, the moving-away plasmoid stretches the primary reconnected magnetic field, inducing the secondary MR current sheet accelerating the local plasma. This stage mimics the second acceleration stage of the CMEs in the astronomic observations by Raftery et al. [Reference Raftery22] and Lin et al. [Reference Lin23], in which energetic electron jets with higher speed than the plasmoid/CMEs, when catching and colliding with the high-density plasmoid, produce a bright spot as is apparent in the present experiments. Energetic electrons with MeV energy, which propagate spirally along the secondary reconnected magnetic separatrices/SMS fronts, emit synchrotron radiation as observed in the flare-like profile (see below for more).
The plasmoid eruption from the primary CS and its behavior of stretching the primarily reconnected magnetic field are attested by the vis-á-vis curved bright lines for which the primary separatrices/SMS fronts act as the asymptotic curves when comparing characteristics of the upper and the lower parts of the image (Figure 3(c) and (d)). The bright lines are believed to be a fraction of the reconnected magnetic field lines previously existing in the SMS fronts similar to that in the upper part of the graph. The elbows of the two curved bright lines are right near the bright current sheet, while the foot points of them are located at the endpoint of the diffusion region of the primary MR. In solar CMEs, people have also observed a stringy, concave-outward U-loop half-circling the ejected plasmoid from the bottom and suspected that the U-loop in these cases might represent a detached magnetic field formed by reconnected open field lines or very high loops, or some kinds of wave front with unclear generation mechanism[Reference Wang and Sheeley42]. Rather than a complete U-loop as observed in some solar flares, however, what is observed in the present experiments is a plasmoid that is not yet completely detached from the secondary current sheet within the observation duration. The characteristics of the present experimental results confirm the generation mechanism of the astronomically observed U-loop or V-loop profile[Reference Wang and Sheeley42,Reference Simnett43] near the outside end of the current sheet as the reconnected magnetic field lines detached from the surroundings.
4. Euler similarity and dissipation differences
We also compare quantitatively the laser–plasma system to the solar flare plasmas by checking the Euler similarity between the two systems, to make sure that their important aspects evolve dynamically in a similar fashion[Reference Remington, Drake and Ryutov44]. The laser–plasma owns a Euler number ![]() $E{u}_{LP} = L/ \tau \sqrt{\rho / P} \sim 8. 4$ by taking its characteristic length
$E{u}_{LP} = L/ \tau \sqrt{\rho / P} \sim 8. 4$ by taking its characteristic length ![]() $L= 0. 1~\mathrm{cm} $, typical time scale
$L= 0. 1~\mathrm{cm} $, typical time scale ![]() $\tau \sim 1~\mathrm{ns} $, the measured electron density
$\tau \sim 1~\mathrm{ns} $, the measured electron density ![]() ${n}_{e} \sim 1{0}^{19} {\unicode{x2013}} 1{0}^{20} ~{\mathrm{cm} }^{- 3} $, and electron temperature
${n}_{e} \sim 1{0}^{19} {\unicode{x2013}} 1{0}^{20} ~{\mathrm{cm} }^{- 3} $, and electron temperature ![]() ${T}_{e} \sim 400~\mathrm{eV} $. Here,
${T}_{e} \sim 400~\mathrm{eV} $. Here, ![]() $\rho $ is plasma mass density, and
$\rho $ is plasma mass density, and ![]() $P= {n}_{e} {k}_{B} {T}_{e} $ is the plasma pressure. The other parameter is the plasma
$P= {n}_{e} {k}_{B} {T}_{e} $ is the plasma pressure. The other parameter is the plasma ![]() $\beta = 8\pi P/ {B}^{2} \sim 0. 1$ by taking the spontaneous magnetic field
$\beta = 8\pi P/ {B}^{2} \sim 0. 1$ by taking the spontaneous magnetic field ![]() $B\sim 1~\mathrm{MG} $. Both the above parameters can find corresponding values for solar flare plasmas with conditions in the range provided by[Reference Bray45], indicating the hydrodynamic similarity between the two systems. As to the effects of viscosity and heat conduction in the laser–plasma system, the Reynolds number and the Péclet number are calculated to be
$B\sim 1~\mathrm{MG} $. Both the above parameters can find corresponding values for solar flare plasmas with conditions in the range provided by[Reference Bray45], indicating the hydrodynamic similarity between the two systems. As to the effects of viscosity and heat conduction in the laser–plasma system, the Reynolds number and the Péclet number are calculated to be ![]() $R{e}_{LP} \sim 500$ and
$R{e}_{LP} \sim 500$ and ![]() $P{e}_{LP} \sim 10{\unicode{x2013}} 100$, respectively, ensuring the laser–plasma system as a hydrodynamic fluid. For the solar flare plasmas, however,
$P{e}_{LP} \sim 10{\unicode{x2013}} 100$, respectively, ensuring the laser–plasma system as a hydrodynamic fluid. For the solar flare plasmas, however, ![]() $R{e}_{SP} \sim 1{0}^{8} $ and
$R{e}_{SP} \sim 1{0}^{8} $ and ![]() $P{e}_{SP} \sim 1{0}^{7} $. The significant differences in effects of viscosity and heat conduction indicate that, although the two hydrodynamic systems evolve identically in a scaled sense, there might be differences in the dissipative mechanisms, as will be shown later in the electron acceleration process.
$P{e}_{SP} \sim 1{0}^{7} $. The significant differences in effects of viscosity and heat conduction indicate that, although the two hydrodynamic systems evolve identically in a scaled sense, there might be differences in the dissipative mechanisms, as will be shown later in the electron acceleration process.
In solar flares, recent studies report energetic electrons with energy around 10 MeV[Reference Mewaldt46,Reference Klassen47] , while half of the released energy is carried by electrons with energy between 20 and 100 keV[Reference Lin48]. Theoretical study suggests that Fermi acceleration related to volume-filling contracting magnetic islands is the dominant mechanism for the electron acceleration process, which is confirmed by observed links between energetic electrons and magnetic islands explored by four Cluster spacecraft crossing the Earth’s magnetotail[Reference Drake49,Reference Chen50] . Recent observed reconnection in a magnetic cloud boundary layer, however, determined that energetic electrons are accelerated by the reconnected electric fields, combining with a Fermi-type mechanism[Reference Wang51]. The measured energy spectra of electrons take the form of a power law in both observations. For the present experiments, direct measurements of energetic electrons accelerated from the MR diffusion region also indicate that the energy of electron can reach several MeV in a power-law scaling. For relativistic electrons gyrating in the magnetic fields, i.e., the SMS fronts in the present experiments, the synchrotron radiation wavelength is related to the electron energy by ![]() ${E}_{max} = {m}_{e} {c}^{2} \mathop{(2. 5\times 1{0}^{- 2} / {\lambda }_{max} B)}\nolimits ^{1/ 2} $, and the gyroradius of the relativistic electrons is
${E}_{max} = {m}_{e} {c}^{2} \mathop{(2. 5\times 1{0}^{- 2} / {\lambda }_{max} B)}\nolimits ^{1/ 2} $, and the gyroradius of the relativistic electrons is ![]() ${r}_{g} = 1. 70\times 1{0}^{3} \sqrt{\mathop{({E}_{max} / 0. 511)}\nolimits ^{2} - 1. 0} / B$, where
${r}_{g} = 1. 70\times 1{0}^{3} \sqrt{\mathop{({E}_{max} / 0. 511)}\nolimits ^{2} - 1. 0} / B$, where ![]() ${m}_{e} $ is the electron mass,
${m}_{e} $ is the electron mass, ![]() $c$ the speed of light in vacuum, and
$c$ the speed of light in vacuum, and ![]() ${\lambda }_{max} = 532~\mathrm{nm} $ the wavelength at which the synchrotron radiation presents the maximum intensity. It is reasonable to take the thickness of the SMS fronts as the electron gyroradius,
${\lambda }_{max} = 532~\mathrm{nm} $ the wavelength at which the synchrotron radiation presents the maximum intensity. It is reasonable to take the thickness of the SMS fronts as the electron gyroradius, ![]() ${r}_{g} \sim 55~\mathrm{\mu} \mathrm{m} $; then the energy of the relativistic electrons is determined as 5.2 MeV, and the reconnected spontaneous magnetic field as 375 T.
${r}_{g} \sim 55~\mathrm{\mu} \mathrm{m} $; then the energy of the relativistic electrons is determined as 5.2 MeV, and the reconnected spontaneous magnetic field as 375 T.
According to the Fermi acceleration model, or the diffusive shock acceleration (DSA) model, the acceleration time of particles to energy ![]() ${E}_{max} $ is
${E}_{max} $ is ![]() ${\tau }_{acc} \sim 6. 7\eta c{E}_{max} / ZeB{ V}_{sk}^{2} $, with
${\tau }_{acc} \sim 6. 7\eta c{E}_{max} / ZeB{ V}_{sk}^{2} $, with ![]() $Ze$ as the particle charge,
$Ze$ as the particle charge, ![]() ${V}_{sk} $ as the shock speed, and
${V}_{sk} $ as the shock speed, and ![]() $\eta $ as the parameter characterizing the efficiency of diffusion. For coronal plasmas, electrons need seconds or minutes to be accelerated to energy in the range 0.1–10 MeV if taking
$\eta $ as the parameter characterizing the efficiency of diffusion. For coronal plasmas, electrons need seconds or minutes to be accelerated to energy in the range 0.1–10 MeV if taking ![]() $\eta \sim 1{\unicode{x2013}} 1{0}^{4} $, which is consistent with the observed flare time, indicating the dominance of Fermi acceleration in impulsive solar energetic electrons, as discussed above[Reference Mewaldt46,Reference Klassen47,Reference Drake49,Reference Chen50] . For the present laser–plasma system, however, electrons with MeV energy can only be achieved after tens of nanoseconds or microseconds if the DSA mechanism dominates the acceleration process even with the assumption of Bohm diffusion as
$\eta \sim 1{\unicode{x2013}} 1{0}^{4} $, which is consistent with the observed flare time, indicating the dominance of Fermi acceleration in impulsive solar energetic electrons, as discussed above[Reference Mewaldt46,Reference Klassen47,Reference Drake49,Reference Chen50] . For the present laser–plasma system, however, electrons with MeV energy can only be achieved after tens of nanoseconds or microseconds if the DSA mechanism dominates the acceleration process even with the assumption of Bohm diffusion as ![]() $\eta \sim 1$. Such acceleration time is much longer than the experimentally observed flare time
$\eta \sim 1$. Such acceleration time is much longer than the experimentally observed flare time ![]() ${\sim }100$ ps of the current sheet and the two bright ridges. So rather than the Fermi-type mechanism, a much more efficient method is expected to explain the generation of energetic electrons in such a time scale. Numerical simulations have suggested that, with a single X-line configuration such as in the present system, the electron can be accelerated to ultrahigh energy by the reconnected electric field[Reference Drake52–Reference Wang55]. For electrons to obtain energy as high as several MeV in
${\sim }100$ ps of the current sheet and the two bright ridges. So rather than the Fermi-type mechanism, a much more efficient method is expected to explain the generation of energetic electrons in such a time scale. Numerical simulations have suggested that, with a single X-line configuration such as in the present system, the electron can be accelerated to ultrahigh energy by the reconnected electric field[Reference Drake52–Reference Wang55]. For electrons to obtain energy as high as several MeV in ![]() ${\sim }100~\mathrm{ps} $, the electric field needs to be
${\sim }100~\mathrm{ps} $, the electric field needs to be ![]() ${\sim }1{0}^{8} ~\mathrm{V} / \mathrm{m} $, and the effective displacement to be
${\sim }1{0}^{8} ~\mathrm{V} / \mathrm{m} $, and the effective displacement to be ![]() ${\sim }~\mathrm{cm} $. Such an electric field in the present system corresponds to the magnetic annihilation of tens of tesla within 0.1 ns according to Faraday’s law
${\sim }~\mathrm{cm} $. Such an electric field in the present system corresponds to the magnetic annihilation of tens of tesla within 0.1 ns according to Faraday’s law ![]() $\bigtriangledown \times \mathbf{E} = - \partial \mathbf{B} / \partial t$, indicating a reconnection rate between 0.1 and 0.3, which is consistent with the rate calculated by the measured magnetic exhaust wedge angle tan
$\bigtriangledown \times \mathbf{E} = - \partial \mathbf{B} / \partial t$, indicating a reconnection rate between 0.1 and 0.3, which is consistent with the rate calculated by the measured magnetic exhaust wedge angle tan![]() ${\theta }_{rec} \sim 0. 25{\unicode{x2013}} 0. 35$. A large displacement is also possible but only if electrons exhibit behaviors of gyration in the magnetic field, or re-enter the electric field circularly due to reflection by the quasi-static magnetic fields. This is the actual situation in the present experiments, where the electric field of the MR diffusion region occupies only a small part of the whole magnetic topology, both of which in conjunction construct practically a cyclotron, which accelerates electrons efficiently, as observed in experiments. Different from solar flare plasmas, here in the laser-plasma systems, electrons gain energy predominantly from the electric field, while the multiple bouncing behavior between moving fronts and ends of plasmoids help to trap electrons in the accelerating location. To understand To understand details of the electron acceleration during MR, further investigations with time-resolved electron energy spectra measurements will be necessary.
${\theta }_{rec} \sim 0. 25{\unicode{x2013}} 0. 35$. A large displacement is also possible but only if electrons exhibit behaviors of gyration in the magnetic field, or re-enter the electric field circularly due to reflection by the quasi-static magnetic fields. This is the actual situation in the present experiments, where the electric field of the MR diffusion region occupies only a small part of the whole magnetic topology, both of which in conjunction construct practically a cyclotron, which accelerates electrons efficiently, as observed in experiments. Different from solar flare plasmas, here in the laser-plasma systems, electrons gain energy predominantly from the electric field, while the multiple bouncing behavior between moving fronts and ends of plasmoids help to trap electrons in the accelerating location. To understand To understand details of the electron acceleration during MR, further investigations with time-resolved electron energy spectra measurements will be necessary.
5. Summary
In summary, impulsive solar flares and CMEs can be simulated in a laboratory by using two mutually approaching laser–plasma bubbles, as validated by the remarkable similarity between the two systems in morphology. In the present experiments, the theoretically predicted anomalous plasmoid from the primary MR current sheet is demonstrated, which is expected to act as the possible initiation of CMEs if scaling the laboratory plasmas to astronomic plasmas. The behavior of the plasmoid/CMEs moving away and stretching the primarily reconnected magnetic fields into a secondary MR current sheet and flares of two bright ridges is also observed, providing the possible explanation or attestation to the relationship between the formation of solar flares and plasmoid/CMEs. The U-loop profile around the plasmoid/CMEs, which is observed in some solar cases but not very often, is confirmed as the detached reconnected magnetic lines in the present experiments as well as in the solar observations. However, the large difference of characteristic dimensionless parameters in the two systems leads to different relative values of typical scales for dissipative mechanisms. While energetic electrons from solar flares are generally accepted to be accelerated by stochastic processes related to Fermi mechanisms, electrons in the present experiments, with energy as high as their counterpoints, is predominantly accelerated efficiently by the reconnected electric field combined with the magnetic fields surrounding the small diffusion region, or within the moving plasmoids.
Acknowledgements
This work is jointly supported by the National Natural Science Foundation of China (Nos. 11121504, 11074297, 11274152), the CAS project of KJCX2-YWT01, and the National Basic Research Program of China (No. 2007CB815101). The authors also thank all staff of the National Laboratory on High Power Lasers and Physics.