1 Introduction
High-power laser facilities have been established for research on inertial confinement fusion (ICF), high-energy-density (HED) physics, laboratory-scale astrophysics, etc. [Reference Betti and Hurricane1–Reference Casner, Rigon, Albertazzi, Michel, Pikuz, Faenov, Mabey, Ozaki, Sakawa, Sano, Ballet, Tzeferacos, Lamb, Falize, Gregori and Koenig4]. Typical examples of such facilities include the National Ignition Facility (NIF) in the USA[Reference Moses, Lindl, Spaeth, Patterson, Sawicki, Atherton, Baisden, Lagin, Larson, MacGowan, Miller, Rardin, Roberts, Van Wonterghem and Wegner5–Reference Miller, Moses and Wuest7], the ShenGuang-II (SG-II) Facility in China[Reference Zhu, Xie, Sun, Kang, Yang, Guo, Zhu, Zhu, Gao, Liang, Cui, Yang, Zhang and Lin8, Reference Gao, Ma, Zhu, Cao, Zhu, Yang, Dai and Lin9], and the Laser Megajoule Facility (LMJ) in France[Reference Miquel, Lion and Vivini10, Reference Vivini and Nicolaizeau11]. The basic principle of most of the studies performed at high-power laser facilities is to simultaneously focus many amplified high-energy laser pulses onto a small target to achieve extremely high pressure and temperature, comparable to that inside a star, to investigate nuclear fusion and other high-energy-physics processes. To achieve a high energy injection ratio, an amplified pulse laser beam at 1053 nm should be converted to the third harmonic (351 nm) in the final optical assembly (FOA)[Reference Jiao, Shao, Zhao, Wu, Ji, Wang, Xia, Liu, Zhou, Ju, Cai, Ye, Qiao, Hua, Li, Pan, Ren, Sun, Zhu and Lin12, Reference Wegner, Auerbach, Biesiada, Dixit, Lawson, Menapace, Parham, Swift, Whitman and Williams13] before being focused onto a target. A frequency converter based on sum-frequency generation is composed of one doubler and one tripler, and thus the excitation laser beam always includes the fundamental frequency (1053 nm), and the second (526.5 nm) and third (351 nm) harmonic frequencies. The energy and quality of the converted third-harmonic laser beam of the high-power laser facility are the two most important parameters for all laser-physics experiments, and accordingly measurements on them are routine work in the operation and maintenance of the laser facility. Though the fundamental and second-harmonic laser beams do not directly take part in physical experiments, by measuring the complex amplitude of the fundamental, second- and third-harmonic beams simultaneously, we can accurately analyze the energy distribution, the frequency conversion efficiency, the characteristics of nonlinear crystals, and other important parameters of laser facility. However, because of the very limited inner space of the laser drivers and the characteristics of the laser beams, it has been previously impossible to simultaneously measure all these three laser beams using conventional techniques, and only the third harmonic has been typically measured in practice. An intensity imaging method was commonly used to measure the near-field and far-field intensity distributions of high-power laser beams[Reference Zacharias, Beer, Bliss, Burkhart, Cohen, Sutton, Van Atta, Winters, Salmon, Stolz, Pigg and Arnold14]. However, because of the limited dynamic range of the detector, only the central lobe of focal spot can be measured in most cases. In theory, measurement of the phase of laser beams can be carried out with an interferometer or Shack–Hartmann sensor; however, because of their disadvantages in complex optical configurations, stringent requirements on working environment, and limited number of sub-apertures, it has been very difficult to use interferometers or Shack–Hartmann sensors to measure the phase of high-power laser beams, which consist of a single laser pulse propagating inside a tube with a time duration of several nanoseconds[Reference Zacharias, Beer, Bliss, Burkhart, Cohen, Sutton, Van Atta, Winters, Salmon, Stolz, Pigg and Arnold14, Reference Bromage, Bahk, Irwin, Kwiatkowski, Pruyne, Millecchia, Moore and Zuegel15]. Coherent diffraction imaging (CDI) was developed mainly for imaging with X-rays and other short wavelengths to address the problem of the lack of high-quality optics in this spectral regime[Reference Fienup16–Reference Miao, Charalambous, Kirz and Sayre18]. CDI can directly reconstruct the amplitude and phase of the radiation field from a diffraction intensity pattern via an iterative algorithm without the need for high-quality optics including lenses. It has outstanding advantages, including a compact optical structure and simple operation. Several investigations have been performed to demonstrate that CDI is a very promising technique for online laser beam diagnosis in high-power laser facilities[Reference Bahk, Bromage, Begishev, Mileham, Stoeckl, Storm and Zuegel19, Reference Matsuoka and Yamakawa20]. As a recently developed CDI technique, coherent modulation imaging (CMI)[Reference Zhang and Rodenburg21, Reference Zhang, Chen, Morrison, Vila-Comamala, Guizar-Sicairos and Robinson22] facilitates accurate measurement of the intensity and phase distributions of a roughly convergent radiation beam by simply positioning a random phase plate in the vicinity of the focal region, followed by the acquisition of a single frame of diffraction patterns. The advantages of CMI, which include an extremely compact structure and single exposure measurement, make it an ideal tool for online high-power laser beam diagnosis. In this regard, the results of several studies have demonstrated its practical merits[Reference Pan, Veetil, Liu, Tao, Jiang, Lin, Li and Zhu23, Reference Tao, Veetil, Pan, Liu and Zhu24]. Although the original CMI technique can only measure the complex amplitude of a single wavelength, we have previously demonstrated that a light field of two wavelengths can also be accurately measured using this approach by utilizing a multi-mode algorithm to perform the reconstruction[Reference Dong, Pan, Liu and Zhu25]. In this report, it is shown that by replacing the binary-value phase plate with a multi-value plate, a hybrid laser beam consisting of the wavelengths 1053 nm, 526.5 nm and 351 nm can be measured via the same approach. This is an ideal technique to analyze high-power laser beams behind the FOAs of the laser drivers. The validity of this proposed online diagnosis method was verified using both numerical simulations and experimental measurements. Proof-of-principle experiments were performed using a mini laser driver platform consisting of one pulsed-laser operating at 1053 nm, one doubler, and one tripler. It was shown that the spatial resolution and measurement accuracy can approach
![]() $125~\unicode[STIX]{x03BC}\text{m}$
and 0.2 wavelengths, respectively, for 1053 nm.
$125~\unicode[STIX]{x03BC}\text{m}$
and 0.2 wavelengths, respectively, for 1053 nm.
2 Methods
2.1 Phase modulator design
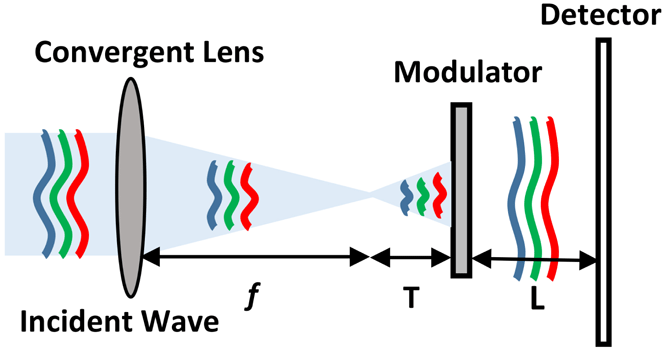
Figure 1(a) is a schematic representation of the principle of CMI, where the incident light beam illuminates a phase modulator, and the exiting field from the modulator forms diffraction patterns on a detector. As the key component of CMI, the phase modulator determines the convergence speed of the iterative computation and the final reconstruction accuracy. To obtain fully developed speckle patterns on the detector plane, the phase modulator of the CMI should be a highly scattering element for each wavelength. For single-wavelength CMI, the phase modulator is usually fabricated by constructing many tiny squares on a silica glass plate using an optical etching technique. The tiny light-transmitting squares have a phase redundancy of
![]() $\unicode[STIX]{x1D70B}$
. When all these squares are randomly distributed on the glass surface, the phase modulator will act as a binary-valued strongly scattering pure phase object. To measure the hybrid light field behind the FOAs, the phase modulator should be strongly scattering for each wavelength, and thus the structure of the modulator should be specially designed.
$\unicode[STIX]{x1D70B}$
. When all these squares are randomly distributed on the glass surface, the phase modulator will act as a binary-valued strongly scattering pure phase object. To measure the hybrid light field behind the FOAs, the phase modulator should be strongly scattering for each wavelength, and thus the structure of the modulator should be specially designed.

Figure 1. (a) Diagram of the CMI layout. The incident wave illuminates the phase modulator, which diffracts the observed light field into a speckle pattern. The speckle pattern and an iterative algorithm are used to retrieve the complex amplitude of the incident wave. (b) The designed three-step random phase plate. (c) One-dimensional diagram of (b).
Figure 1(b) shows a three-step random phase plate, where the tiny square has two different heights,
![]() $h_{1}$
and
$h_{1}$
and
![]() $h_{2}$
. Then for light with a wavelength of
$h_{2}$
. Then for light with a wavelength of
![]() $\unicode[STIX]{x1D706}$
, two different phase redundancies of
$\unicode[STIX]{x1D706}$
, two different phase redundancies of
![]() $\unicode[STIX]{x1D711}_{1}=2\unicode[STIX]{x1D70B}[h_{1}(n-1)/\unicode[STIX]{x1D706}]$
and
$\unicode[STIX]{x1D711}_{1}=2\unicode[STIX]{x1D70B}[h_{1}(n-1)/\unicode[STIX]{x1D706}]$
and
![]() $\unicode[STIX]{x1D711}_{2}=2\unicode[STIX]{x1D70B}[h_{2}(n-1)/\unicode[STIX]{x1D706}]$
will be generated. The substrate material of the random phase plate used in this study is fused silica with a refractive index of 1.4498 at 1053 nm; thus,
$\unicode[STIX]{x1D711}_{2}=2\unicode[STIX]{x1D70B}[h_{2}(n-1)/\unicode[STIX]{x1D706}]$
will be generated. The substrate material of the random phase plate used in this study is fused silica with a refractive index of 1.4498 at 1053 nm; thus,
![]() $h_{1}$
and
$h_{1}$
and
![]() $h_{2}$
are 1171 nm and 585.5 nm, respectively. Therefore,
$h_{2}$
are 1171 nm and 585.5 nm, respectively. Therefore,
![]() $\unicode[STIX]{x1D711}_{1}$
will take the values of
$\unicode[STIX]{x1D711}_{1}$
will take the values of
![]() $\unicode[STIX]{x1D70B}$
,
$\unicode[STIX]{x1D70B}$
,
![]() $2\unicode[STIX]{x1D70B}$
and
$2\unicode[STIX]{x1D70B}$
and
![]() $3\unicode[STIX]{x1D70B}$
for wavelengths of 1053 nm, 526.5 nm and 351 nm, respectively, while
$3\unicode[STIX]{x1D70B}$
for wavelengths of 1053 nm, 526.5 nm and 351 nm, respectively, while
![]() $\unicode[STIX]{x1D711}_{2}$
will take the values
$\unicode[STIX]{x1D711}_{2}$
will take the values
![]() $\unicode[STIX]{x1D70B}/2$
,
$\unicode[STIX]{x1D70B}/2$
,
![]() $\unicode[STIX]{x1D70B}$
and
$\unicode[STIX]{x1D70B}$
and
![]() $3\unicode[STIX]{x1D70B}/2$
for wavelengths of 1053 nm, 526.5 nm and 351 nm, respectively. Therefore, for 526.5 nm the phase modulator is still a binary-valued phase object with a phase redundancy of 0 and
$3\unicode[STIX]{x1D70B}/2$
for wavelengths of 1053 nm, 526.5 nm and 351 nm, respectively. Therefore, for 526.5 nm the phase modulator is still a binary-valued phase object with a phase redundancy of 0 and
![]() $\unicode[STIX]{x1D70B}$
. The phase modulator generates phase redundancies of
$\unicode[STIX]{x1D70B}$
. The phase modulator generates phase redundancies of
![]() $[0,\unicode[STIX]{x1D70B}/2,\unicode[STIX]{x1D70B}]$
for 1053 nm and
$[0,\unicode[STIX]{x1D70B}/2,\unicode[STIX]{x1D70B}]$
for 1053 nm and
![]() $[0,3\unicode[STIX]{x1D70B}/2,3\unicode[STIX]{x1D70B}]$
for 351 nm.
$[0,3\unicode[STIX]{x1D70B}/2,3\unicode[STIX]{x1D70B}]$
for 351 nm.
2.2 Algorithm
Figure 2 shows the flowchart of three-wavelength CMI, where
![]() $E_{k,n}(r_{s})$
,
$E_{k,n}(r_{s})$
,
![]() $E_{k,n}(r_{M})$
and
$E_{k,n}(r_{M})$
and
![]() $E_{k,n}(r_{D})$
are the complex amplitudes of the
$E_{k,n}(r_{D})$
are the complex amplitudes of the
![]() $k$
th wavelength in the
$k$
th wavelength in the
![]() $n$
th iteration on the support plane, the modulator plane and the detector plane, respectively. Iterative reconstruction starts after three random initial guesses are proposed for the three different light fields incident on the modulator plane, and the iteration continues with the following steps until the reconstruction error is smaller than a predetermined value.
$n$
th iteration on the support plane, the modulator plane and the detector plane, respectively. Iterative reconstruction starts after three random initial guesses are proposed for the three different light fields incident on the modulator plane, and the iteration continues with the following steps until the reconstruction error is smaller than a predetermined value.

Figure 2. Flowchart of the reconstruction process.
(1) The
![]() $k$
th
$k$
th
![]() $(k=1,2,3)$
incident wave on the modulator is multiplied by the transmission function of the modulator
$(k=1,2,3)$
incident wave on the modulator is multiplied by the transmission function of the modulator
![]() $T_{k}$
,
$T_{k}$
,
![]() $E_{k,n}(r_{M})=E_{k,n}(r_{m})\cdot T_{k}$
, where
$E_{k,n}(r_{M})=E_{k,n}(r_{m})\cdot T_{k}$
, where
![]() $r_{m}$
and
$r_{m}$
and
![]() $r_{M}$
represent the plane before and after the modulator, respectively. Then
$r_{M}$
represent the plane before and after the modulator, respectively. Then
![]() $E_{k,n}(r_{M})$
is propagated to the detector plane
$E_{k,n}(r_{M})$
is propagated to the detector plane
![]() $E_{k,n}(r_{D})=\Im \{E_{k,n}(r_{M})|L_{2}\}$
, where the operator
$E_{k,n}(r_{D})=\Im \{E_{k,n}(r_{M})|L_{2}\}$
, where the operator
![]() $\Im \{E_{k,n}(r_{M})|L_{2}\}$
denotes numerical wave propagation over a distance
$\Im \{E_{k,n}(r_{M})|L_{2}\}$
denotes numerical wave propagation over a distance
![]() $L_{2}$
.
$L_{2}$
.
(2) The difference between the recorded diffraction pattern
![]() $I$
and the reconstructed wave at the diffraction plane is calculated using Equation (1). The reconstruction process will stop if the error is smaller than a predetermined target value.
$I$
and the reconstructed wave at the diffraction plane is calculated using Equation (1). The reconstruction process will stop if the error is smaller than a predetermined target value.
where
![]() $\sum _{u}$
represents summation over the entire diffraction plane.
$\sum _{u}$
represents summation over the entire diffraction plane.
(3) Application of modulus constraints with the recording pattern
![]() $I$
at the detector plane.
$I$
at the detector plane.
Compared to single-wavelength CMI, we adopt a different Fourier constraint where the modulus of each wavelength is scaled by its real energy while its own phase is preserved. The denominator of Equation (2) represents the intensity summation of all wavelengths.
(4) Saturation processing is applied using Equation (3) for each wavelength, where
![]() $S$
denotes the saturated region in the diffraction pattern
$S$
denotes the saturated region in the diffraction pattern
![]() $I$
, and the iterative calculation value is preserved before applying the Fourier constraint in this area. In the unsaturated region, the updated value after application of the Fourier constraint is used.
$I$
, and the iterative calculation value is preserved before applying the Fourier constraint in this area. In the unsaturated region, the updated value after application of the Fourier constraint is used.
(5) Backpropagation of the light field of each wavelength to the modulator plane
![]() $\hat{E}_{k,n}(r_{M})=\Im ^{-1}\{\hat{E}_{k,n}^{\prime }(r_{D})\mid L_{2}\}$
and the removal of the effect of the modulator.
$\hat{E}_{k,n}(r_{M})=\Im ^{-1}\{\hat{E}_{k,n}^{\prime }(r_{D})\mid L_{2}\}$
and the removal of the effect of the modulator.
where
![]() $\ast$
denotes the complex conjugate and
$\ast$
denotes the complex conjugate and
![]() $\unicode[STIX]{x1D6FC}$
is a parameter which can be adjusted to alter the step size of the update;
$\unicode[STIX]{x1D6FC}$
is a parameter which can be adjusted to alter the step size of the update;
![]() $\unicode[STIX]{x1D6FC}=1$
was used for all the presented results.
$\unicode[STIX]{x1D6FC}=1$
was used for all the presented results.
(6) Backpropagation to the support plane
![]() $\hat{E}_{k,n}(r_{S})=\Im ^{-1}\{\hat{E}_{k,n}(r_{m})\mid L_{1}\}$
and the application of the support constraint.
$\hat{E}_{k,n}(r_{S})=\Im ^{-1}\{\hat{E}_{k,n}(r_{m})\mid L_{1}\}$
and the application of the support constraint.
The support function
![]() $H_{D(k,n)}$
is a hole support and its diameter
$H_{D(k,n)}$
is a hole support and its diameter
![]() $D(k,n)$
increases with the iteration time until the designed maximum value is reached.
$D(k,n)$
increases with the iteration time until the designed maximum value is reached.
![]() $H_{D(k,n)}=1$
inside the hole and the value is zero outside the hole support.
$H_{D(k,n)}=1$
inside the hole and the value is zero outside the hole support.
![]() $\unicode[STIX]{x1D6FE}$
varies from 0 to 1 as an update weight value.
$\unicode[STIX]{x1D6FE}$
varies from 0 to 1 as an update weight value.
(7) Propagation of
![]() $\hat{E}_{k,n}^{\prime }(r_{S})$
to the modulator plane and repetition of the next iteration reconstruction until
$\hat{E}_{k,n}^{\prime }(r_{S})$
to the modulator plane and repetition of the next iteration reconstruction until
![]() $\text{Error}_{n}$
is reduced to a threshold value.
$\text{Error}_{n}$
is reduced to a threshold value.
3 Simulations and experiments
3.1 Simulation
The feasibility of our proposed method was initially examined using numerical simulations. Figure 3 is a schematic representation of the light path used for the simulation, where a collimated laser beam containing the three wavelengths 1053 nm, 526.5 nm and 351 nm is focused by an achromatic lens prior to illuminating the modulator. The diameter of the collimated laser beam is 6 mm, and the focal length
![]() $f$
of the lens is 150 mm. The distances from the modulator to the focal spot and the detector are 30 mm and 100 mm, respectively. The pixel size of the detector is assumed to be
$f$
of the lens is 150 mm. The distances from the modulator to the focal spot and the detector are 30 mm and 100 mm, respectively. The pixel size of the detector is assumed to be
![]() $9~\unicode[STIX]{x03BC}\text{m}\times 9~\unicode[STIX]{x03BC}\text{m}$
and the pixel number of the detector is assumed to be
$9~\unicode[STIX]{x03BC}\text{m}\times 9~\unicode[STIX]{x03BC}\text{m}$
and the pixel number of the detector is assumed to be
![]() $2048\times 2048$
.
$2048\times 2048$
.

Figure 3. Beam path diagram of the simulation. The incident wave consists of frequencies
![]() $1\unicode[STIX]{x1D714}$
,
$1\unicode[STIX]{x1D714}$
,
![]() $2\unicode[STIX]{x1D714}$
and
$2\unicode[STIX]{x1D714}$
and
![]() $3\unicode[STIX]{x1D714}$
simultaneously.
$3\unicode[STIX]{x1D714}$
simultaneously.

Figure 4. (a)–(c) Amplitudes and (d)–(f) phases of these three illumination beams incident on the modulator plane for (a), (d) 351 nm, (b), (e) 526.5 nm and (c), (f) 1053 nm.
Figure 4 shows the three incident beams on the modulator plane, where the panels (a)–(c) display the amplitude, and panels (d)–(f) display the corresponding phase. From left to right, the images correspond to 351 nm, 526.5 nm, and 1053 nm, respectively.

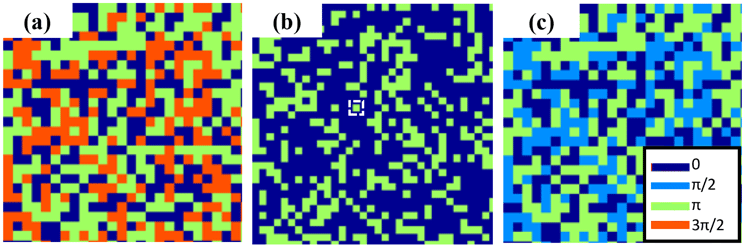
Figure 5. Phase delay of the modulator for (a) 351 nm, (b) 526.5 nm and (c) 1053 nm.
Figure 5 shows the transmitting phase structures of the modulator corresponding to the three different wavelengths 1053 nm, 526.5 nm and 351 nm. These three-phase structures are obtained by generating a random matrix with equally distributed values between zero and three, after rounding them to integers of 0, 1 and 2, then multiplying the matrix by
![]() $\unicode[STIX]{x1D70B}/4$
,
$\unicode[STIX]{x1D70B}/4$
,
![]() $\unicode[STIX]{x1D70B}/2$
and
$\unicode[STIX]{x1D70B}/2$
and
![]() $3\unicode[STIX]{x1D70B}/4$
, respectively. The size of the minimum square represented by a white square with dashed lines in Figure 5(b) is
$3\unicode[STIX]{x1D70B}/4$
, respectively. The size of the minimum square represented by a white square with dashed lines in Figure 5(b) is
![]() $9~\unicode[STIX]{x03BC}\text{m}\times 9~\unicode[STIX]{x03BC}\text{m}$
.
$9~\unicode[STIX]{x03BC}\text{m}\times 9~\unicode[STIX]{x03BC}\text{m}$
.
By multiplying the complex amplitudes shown in Figure 4 with their corresponding phase modulators and propagating them to the detector plane, the diffraction intensity can be calculated for each wavelength. Figures 6(a)–6(c) are the computed diffraction patterns for the wavelengths 351 nm, 526.5 nm and 1053 nm, respectively. Figure 6(d) is the summation of the three computed diffraction intensity patterns, which is the hybrid diffraction pattern recorded in practical experiments. The zoomed-in images of the central regions inside the dashed rectangles represent the speckle patterns as insets in the top-right corners.

Figure 6. Simulated diffraction patterns of (a) 351 nm, (b) 526.5 nm, (c) 1053 nm and (d) their summation, which is a hybrid diffraction pattern of the three wavelengths that provide simultaneous illumination. (e) Change in the corresponding reconstruction error for each wavelength throughout the iteration process.
Using the aforementioned reconstruction algorithm, the complex amplitudes of the three wavelengths can be iteratively determined, and their corresponding reconstructed accuracy can be calculated using Equation (6).
The change in the corresponding reconstruction error for each wavelength throughout the iteration process is represented in Figure 6(e). Based on this result, it is determined that the residual error becomes smaller than 1% for all three wavelengths within 120 iterations, and eventually decreases to 0.5% after 500 iterations. Visualization 1 available at https://doi.org/10.1017/hpl.2019.26 shows the dynamic changes of all these reconstructions. These simulation results clearly demonstrate the feasibility of the proposed method.

Figure 7. Three illuminations incident on the modulator plane for (a) 351 nm, (b) 526.5 nm, (c) 1053 nm with different lens aberrations.
To further demonstrate the feasibility and reliability of our method, we added another numerical simulation with different lens aberrations for each wavelength. Figure 7 shows these three illuminations on the modulator plane in the case of different lens aberrations, which are obviously different from each other. In addition, to demonstrate that this method can also provide additional information about three different fields, a phase plate etched with the two letters ‘SG’ was put into the incident beams, and thus the wavefronts of the plane waves were changed after passing through the phase plate as shown in Figure 8(A).

Figure 8. (A) Beam path diagram of the second simulation. The wavefronts behind the ‘SG’ phase plate for (a) 351 nm, (b) 526.5 nm and (c) 1053 nm. (d)–(f) plot their phase delay profile along the white line in (a)–(c), respectively. (g)–(i) display the amplitude of the three incident beams on the modulator plane.
Figures 8(a)–8(c) show the wavefronts after the ‘SG’ phase plate with wavelengths of 351 nm, 526.5 nm and 1053 nm, respectively. To intuitively illustrate the phase difference caused by the ‘SG’ phase plate, Figures 8(d)–8(f) plot their phase delay profile along the white line in Figures 8(a)–8(c), respectively. The values are 4.267, 2.751 and 1.342 in radians. It can be seen that there is a phase relationship which nearly equals double and third relationships according to the wavelength and the refractive index. Now we use this wave as the incident wave instead of plane waves and the lens has different aberrations for each wavelength, as mentioned above. The distance between the ‘SG’ phase plate and the convergent lens is 10 mm. The other parameters are consistent with the previous simulation. Figures 8(g)–8(i) show the amplitude of the three incident beams on the modulator plane.
Using our proposed method, the reconstructed results are shown in Figure 9. Panels (a)–(c) and (d)–(f) show the reconstructed modulus and phase distribution on the modulator plane, respectively; from left to right, they are for 351 nm, 526.5 nm and 1053 nm, respectively. By propagating these waves back to the convergent lens, removing the effect of this lens, and then back propagating to the ‘SG’ phase plate plane, we can obtain the wavefronts behind it, which are shown in Figures 9(g)–9(i). Figures 9(j)–9(l) plot the reconstructed phase delay profile along the white line in Figures 9(g)–9(i), showing the reconstructed phase delay values are 4.249, 2.745 and 1.337 in radians, which are consistent with the input values. These simulation results demonstrate the feasibility of the proposed method and simultaneously show that it can provide additional information, such as the phase relationship of the three different fields.

Figure 9. (a)–(c) Reconstructed modulus and (d)–(f) phase on the modulator plane for 351 nm, 526.5 nm and 1053 nm, respectively. (g)–(i) show the wavefronts behind the ‘SG’ phase plate. (j)–(l) plot the reconstructed phase delay profile along the white line in (g)–(i), respectively.
3.2 Experiments
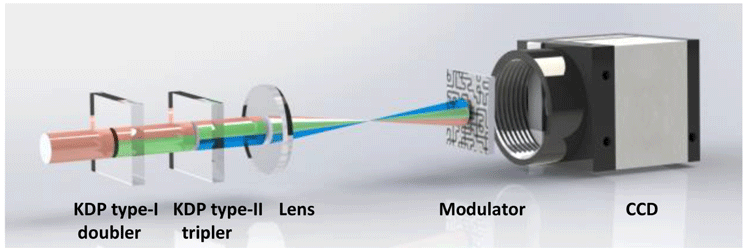
Our experimental setup shown in Figure 10 is a mini-scale FOA of the SG-II high-power laser arrangement. The laser beam of 1053 nm was incident on frequency conversion optics composed of a KDP type-I doubler and a KDP type-II tripler. After the KDP type-II tripler, the fundamental (1053 nm), second (526.5 nm) and third harmonic (351 nm) frequencies exist simultaneously. This hybrid laser beam from the tripler passes through an achromatic lens with a focal length of 250 mm, and is then incident on the modulator placed 56 mm behind the focus spot. A charge-coupled-device camera (Allied Vision Technology GE4000,
![]() $4008\times 2067$
pixels, pitch
$4008\times 2067$
pixels, pitch
![]() $9~\unicode[STIX]{x03BC}\text{m}$
) was placed downstream of the modulator to record the diffraction patterns at a distance of 88.1 mm behind the phase plate.
$9~\unicode[STIX]{x03BC}\text{m}$
) was placed downstream of the modulator to record the diffraction patterns at a distance of 88.1 mm behind the phase plate.

Figure 10. Experimental setup for measuring the fundamental, second and third harmonics in one snapshot.

Figure 11. (a)–(c) Reconstructed amplitude and (d)–(f) phase of the random phase plate for 351 nm, 526.5 nm and 1053 nm, respectively, using ptychography.
The transmission functions of the modulator for each wavelength were characterized by ePIE (extended ptychographic iterative engine)[Reference Maiden and Rodenburg26] in advance, and a positioning error correction algorithm[Reference Zhang, Peterson, Vila-Comamala, Berenguer, Bean, Chen, Menzel, Robinson and Rodenburg27, Reference Maiden, Humphry, Sarahan, Kraus and Rodenburg28] was used to improve the measurement accuracy. Figures 11(a)–11(c) display the reconstructed transmission amplitudes of the random phase plate for 351 nm, 526.5 nm and 1053 nm, respectively. Figures 11(d)–11(f) show the corresponding phase retardations.

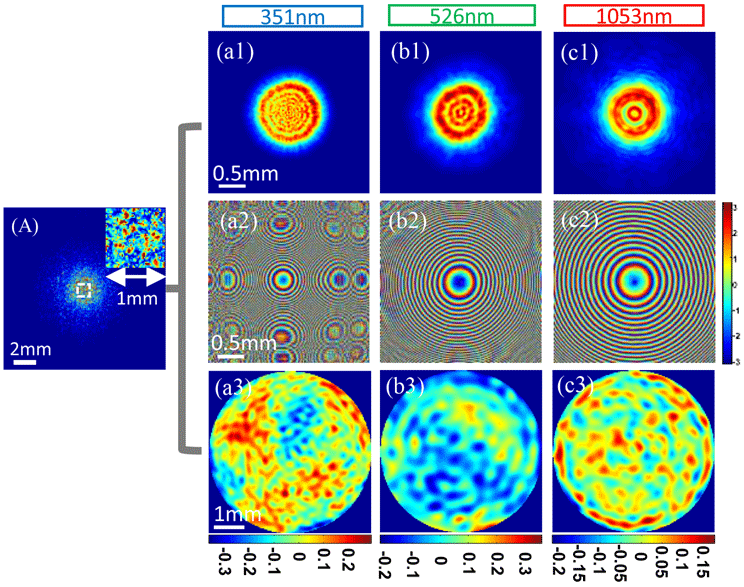
Figure 12. Recorded diffraction pattern (A) and reconstructed results of the three harmonics of the random phase plate with our proposed method. (a1)–(c1) Amplitude and (a2)–(c2) phase of 351 nm, 526.5 nm and 1053 nm, respectively. Wavefronts before the convergent lens for (a3) 351 nm, (b3) 526.5 nm and (c3) 1053 nm.
Figure 12(A) represents the recorded diffraction pattern, where the inset in the top-right corner is the zoomed-in region of the diffraction pattern identified with a white rectangle, in order to highlight the speckle pattern. Both the amplitude and phase of the three wavelengths of the hybrid laser beam can be simultaneously reconstructed using our proposed algorithm based on this recorded diffraction pattern. Figures 12(a1)–12(c1) represent the reconstructed modulus for 351 nm, 526.5 nm and 1053 nm, respectively, and Figures 12(a2)–12(c2) represent their corresponding phase. In the proof-of-principle experiment, laser beams at three wavelengths passing a hole were used to verify the feasibility of our method; the fine rings in the reconstructed intensity in Figures 12(a1)–12(c1) come from the edge diffraction of the hole. By propagating the reconstructed complex amplitude of three wavelengths from the random phase plate to the back plane of the lens in Figure 10, and subtracting the phase caused by the lens from them, we can get their wavefronts before the lens in Figures 12(a3)–12(c3), which correspond to wavelengths of 351 nm, 526.5 nm and 1053 nm, respectively. The peak-to-valley (PV) value of Figures 12(a3)–12(c3) are
![]() $0.1045\unicode[STIX]{x1D706}$
,
$0.1045\unicode[STIX]{x1D706}$
,
![]() $0.0916\unicode[STIX]{x1D706}$
and
$0.0916\unicode[STIX]{x1D706}$
and
![]() $0.0628\unicode[STIX]{x1D706}$
, respectively.
$0.0628\unicode[STIX]{x1D706}$
, respectively.
To examine the measurement accuracy of the aforementioned experiment, several experiments were performed to separately measure the complex amplitude of each wavelength using the conventional CMI method. By the introduction of an appropriate filter behind the tripler to allow only one wavelength to form diffraction patterns on the detector at a time, the diffraction patterns associated with the three wavelengths can be separately recorded. Subsequently, the conventional single-wavelength CMI algorithm can be utilized to reconstruct their complex amplitudes. The reconstructions are shown in Figure 13, where panels (a1)–(c1) represent the diffraction patterns recorded for the three wavelengths, and panels (a2)–(c2) and (a3)–(c3) correspond to the modulus and phase on the random phase plate for each wavelength, respectively. Compared to the results shown in Figure 12, they are highly consistent with each other.
Figures 13(a4)–13(c4) display the wavefronts before the convergent lens of 351 nm, 526.5 nm and 1053 nm and their PV values are
![]() $0.0759\unicode[STIX]{x1D706}$
,
$0.0759\unicode[STIX]{x1D706}$
,
![]() $0.0825\unicode[STIX]{x1D706}$
and
$0.0825\unicode[STIX]{x1D706}$
and
![]() $0.0411\unicode[STIX]{x1D706}$
, respectively.
$0.0411\unicode[STIX]{x1D706}$
, respectively.

Figure 13. Single-wavelength CMI results. (a1)–(c1) Recorded diffraction pattern associated with each wavelength. (a2)–(c2) Amplitude and (a3)–(c3) phase for 351 nm, 526.5 nm and 1053 nm, respectively. Wavefronts before the convergent lens for (a4) 351 nm, (b4) 526.5 nm and (c4) 1053 nm.
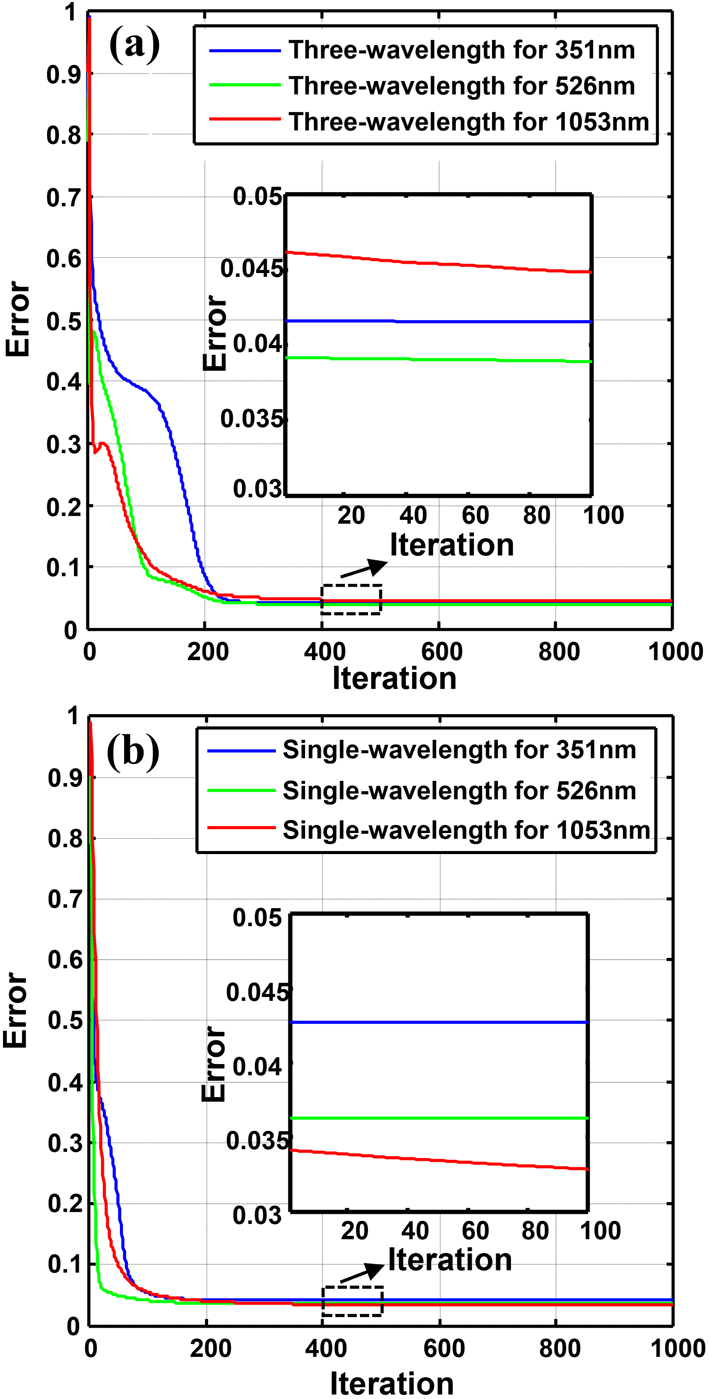
Additional calculations were performed to quantitatively analyze the reconstruction errors further. The reconstruction errors were computed using Equation (6), where the diffraction patterns
![]() $I_{k}$
of the
$I_{k}$
of the
![]() $k$
th wavelength can be recorded by blocking the other two wavelengths. Figure 14(a) represents the evaluation of the error curves as the iterations progress for the three wavelengths investigated and Figure 14(b) represents the change in reconstruction errors for common single-wavelength CMI. It is apparent that three-wavelength CMI has a slower convergence than single-wavelength CMI. Three-wavelength CMI can achieve reconstruction errors lower than 5% based on 300 iterations, while single-wavelength CMI can achieve the same reconstruction error using only 120 iterations. More unknown factors should be decided by three-wavelength CMI than by single-wavelength CMI. The zoomed-in error curves in Figure 14(b) show that three-wavelength CMI can achieve the same reconstruction error as single-wavelength CMI of approximately 4%, just beyond 400 iterations. This means that three-wavelength CMI has a comparable reconstruction accuracy to single-wavelength CMI, although more iterations were required in experiments. In above reconstructions, an NVIDIA Tesla K40c GPU was adopted to do the computation, taking nearly 0.62–0.65
$k$
th wavelength can be recorded by blocking the other two wavelengths. Figure 14(a) represents the evaluation of the error curves as the iterations progress for the three wavelengths investigated and Figure 14(b) represents the change in reconstruction errors for common single-wavelength CMI. It is apparent that three-wavelength CMI has a slower convergence than single-wavelength CMI. Three-wavelength CMI can achieve reconstruction errors lower than 5% based on 300 iterations, while single-wavelength CMI can achieve the same reconstruction error using only 120 iterations. More unknown factors should be decided by three-wavelength CMI than by single-wavelength CMI. The zoomed-in error curves in Figure 14(b) show that three-wavelength CMI can achieve the same reconstruction error as single-wavelength CMI of approximately 4%, just beyond 400 iterations. This means that three-wavelength CMI has a comparable reconstruction accuracy to single-wavelength CMI, although more iterations were required in experiments. In above reconstructions, an NVIDIA Tesla K40c GPU was adopted to do the computation, taking nearly 0.62–0.65
![]() $\text{s}$
to finish one round of iterative updating for three wavelengths. Figure 14(a) shows the convergence in reconstructing error versus iterations; we find that about 310 s (500 iterations) is required to get accurate reconstruction.
$\text{s}$
to finish one round of iterative updating for three wavelengths. Figure 14(a) shows the convergence in reconstructing error versus iterations; we find that about 310 s (500 iterations) is required to get accurate reconstruction.

Figure 14. Evolution of the error curve versus iterations. (a) Results of the three-wavelength CMI reconstruction error for 351 nm (blue), 526.5 nm (green) and 1053 nm (red). (b) Results for the single-wavelength CMI error using the same procedure as (a).
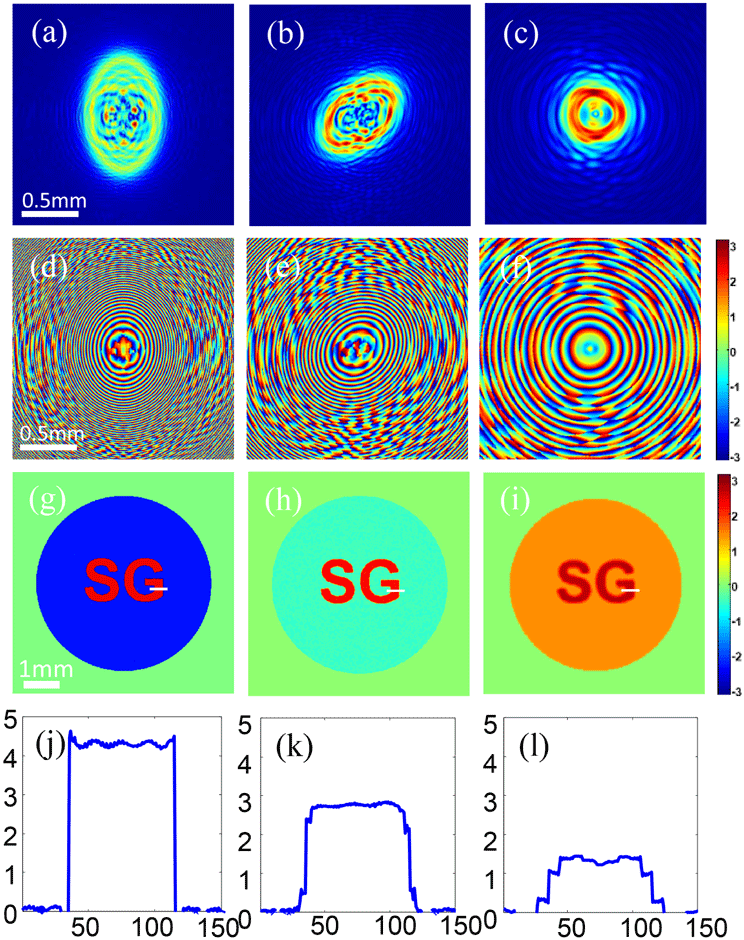
The spatial resolution and measurement accuracy of the proposed three-wavelength CMI approach were also studied. A phase resolution target with a structure similar to the common USAF 1951 pattern was used. However, in this case, each tiny bar was evaporated silicon on a quartz plate and the transmitted phase retardation was previously calibrated using an interferometer. Thus, this kind of phase resolution target can be used to simultaneously check the capability of three-wavelength CMI in terms of spatial resolution and phase measurement accuracy. In the experiments, one diffraction pattern
![]() $I_{1}$
was recorded to measure the background phase distribution of the three wavelengths using the proposed method, before the phase resolution target was introduced. After the phase resolution target was placed in the optical path, another diffraction pattern
$I_{1}$
was recorded to measure the background phase distribution of the three wavelengths using the proposed method, before the phase resolution target was introduced. After the phase resolution target was placed in the optical path, another diffraction pattern
![]() $I_{2}$
was recorded to reconstruct the transmitted complex amplitude for the three wavelengths. The phase retardation of the phase resolution target can be obtained for each wavelength by subtracting the corresponding phase for two measurements. The utilized phase resolution target has a designed phase delay of
$I_{2}$
was recorded to reconstruct the transmitted complex amplitude for the three wavelengths. The phase retardation of the phase resolution target can be obtained for each wavelength by subtracting the corresponding phase for two measurements. The utilized phase resolution target has a designed phase delay of
![]() $0.2\unicode[STIX]{x1D706}$
for 1053 nm. Therefore, the phase delays are 3.7699, 2.5133 and 1.2566 for 351 nm, 526.5 nm and 1053 nm, respectively. In addition, since the resolution achieved at 1053 nm was three times worse than that at 351 nm for the same optical setup, the image obtained at 1053 nm is obviously dim and blurry in the reconstructed phase images of the phase resolution target shown in Figures 15(a)–15(c). The dotted red rectangle in Figures 15(a)–15(c) indicates that the achieved resolution limits are
$0.2\unicode[STIX]{x1D706}$
for 1053 nm. Therefore, the phase delays are 3.7699, 2.5133 and 1.2566 for 351 nm, 526.5 nm and 1053 nm, respectively. In addition, since the resolution achieved at 1053 nm was three times worse than that at 351 nm for the same optical setup, the image obtained at 1053 nm is obviously dim and blurry in the reconstructed phase images of the phase resolution target shown in Figures 15(a)–15(c). The dotted red rectangle in Figures 15(a)–15(c) indicates that the achieved resolution limits are
![]() $49.61~\unicode[STIX]{x03BC}\text{m}$
(Group 3, Element 3) for 351 nm,
$49.61~\unicode[STIX]{x03BC}\text{m}$
(Group 3, Element 3) for 351 nm,
![]() $70.15~\unicode[STIX]{x03BC}\text{m}$
(Group 2, Element 6) for 526.5 nm and
$70.15~\unicode[STIX]{x03BC}\text{m}$
(Group 2, Element 6) for 526.5 nm and
![]() $125~\unicode[STIX]{x03BC}\text{m}$
(Group 2, Element 1) for 1053 nm. The phase values along the solid red lines in Figures 15(a)–15(c) are plotted in Figures 15(d)–15(f) so that they can be more easily examined. It can be seen that they are very close to the theoretically designed values.
$125~\unicode[STIX]{x03BC}\text{m}$
(Group 2, Element 1) for 1053 nm. The phase values along the solid red lines in Figures 15(a)–15(c) are plotted in Figures 15(d)–15(f) so that they can be more easily examined. It can be seen that they are very close to the theoretically designed values.

Figure 15. Reconstructed results for a step phase plate: (a) 351 nm, (b) 526.5 nm, (c) 1053 nm. (d)–(f) plot the red solid line in (a)–(c), respectively.
4 Conclusion
To address the problem of simultaneously measuring the fundamental, second and third harmonics behind FOAs for high-power laser facilities, a three-wavelength CMI-based online diagnosis technique was proposed. A specially designed modulator was adopted to scatter the hybrid laser beam and produce diffraction patterns, and a conventional CMI algorithm was modified to simultaneously reconstruct the complex amplitude of each wavelength. The feasibility of this proposed method was demonstrated both numerically and experimentally. The spatial resolution and measurement accuracy can approach
![]() $125~\unicode[STIX]{x03BC}\text{m}$
and 0.2 wavelengths, respectively, for 1053 nm. Due to its advantages, which include a compact structure, convenient operation, high resolution, and high accuracy, this proposed approach can potentially be utilized as a tool for online diagnosis of high-power beams behind FOAs, which is one of the most difficult longstanding problems in the field of high-power lasers.
$125~\unicode[STIX]{x03BC}\text{m}$
and 0.2 wavelengths, respectively, for 1053 nm. Due to its advantages, which include a compact structure, convenient operation, high resolution, and high accuracy, this proposed approach can potentially be utilized as a tool for online diagnosis of high-power beams behind FOAs, which is one of the most difficult longstanding problems in the field of high-power lasers.
Acknowledgements
This work is supported by the National Natural Science Foundation of China (NSFC) (Nos. 61827816, 61675215, and 11875308), the Scientific Instrument Developing Project of the Chinese Academy of Sciences (No. YJKYYQ20180024) and the Shanghai Sailing Program (No. 18YF1426600).
Supplementary movie
Supplementary movie is available at https://doi.org/10.1017/hpl.2019.26.