1. Introduction
The general physics of the Velocity Interferometer System for Any Reflector (VISAR)[Reference Barker and Hollenbach1–Reference Lemke, Knudson and Davis3] system, which we assume for this paper to be kinetic pressure driven, can be easily illustrated as in Figure 1. In this system, a time-dependent pressure ![]() $P(t)$ is applied to the left-hand side (LHS) of a thin (100–
$P(t)$ is applied to the left-hand side (LHS) of a thin (100–![]() $1000~{\rm\mu}\text{m}$) piece of metal called a VISAR flyer. This pressure results in stress wave propagation through the flyer and, eventually, motion of the right-hand side (RHS) surface of the flyer plate. A laser beam is reflected off the RHS, and the velocity
$1000~{\rm\mu}\text{m}$) piece of metal called a VISAR flyer. This pressure results in stress wave propagation through the flyer and, eventually, motion of the right-hand side (RHS) surface of the flyer plate. A laser beam is reflected off the RHS, and the velocity ![]() $\vec{v}$ of the RHS is inferred by means of an interferometry system. Since the properties of real materials obey an equation of state (EOS), one expects that there will be effects, such as compressibility and time delay (due to wave propagation with finite sound speed), which can play a significant role in determining the velocity of the RHS. By modeling the dynamics of the flyer, one can unfold the measured velocity response and infer the time-dependent pressure drive.
$\vec{v}$ of the RHS is inferred by means of an interferometry system. Since the properties of real materials obey an equation of state (EOS), one expects that there will be effects, such as compressibility and time delay (due to wave propagation with finite sound speed), which can play a significant role in determining the velocity of the RHS. By modeling the dynamics of the flyer, one can unfold the measured velocity response and infer the time-dependent pressure drive.
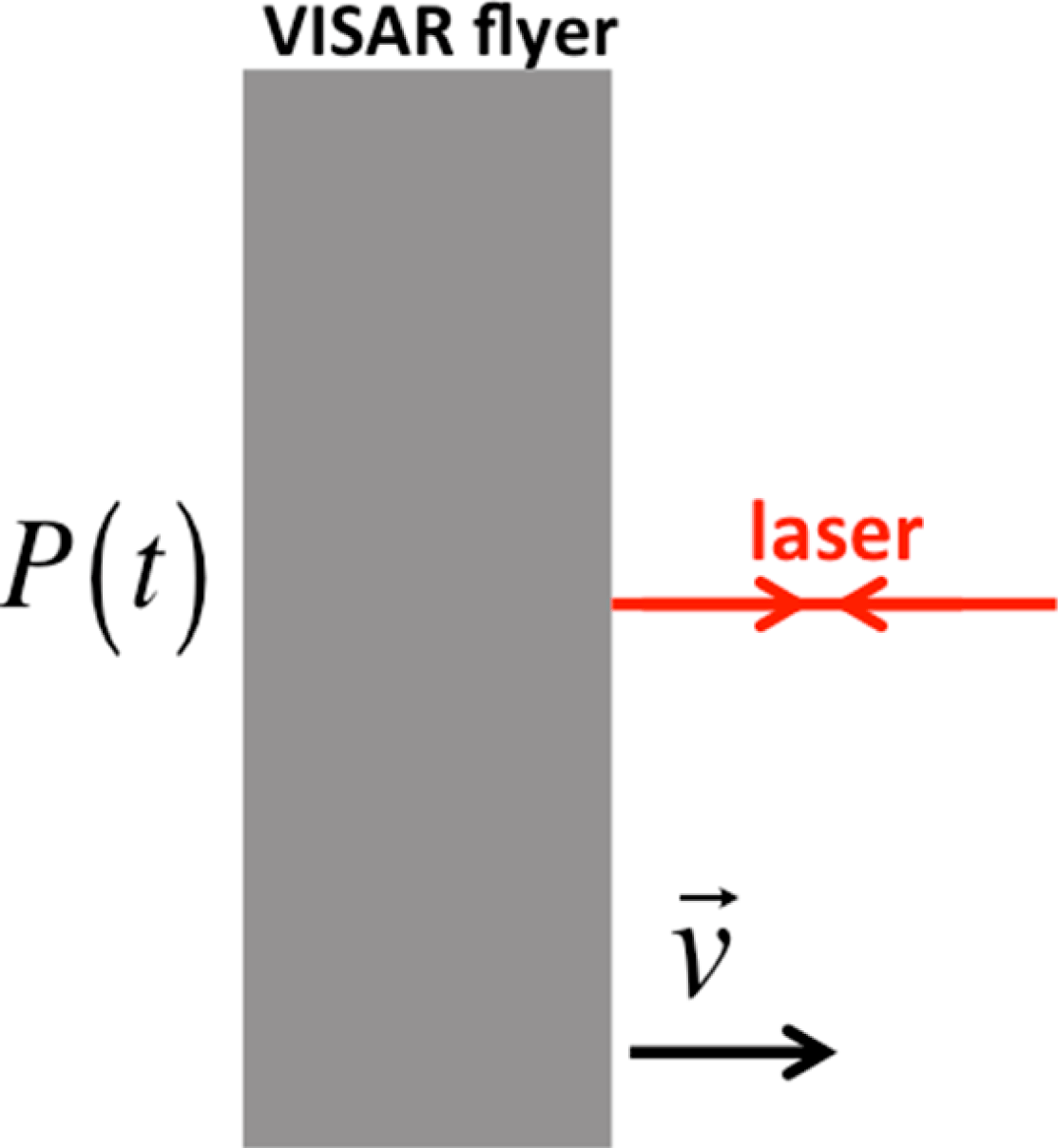
Figure 1. Illustration of the kinetic pressure driven VISAR diagnostic.
At Sandia National Laboratories, codes such as ALEGRA[Reference Robinson, Brunner, Carroll, Drake, Garasi, Gardiner, Haill, Hanshaw, Hensinger, Labreche, Lemke, Love, Luchini, Mosso, Niederhaus, Ober, Petney, Rider, Scovazzi, Strack, Summers, Trucano, Weirs, Wong and Voth4], HYDRA[Reference Marinak, Kerbel, Gentile, Jones, Munro, Pollaine, Dittrich and Haan5] and LASNEX[Reference Zimmermann and Kruer6] are commonly utilized in modeling the hydrodynamics (HD) of the VISAR flyer. These codes enable the user to produce a velocity output for a given pressure drive. To unfold the actual pressure incident on the VISAR flyer, a forward iterative process is used to match the simulated flyer velocity with the measured velocity. This pressure unfold is time consuming, i.e. it often requires many forward simulations to achieve a desired unfold accuracy, and still requires an initial ‘guess’ at the pressure drive to initiate the process. Another unfortunate aspect of the unfold process is that it may not have a unique solution, thereby limiting the accuracy of the unfold, since it falls into the general class of inverse problems. For example, one may find that a number of slightly different unfolded drives may produce similar velocity outputs. This can lead to an approximation of the uncertainty in an unfold candidate, assuming that there are no systematic errors associated with the VISAR velocity measurement. Let us say, after performing the unfold process a number of times, we arrive at a reasonable pressure drive candidate that results in a ![]() $\pm 5\%$ variation in the velocity output compared to the measured velocity. One can then roughly estimate that the uncertainty of the drive pressure is also
$\pm 5\%$ variation in the velocity output compared to the measured velocity. One can then roughly estimate that the uncertainty of the drive pressure is also ![]() $\pm 5\%$. This follows from the important property that, in the small pressure drive limit,
$\pm 5\%$. This follows from the important property that, in the small pressure drive limit, ![]() $P\ll {\it\rho}_{0}c_{0}^{2}$, where
$P\ll {\it\rho}_{0}c_{0}^{2}$, where ![]() ${\it\rho}_{0}$ is the initial mass density of the flyer and
${\it\rho}_{0}$ is the initial mass density of the flyer and ![]() $c_{0}$ is the material sound speed in the limit of zero pressure and zero temperature, the metal flyer can be modeled elastically, and hence the velocity output is proportional to the pressure. We will illustrate this property in the next section.
$c_{0}$ is the material sound speed in the limit of zero pressure and zero temperature, the metal flyer can be modeled elastically, and hence the velocity output is proportional to the pressure. We will illustrate this property in the next section.
The initial guess pressure function is a critical component to the unfold process. Specifically, one often finds that the initial unfold needs to be ‘sufficiently close’ to the final answer in order for the iterative process to actually converge in a timely fashion. By ‘sufficiently close’, we mean that the initial drive candidate should have roughly a similar maximum/minimum magnitude, and a similar shape as a function of time compared to the correct solution. If an auxiliary measurement of the pressure drive exists, then this would often suffice as an initial drive candidate. However, in some experiments it may not be possible to make an auxiliary measurement, in which case it would be necessary to find an alternative method for initializing the unfold process. A specific example of an auxiliary measurement is the use of B-dot probes to measure current through a load[Reference Martin, Lemke, McBride, Davis, Dolan, Knudson, Cochrane, Sinars, Smith, Savage, Stygar, Killebrew, Flicker and Herrmann7], and hence magnetic pressure on a VISAR flyer near the load, on the Sandia National Laboratory Z machine[Reference Matzen, Sweeney, Adams, Asay, Bailey, Bennett, Bliss, Bloomquist, Brunner, Campbell, Chandler, Coverdale, Cuneo, Davis, Deeney, Desjarlais, Donovan, Garasi, Haill, Hall, Hanson, Hurst, Jones, Knudson, Leeper, Lemke, Mazarakis, McDaniel, Mehlhorn, Nash, Olson, Porter, Rambo, Rosenthal, Rochau, Ruggles, Ruiz, Sanford, Seamen, Sinars, Slutz, Smith, Struve, Stygar, Vesey, Weinbrecht, Wenger and Yu8] during pulsed-power experiments. It is often found, however, that the B-dot probes work well in the low-current regime of the pulse, but may fail at or near peak current. Hence, the B-dots can provide an accurate initial guess of the magnetic pressure in the low-pressure regime, but an unfolded load VISAR measurement would provide a more accurate representation of the pressure at higher currents. In certain cases, such as in recent laser blast wave experiments in support of the MagLIF project[Reference Slutz, Herrmann, Vesey, Sefkow, Sinars, Rovang, Peterson and Cuneo9], it may be possible to simulate the pressure generated by the blast wave due to a laser pulse entirely using a HD code, such as HYDRA. This pressure drive function could then be used as a candidate drive in the unfold process. We should note that other methods for unfolding VISAR data have been developed. For example, a Lagrangian-style backwards spatial integration method[Reference Hayes10] was developed for investigating dynamic materials experiments at Sandia National Laboratories. In contrast to this method, our unfold method utilizes physics at the boundaries of the flyer without resorting to extensive simulations of the internal flyer physics.
The remainder of this paper describes a technique that we developed for producing the initial guess function for the pressure drive. The method relies on both analytical techniques, as well as implementation of well-known EOS tables, such as the SESAME[Reference Holian11] table. This method proves to be very quick, e.g. producing unfolds for our laser blast wave experiments in under 30 s. Moreover, the method produces a pressure drive that yields excellent agreement between the actual VISAR data and the simulated VISAR velocity when modeled with a HD simulation code. The difference between the simulated velocity and the data is typically ![]() ${\sim}1\%$ (velocity difference/maximum VISAR velocity) for most of the key components of our datasets. Larger errors,
${\sim}1\%$ (velocity difference/maximum VISAR velocity) for most of the key components of our datasets. Larger errors, ![]() ${\sim}5\%{-}10\%$, become present due to the difficulty in our method in resolving density variations due to reflections at the VISAR surface, as well as the physics of the release wave in the presence of very strong pressure shocks. Despite these issues, this method has proven to be extremely effective for unfolding kinetic pressure driven VISAR unfolds. One should note that, in practice, a 1% error for a pressure function using an iterative method is often times the best that is achievable. The reason for this is that the unfold process can be extremely nonlinear, i.e. a small change in the pressure drive may lead to a not so small change in VISAR velocity, particularly in the presence of a pressure shock. In certain cases, our method is effective enough to completely avoid employing iterative methods afterwards, and use the initial pressure guess as the unfold itself.
${\sim}5\%{-}10\%$, become present due to the difficulty in our method in resolving density variations due to reflections at the VISAR surface, as well as the physics of the release wave in the presence of very strong pressure shocks. Despite these issues, this method has proven to be extremely effective for unfolding kinetic pressure driven VISAR unfolds. One should note that, in practice, a 1% error for a pressure function using an iterative method is often times the best that is achievable. The reason for this is that the unfold process can be extremely nonlinear, i.e. a small change in the pressure drive may lead to a not so small change in VISAR velocity, particularly in the presence of a pressure shock. In certain cases, our method is effective enough to completely avoid employing iterative methods afterwards, and use the initial pressure guess as the unfold itself.
The VISAR unfold method is broken into two parts, which are separately applicable in the ‘low-pressure’ and ‘high-pressure’ regimes. The ‘low-pressure’ part utilizes a many-body coupled harmonic oscillator model for the metal VISAR flyer to predict the VISAR velocity response due to a time-dependent pressure. The ‘high-pressure’ part utilizes realistic EOS tables, such as the SESAME tables, to predict the VISAR response due to the time-dependent velocity. As we shall see, both parts of the method yield excellent VISAR unfold predictions in the different pressure response regimes that can be ‘spliced’ together to form a very accurate VISAR unfold of the pressure.
2. ‘Low-pressure’ coupled harmonic oscillator model
Coupled harmonic oscillator models in solid-state physics are well known, and were initially developed by Einstein[Reference Einstein12], Debye[Reference Debye13] and Gruneisen[Reference Gruneisen14]. In the ‘low-pressure’ limit, in which the density of the VISAR flyer, as well as its sound speed remain constant, this model can be very effective. We now illustrate how the coupled harmonic oscillator model can be applied to the VISAR unfold process.
Suppose that a large metal flyer plate of total mass ![]() $M$ and thickness
$M$ and thickness ![]() $L$ is divided into
$L$ is divided into ![]() $N$ equal slices, each of mass
$N$ equal slices, each of mass ![]() $m=M/N$ and with centers spaced a distance
$m=M/N$ and with centers spaced a distance ![]() $l=L/N$. We label the center location, velocity and acceleration of the
$l=L/N$. We label the center location, velocity and acceleration of the ![]() $i\text{th}$ slice as
$i\text{th}$ slice as ![]() $x_{i},v_{i}$ and
$x_{i},v_{i}$ and ![]() $a_{i}$, respectively. In our system, the
$a_{i}$, respectively. In our system, the ![]() $i=1$ slice corresponds to the LHS of the system shown in Figure 1 (where the pressure is applied) and
$i=1$ slice corresponds to the LHS of the system shown in Figure 1 (where the pressure is applied) and ![]() $i=N$ corresponds to the RHS of the system (where the VISAR measurement is made). We assume that the
$i=N$ corresponds to the RHS of the system (where the VISAR measurement is made). We assume that the ![]() $i=1$ slice has a time-dependent force
$i=1$ slice has a time-dependent force ![]() $F(t)$ being applied to it, and that each slice is interacting with its neighboring slices via a harmonic potential with spring constant
$F(t)$ being applied to it, and that each slice is interacting with its neighboring slices via a harmonic potential with spring constant ![]() $k$, or equivalently a characteristic frequency
$k$, or equivalently a characteristic frequency ![]() ${\it\omega}=\sqrt{k/m}$. Newton’s laws yield
${\it\omega}=\sqrt{k/m}$. Newton’s laws yield
 $$\begin{eqnarray}\begin{array}{@{}c@{}}\displaystyle m\frac{d^{2}x_{1}}{dt^{2}}=-k(x_{1}-x_{2}+l)+F(t)\\ \displaystyle m\frac{d^{2}x_{i}}{dt^{2}}=-k(x_{i-1}-x_{i+1}+2l)\quad \text{for }2<i<N\\ \displaystyle m\frac{d^{2}x_{N}}{dt^{2}}=-k(x_{N}-x_{N-1}-l).\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}c@{}}\displaystyle m\frac{d^{2}x_{1}}{dt^{2}}=-k(x_{1}-x_{2}+l)+F(t)\\ \displaystyle m\frac{d^{2}x_{i}}{dt^{2}}=-k(x_{i-1}-x_{i+1}+2l)\quad \text{for }2<i<N\\ \displaystyle m\frac{d^{2}x_{N}}{dt^{2}}=-k(x_{N}-x_{N-1}-l).\end{array}\end{eqnarray}$$ Since we are modeling the internal motion of a continuous solid flyer, we are obviously only interested in the limit that ![]() $N\rightarrow \infty$. It is readily straightforward to reduce this set of equations into one single ordinary differential equation for
$N\rightarrow \infty$. It is readily straightforward to reduce this set of equations into one single ordinary differential equation for ![]() $x_{N}$, or equivalently
$x_{N}$, or equivalently ![]() $a_{N}$, in terms of
$a_{N}$, in terms of ![]() $F$. In the large-
$F$. In the large-![]() $N$ limit, we let
$N$ limit, we let ![]() $a_{N}\rightarrow a_{\text{RHS}}$, where the subscript ‘RHS’ denotes the RHS of the flyer where the VISAR measurement is made. The final differential equation for
$a_{N}\rightarrow a_{\text{RHS}}$, where the subscript ‘RHS’ denotes the RHS of the flyer where the VISAR measurement is made. The final differential equation for ![]() $a_{N}\rightarrow a_{\text{RHS}}$ becomes
$a_{N}\rightarrow a_{\text{RHS}}$ becomes
 $$\begin{eqnarray}\displaystyle \frac{F}{M} & = & \displaystyle a_{\text{RHS}}+\frac{1}{3!\tilde{{\it\omega}}^{2}}\frac{d^{2}a_{\text{RHS}}}{dt^{2}}+\frac{1}{5!\tilde{{\it\omega}}^{4}}\frac{d^{4}a_{\text{RHS}}}{dt^{4}}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{7!\tilde{{\it\omega}}^{6}}\frac{d^{6}a_{\text{RHS}}}{dt^{6}}+\cdots \nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{n=0}^{\infty }\frac{1}{(2n+1)!\tilde{{\it\omega}}^{2n}}\frac{d^{2n}a_{\text{RHS}}}{dt^{2n}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{F}{M} & = & \displaystyle a_{\text{RHS}}+\frac{1}{3!\tilde{{\it\omega}}^{2}}\frac{d^{2}a_{\text{RHS}}}{dt^{2}}+\frac{1}{5!\tilde{{\it\omega}}^{4}}\frac{d^{4}a_{\text{RHS}}}{dt^{4}}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{7!\tilde{{\it\omega}}^{6}}\frac{d^{6}a_{\text{RHS}}}{dt^{6}}+\cdots \nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{n=0}^{\infty }\frac{1}{(2n+1)!\tilde{{\it\omega}}^{2n}}\frac{d^{2n}a_{\text{RHS}}}{dt^{2n}},\end{eqnarray}$$ where ![]() $\tilde{{\it\omega}}={\it\omega}/N$ is a renormalized characteristic frequency. We should note that the authors derived the coefficients for Equation (2) by numerically solving the coefficients for sequentially larger finite-
$\tilde{{\it\omega}}={\it\omega}/N$ is a renormalized characteristic frequency. We should note that the authors derived the coefficients for Equation (2) by numerically solving the coefficients for sequentially larger finite-![]() $N$ systems, and found that the coefficients approached the values in Equation (2) as
$N$ systems, and found that the coefficients approached the values in Equation (2) as ![]() $N\rightarrow \infty$. Equation (2) can be written into a simple expression for the RHS velocity as
$N\rightarrow \infty$. Equation (2) can be written into a simple expression for the RHS velocity as
 $$\begin{eqnarray}\displaystyle \frac{F}{M} & = & \displaystyle \mathop{\sum }_{n=0}^{\infty }\frac{1}{(2n+1)!\tilde{{\it\omega}}^{2n}}\frac{d^{2n+1}v_{\text{RHS}}}{dt^{2n+1}}\nonumber\\ \displaystyle & = & \displaystyle \frac{\tilde{{\it\omega}}}{2}(v_{\text{RHS}}(t+1/\tilde{{\it\omega}})-v_{\text{RHS}}(t-1/\tilde{{\it\omega}})).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{F}{M} & = & \displaystyle \mathop{\sum }_{n=0}^{\infty }\frac{1}{(2n+1)!\tilde{{\it\omega}}^{2n}}\frac{d^{2n+1}v_{\text{RHS}}}{dt^{2n+1}}\nonumber\\ \displaystyle & = & \displaystyle \frac{\tilde{{\it\omega}}}{2}(v_{\text{RHS}}(t+1/\tilde{{\it\omega}})-v_{\text{RHS}}(t-1/\tilde{{\it\omega}})).\end{eqnarray}$$ The final expression is immediately found through Taylor series expansions. Therefore, the velocity of the RHS at any time ![]() $t$ is equal to the velocity at an earlier time
$t$ is equal to the velocity at an earlier time ![]() $t-2/\tilde{{\it\omega}}$ plus a term that is linearly proportional to the force applied to the LHS at an earlier time
$t-2/\tilde{{\it\omega}}$ plus a term that is linearly proportional to the force applied to the LHS at an earlier time ![]() $t-1/\tilde{{\it\omega}}$. In the absence of a viscoelastic strength model, any longitudinal pressure pulse will propagate through the flyer with a sound speed
$t-1/\tilde{{\it\omega}}$. In the absence of a viscoelastic strength model, any longitudinal pressure pulse will propagate through the flyer with a sound speed ![]() $c$, which we assume to be constant. Hence, the renormalized frequency can be written as
$c$, which we assume to be constant. Hence, the renormalized frequency can be written as ![]() $\tilde{{\it\omega}}=c/L$. The total mass can be written as
$\tilde{{\it\omega}}=c/L$. The total mass can be written as ![]() $M={\it\rho}_{0}AL$ and the pressure is
$M={\it\rho}_{0}AL$ and the pressure is ![]() $P=F/A$, where
$P=F/A$, where ![]() $A$ is the surface area of the flyer. Equation (3) can then be rewritten as
$A$ is the surface area of the flyer. Equation (3) can then be rewritten as
 $$\begin{eqnarray}\displaystyle v_{\text{RHS}}(t) & = & \displaystyle v_{\text{RHS}}(t-2L/c)+\frac{2P(t-L/c)}{{\it\rho}_{0}c}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{n=0}^{\infty }\frac{2P(t-(2n+1)L/c)}{{\it\rho}_{0}c}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle v_{\text{RHS}}(t) & = & \displaystyle v_{\text{RHS}}(t-2L/c)+\frac{2P(t-L/c)}{{\it\rho}_{0}c}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{n=0}^{\infty }\frac{2P(t-(2n+1)L/c)}{{\it\rho}_{0}c}.\end{eqnarray}$$ We should note that, since ![]() $\tilde{{\it\omega}}$ is assumed to be constant in the model, both
$\tilde{{\it\omega}}$ is assumed to be constant in the model, both ![]() $c$ and
$c$ and ![]() $L$ are also assumed to be constant. For real materials that are undergoing a pressure drive, there will always be a change in density and, hence, a change in
$L$ are also assumed to be constant. For real materials that are undergoing a pressure drive, there will always be a change in density and, hence, a change in ![]() $L$. One can estimate the size of the density perturbation using the above velocity equation and the continuity equation. The density perturbation will be of the order of
$L$. One can estimate the size of the density perturbation using the above velocity equation and the continuity equation. The density perturbation will be of the order of ![]() ${\it\delta}{\it\rho}\sim P/c$. Additionally, since the speed of sound for real materials is a function of density and temperature, there will also be a change in
${\it\delta}{\it\rho}\sim P/c$. Additionally, since the speed of sound for real materials is a function of density and temperature, there will also be a change in ![]() $c$. In order to justify our fixed density and fixed sound speed model, it is sufficient to ensure that the density perturbation is small compared to the initial density when the pressure is zero. This ‘low pressure’ is achieved when the pressure satisfies
$c$. In order to justify our fixed density and fixed sound speed model, it is sufficient to ensure that the density perturbation is small compared to the initial density when the pressure is zero. This ‘low pressure’ is achieved when the pressure satisfies ![]() $P\ll {\it\rho}_{0}c_{0}^{2}$.
$P\ll {\it\rho}_{0}c_{0}^{2}$.
We now show an example in order to illustrate the utility of Equation (4) by comparing its prediction to a full hydrodynamic simulation using the arbitrary-Lagrangian–Eulerian multimaterial code ALEGRA developed at Sandia National Laboratories. In this example, we use a time-dependent pressure, shown in Figure 2(a), to drive a ![]() $L=200~{\rm\mu}\text{m}$ thick aluminum VISAR flyer. In order to demonstrate the effectiveness of Equation (4), the pressure profile that we use is derived from actual VISAR velocity data (up to a scaling factor) from experiments at Sandia studying the effects of a blast wave driven by the deposition of laser energy (2 kJ total) into an underdense gas in a MagLIF target[Reference Sinars15]. The code uses the SESAME 3700 EOS table and the Lee–More–Desjarlais (LMD)[Reference Desjarlais16] model for computing conductivities. The ALEGRA simulation is run in a 1D Lagrangian mode, and the flyer is resolved with 1000 cells throughout the bulk of the flyer. In these simulations, the density and sound speed of the aluminum are given by
$L=200~{\rm\mu}\text{m}$ thick aluminum VISAR flyer. In order to demonstrate the effectiveness of Equation (4), the pressure profile that we use is derived from actual VISAR velocity data (up to a scaling factor) from experiments at Sandia studying the effects of a blast wave driven by the deposition of laser energy (2 kJ total) into an underdense gas in a MagLIF target[Reference Sinars15]. The code uses the SESAME 3700 EOS table and the Lee–More–Desjarlais (LMD)[Reference Desjarlais16] model for computing conductivities. The ALEGRA simulation is run in a 1D Lagrangian mode, and the flyer is resolved with 1000 cells throughout the bulk of the flyer. In these simulations, the density and sound speed of the aluminum are given by ![]() ${\it\rho}_{0}=2700~\text{kg}~\text{m}^{-3}$ and
${\it\rho}_{0}=2700~\text{kg}~\text{m}^{-3}$ and ![]() $c=5216~\text{m}~\text{s}^{-1}$, and material strength effects have been turned off. For aluminum, our ‘low-pressure’ criterion yields
$c=5216~\text{m}~\text{s}^{-1}$, and material strength effects have been turned off. For aluminum, our ‘low-pressure’ criterion yields ![]() $P\ll 73~\text{GPa}$, and this is satisfied within the simulation in which
$P\ll 73~\text{GPa}$, and this is satisfied within the simulation in which ![]() $P<500~\text{kPa}$. In Figure 2(b), we show the excellent agreement between ALEGRA (red) and the velocity prediction for the coupled harmonic oscillator model in Equation (4) (green). It is immediately obvious that in this ‘low-pressure’ regime, the coupled harmonic oscillator model is extremely powerful, and can be used to accurately predict the VISAR velocity response due to a time-dependent pressure drive.
$P<500~\text{kPa}$. In Figure 2(b), we show the excellent agreement between ALEGRA (red) and the velocity prediction for the coupled harmonic oscillator model in Equation (4) (green). It is immediately obvious that in this ‘low-pressure’ regime, the coupled harmonic oscillator model is extremely powerful, and can be used to accurately predict the VISAR velocity response due to a time-dependent pressure drive.
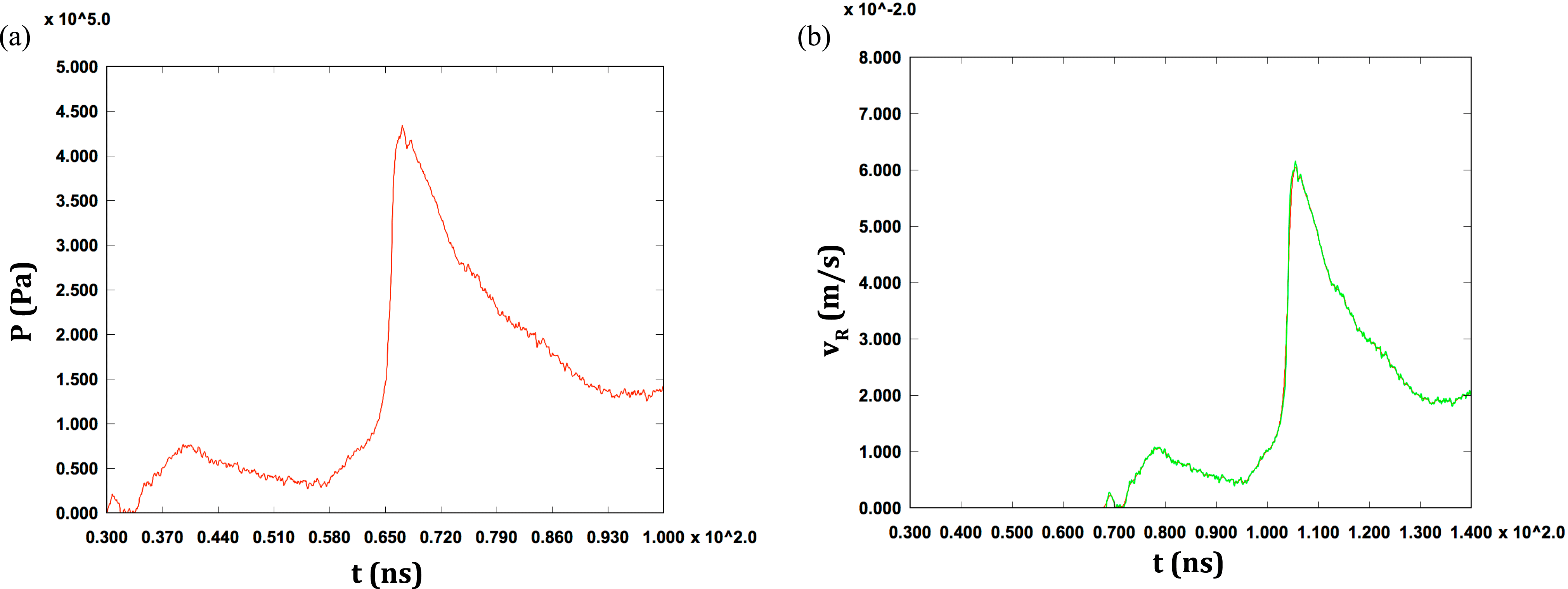
Figure 2. (a) Example of a low-pressure drive. (b) The RHS velocity for the low-pressure drive computed by ALEGRA (red) and by Equation (4) (green).

Figure 3. (a) Example of a high-pressure drive. (b) The RHS velocity for the high-pressure drive computed by ALEGRA (red) and by Equation (4) (green).
In order to illustrate how the coupled harmonic oscillator model breaks down, suppose that we take an identical pressure drive and multiply it by ![]() $10^{\text{4}}$, so that the maximum pressure is of the order of 5 GPa, as shown in Figure 3(a). Figure 3(b) shows a comparison of the ALEGRA simulation (red) and the harmonic oscillator model (green). A few things are immediately apparent from Figure 3(b). First, there is a time shift between the velocity traces, which is small for the lower velocities that correspond to lower pressures, and becomes more significant for high velocities that correspond to high pressure. The time shift is due to two effects: (1) the VISAR thickness contracts (smaller
$10^{\text{4}}$, so that the maximum pressure is of the order of 5 GPa, as shown in Figure 3(a). Figure 3(b) shows a comparison of the ALEGRA simulation (red) and the harmonic oscillator model (green). A few things are immediately apparent from Figure 3(b). First, there is a time shift between the velocity traces, which is small for the lower velocities that correspond to lower pressures, and becomes more significant for high velocities that correspond to high pressure. The time shift is due to two effects: (1) the VISAR thickness contracts (smaller ![]() $L$) for higher-pressure drives and (2) the speed of sound is a function of density. For aluminum, as is true for most solids, the speed of sound increases as the density increases (higher
$L$) for higher-pressure drives and (2) the speed of sound is a function of density. For aluminum, as is true for most solids, the speed of sound increases as the density increases (higher ![]() $c$). Both of these effects contribute to a smaller time delay in the velocity response. However, despite the small time shift in the low-velocity regime, one still finds very good agreement between the two results in the low-velocity regime, particularly when the pressure is <1 GPa for aluminum VISAR flyers. The other effect is that the velocity predicted by this model is significantly higher than the ALEGRA simulation result. This effect is due to momentum conservation. In the coupled harmonic oscillator model, the density was assumed to be constant, when in reality the density is increasing under compression. As momentum propagates through the flyer from the LHS to the RHS, a local increase in density would necessarily be accompanied by a local decrease in velocity, which would not be seen in the oscillator model.
$c$). Both of these effects contribute to a smaller time delay in the velocity response. However, despite the small time shift in the low-velocity regime, one still finds very good agreement between the two results in the low-velocity regime, particularly when the pressure is <1 GPa for aluminum VISAR flyers. The other effect is that the velocity predicted by this model is significantly higher than the ALEGRA simulation result. This effect is due to momentum conservation. In the coupled harmonic oscillator model, the density was assumed to be constant, when in reality the density is increasing under compression. As momentum propagates through the flyer from the LHS to the RHS, a local increase in density would necessarily be accompanied by a local decrease in velocity, which would not be seen in the oscillator model.
For our laser driven blast wave experiments at Sandia, typical pressure drives will have maxima in the 1–10 GPa regime. So we expect that the coupled harmonic oscillator model would give accurate results in regimes corresponding to low pressure (often times in the ‘initial foot’ of the pressure drive), but would need to be modified to incorporate higher-pressure drives.
3. ‘High-pressure’ model
In this section, we show an improved model, which accounts for the changes in thickness of the VISAR flyer, as well as the density dependence of the material sound speed. However, we still limit our discussion to the constant temperature approximation, which in our case corresponds to room temperature at ![]() $T=298~\text{K}$. For the laser blast wave experiments, ALEGRA simulations indicate that the VISAR flyer temperature (ignoring radiation surface ablation effects) will vary by less than 100 K throughout the spatial extent of the flyer during 100 ns of the laser blast wave. This relatively small change in temperature results in little change of the pressure, as well as the sound speed. This approximation significantly simplifies the unfold model. Although the constant temperature approximation works very well in the pressure drive regime of
$T=298~\text{K}$. For the laser blast wave experiments, ALEGRA simulations indicate that the VISAR flyer temperature (ignoring radiation surface ablation effects) will vary by less than 100 K throughout the spatial extent of the flyer during 100 ns of the laser blast wave. This relatively small change in temperature results in little change of the pressure, as well as the sound speed. This approximation significantly simplifies the unfold model. Although the constant temperature approximation works very well in the pressure drive regime of ![]() ${<}10~\text{GPa}$, it is not immediately clear how high a pressure drive is possible before this approximation, and hence the present unfold process, yield significant errors. For large pressures, which can result in significant changes in the flyer temperature, full simulations of the flyer may be required using a code such as ALEGRA.
${<}10~\text{GPa}$, it is not immediately clear how high a pressure drive is possible before this approximation, and hence the present unfold process, yield significant errors. For large pressures, which can result in significant changes in the flyer temperature, full simulations of the flyer may be required using a code such as ALEGRA.
We make an additional simplification by ignoring the effects of density and pressure reflections in the system. The main drawback of this approximation is that it limits the length of time over which the unfold can be applied, since reflections that make it back to the LHS can affect the density along with the external pressure. If one knows approximately the characteristic time of the pressure response, then the VISAR flyer can be made sufficiently thick so as to reduce the effect of the reflections. Despite this additional assumption, we find that it still offers a useful unfold that is highly relevant for our experimental data.
The model utilizes mass and momentum conservation, as well as pressure boundary conditions applied at the LHS and RHS. In order to capture the correct physics of the density dependence of the sound speed within the flyer, it is necessary to incorporate well-known EOS tables, such as the SESAME tables. These tables provide material pressure as a function of density and temperature, i.e. ![]() $P({\it\rho},T)$, as well as the energy per mass
$P({\it\rho},T)$, as well as the energy per mass ![]() ${\it\varepsilon}({\it\rho},T)$, from which the sound speed can also be found
${\it\varepsilon}({\it\rho},T)$, from which the sound speed can also be found ![]() $c({\it\rho},T)$. However, because we are only considering a fixed temperature model at
$c({\it\rho},T)$. However, because we are only considering a fixed temperature model at ![]() $T=298~\text{K}$, our model uses constant temperature curves for pressure and sound speed at
$T=298~\text{K}$, our model uses constant temperature curves for pressure and sound speed at ![]() $T=298~\text{K}$, i.e.,
$T=298~\text{K}$, i.e., ![]() $P({\it\rho},T=298~\text{K})$ and
$P({\it\rho},T=298~\text{K})$ and ![]() $c({\it\rho},T=298~\text{K})$.
$c({\it\rho},T=298~\text{K})$.
Assume that the external pressure drive on the LHS is given by ![]() $P_{\text{ext}}(t)$. Since the pressure is continuous across the material surface then one immediately obtains the density on the LHS, namely
$P_{\text{ext}}(t)$. Since the pressure is continuous across the material surface then one immediately obtains the density on the LHS, namely
Between time ![]() $t_{2}$ and
$t_{2}$ and ![]() $t_{3}$, when the pressure has changed to
$t_{3}$, when the pressure has changed to ![]() $P_{2}$, one finds that the LHS density is
$P_{2}$, one finds that the LHS density is ![]() ${\it\rho}_{2}$. Again, momentum conservation yields the new speed of the LHS
${\it\rho}_{2}$. Again, momentum conservation yields the new speed of the LHS
At each pressure step, conservation of momentum can be applied and, after ![]() $n$ steps, we find
$n$ steps, we find
In the limit of infinitesimally small pressure changes, Equation (9) becomes differentials in ![]() $v$ and
$v$ and ![]() $P$, and one finds that
$P$, and one finds that
where the dependence of the LHS density on pressure is found from Equation (6). We should note that in deriving Equation (10) we have ignored the effect of reflections, which in general can affect the density at the LHS.
The next important component of this unfold is determining the time-delay factor, i.e. the time for a pressure drive at the LHS to be received at the RHS. Suppose that at time ![]() $t$ the density of the LHS due to the pressure drive is
$t$ the density of the LHS due to the pressure drive is ![]() ${\it\rho}_{\text{LHS}}(t)$. We know that this pressure signal will propagate with a speed
${\it\rho}_{\text{LHS}}(t)$. We know that this pressure signal will propagate with a speed ![]() $c({\it\rho}_{\text{LHS}})$ through the VISAR flyer. However, since the density has been increased from the initial density
$c({\it\rho}_{\text{LHS}})$ through the VISAR flyer. However, since the density has been increased from the initial density ![]() ${\it\rho}_{0}$ (accordingly the thickness has decreased from the original thickness of
${\it\rho}_{0}$ (accordingly the thickness has decreased from the original thickness of ![]() $L$), the propagation distance has decreased, leading to a reduction in the time delay. The total time-delay factor for the signal to reach the RHS starting from the LHS is
$L$), the propagation distance has decreased, leading to a reduction in the time delay. The total time-delay factor for the signal to reach the RHS starting from the LHS is ![]() $L{\it\rho}_{0}/c({\it\rho}_{\text{LHS}}){\it\rho}_{\text{LHS}}$.
$L{\it\rho}_{0}/c({\it\rho}_{\text{LHS}}){\it\rho}_{\text{LHS}}$.
Since there is no pressure being applied to the RHS, the density of the RHS must stay fixed at ![]() ${\it\rho}_{\text{RHS}}={\it\rho}_{0}$ for all time. The material velocity of the signal is given by
${\it\rho}_{\text{RHS}}={\it\rho}_{0}$ for all time. The material velocity of the signal is given by ![]() $v_{\text{LHS}}$. Since the signal is reflected at the RHS boundary with the density held constant, the velocity of the RHS must be twice that of the incoming velocity. The velocity response of the RHS or VISAR measurement due to the time-dependent pressure drive with appropriate time-delay factor is given by
$v_{\text{LHS}}$. Since the signal is reflected at the RHS boundary with the density held constant, the velocity of the RHS must be twice that of the incoming velocity. The velocity response of the RHS or VISAR measurement due to the time-dependent pressure drive with appropriate time-delay factor is given by
What we have just described is a method for inferring the velocity of a VISAR signal from a time-dependent pressure drive. However, for most of our experiments we are actually interested in the inverse problem of taking the measured VISAR velocity data and finding the pressure drive. Our method can be readily run in reverse to produce a VISAR unfold, in the following manner. Using Equations (10) and (11), we can relate the RHS VISAR velocity to an appropriately time-shifted LHS pressure drive, i.e.
 $$\begin{eqnarray}\displaystyle v_{\text{RHS}}(t) & = & \displaystyle \int _{0}^{P_{\text{ext}}\left(t-\frac{L{\it\rho}_{0}}{c({\it\rho}_{\text{LHS}}){\it\rho}_{\text{LHS}}}\right)}\frac{2\mathit{dP}}{{\it\rho}_{\text{LHS}}c({\it\rho}_{\text{LHS}})}\nonumber\\ \displaystyle & = & \displaystyle \int _{{\it\rho}_{0}}^{{\it\rho}_{\text{LHS}}\left(t-\frac{L{\it\rho}_{0}}{c({\it\rho}_{\text{LHS}}){\it\rho}_{\text{LHS}}}\right)}\frac{2c({\it\rho})d{\it\rho}}{{\it\rho}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle v_{\text{RHS}}(t) & = & \displaystyle \int _{0}^{P_{\text{ext}}\left(t-\frac{L{\it\rho}_{0}}{c({\it\rho}_{\text{LHS}}){\it\rho}_{\text{LHS}}}\right)}\frac{2\mathit{dP}}{{\it\rho}_{\text{LHS}}c({\it\rho}_{\text{LHS}})}\nonumber\\ \displaystyle & = & \displaystyle \int _{{\it\rho}_{0}}^{{\it\rho}_{\text{LHS}}\left(t-\frac{L{\it\rho}_{0}}{c({\it\rho}_{\text{LHS}}){\it\rho}_{\text{LHS}}}\right)}\frac{2c({\it\rho})d{\it\rho}}{{\it\rho}},\end{eqnarray}$$ where in Equation (12) we have used the relation ![]() $c^{2}=\mathit{dP}/d{\it\rho}$. For each time
$c^{2}=\mathit{dP}/d{\it\rho}$. For each time ![]() $t$, the integral in Equation (12) is performed numerically to determine the correct
$t$, the integral in Equation (12) is performed numerically to determine the correct ![]() ${\it\rho}_{\text{LHS}}$ and, hence, the
${\it\rho}_{\text{LHS}}$ and, hence, the ![]() $P_{\text{ext}}$ that produces the RHS VISAR velocity. This provides the correct time-shift factor for
$P_{\text{ext}}$ that produces the RHS VISAR velocity. This provides the correct time-shift factor for ![]() $P_{\text{ext}}$ as shown in the integrand of Equation (12). Hence from Equation (12), the RHS VISAR velocity immediately determines the desired pressure drive
$P_{\text{ext}}$ as shown in the integrand of Equation (12). Hence from Equation (12), the RHS VISAR velocity immediately determines the desired pressure drive ![]() $P_{\text{ext}}(t)$.
$P_{\text{ext}}(t)$.
As an aside, it is worth noting that in the limit of small pressure, Equation (12) recovers Equation (4) without the inclusion of reflections. In particular, ![]() ${\it\rho}_{\text{LHS}}\rightarrow {\it\rho}_{0}$ and
${\it\rho}_{\text{LHS}}\rightarrow {\it\rho}_{0}$ and ![]() $c({\it\rho}_{\text{LHS}})\rightarrow c$ (constant sound speed), so that Equation (12) becomes
$c({\it\rho}_{\text{LHS}})\rightarrow c$ (constant sound speed), so that Equation (12) becomes
4. Implementation of the unfold process
In this section, we show how we can use both the ‘high-pressure’ model in Equation (12), which implements realistic EOS tables and accounts for the changes in thickness and sound speed of the material, as well as the ‘low-pressure’ coupled oscillator model in Equation (4) to produce an accurate unfold of the pressure. An obvious question that one may ask is why should the coupled oscillator model be used at all, since Equation (12) should be applicable in both the high- and low-pressure regimes. The answer is that, in general, it can be challenging to interpolate the sound speed of the flyer as ![]() $P$ approaches zero for a given EOS table. This property is readily connected to the fact that the sound speed has a discontinuous derivative as
$P$ approaches zero for a given EOS table. This property is readily connected to the fact that the sound speed has a discontinuous derivative as ![]() $P$ approaches zero. However, since the low-pressure regime can be resolved using Equation (13), which is identical (without reflections) to the coupled oscillator result in Equation (4), then one can use the coupled oscillator result (or equivalently Equation (13)) to unfold the VISAR data in low-pressure regimes. This requires that we choose an appropriate velocity/drive pressure cutoff below which we use Equation (4) or (13) and above which we use Equation (12) to unfold the pressure. For aluminum, choosing a velocity cutoff to be
$P$ approaches zero. However, since the low-pressure regime can be resolved using Equation (13), which is identical (without reflections) to the coupled oscillator result in Equation (4), then one can use the coupled oscillator result (or equivalently Equation (13)) to unfold the VISAR data in low-pressure regimes. This requires that we choose an appropriate velocity/drive pressure cutoff below which we use Equation (4) or (13) and above which we use Equation (12) to unfold the pressure. For aluminum, choosing a velocity cutoff to be ![]() $100~\text{m}~\text{s}^{-1}$ and the associated pressure cutoff to be 0.7 GPa provides excellent results.
$100~\text{m}~\text{s}^{-1}$ and the associated pressure cutoff to be 0.7 GPa provides excellent results.

Figure 4. Schematic of the MagLIF laser blast wave experiment.
We illustrate this unfold process using actual data from a series of experiments, which investigated the properties of the laser blast wave found in the Sandia MagLIF experiment. In these experiments, a ![]() $200~{\rm\mu}\text{m}$ thick aluminum tube with an initial radius of 2.8 mm contains a
$200~{\rm\mu}\text{m}$ thick aluminum tube with an initial radius of 2.8 mm contains a ![]() $\text{D}_{\text{2}}$ gas fill at 57 psi. A 2 kJ laser pulse from the Sandia Z-Beamlet[Reference Rambo, Smith, Porter, Hurst, Speas, Adams, Garcia, Dawson, Thurston, Wakefield, Kellogg, Slattery, Ives, Broyles, Caird, Erlandson, Murray, Behrendt, Neilsen and Narduzzi17] laser was used to heat the gas, and set up a blast wave which pushes on the inside wall of the tube. A pair of Helmholtz coils[Reference Rovang, Lamppa, Cuneo, Owen, McKenney, Johnson, Radovich, Kaye, McBride, Alexander, Awe, Slutz, Sefkow, Haill, Jones, Argo, Dalton, Robertson, Waisman, Sinars, Meissner, Milhous, Nguyen and Mielke18] provided a uniform axial magnetic field of 9 T to the experiment. A VISAR diagnostic was placed on the outside of the aluminum tube at multiple axial and azimuthal locations, in order to measure the velocity outside surface of the tube. The tube itself represents the VISAR flyer in these experiments. Figure 4 shows a schematic of the MagLIF laser blast wave experiment.
$\text{D}_{\text{2}}$ gas fill at 57 psi. A 2 kJ laser pulse from the Sandia Z-Beamlet[Reference Rambo, Smith, Porter, Hurst, Speas, Adams, Garcia, Dawson, Thurston, Wakefield, Kellogg, Slattery, Ives, Broyles, Caird, Erlandson, Murray, Behrendt, Neilsen and Narduzzi17] laser was used to heat the gas, and set up a blast wave which pushes on the inside wall of the tube. A pair of Helmholtz coils[Reference Rovang, Lamppa, Cuneo, Owen, McKenney, Johnson, Radovich, Kaye, McBride, Alexander, Awe, Slutz, Sefkow, Haill, Jones, Argo, Dalton, Robertson, Waisman, Sinars, Meissner, Milhous, Nguyen and Mielke18] provided a uniform axial magnetic field of 9 T to the experiment. A VISAR diagnostic was placed on the outside of the aluminum tube at multiple axial and azimuthal locations, in order to measure the velocity outside surface of the tube. The tube itself represents the VISAR flyer in these experiments. Figure 4 shows a schematic of the MagLIF laser blast wave experiment.
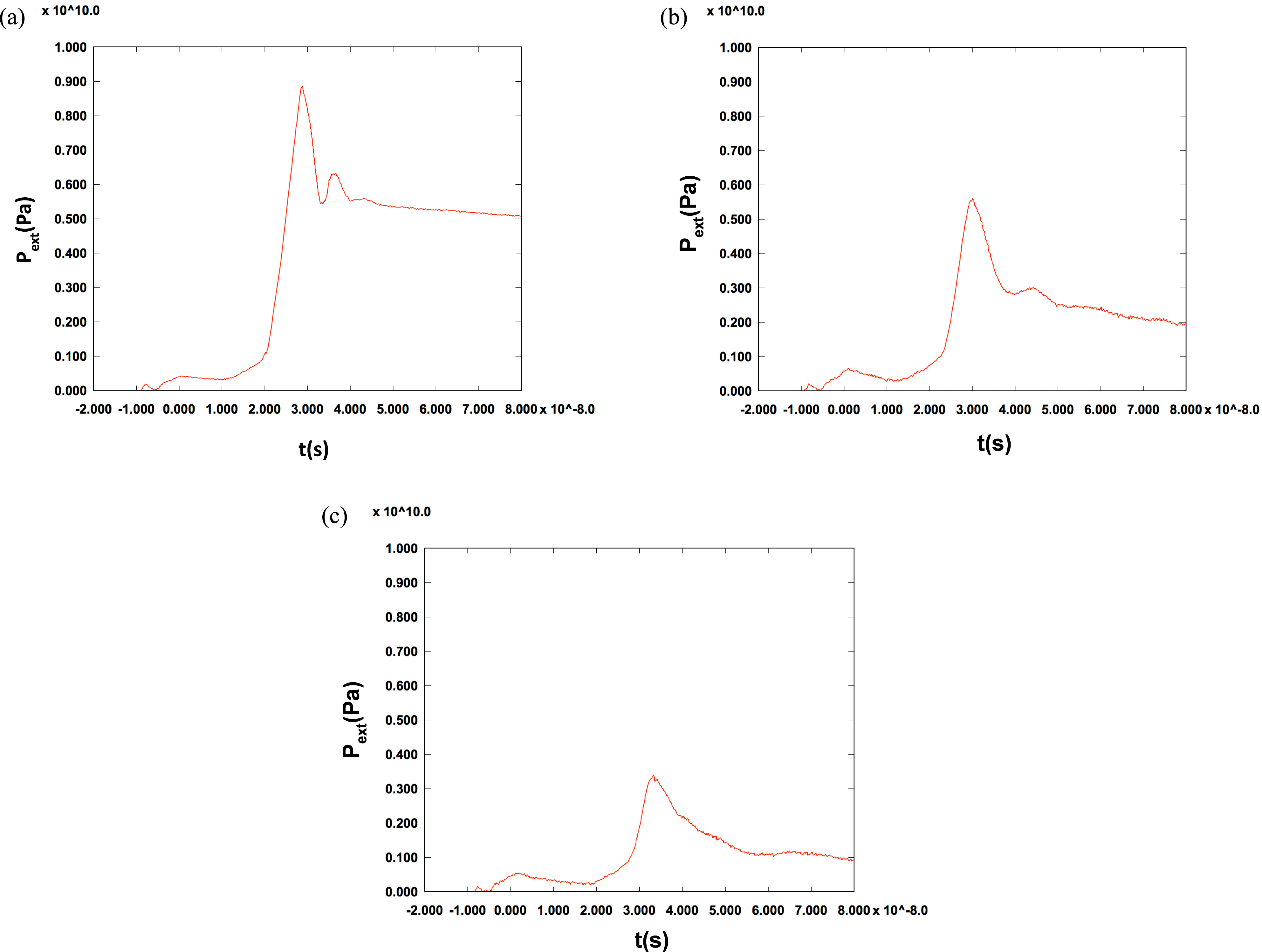
Figure 5. (a) Pressure unfold for laser blast wave experiment at 3.59 mm from LEH. (b) Pressure unfold for laser blast wave experiment at 5.71 mm from LEH. (c) Pressure unfold for laser blast wave experiment at 7.84 mm from LEH.
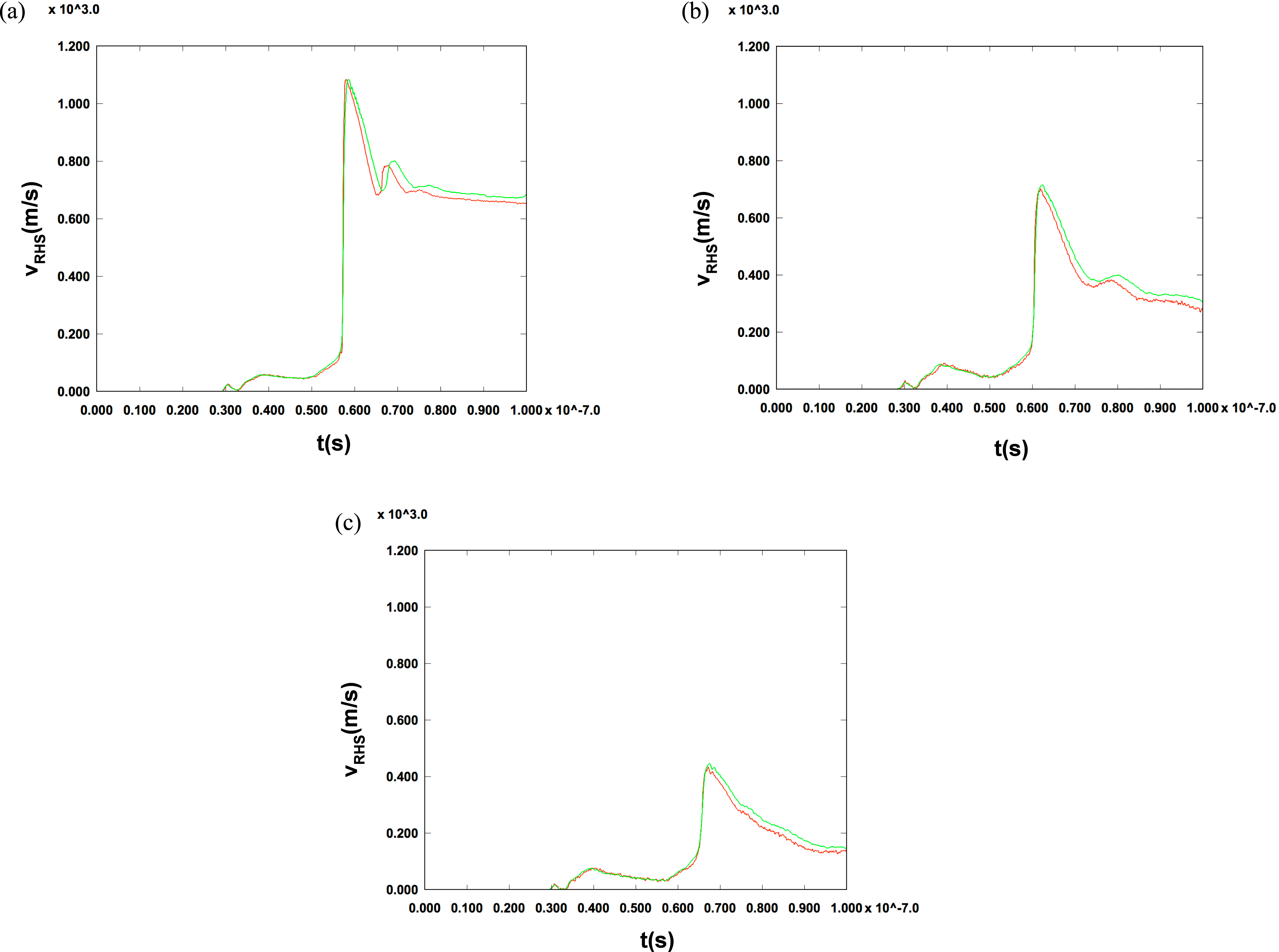
Figure 6. (a) Comparison of VISAR data (red) with velocity output from ALEGRA using the unfolded pressure (green) at 3.59 mm from LEH. (b) Comparison of VISAR data (red) with velocity output from ALEGRA using unfolded pressure (green) at 5.71 mm from LEH. (c) Comparison of VISAR data (red) with velocity output from ALEGRA using unfolded pressure (green) at 7.84 mm from LEH.
Figure 5(a–c) show the unfolded pressure using our unfold method and incorporating the Al3700 SESAME EOS table for the high-pressure section (![]() ${>}0.7~\text{GPa}$) at axial locations 3.59 mm, 5.71 mm and 7.84 mm below the laser entrance hole (LEH) respectively. For pressures below 0.7 GPa, the oscillator model in Equation (4) was utilized. The unfolded pressures are produced numerically using a Python script, which runs in less than 30 s. When implementing Equation (12) to convert all RHS VISAR data points into
${>}0.7~\text{GPa}$) at axial locations 3.59 mm, 5.71 mm and 7.84 mm below the laser entrance hole (LEH) respectively. For pressures below 0.7 GPa, the oscillator model in Equation (4) was utilized. The unfolded pressures are produced numerically using a Python script, which runs in less than 30 s. When implementing Equation (12) to convert all RHS VISAR data points into ![]() $P_{\text{ext}}(t)$ data points, we find that there is a subset of data points in which the time shift may be too great, giving rise to a
$P_{\text{ext}}(t)$ data points, we find that there is a subset of data points in which the time shift may be too great, giving rise to a ![]() $P_{\text{ext}}(t)$ which is multivalued in certain sections. As part of our method, we filter out data points later in the
$P_{\text{ext}}(t)$ which is multivalued in certain sections. As part of our method, we filter out data points later in the ![]() $P_{\text{ext}}(t)$ list that would give rise to a multivalued behavior. Typically, this behavior occurs near strong shocking events, such as near the pressure peak at 30 ns in Figure 5(a). Filtering the pressure data yields a single-valued pressure function that provides a velocity response in excellent agreement with the VISAR data, as we will now demonstrate.
$P_{\text{ext}}(t)$ list that would give rise to a multivalued behavior. Typically, this behavior occurs near strong shocking events, such as near the pressure peak at 30 ns in Figure 5(a). Filtering the pressure data yields a single-valued pressure function that provides a velocity response in excellent agreement with the VISAR data, as we will now demonstrate.
Using the unfolded pressure drives in Figure 5(a–c), we run ALEGRA simulations to produce RHS VISAR velocity outputs. Figure 6(a–c) show comparisons of the actual VISAR data with the ALEGRA simulation using the unfolded pressure drive. As one can see, the unfolded pressures produce RHS velocities that are in excellent agreement with the measured VISAR data. The low-pressure ‘foot’ of the pressure drive as well as the main pressure pulse give accurate comparisons to the VISAR data. However, there is a discrepancy, which occurs after the pressure peak. This is most likely due to effects at the RHS such as density reflections, which can vary nonlinearly the velocity and strength of incoming shocks, as well as the release wave, which can produce low-density regions in the flyer. Nevertheless, the unfold method that we just described provides a quick and accurate method for unfolding the pressure drive. Depending on the accuracy requirements of the unfold, this method may provide a final answer for the pressure history or could be used as a starting point for a more rigorous forward iterative unfold process using a HD simulation code, such as ALEGRA, in conjunction with an optimization code, such as DAKOTA[Reference Adams, Bohnhoff, Dalbey, Eddy, Eldred, Gay, Haskell, Hough and Swiler19]. A figure of merit, such as a least squares comparison of the simulated velocity and VISAR data, can be used to determine how to update the pressure drive with the optimization software.
Acknowledgements
M. Hess would like to thank K. Cochrane and T. Haill of Sandia National Laboratories for their helpful discussions. Sandia National Laboratories is a multiprogram laboratory managed and operated by Sandia Corporation, a wholly owned subsidiary of Lockheed Martin Corporation, for the U.S. Department of Energy’s National Nuclear Security Administration under Contract No. DE-AC04-94AL85000.








