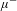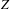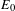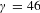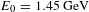1 Introduction
The muon[Reference Patrignani, Agashe, Aielli, Amsler, Antonelli, Asner, Baer, Banerjee, Barnett, Basaglia, Bauer, Beatty, Belousov, Beringer, Bethke, Bichsel, Biebel, Blucher, Brooijmans, Buchmueller, Burkert, Bychkov, Cahn, Carena, Ceccucci, Cerri, Chakraborty, Chen, Chivukula, Copic, Cowan, Dahl, D’Ambrosio, Damour, de Florian, de Gouvea, Degrand, de Jong, Dissertori, Dobrescu, Donofrio, Doser, Drees, Dreiner, Dwyer, Eerola, Eidelman, Ellis, Erler, Ezhela, Fetscher, Fields, Foster, Freitas, Gallagher, Garren, Gerber, Gerbier, Gershon, Gherghetta, Godizov, Goodman, Grab, Gritsan, Grojean, Groom, Grunewald, Gurtu, Gutsche, Haber, Hagiwara, Hanhart, Hashimoto, Hayato, Hayes, Hebecker, Heltsley, Hernández-Rey, Hikasa, Hisano, Höcker, Holder, Holtkamp, Huston, Hyodo, Irwin, Jackson, Johnson, Kado, Karliner, Katz, Klein, Klempt, Kowalewski, Krauss, Kreps, Krusche, Kuyanov, Kwon, Lahav, Laiho, Langacker, Liddle, Ligeti, Lin, Lippmann, Liss, Littenberg, Lugovsky, Lugovsky, Lusiani, Makida, Maltoni, Mannel, Manohar, Marciano, Martin, Masoni, Matthews, Meiner, Milstead, Mitchell, Molaro, Monig, Moortgat, Mortonson, Murayama, Nakamura, Narain, Nason, Navas, Neubert, Nevski, Nir, Olive, Pagan Griso, Parsons, Peacock, Pennington, Petcov, Petrov, Piepke, Pomarol, Quadt, Raby, Rademacker, Raffelt, Ratcliff, Richardson, Ringwald, Roesler, Rolli, Romaniouk, Rosenberg, Rosner, Rybka, Ryutin, Sachrajda, Sakai, Salam, Sarkar, Sauli, Schneider, Scholberg, Schwartz, Scott, Sharma, Sharpe, Shutt, Silari, Sjostrand, Skands, Skwarnicki, Smith, Smoot, Spanier, Spieler, Spiering, Stahl, Stone, Sumino, Sumiyoshi, Syphers, Takahashi, Tanabashi, Terashi, Terning, Thorne, Tiator, Titov, Tkachenko, Tornqvist, Tovey, Valencia, Van de Water, Varelas, Venanzoni, Vincter, Vogel, Vogt, Wakely, Walkowiak, Walter, Wands, Ward, Wascko, Weiglein, Weinberg, Weinberg, White, Wiencke, Willocq, Wohl, Wolfenstein, Womersley, Woody, Workman, Yao, Zeller, Zenin, Zhu, Zimmermann and Zyla1] plays a key role in particle physics and applied physics, such as the muon anomalous magnetic dipole moment
![]() $a\equiv (g-2)/2$
measurement[Reference Farley and Semertzidis2], muon collider and neutrino physics[Reference Palmer3], muon catalyzed fusion[Reference Ackerbauer, Werner, Breunlich, Cargnelli, Fussy, Jeitler, Kammel, Marton, Scrinzi, Zmeskal, Bistirlich, Crowe, Kurck, Petitjean, Sherman, Bossy, Daniel, Hartmann, Neumann, Schmidt and Faifman4], muon probe of the microscopic magnetic properties of materials[Reference Blundell5], and muon radiography[Reference Borozdin, Hogan, Morris, Priedhorsky, Saunders, Schultz and Teasdale6]. However, muon physics is limited by either the low flux cosmic-ray muons[Reference Nagamine7] or high cost accelerator muons[Reference Carne, Cox, Eaton and Scott8–Reference Marshall11].
$a\equiv (g-2)/2$
measurement[Reference Farley and Semertzidis2], muon collider and neutrino physics[Reference Palmer3], muon catalyzed fusion[Reference Ackerbauer, Werner, Breunlich, Cargnelli, Fussy, Jeitler, Kammel, Marton, Scrinzi, Zmeskal, Bistirlich, Crowe, Kurck, Petitjean, Sherman, Bossy, Daniel, Hartmann, Neumann, Schmidt and Faifman4], muon probe of the microscopic magnetic properties of materials[Reference Blundell5], and muon radiography[Reference Borozdin, Hogan, Morris, Priedhorsky, Saunders, Schultz and Teasdale6]. However, muon physics is limited by either the low flux cosmic-ray muons[Reference Nagamine7] or high cost accelerator muons[Reference Carne, Cox, Eaton and Scott8–Reference Marshall11].
Laser wakefield acceleration (LWFA), which promises the next generation compact high-energy electron beam source[Reference Esarey, Schroeder and Leemans12, Reference Lu, Huang, Zhou, Mori and Katsouleas13], could also have potential application in muon source researches. While electrons can be simply self-injected through wave-breaking, an external injection is needed for muons. Such external muons could be conveniently supplied by the Bethe–Heitler lepton pair production
![]() $\unicode[STIX]{x1D6FE}+A\rightarrow A^{^{\prime }}+\unicode[STIX]{x1D707}^{+}\unicode[STIX]{x1D707}^{-}$
proposed by Titov et al.
[Reference Titov, Kampfer and Takabe14], where the high-energy photons come from the LWFA electrons with energy up to several GeV[Reference Leemans, Nagler, Gonsalves, Toth, Nakamura, Geddes, Esarey, Schroeder and Hooker15–Reference Leemans, Gonsalves, Mao, Nakamura, Benedetti, Schroeder, Toth, Daniels, Mittelberger, Bulanov, Vay, Geddes and Esarey20] interacting with high
$\unicode[STIX]{x1D6FE}+A\rightarrow A^{^{\prime }}+\unicode[STIX]{x1D707}^{+}\unicode[STIX]{x1D707}^{-}$
proposed by Titov et al.
[Reference Titov, Kampfer and Takabe14], where the high-energy photons come from the LWFA electrons with energy up to several GeV[Reference Leemans, Nagler, Gonsalves, Toth, Nakamura, Geddes, Esarey, Schroeder and Hooker15–Reference Leemans, Gonsalves, Mao, Nakamura, Benedetti, Schroeder, Toth, Daniels, Mittelberger, Bulanov, Vay, Geddes and Esarey20] interacting with high
![]() $Z$
materials.
$Z$
materials.
![]() $10^{6}$
dimuons could be produced by a 100 J petawatt laser facility[Reference Titov, Kampfer and Takabe14] and diagnosed efficiently[Reference Zhang, Li, Shan, Zhang, Hong and Gu21]. But those muons with lower mean energies and broad energy spread ranging from hundreds of MeV to GeV[Reference Titov, Kampfer and Takabe14] limit the applications. On the other hand, those muons could be accelerated by the laser wakefield, called ‘bubble’, since the velocities are close or even higher than that of the bubble. Therefore for the first time we suggest an all-optical muon acceleration scheme as shown in Figure 1, in which muons could be generated by the Bethe–Heitler process via high-energy photons from the Bremsstrahlung radiation of the LWFA electrons interacting with the high
$10^{6}$
dimuons could be produced by a 100 J petawatt laser facility[Reference Titov, Kampfer and Takabe14] and diagnosed efficiently[Reference Zhang, Li, Shan, Zhang, Hong and Gu21]. But those muons with lower mean energies and broad energy spread ranging from hundreds of MeV to GeV[Reference Titov, Kampfer and Takabe14] limit the applications. On the other hand, those muons could be accelerated by the laser wakefield, called ‘bubble’, since the velocities are close or even higher than that of the bubble. Therefore for the first time we suggest an all-optical muon acceleration scheme as shown in Figure 1, in which muons could be generated by the Bethe–Heitler process via high-energy photons from the Bremsstrahlung radiation of the LWFA electrons interacting with the high
![]() $Z$
materials, called ‘Generator’, and boosted by another laser wakefield, called ‘Booster’.
$Z$
materials, called ‘Generator’, and boosted by another laser wakefield, called ‘Booster’.

Figure 1. All-optical ‘Generator and Booster’ scheme of muon source. Muons are first generated by the Bethe–Heitler process, the ‘Generator’, via high-energy photons from Bremsstrahlung radiation of laser wakefield accelerated electrons interacting with high
![]() $Z$
materials. After a proper collection and focusing system, muons are boosted by another laser wakefield, the ‘Booster’.
$Z$
materials. After a proper collection and focusing system, muons are boosted by another laser wakefield, the ‘Booster’.
This new all-optical ‘Generator and Booster’ scheme can supply a prompt, compact, low cost and controllable muon source which would have potential applications in muon collider, neutrino physics and Higgs Factory[Reference Palmer3], muon acceleration in cosmic-ray sources[Reference Klein, Mikkelsen and Tjus22] and other related muon physics. Peano et al. also proposed a scheme[Reference Peano, Vieira, Mulas, Coppa, Bingham and Silva23] to accelerate ‘cold’ muons by a slow ponderomotive beat-wave structure driven by two counterpropagating laser beams with variable frequencies which is quite different from the scheme proposed here.
In the scheme, the Generator would produce a muon bunch with short pulse duration, small source emittance and continuous energy distribution[Reference Titov, Kampfer and Takabe14]. In principle, muons produced in the Generator could be collected and focused to adapt the bubble’s size before injecting into the Booster by the plasma lens[Reference Steinke, van Tilborg, Benedetti, Geddes, Schroeder, Daniels, Swanson, Gonsalves, Nakamura, Matlis, Shaw, Esarey and Leemans24, Reference Kahn, Korenev, Bishai, Diwan, Gallardo, Hershcovitch and Johnson25] or magnetic quadrupoles lens[Reference Teng, Gu, Chen, Zhu, Zhang, Tan, Hong, Zhang and Wang26]. The time synchronization between Generator and Booster is also guaranteed in such an all-optical system. However, the huge invariant mass difference by a factor of 207 (
![]() $m_{\unicode[STIX]{x1D707}}=105.7~\text{MeV}/c^{2}$
) would result in different behaviors of muons compared to electron and positron accelerations in the bubble[Reference Leemans and Esarey27, Reference Song, Hu, Shou, Gong, Yu, Lin, Ma, Zhao, Lu and Yan28]. Therefore, considering the continuous energy[Reference Titov, Kampfer and Takabe14], the acceleration performance and phase matching of muons in the accelerated field of the bubble need to be studied in detail. It is worth to mention that the
$m_{\unicode[STIX]{x1D707}}=105.7~\text{MeV}/c^{2}$
) would result in different behaviors of muons compared to electron and positron accelerations in the bubble[Reference Leemans and Esarey27, Reference Song, Hu, Shou, Gong, Yu, Lin, Ma, Zhao, Lu and Yan28]. Therefore, considering the continuous energy[Reference Titov, Kampfer and Takabe14], the acceleration performance and phase matching of muons in the accelerated field of the bubble need to be studied in detail. It is worth to mention that the
![]() $\unicode[STIX]{x1D707}^{-}$
acceleration would be easier than that of
$\unicode[STIX]{x1D707}^{-}$
acceleration would be easier than that of
![]() $\unicode[STIX]{x1D707}^{+}$
in a nonlinear (bubble/blow-out) regime since the accelerating/focusing wakefields for
$\unicode[STIX]{x1D707}^{+}$
in a nonlinear (bubble/blow-out) regime since the accelerating/focusing wakefields for
![]() $\unicode[STIX]{x1D707}^{-}$
determined by background plasma density are much challenging for
$\unicode[STIX]{x1D707}^{-}$
determined by background plasma density are much challenging for
![]() $\unicode[STIX]{x1D707}^{+}$
same as in the cases of positrons[Reference Rosenzweig, Cook, Scott, Tompson and Yoder29]. In this paper, we focus on the
$\unicode[STIX]{x1D707}^{+}$
same as in the cases of positrons[Reference Rosenzweig, Cook, Scott, Tompson and Yoder29]. In this paper, we focus on the
![]() $\unicode[STIX]{x1D707}^{-}$
acceleration. Hereafter in this paper muon denotes
$\unicode[STIX]{x1D707}^{-}$
acceleration. Hereafter in this paper muon denotes
![]() $\unicode[STIX]{x1D707}^{-}$
.
$\unicode[STIX]{x1D707}^{-}$
.
In this paper, we investigate the trapping and acceleration of muons with continuous energy distribution from the ‘Generator’. The motion of muons is analyzed by one-dimensional analytic model and verified by two-dimensional particle-in-cell (PIC) simulation of a typical laser wakefield. It is shown that muons can be trapped in a broad energy range and accelerated to higher energy than that of electrons for longer dephasing length. We further extrapolate the muon acceleration to anticipate a muon energy up to 15.2 GeV on the existent short pulse laser facilities, which is exciting for the application in the laser laboratories.

Figure 2. (a) The bubble’s electron density and (b) electrostatic field in the simulation box were obtained from a two-dimensional particle-in-cell simulation code Opic2D for a plasma density
![]() $2\times 10^{-3}n_{c}$
. The laser pulse of wavelength
$2\times 10^{-3}n_{c}$
. The laser pulse of wavelength
![]() $0.8~\unicode[STIX]{x03BC}\text{m}$
, normalized peak amplitude
$0.8~\unicode[STIX]{x03BC}\text{m}$
, normalized peak amplitude
![]() $a_{0}=2$
, pulse duration 33 fs and FWHM spot size
$a_{0}=2$
, pulse duration 33 fs and FWHM spot size
![]() $18~\unicode[STIX]{x03BC}\text{m}$
entered from the left of the simulation box in the
$18~\unicode[STIX]{x03BC}\text{m}$
entered from the left of the simulation box in the
![]() $x$
direction. A muon with critical trapping energy entered into the simulation box following the trajectory shown in (c) and the energy increasing process in (d).
$x$
direction. A muon with critical trapping energy entered into the simulation box following the trajectory shown in (c) and the energy increasing process in (d).
2 Muon motion in one-dimensional analytic model
We first illustrate a typical laser wakefield in Figure 2(a) using the two-dimensional PIC simulation code Opic2D. A linearly polarized pulse of wavelength
![]() $\unicode[STIX]{x1D706}_{0}=0.8~\unicode[STIX]{x03BC}\text{m}$
, normalized peak amplitude
$\unicode[STIX]{x1D706}_{0}=0.8~\unicode[STIX]{x03BC}\text{m}$
, normalized peak amplitude
![]() $a_{0}=2$
, pulse duration 33 fs and full width at half-maximum (FWHM) spot size
$a_{0}=2$
, pulse duration 33 fs and full width at half-maximum (FWHM) spot size
![]() $18~\unicode[STIX]{x03BC}\text{m}$
enters from the left of the simulation box of size
$18~\unicode[STIX]{x03BC}\text{m}$
enters from the left of the simulation box of size
![]() $100\unicode[STIX]{x1D706}_{0}\times 60\unicode[STIX]{x1D706}_{0}$
. A plasma of electron density
$100\unicode[STIX]{x1D706}_{0}\times 60\unicode[STIX]{x1D706}_{0}$
. A plasma of electron density
![]() $2.2\times 10^{18}\unicode[STIX]{x1D706}_{0}^{-2}~\text{cm}^{-3}$
(0.002
$2.2\times 10^{18}\unicode[STIX]{x1D706}_{0}^{-2}~\text{cm}^{-3}$
(0.002
![]() $n_{c}$
) is located in
$n_{c}$
) is located in
![]() $40\unicode[STIX]{x1D706}_{0}<x<100\unicode[STIX]{x1D706}_{0}$
. There are 4000
$40\unicode[STIX]{x1D706}_{0}<x<100\unicode[STIX]{x1D706}_{0}$
. There are 4000
![]() $\times$
600 cells in the simulation windows. The particle number per cell is 4 for both electron and muon. Open boundaries are applied in both longitudinal and transverse directions. A moving window is applied in the simulation with velocity
$\times$
600 cells in the simulation windows. The particle number per cell is 4 for both electron and muon. Open boundaries are applied in both longitudinal and transverse directions. A moving window is applied in the simulation with velocity
![]() $v_{p}$
which is consistent with the laser group velocity (normalized by the light speed
$v_{p}$
which is consistent with the laser group velocity (normalized by the light speed
![]() $c$
) reading from the simulation. The lineout on-axis electrostatic field in the moving window (i.e., in the rest frame of the bubble) is shown in Figure 2(b).
$c$
) reading from the simulation. The lineout on-axis electrostatic field in the moving window (i.e., in the rest frame of the bubble) is shown in Figure 2(b).
We analyze the motion of muons in such a laser wakefield in a one-dimensional analytic model. Similar as electrons, only muons locate in
![]() $\unicode[STIX]{x1D709}_{L}<\unicode[STIX]{x1D709}<\unicode[STIX]{x1D709}_{R}$
in the electrostatic field shown in Figure 2(b) are accelerated. The two zero points of
$\unicode[STIX]{x1D709}_{L}<\unicode[STIX]{x1D709}<\unicode[STIX]{x1D709}_{R}$
in the electrostatic field shown in Figure 2(b) are accelerated. The two zero points of
![]() $E(\unicode[STIX]{x1D709})$
are defined as
$E(\unicode[STIX]{x1D709})$
are defined as
![]() $\unicode[STIX]{x1D709}_{L}=0~\unicode[STIX]{x03BC}\text{m}$
and
$\unicode[STIX]{x1D709}_{L}=0~\unicode[STIX]{x03BC}\text{m}$
and
![]() $\unicode[STIX]{x1D709}_{R}=13~\unicode[STIX]{x03BC}\text{m}$
with
$\unicode[STIX]{x1D709}_{R}=13~\unicode[STIX]{x03BC}\text{m}$
with
![]() $\unicode[STIX]{x1D709}$
denoting the position in the rest frame of the bubble. Considering the initial energy of muons
$\unicode[STIX]{x1D709}$
denoting the position in the rest frame of the bubble. Considering the initial energy of muons
![]() $E_{0}$
and position
$E_{0}$
and position
![]() $\unicode[STIX]{x1D709}_{0}$
, the position of the muon in the rest frame of the bubble is
$\unicode[STIX]{x1D709}_{0}$
, the position of the muon in the rest frame of the bubble is
where the muon velocity
![]() $v_{\unicode[STIX]{x1D707}}=v_{\unicode[STIX]{x1D707}}(t)$
can be written as
$v_{\unicode[STIX]{x1D707}}=v_{\unicode[STIX]{x1D707}}(t)$
can be written as
where
![]() $\unicode[STIX]{x1D6FE}_{0}=E_{0}/m_{\unicode[STIX]{x1D707}}+1$
is the relativistic factor with the muon mass
$\unicode[STIX]{x1D6FE}_{0}=E_{0}/m_{\unicode[STIX]{x1D707}}+1$
is the relativistic factor with the muon mass
![]() $m_{\unicode[STIX]{x1D707}}=105.7~\text{MeV}/c^{2}$
, charge
$m_{\unicode[STIX]{x1D707}}=105.7~\text{MeV}/c^{2}$
, charge
![]() $q=-1$
, and
$q=-1$
, and
![]() $E(\unicode[STIX]{x1D709})$
reads from Figure 2(b). Because the muon is heavier than the electron by a factor of 207, the velocity of accelerated muons is lower than that of electrons which is generally taken as the light speed
$E(\unicode[STIX]{x1D709})$
reads from Figure 2(b). Because the muon is heavier than the electron by a factor of 207, the velocity of accelerated muons is lower than that of electrons which is generally taken as the light speed
![]() $c$
.
$c$
.
For convenience, we define forward phase (
![]() $v_{\unicode[STIX]{x1D707}}>v_{p}$
) and backward phase (
$v_{\unicode[STIX]{x1D707}}>v_{p}$
) and backward phase (
![]() $v_{\unicode[STIX]{x1D707}}<v_{p}$
) denoting the initial direction of the muon in the rest frame of the bubble as shown in Figure 2(c). Giving finite laser and plasma condition, the trapping condition of muons is
$v_{\unicode[STIX]{x1D707}}<v_{p}$
) denoting the initial direction of the muon in the rest frame of the bubble as shown in Figure 2(c). Giving finite laser and plasma condition, the trapping condition of muons is
![]() $v_{\unicode[STIX]{x1D707}}=v_{p}$
at
$v_{\unicode[STIX]{x1D707}}=v_{p}$
at
![]() $\unicode[STIX]{x1D709}=\unicode[STIX]{x1D709}_{L}$
. Therefore, backward muons should be located at
$\unicode[STIX]{x1D709}=\unicode[STIX]{x1D709}_{L}$
. Therefore, backward muons should be located at
![]() $\unicode[STIX]{x1D709}=\unicode[STIX]{x1D709}_{R}$
to achieve sufficient acceleration. As an example, a backward muon with critical trapping energy located at
$\unicode[STIX]{x1D709}=\unicode[STIX]{x1D709}_{R}$
to achieve sufficient acceleration. As an example, a backward muon with critical trapping energy located at
![]() $\unicode[STIX]{x1D709}_{0}=\unicode[STIX]{x1D709}_{R}$
would fall back to
$\unicode[STIX]{x1D709}_{0}=\unicode[STIX]{x1D709}_{R}$
would fall back to
![]() $\unicode[STIX]{x1D709}=\unicode[STIX]{x1D709}_{L}$
in the rest frame of the bubble with velocity climbing up to
$\unicode[STIX]{x1D709}=\unicode[STIX]{x1D709}_{L}$
in the rest frame of the bubble with velocity climbing up to
![]() $v_{p}$
. After that the muon turns into forward phase until flying over the bubble region. The whole process would follow the trajectory shown in Figure 2(c) and the energy increasing in Figure 2(d).
$v_{p}$
. After that the muon turns into forward phase until flying over the bubble region. The whole process would follow the trajectory shown in Figure 2(c) and the energy increasing in Figure 2(d).

Figure 3. (a) The estimated acceleration energy of muons
![]() $E_{\text{acc}}$
depending on the initial energy
$E_{\text{acc}}$
depending on the initial energy
![]() $E_{0}$
with different positions in the rest frame of bubble
$E_{0}$
with different positions in the rest frame of bubble
![]() $\unicode[STIX]{x1D709}_{0}\in [0,1,3,5,7,9,13]~\unicode[STIX]{x03BC}\text{m}$
from the one-dimensional analytical model denoted by the solid lines. Clearly trapping energy thresholds presented from the sharp peaks of the lines. The two-dimensional PIC simulations of the forward (red dots) and backward (blue dots) muons at
$\unicode[STIX]{x1D709}_{0}\in [0,1,3,5,7,9,13]~\unicode[STIX]{x03BC}\text{m}$
from the one-dimensional analytical model denoted by the solid lines. Clearly trapping energy thresholds presented from the sharp peaks of the lines. The two-dimensional PIC simulations of the forward (red dots) and backward (blue dots) muons at
![]() $t=33~\text{ps}$
show well agreement with the one-dimensional estimation. (b) The inner plot shows the spectra of the forward (red lines) and backward (blue lines) muons, where dashed lines denote the initialized energy spectra and the solid lines denote the acceleration energy spectra at
$t=33~\text{ps}$
show well agreement with the one-dimensional estimation. (b) The inner plot shows the spectra of the forward (red lines) and backward (blue lines) muons, where dashed lines denote the initialized energy spectra and the solid lines denote the acceleration energy spectra at
![]() $t=33~\text{ps}$
.
$t=33~\text{ps}$
.

Figure 4. The snapshots of the acceleration processes of forward (red dots) and backward (blue dots) muons from the two-dimensional PIC simulations in Figure 2 at (a)
![]() $t=0.33$
ps, (b) 1.65 ps, (c) 16.5 ps and (d) 33 ps. (e)–(h) The
$t=0.33$
ps, (b) 1.65 ps, (c) 16.5 ps and (d) 33 ps. (e)–(h) The
![]() $x\text{-}p_{x}$
and (i)–(l)
$x\text{-}p_{x}$
and (i)–(l)
![]() $y\text{-}p_{y}$
phase spaces of forward (red dots) and backward (blue dots) muons at the four snapshots are also shown, respectively.
$y\text{-}p_{y}$
phase spaces of forward (red dots) and backward (blue dots) muons at the four snapshots are also shown, respectively.
Then the trajectories of muons giving
![]() $E_{0}$
and
$E_{0}$
and
![]() $\unicode[STIX]{x1D709}_{0}$
can be calculated with this analytic model. Giving
$\unicode[STIX]{x1D709}_{0}$
can be calculated with this analytic model. Giving
![]() $\unicode[STIX]{x1D709}_{L}<\unicode[STIX]{x1D709}_{0}<\unicode[STIX]{x1D709}_{R}$
, we choose the
$\unicode[STIX]{x1D709}_{L}<\unicode[STIX]{x1D709}_{0}<\unicode[STIX]{x1D709}_{R}$
, we choose the
![]() $E_{0}$
randomly from 0.2 GeV to 2.0 GeV. When muons drop into
$E_{0}$
randomly from 0.2 GeV to 2.0 GeV. When muons drop into
![]() $\unicode[STIX]{x1D709}<\unicode[STIX]{x1D709}_{L}$
or
$\unicode[STIX]{x1D709}<\unicode[STIX]{x1D709}_{L}$
or
![]() $\unicode[STIX]{x1D709}>\unicode[STIX]{x1D709}_{R}$
regions, the final acceleration energy is recorded as
$\unicode[STIX]{x1D709}>\unicode[STIX]{x1D709}_{R}$
regions, the final acceleration energy is recorded as
![]() $E_{\text{acc}}$
. We calculate the trajectories for
$E_{\text{acc}}$
. We calculate the trajectories for
![]() $\unicode[STIX]{x1D709}_{0}\in [0,1,3,5,7,9,13]~\unicode[STIX]{x03BC}\text{m}$
which are solid lines in Figure 3(a). Clearly energy thresholds for trapping
$\unicode[STIX]{x1D709}_{0}\in [0,1,3,5,7,9,13]~\unicode[STIX]{x03BC}\text{m}$
which are solid lines in Figure 3(a). Clearly energy thresholds for trapping
![]() $E_{c}(\unicode[STIX]{x1D709}_{0})$
are presented by the sharp peaks of the lines. Muons located at
$E_{c}(\unicode[STIX]{x1D709}_{0})$
are presented by the sharp peaks of the lines. Muons located at
![]() $\unicode[STIX]{x1D709}_{L}=0~\unicode[STIX]{x03BC}\text{m}$
have the highest trapping energy threshold
$\unicode[STIX]{x1D709}_{L}=0~\unicode[STIX]{x03BC}\text{m}$
have the highest trapping energy threshold
![]() $E_{c}(\unicode[STIX]{x1D709}_{L})=1.06~\text{GeV}$
and
$E_{c}(\unicode[STIX]{x1D709}_{L})=1.06~\text{GeV}$
and
![]() $\unicode[STIX]{x1D709}_{R}=13~\unicode[STIX]{x03BC}\text{m}$
the lowest
$\unicode[STIX]{x1D709}_{R}=13~\unicode[STIX]{x03BC}\text{m}$
the lowest
![]() $E_{c}(\unicode[STIX]{x1D709}_{R})=0.55~\text{GeV}$
. Here we take
$E_{c}(\unicode[STIX]{x1D709}_{R})=0.55~\text{GeV}$
. Here we take
![]() $\unicode[STIX]{x1D709}_{0}=\unicode[STIX]{x1D709}_{R}$
and
$\unicode[STIX]{x1D709}_{0}=\unicode[STIX]{x1D709}_{R}$
and
![]() $\unicode[STIX]{x1D709}_{0}=\unicode[STIX]{x1D709}_{L}$
cases to discuss the acceleration pictures of muons in such an electrostatic field.
$\unicode[STIX]{x1D709}_{0}=\unicode[STIX]{x1D709}_{L}$
cases to discuss the acceleration pictures of muons in such an electrostatic field.
For
![]() $\unicode[STIX]{x1D709}_{0}=\unicode[STIX]{x1D709}_{R}$
case,
$\unicode[STIX]{x1D709}_{0}=\unicode[STIX]{x1D709}_{R}$
case,
![]() $E_{0}<E_{c}(\unicode[STIX]{x1D709}_{R})$
muons would drop out of the bubble as
$E_{0}<E_{c}(\unicode[STIX]{x1D709}_{R})$
muons would drop out of the bubble as
![]() $v_{\unicode[STIX]{x1D707}}<v_{p}$
when falling back to
$v_{\unicode[STIX]{x1D707}}<v_{p}$
when falling back to
![]() $\unicode[STIX]{x1D709}=\unicode[STIX]{x1D709}_{L}$
and
$\unicode[STIX]{x1D709}=\unicode[STIX]{x1D709}_{L}$
and
![]() $E_{0}>E_{c}(\unicode[STIX]{x1D709}_{R})$
muons change to forward phase before falling back to
$E_{0}>E_{c}(\unicode[STIX]{x1D709}_{R})$
muons change to forward phase before falling back to
![]() $\unicode[STIX]{x1D709}=\unicode[STIX]{x1D709}_{L}$
resulting in insufficient acceleration, which illustrate the decline from the maximum acceleration energy. For higher
$\unicode[STIX]{x1D709}=\unicode[STIX]{x1D709}_{L}$
resulting in insufficient acceleration, which illustrate the decline from the maximum acceleration energy. For higher
![]() $E_{0}>E_{c}(\unicode[STIX]{x1D709}_{L})$
, muons dephase directly. Thus the lowest boundary of the solid line in Figure 3(a) corresponds to
$E_{0}>E_{c}(\unicode[STIX]{x1D709}_{L})$
, muons dephase directly. Thus the lowest boundary of the solid line in Figure 3(a) corresponds to
![]() $E_{\text{acc}}=E_{0}$
.
$E_{\text{acc}}=E_{0}$
.
For
![]() $\unicode[STIX]{x1D709}=\unicode[STIX]{x1D709}_{L}$
case,
$\unicode[STIX]{x1D709}=\unicode[STIX]{x1D709}_{L}$
case,
![]() $E_{0}<E_{c}(\unicode[STIX]{x1D709}_{L})$
muons drop out of the bubble without trapping. It is worth to mention that muons with higher energy (
$E_{0}<E_{c}(\unicode[STIX]{x1D709}_{L})$
muons drop out of the bubble without trapping. It is worth to mention that muons with higher energy (
![]() $E_{0}>E_{c}(\unicode[STIX]{x1D709}_{L})$
) would dephase more quickly resulting in less energy gain than the
$E_{0}>E_{c}(\unicode[STIX]{x1D709}_{L})$
) would dephase more quickly resulting in less energy gain than the
![]() $E_{0}=E_{c}(\unicode[STIX]{x1D709}_{L})$
case. As a result, the energy spread of muons would be narrowed.
$E_{0}=E_{c}(\unicode[STIX]{x1D709}_{L})$
case. As a result, the energy spread of muons would be narrowed.
For
![]() $\unicode[STIX]{x1D709}_{L}<\unicode[STIX]{x1D709}<\unicode[STIX]{x1D709}_{R}$
case, lines stand above the
$\unicode[STIX]{x1D709}_{L}<\unicode[STIX]{x1D709}<\unicode[STIX]{x1D709}_{R}$
case, lines stand above the
![]() $E_{\text{acc}}=E_{0}$
boundary (the lowest boundary in Figure 3(a)) which means in a broad energy range
$E_{\text{acc}}=E_{0}$
boundary (the lowest boundary in Figure 3(a)) which means in a broad energy range
![]() $E_{0}>E_{c}(\unicode[STIX]{x1D709})$
muons could be accelerated efficiently as our expectation. The reason is even with such a broad energy spread, the velocity of muons can still follow a narrow velocity distribution adapting to the bubble’s velocity.
$E_{0}>E_{c}(\unicode[STIX]{x1D709})$
muons could be accelerated efficiently as our expectation. The reason is even with such a broad energy spread, the velocity of muons can still follow a narrow velocity distribution adapting to the bubble’s velocity.
3 Muon motion in the two-dimensional PIC simulation
With the estimation of the one-dimensional analytic model, we choose a flat energy distribution range from 0.7 GeV to 2.2 GeV with initial position
![]() $\unicode[STIX]{x1D709}\in [0,1]~\unicode[STIX]{x03BC}\text{m}$
denoting the forward muons and energy range from 0.2 GeV to 1.2 GeV with initial position
$\unicode[STIX]{x1D709}\in [0,1]~\unicode[STIX]{x03BC}\text{m}$
denoting the forward muons and energy range from 0.2 GeV to 1.2 GeV with initial position
![]() $\unicode[STIX]{x1D709}\in [10,13]~\unicode[STIX]{x03BC}\text{m}$
denoting the backward muons in the two-dimensional PIC simulation. The muons are located in
$\unicode[STIX]{x1D709}\in [10,13]~\unicode[STIX]{x03BC}\text{m}$
denoting the backward muons in the two-dimensional PIC simulation. The muons are located in
![]() $18~\unicode[STIX]{x03BC}\text{m}<y<42~\unicode[STIX]{x03BC}\text{m}$
in the transverse direction with a density of
$18~\unicode[STIX]{x03BC}\text{m}<y<42~\unicode[STIX]{x03BC}\text{m}$
in the transverse direction with a density of
![]() $2\times 10^{-8}n_{c}$
(roughly
$2\times 10^{-8}n_{c}$
(roughly
![]() $5\times 10^{4}$
muons located in a
$5\times 10^{4}$
muons located in a
![]() $\unicode[STIX]{x1D70B}~\unicode[STIX]{x03BC}\text{m}\times 12^{2}~\unicode[STIX]{x03BC}\text{m}\times 3~\unicode[STIX]{x03BC}\text{m}$
plate), which is lower enough to avoid disturbing the bubble’s plasma structure. In the simulation, we trigger the movement of muons in
$\unicode[STIX]{x1D70B}~\unicode[STIX]{x03BC}\text{m}\times 12^{2}~\unicode[STIX]{x03BC}\text{m}\times 3~\unicode[STIX]{x03BC}\text{m}$
plate), which is lower enough to avoid disturbing the bubble’s plasma structure. In the simulation, we trigger the movement of muons in
![]() $x$
direction when the bubble structure is formed. The snapshots in Figure 4 show the acceleration processes of these two groups of muons at
$x$
direction when the bubble structure is formed. The snapshots in Figure 4 show the acceleration processes of these two groups of muons at
![]() $t=0.33~\text{ps}$
, 1.65 ps, 16.5 ps and 33 ps, respectively.
$t=0.33~\text{ps}$
, 1.65 ps, 16.5 ps and 33 ps, respectively.
We see in Figure 4(a), at
![]() $t=0.33~\text{ps}$
, that a typical electron bubble structure is formed. The forward muons (red dots) and backward muons (blue dots) are located around the initial positions. At
$t=0.33~\text{ps}$
, that a typical electron bubble structure is formed. The forward muons (red dots) and backward muons (blue dots) are located around the initial positions. At
![]() $t=1.65~\text{ps}$
in Figure 4(b), the backward muons are focused by the transversal field
$t=1.65~\text{ps}$
in Figure 4(b), the backward muons are focused by the transversal field
![]() $E_{y}$
. Part of the forward and backward muons with lower energy have dropped out of the bubble from the left side (
$E_{y}$
. Part of the forward and backward muons with lower energy have dropped out of the bubble from the left side (
![]() $\unicode[STIX]{x1D709}<0$
). At
$\unicode[STIX]{x1D709}<0$
). At
![]() $t=16.5~\text{ps}$
in Figure 4(c), both forward and backward muons are accelerated in the bubble sufficiently. However, the bubble structure has become unstable for the perturbation of laser transmission in the plasma. Finally at
$t=16.5~\text{ps}$
in Figure 4(c), both forward and backward muons are accelerated in the bubble sufficiently. However, the bubble structure has become unstable for the perturbation of laser transmission in the plasma. Finally at
![]() $t=33~\text{ps}$
in Figure 4(d), the bubble structure is almost absent. Both of the forward and backward muons fly freely. The
$t=33~\text{ps}$
in Figure 4(d), the bubble structure is almost absent. Both of the forward and backward muons fly freely. The
![]() $x\text{-}p_{x}$
and
$x\text{-}p_{x}$
and
![]() $y\text{-}p_{y}$
phase spaces of forward (red dots) and backward (blue dots) muons at the four snapshots are also shown, respectively, in Figure 4(e)–4(l). The oscillations of the two groups of muons in the
$y\text{-}p_{y}$
phase spaces of forward (red dots) and backward (blue dots) muons at the four snapshots are also shown, respectively, in Figure 4(e)–4(l). The oscillations of the two groups of muons in the
![]() $y\text{-}p_{y}$
phase space present effective constraints by the transversal field
$y\text{-}p_{y}$
phase space present effective constraints by the transversal field
![]() $E_{y}$
which would result in fine beam collimation.
$E_{y}$
which would result in fine beam collimation.
The
![]() $E_{0}$
and
$E_{0}$
and
![]() $E_{\text{acc}}$
of muons at
$E_{\text{acc}}$
of muons at
![]() $t=33~\text{ps}$
are plotted in Figure 3(a). Clearly consistency and same trends exhibit as the expectation from the one-dimensional analytic model especially the sharp peaks of the lines denoting the trapping energy thresholds for different initial positions. The trapping energy thresholds are higher than the one-dimensional model estimations because the bubble structure distortion is not considered in the analytic model. Furthermore, in Figure 3(b), the energy spectra of both groups of muons are narrowed after the acceleration as expected.
$t=33~\text{ps}$
are plotted in Figure 3(a). Clearly consistency and same trends exhibit as the expectation from the one-dimensional analytic model especially the sharp peaks of the lines denoting the trapping energy thresholds for different initial positions. The trapping energy thresholds are higher than the one-dimensional model estimations because the bubble structure distortion is not considered in the analytic model. Furthermore, in Figure 3(b), the energy spectra of both groups of muons are narrowed after the acceleration as expected.

Figure 5. The extrapolated relationships of the maximum acceleration energy of muons depending on (a) the bubble’s relativistic factor
![]() $\unicode[STIX]{x1D6FE}$
and (b) the relevant trapping energy threshold
$\unicode[STIX]{x1D6FE}$
and (b) the relevant trapping energy threshold
![]() $E_{0}$
from the one-dimensional analytic model. The extrapolation of electrons (open circles) in the same parameters is also shown for comparison.
$E_{0}$
from the one-dimensional analytic model. The extrapolation of electrons (open circles) in the same parameters is also shown for comparison.
4 Extrapolation of muon acceleration in laser wakefield
The good agreement of the one- and two-dimensional simulations gives us more confidence to extrapolate the estimation of muon acceleration. Obviously, to accelerate muons to higher energies, longer dephasing time is needed. Therefore the relativistic factor of the bubble
![]() $\unicode[STIX]{x1D6FE}$
would be the most important parameter in the extrapolation. The initial energy of muons
$\unicode[STIX]{x1D6FE}$
would be the most important parameter in the extrapolation. The initial energy of muons
![]() $E_{0}$
is another important parameter for the finite muon energy from the ‘Generator’. Considering the status of LWFA electrons up to now[Reference Leemans, Nagler, Gonsalves, Toth, Nakamura, Geddes, Esarey, Schroeder and Hooker15–Reference Leemans, Gonsalves, Mao, Nakamura, Benedetti, Schroeder, Toth, Daniels, Mittelberger, Bulanov, Vay, Geddes and Esarey20], we set the maximum
$E_{0}$
is another important parameter for the finite muon energy from the ‘Generator’. Considering the status of LWFA electrons up to now[Reference Leemans, Nagler, Gonsalves, Toth, Nakamura, Geddes, Esarey, Schroeder and Hooker15–Reference Leemans, Gonsalves, Mao, Nakamura, Benedetti, Schroeder, Toth, Daniels, Mittelberger, Bulanov, Vay, Geddes and Esarey20], we set the maximum
![]() $E_{0}=1.5~\text{GeV}$
. With the one-dimensional analytic model, we estimate the extrapolated relationships of the maximum acceleration energies of muons
$E_{0}=1.5~\text{GeV}$
. With the one-dimensional analytic model, we estimate the extrapolated relationships of the maximum acceleration energies of muons
![]() $E_{\text{acc}}$
depending on the bubble’s relativistic factor
$E_{\text{acc}}$
depending on the bubble’s relativistic factor
![]() $\unicode[STIX]{x1D6FE}\in [10,45]$
in Figure 5(a). For each setting of the bubble’s relativistic factor
$\unicode[STIX]{x1D6FE}\in [10,45]$
in Figure 5(a). For each setting of the bubble’s relativistic factor
![]() $\unicode[STIX]{x1D6FE}$
, the relevant trapping energy threshold
$\unicode[STIX]{x1D6FE}$
, the relevant trapping energy threshold
![]() $E_{0}$
is different which is shown in Figure 5(b). We can see that giving the relativistic factor of the bubble
$E_{0}$
is different which is shown in Figure 5(b). We can see that giving the relativistic factor of the bubble
![]() $\unicode[STIX]{x1D6FE}=46$
and the initial energy
$\unicode[STIX]{x1D6FE}=46$
and the initial energy
![]() $E_{0}=1.45~\text{GeV}$
, the extrapolated maximum acceleration energy of muons could be up to 15.2 GeV. To obtain such high-energy muons, one needs to accelerate muons for 300 ps in the bubble’s plasma channel (plasma density is
$E_{0}=1.45~\text{GeV}$
, the extrapolated maximum acceleration energy of muons could be up to 15.2 GeV. To obtain such high-energy muons, one needs to accelerate muons for 300 ps in the bubble’s plasma channel (plasma density is
![]() $0.00045n_{c}$
and length 9 cm) which has been realized in the experiment[Reference Leemans, Gonsalves, Mao, Nakamura, Benedetti, Schroeder, Toth, Daniels, Mittelberger, Bulanov, Vay, Geddes and Esarey20]. To accelerate muons to more higher energy such as a Higgs factory, a collision energy of around 125 GeV (muon energy 62.5 GeV) is needed which requires lower plasma density (plasma density is
$0.00045n_{c}$
and length 9 cm) which has been realized in the experiment[Reference Leemans, Gonsalves, Mao, Nakamura, Benedetti, Schroeder, Toth, Daniels, Mittelberger, Bulanov, Vay, Geddes and Esarey20]. To accelerate muons to more higher energy such as a Higgs factory, a collision energy of around 125 GeV (muon energy 62.5 GeV) is needed which requires lower plasma density (plasma density is
![]() $0.00008n_{c}$
and length 46 cm) and higher relativistic factor (
$0.00008n_{c}$
and length 46 cm) and higher relativistic factor (
![]() $\unicode[STIX]{x1D6FE}\approx 110$
) than the plasma channel in the literature. This kind of plasma channel has not been actualized but it might be realized in the future.
$\unicode[STIX]{x1D6FE}\approx 110$
) than the plasma channel in the literature. This kind of plasma channel has not been actualized but it might be realized in the future.
We have also shown the extrapolation of electron acceleration in the same parameters for comparison as the dashed line in Figure 5(a), in which we can find that the maximum acceleration of muons is larger than that of electrons by a factor of 2 to 3 for longer dephasing length. In fact, the dephasing length of trapped electrons reads[Reference Lu, Tzoufras, Joshi, Tsung, Mori, Vieira, Fonseca and Silva30]
where
![]() $\unicode[STIX]{x1D708}_{e}$
denotes the electron velocity,
$\unicode[STIX]{x1D708}_{e}$
denotes the electron velocity,
![]() $R=\unicode[STIX]{x1D709}_{R}-\unicode[STIX]{x1D709}_{L}$
denotes the acceleration interval and
$R=\unicode[STIX]{x1D709}_{R}-\unicode[STIX]{x1D709}_{L}$
denotes the acceleration interval and
![]() $\unicode[STIX]{x1D708}_{p}$
denotes the phase velocity of the bubble. Considering similar energy gain around GeV in the bubble, it is easily found that
$\unicode[STIX]{x1D708}_{p}$
denotes the phase velocity of the bubble. Considering similar energy gain around GeV in the bubble, it is easily found that
![]() $\unicode[STIX]{x1D708}_{e}=c\sqrt{1-\unicode[STIX]{x1D6FE}^{-2}}$
is rapidly close to the speed of light
$\unicode[STIX]{x1D708}_{e}=c\sqrt{1-\unicode[STIX]{x1D6FE}^{-2}}$
is rapidly close to the speed of light
![]() $c$
for electron energy larger than hundreds of MeV to GeV. However, for similar energy gain
$c$
for electron energy larger than hundreds of MeV to GeV. However, for similar energy gain
![]() $\unicode[STIX]{x0394}E$
the relativistic factor
$\unicode[STIX]{x0394}E$
the relativistic factor
![]() $\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D707}}=\unicode[STIX]{x0394}E/m_{\unicode[STIX]{x1D707}}+1$
of the muon is much smaller than that of electrons
$\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D707}}=\unicode[STIX]{x0394}E/m_{\unicode[STIX]{x1D707}}+1$
of the muon is much smaller than that of electrons
![]() $\unicode[STIX]{x1D6FE}_{e}=\unicode[STIX]{x0394}E/m_{e}+1$
since the muon is more massive than the electron by 207 resulting
$\unicode[STIX]{x1D6FE}_{e}=\unicode[STIX]{x0394}E/m_{e}+1$
since the muon is more massive than the electron by 207 resulting
![]() $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D707}}<\unicode[STIX]{x1D708}_{e}\approx c$
. Therefore, for the muon acceleration case the dephasing length reads
$\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D707}}<\unicode[STIX]{x1D708}_{e}\approx c$
. Therefore, for the muon acceleration case the dephasing length reads
where
![]() $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D707}}$
denotes the maximum velocity of muons. Therefore the dephasing length of muons is longer than that of electrons. Furthermore, the kinetic energy increase of charged particles in the rest frame of the bubble is
$\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D707}}$
denotes the maximum velocity of muons. Therefore the dephasing length of muons is longer than that of electrons. Furthermore, the kinetic energy increase of charged particles in the rest frame of the bubble is
![]() $\bar{E}R$
which is same for electrons and muons. Here
$\bar{E}R$
which is same for electrons and muons. Here
![]() $\bar{E}$
is the average acceleration field in the bubble. However, the kinetic energy increase of charged particles in the lab frame is
$\bar{E}$
is the average acceleration field in the bubble. However, the kinetic energy increase of charged particles in the lab frame is
 $$\begin{eqnarray}\unicode[STIX]{x0394}E=\frac{\bar{E}R+\unicode[STIX]{x1D708}_{p}p_{x}^{\prime }}{\sqrt{1-\frac{\unicode[STIX]{x1D708}_{p}^{2}}{c^{2}}}}=\unicode[STIX]{x1D6FE}\bar{E}R+\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D708}_{p}\sqrt{2m_{0}\bar{E}R},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x0394}E=\frac{\bar{E}R+\unicode[STIX]{x1D708}_{p}p_{x}^{\prime }}{\sqrt{1-\frac{\unicode[STIX]{x1D708}_{p}^{2}}{c^{2}}}}=\unicode[STIX]{x1D6FE}\bar{E}R+\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D708}_{p}\sqrt{2m_{0}\bar{E}R},\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6FE}=(1-\unicode[STIX]{x1D708}_{p}^{2}/c^{2})^{1/2}$
is the relativistic factor of the bubble and
$\unicode[STIX]{x1D6FE}=(1-\unicode[STIX]{x1D708}_{p}^{2}/c^{2})^{1/2}$
is the relativistic factor of the bubble and
![]() $p_{x}^{\prime }=\sqrt{2m_{0}\bar{E}R}$
is the momentum of the charged particle in the rest frame of the bubble. From Equation (5) we can find that the kinetic energy increase is strongly related to the invariant mass of the charged particle. Thus muons have higher energy gain compared to electrons on specific bubble setting.
$p_{x}^{\prime }=\sqrt{2m_{0}\bar{E}R}$
is the momentum of the charged particle in the rest frame of the bubble. From Equation (5) we can find that the kinetic energy increase is strongly related to the invariant mass of the charged particle. Thus muons have higher energy gain compared to electrons on specific bubble setting.
5 Summary
Therefore, compared to electron or proton laser plasma accelerations, this all-optical muon acceleration scheme has particular characteristics. For the massive invariant mass, muons could be injected into the whole bubble acceleration region with a broader energy spread. Furthermore, higher energy gain compared to electrons could be achieved from the longer dephasing length. On the other hand, the light invariant mass decreases the trapping energy threshold which makes muons easier to catch up the bubble. Considering the crucial requirement of laser intensity for proton acceleration in the laser wakefield discussed in Ref. [Reference Shen, Li, Yu and Cary31], muons (
![]() $\unicode[STIX]{x1D707}^{+}$
and
$\unicode[STIX]{x1D707}^{+}$
and
![]() $\unicode[STIX]{x1D707}^{-}$
) are the feasible choice besides the electron and positron in LWFA mechanism based on the short pulse laser facilities now. Additionally, as an unstable particle, muon’s lifetime
$\unicode[STIX]{x1D707}^{-}$
) are the feasible choice besides the electron and positron in LWFA mechanism based on the short pulse laser facilities now. Additionally, as an unstable particle, muon’s lifetime
![]() $2.2~\unicode[STIX]{x03BC}\text{s}$
multiplied by the relativistic factor is long enough compared to the production and acceleration processes proposed in our scheme. Thus the decay losses could be neglected unlike traditional accelerator based muon production and acceleration processes. It is worth to mention that traditional accelerator muon sources are also suitable for the discussion here, but high time synchronization precision is needed.
$2.2~\unicode[STIX]{x03BC}\text{s}$
multiplied by the relativistic factor is long enough compared to the production and acceleration processes proposed in our scheme. Thus the decay losses could be neglected unlike traditional accelerator based muon production and acceleration processes. It is worth to mention that traditional accelerator muon sources are also suitable for the discussion here, but high time synchronization precision is needed.
In conclusion, we propose a new all-optical ‘Generator and Booster’ scheme to accelerate muons from the Bethe–Heitler dimuon production process by the laser wakefield to supply a prompt, compact, low cost and controllable muon source in the laser laboratories. To our knowledge, it is the first research on muon acceleration in the laser wakefield. By applying a one-dimensional analytic model, the muon trapping energy threshold depending on the phase space of the bubble region is discussed in detail. A two-dimensional PIC simulation is carried out to validate the acceleration picture. The forward and backward muons in the bubble region are simulated and well agreement with the one-dimensional estimation is presented. We also extrapolate the estimation to higher energy muon acceleration. It is shown that a maximum energy up to 15.2 GeV could be achieved with an initial energy
![]() $E_{0}=1.45~\text{GeV}$
by accelerating muons for 300 ps with a bubble of relativistic factor
$E_{0}=1.45~\text{GeV}$
by accelerating muons for 300 ps with a bubble of relativistic factor
![]() $\unicode[STIX]{x1D6FE}=46$
. This fact seems quite promising on existing short pulse laser facilities[Reference Danson, Hillier, Hopps and Neely32]. We expect such a new all-optical ‘Generator and Booster’ muon source to be realized in the near future.
$\unicode[STIX]{x1D6FE}=46$
. This fact seems quite promising on existing short pulse laser facilities[Reference Danson, Hillier, Hopps and Neely32]. We expect such a new all-optical ‘Generator and Booster’ muon source to be realized in the near future.
Acknowledgements
The authors acknowledge Prof. H. B. Cai (IAPCM) for valuable discussions on this work. This work was supported by the Science Challenge Project (No. JCKY2016212A505) and the National Natural Science Foundation of China (No. 11805182).