Introduction
RINGS AND MODULES IN HONOUR OF PATRICK F. SMITH'S 65TH BIRTHDAY
-
- Published online by Cambridge University Press:
- 24 June 2010, pp. 1-5
-
- Article
-
- You have access
- Export citation
Research Article
BLOWUP FOR A DEGENERATE AND SINGULAR PARABOLIC EQUATION WITH NON-LOCAL SOURCE AND ABSORPTION*
-
- Published online by Cambridge University Press:
- 25 November 2009, pp. 209-225
-
- Article
-
- You have access
- Export citation
ALL NON-ARCHIMEDEAN NORMS ON K[X1, . . ., Xr]
-
- Published online by Cambridge University Press:
- 30 July 2009, pp. 1-18
-
- Article
-
- You have access
- Export citation
WEAKLY PERFECT GRAPHS ARISING FROM RINGS
-
- Published online by Cambridge University Press:
- 22 March 2010, pp. 417-425
-
- Article
-
- You have access
- Export citation
DECOMPOSITIONS OF COUNTABLE LINEAR TRANSFORMATIONS
-
- Published online by Cambridge University Press:
- 22 March 2010, pp. 427-433
-
- Article
-
- You have access
- Export citation
KOSTANT'S PROBLEM AND PARABOLIC SUBGROUPS
-
- Published online by Cambridge University Press:
- 30 July 2009, pp. 19-32
-
- Article
-
- You have access
- Export citation
SOBOLEV INEQUALITIES FOR ORLICZ SPACES OF TWO VARIABLE EXPONENTS
-
- Published online by Cambridge University Press:
- 25 November 2009, pp. 227-240
-
- Article
-
- You have access
- Export citation
POOR MODULES: THE OPPOSITE OF INJECTIVITY
-
- Published online by Cambridge University Press:
- 24 June 2010, pp. 7-17
-
- Article
-
- You have access
- Export citation
COMMON FIXED POINTS OF A PAIR OF NON-EXPANSIVE MAPPINGS WITH APPLICATIONS TO CONVEX FEASIBILITY PROBLEMS
-
- Published online by Cambridge University Press:
- 25 November 2009, pp. 241-252
-
- Article
-
- You have access
- Export citation
STRONGLY BOUNDED REPRESENTING MEASURES AND CONVERGENCE THEOREMS
-
- Published online by Cambridge University Press:
- 22 March 2010, pp. 435-445
-
- Article
-
- You have access
- Export citation
GOLDIE DIMENSION, DUAL KRULL DIMENSION AND SUBDIRECT IRREDUCIBILITY
-
- Published online by Cambridge University Press:
- 24 June 2010, pp. 19-32
-
- Article
-
- You have access
- Export citation
A NEIGHBOURHOOD CONDITION FOR GRAPHS TO BE FRACTIONAL (k, m)-DELETED GRAPHS*
-
- Published online by Cambridge University Press:
- 30 July 2009, pp. 33-40
-
- Article
-
- You have access
- Export citation
A GALOIS THEORY FOR THE FIELD EXTENSION K((X))/K
-
- Published online by Cambridge University Press:
- 25 August 2010, pp. 447-451
-
- Article
-
- You have access
- Export citation
THE MOMENTS OF MINKOWSKI QUESTION MARK FUNCTION: THE DYADIC PERIOD FUNCTION
-
- Published online by Cambridge University Press:
- 30 July 2009, pp. 41-64
-
- Article
-
- You have access
- Export citation
ALMOST-PERFECT MODULES
-
- Published online by Cambridge University Press:
- 24 June 2010, pp. 33-40
-
- Article
-
- You have access
- Export citation
φ-PRIME SUBMODULES
-
- Published online by Cambridge University Press:
- 25 November 2009, pp. 253-259
-
- Article
-
- You have access
- Export citation
ON DUAL BAER MODULES
-
- Published online by Cambridge University Press:
- 25 November 2009, pp. 261-269
-
- Article
-
- You have access
- Export citation
A GENERALISED KUMMER'S CONJECTURE
-
- Published online by Cambridge University Press:
- 25 August 2010, pp. 453-472
-
- Article
-
- You have access
- Export citation
SOME
 n−2 TERRACES FROM
n−2 TERRACES FROM  n POWER-SEQUENCES, n BEING AN ODD PRIME POWER
n POWER-SEQUENCES, n BEING AN ODD PRIME POWER
-
- Published online by Cambridge University Press:
- 30 July 2009, pp. 65-85
-
- Article
-
- You have access
- Export citation
GOLDIE*-SUPPLEMENTED MODULES
-
- Published online by Cambridge University Press:
- 24 June 2010, pp. 41-52
-
- Article
-
- You have access
- Export citation



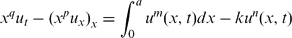
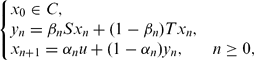
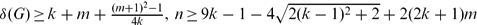 and
and 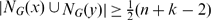 for each pair of non-adjacent vertices
for each pair of non-adjacent vertices 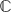
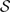
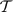
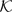

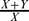 is small in
is small in 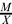 and
and 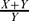 is small in
is small in 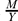 . We show that the β* relation is an equivalence relation and has good behaviour with respect to addition of submodules, homomorphisms and supplements. We apply these results to introduce the class of
. We show that the β* relation is an equivalence relation and has good behaviour with respect to addition of submodules, homomorphisms and supplements. We apply these results to introduce the class of