Research Article
A note on the conditional chromatic polynomial
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 265-267
-
- Article
-
- You have access
- Export citation
On the Arens semi-regularity of weighted group algebras
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 269-275
-
- Article
-
- You have access
- Export citation
Limits of covering spaces and residual properties of groups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 277-282
-
- Article
-
- You have access
- Export citation
On the Diophantine equation z2 = x4 + Dx2y2 + y4
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 283-285
-
- Article
-
- You have access
- Export citation
Wilson spaces and stable splittings of BTr
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 287-290
-
- Article
-
- You have access
- Export citation
On the non-albelian tensor square of a nilpotent group of class two
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 291-296
-
- Article
-
- You have access
- Export citation
Properties (V) and (u) are not three-space properties
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 297-299
-
- Article
-
- You have access
- Export citation
On quasi-permutation representations of finite groups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 301-308
-
- Article
-
- You have access
- Export citation
On dilation equations and the Hölder continuity of the de Rham functions
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 309-311
-
- Article
-
- You have access
- Export citation
Automorphism groups of complex doubles of Klein surfaces
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 313-330
-
- Article
-
- You have access
- Export citation
Local spectral theory and spectral inclusions
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 331-343
-
- Article
-
- You have access
- Export citation
Pure-semisimplicity is preserved under elementary equivalence
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 345-346
-
- Article
-
- You have access
- Export citation
Complete slices and homological properties of tilted algebras
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 347-354
-
- Article
-
- You have access
- Export citation
On stationary phase integrals
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 355-362
-
- Article
-
- You have access
- Export citation
Defining-relations for Hurwitz groups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 363-370
-
- Article
-
- You have access
- Export citation
Semigroup varieties closed for the Bruck extension
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 371-380
-
- Article
-
- You have access
- Export citation
Coranks of a quasi-projective module and its endomorphism ring
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 381-383
-
- Article
-
- You have access
- Export citation
Capitulation in unramified quadratic extensions of real quadratic number fields
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 385-392
-
- Article
-
- You have access
- Export citation
Front matter
GMJ volume 36 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f9
-
- Article
-
- You have access
- Export citation
Back matter
GMJ volume 36 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation



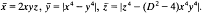 . It then follows that there are infinitely many such with (
. It then follows that there are infinitely many such with (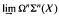 and let
and let 
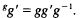 The tensor square is a special case of the nonabelian tensor product which has its origins in homotopy theory. It was introduced by R. Brown and J. L. Loday in [
The tensor square is a special case of the nonabelian tensor product which has its origins in homotopy theory. It was introduced by R. Brown and J. L. Loday in [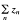 in
in 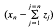 is weakly null. It is said that
is weakly null. It is said that 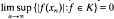 for every wuC series
for every wuC series 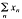 in
in 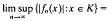 0 for every wuC series
0 for every wuC series 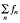 in
in 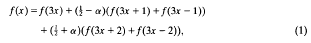

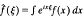 is the Fourier transform of
is the Fourier transform of 




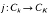
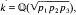 with distinct primes
with distinct primes