Research Article
On residually transcendental valued function fields of conics
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 137-145
-
- Article
-
- You have access
- Export citation
On linear recurrence sequences with polynomial coefficients
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 147-155
-
- Article
-
- You have access
- Export citation
On the theorem of Wójcik
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 157-162
-
- Article
-
- You have access
- Export citation
Finite co-Dedekindian groups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 163-169
-
- Article
-
- You have access
- Export citation
An extension of the Kegel–Wielandt theorem to locally finite groups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 171-176
-
- Article
-
- You have access
- Export citation
Boundaries of nonpositively curved groups of the form G × ℤn
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 177-189
-
- Article
-
- You have access
- Export citation
Models for joint isometries
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 191-194
-
- Article
-
- You have access
- Export citation
Solutions of Diophantine equations and divisibility of class numbers of complex quadratic fields
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 196-197
-
- Article
-
- You have access
- Export citation
A note on comonotonic additivity
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 199-205
-
- Article
-
- You have access
- Export citation
A nontrivial T1-space admitting a unique quasi-proximity
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 207-213
-
- Article
-
- You have access
- Export citation
Substitutional lemma for G-spaces of 1-dimensional groups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 215-220
-
- Article
-
- You have access
- Export citation
On the topological degree of real polynomial vector fields
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 221-231
-
- Article
-
- You have access
- Export citation
A note concerning the ideal of nuclear operators
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 233-236
-
- Article
-
- You have access
- Export citation
Strong bands of groups of left quotients
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 237-242
-
- Article
-
- You have access
- Export citation
Some remarks on regular Banach spaces
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 243-248
-
- Article
-
- You have access
- Export citation
Automorphic forms on nondiscrete Möbius groups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 249-253
-
- Article
-
- You have access
- Export citation
On a hyperlogistic delay equation
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 255-261
-
- Article
-
- You have access
- Export citation
Front matter
GMJ volume 38 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
GMJ volume 38 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation



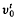 on the subfield
on the subfield 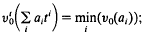 (ii)
(ii) 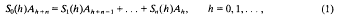
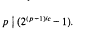
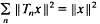 for all
for all 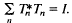 Athavale in [1] characterized the joint isometries as subnormal N-tuples whose minimal normal extensions have joint spectra in the unit sphere
Athavale in [1] characterized the joint isometries as subnormal N-tuples whose minimal normal extensions have joint spectra in the unit sphere 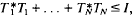 , can be represented as restrictions of certain weighted shifts direct sum a joint isometry. In this paper we adapt the canonical models of [3], and also construct a new canonical model, which completes the previous descriptions by showing joint isometries are indeed restrictions of specific multivariable weighted shifts [2].
, can be represented as restrictions of certain weighted shifts direct sum a joint isometry. In this paper we adapt the canonical models of [3], and also construct a new canonical model, which completes the previous descriptions by showing joint isometries are indeed restrictions of specific multivariable weighted shifts [2].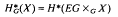
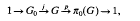
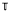 . We are dealing with the case in which π
. We are dealing with the case in which π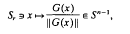
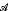 be a Banach algebra of bounded linear operators such that
be a Banach algebra of bounded linear operators such that 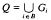 such that
such that 
 .
.