Hostname: page-component-8448b6f56d-jr42d Total loading time: 0 Render date: 2024-04-19T15:56:38.241Z Has data issue: false hasContentIssue false
  • English
  • Français

THE YONEDA EXT AND ARBITRARY COPRODUCTS IN ABELIAN CATEGORIES

Part of: Abelian categories Homological algebra General theory of categories and functors

Published online by Cambridge University Press:  19 March 2021

ALEJANDRO ARGUDÍN-MONROY
ALEJANDRO ARGUDÍN-MONROY*
Affiliation:
Instituto de Matemáticas, Universidad Nacional Autónoma de México, Circuito Exterior, Ciudad Universitaria, C.P.04510 Mexico City, Mexico e-mail: argudin@ciencias.unam.mx
Get access Rights & Permissions [Opens in a new window]

Abstract

There are well-known identities involving the Ext bifunctor, coproducts, and products in AB4 abelian categories with enough projectives. Namely, for every such category 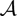\[\mathcal{A}\], given an object X and a set of objects 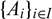\[{\{ {{\text{A}}_{\text{i}}}\} _{{\text{i}} \in {\text{I}}}}\], an isomorphism 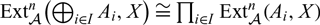\[Ext_\mathcal{A}^{\text{n}}({ \oplus _{{\text{i}} \in {\text{I}}}}{{\text{A}}_{\text{i}}},{\text{X}}) \cong \prod\nolimits_{{\text{i}} \in {\text{I}}} {Ext_\mathcal{A}^{\text{n}}({{\text{A}}_{\text{i}}},{\text{X}})} \] can be built, where 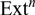\[Ex{t^{\text{n}}}\] is the nth derived functor of the Hom functor. The goal of this paper is to show a similar isomorphism for the nth Yoneda Ext, which is a functor equivalent to 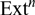\[Ex{t^{\text{n}}}\] that can be defined in more general contexts. The desired isomorphism is constructed explicitly by using colimits in AB4 abelian categories with not necessarily enough projectives nor injectives, extending a result by Colpi and Fuller in [8]. Furthermore, the isomorphisms constructed are used to characterize AB4 categories. A dual result is also stated.

MSC classification

Primary: 18G15: Ext and Tor, generalizations, Künneth formula 18E10: Exact categories, abelian categories
Secondary: 18E99: None of the above, but in this section 18A30: Limits and colimits (products, sums, directed limits, pushouts, fiber products, equalizers, kernels, ends and coends, etc.)
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 64 , Issue 2 , May 2022 , pp. 277 - 291
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The author thanks the Project PAPIIT-Universidad Nacional Autónoma de México IN100520.

References

Baer, R., Erweiterung von Gruppen und ihren Isomorphismen, Mathematische Zeitschrift 38(1) (1934), 375–416.CrossRefGoogle Scholar
Baer, R., Automorphismen von Erweiterungsgruppen (Hermann, Paris, 1935).Google Scholar
Becerril, V., Mendoza, O. and Santiago, V., Relative Gorenstein objects in abelian categories, Commun. Algebra 49(1) (2021), 352–402.CrossRefGoogle Scholar
Brauer, R., Untersuchungen über die arithmetischen Eigenschaften von Gruppen linearer Substitutionen I, Mathematische Zeitschrift 28(1) (1928), 677–696.CrossRefGoogle Scholar
Buchsbaum, D. A., A note on homology in categories, Ann. Math. 69 (1959), 66–74.CrossRefGoogle Scholar
Butler, M. C. R. and Horrocks, G., Classes of extensions and resolutions, Philos. Trans. R. Soc. London 254(1039) (1961), 155–222.Google Scholar
Cartan, H. and Eilenberg, S., Homological algebra (The Princeton University Press, Princeton, 1956).Google Scholar
Colpi, R. and Fuller, K., Tilting objects in abelian categories and quasitilted rings, Trans. Am. Math. Soc. 359(2) (2007), 741–765.CrossRefGoogle Scholar
Čoupek, P. and Št’ovček, J., Cotilting sheaves on noetherian schemes, Mathematische Zeitschrift 296 (2020), 275–312.CrossRefGoogle Scholar
Eilenberg, S. and MacLane, S., Group extensions and homology, Ann. Math. 43 (1942), 757–831.CrossRefGoogle Scholar
Freyd, P. J., Abelian categories, vol. 1964 (Harper & Row, New York, 1964).Google Scholar
Grothendieck, A., Sur quelques points d’algèbre homologique, Tohoku Math. J. Second Ser. 9(2) (1957), 119–183.Google Scholar
Hasse, H., Noether, E. and Brauer, R., Beweis eines Hauptsatzes in der Theorie der Algebren, Journal für die reine und angewandte Mathematik 1932(167) (1932), 399–404.Google Scholar
Hilton, P. J. and Stammbach, U., A course in homological algebra, vol. 4 (Springer, New York, 2012).Google Scholar
Hölder, O., Die Gruppen, der Ordnungen p 3, pq 2, pqr, p 4 , Mathematische Annalen 43 (1893), 301–412.CrossRefGoogle Scholar
MacLane, S., Homology (Springer-Verlag, Berlin & Heidelberg, 1963).CrossRefGoogle Scholar
Mitchell, B., Theory of categories (Academic Press, New York & London, 1965).Google Scholar
Popescu, N., Abelian categories with applications to rings and modules (Academic Press, London & New York, 1973).Google Scholar
Positselski, L. and Št’ovček, J., The tilting–cotilting correspondence, Int. Math. Res. Not. 2021(1) (2021), 189–274.CrossRefGoogle Scholar
Schreirer, O., Über die Erweiterungen von Gruppen I, Monatshefte für Mathematik und Physik 34 (1926), 165–180.CrossRefGoogle Scholar
Stenström, B., Rings of quotients. An introduction to methods of ring theory, vol. 217 (Springer-Verlag, Berlin & Heidelberg, 1975).Google Scholar
Yoneda, N., On the homology theory of modules, J. Fac. Sci. Univ. Tokyo 7 (1954), 193–227.Google Scholar
Yoneda, N., On ext and exact sequences, J. Fac. Sci. Univ. Tokyo 8 (1960), 507–526.Google Scholar