Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
EWENS, W.J.
and
FELDMAN, M.W.
1976.
Population Genetics and Ecology.
p.
303.
Holgate, P.
1976.
Direct products of genetic algebras and Markov chains.
Journal of Mathematical Biology,
Vol. 3,
Issue. 3-4,
p.
289.
Lichter, Robert
1976.
Progress in Botany / Fortschritte der Botanik.
p.
230.
Ewens, Warren J.
1977.
Advances in Human Genetics 8.
p.
67.
Cadien, James D.
Hassett, Matthew J.
and
Friedlaender, Jonathan S.
1978.
Linkage disequilibrium in Bougainville Island.
American Journal of Physical Anthropology,
Vol. 48,
Issue. 3,
p.
297.
Hedrick, Philip
Jain, Subodh
and
Holden, Larry
1978.
Evolutionary Biology.
p.
101.
Campbell, R. B.
1980.
The effect of migration and recombination on the equilibrium structure of populations subject to a common symmetric selection regime.
Genetical Research,
Vol. 36,
Issue. 1,
p.
29.
Jorde, Lynn B.
1980.
Current Developments in Anthropological Genetics.
p.
135.
Clark, A G
and
Feldman, M W
1981.
Disequilibrium between linked inversions: an alternative hypothesis.
Heredity,
Vol. 46,
Issue. 3,
p.
379.
Østergaard, Hanne
and
Christiansen, Freddy Bugge
1981.
Selection component analysis of natural polymorphisms using population samples including mother-offspring combinations, II.
Theoretical Population Biology,
Vol. 19,
Issue. 3,
p.
378.
Barton, N H
1986.
The effects of linkage and density-dependent regulation on gene flow.
Heredity,
Vol. 57,
Issue. 3,
p.
415.
Wynn, Addison H.
1986.
LINKAGE DISEQUILIBRIUM AND A CONTACT ZONE IN
PLETHODON CINEREUS
ON THE DEL‐MAR‐VA PENINSULA
.
Evolution,
Vol. 40,
Issue. 1,
p.
44.
Christiansen, Freddy Bugge
1987.
The deviation from linkage equilibrium with multiple loci varying in a stepping-stone cline.
Journal of Genetics,
Vol. 66,
Issue. 1,
p.
45.
BARKER, J. S. F.
EAST, P. D.
and
CHRISTIANSEN, F. B.
1989.
Estimation of migration from a perturbation experiment in natural populations of Drosophila buzzatii Patterson & Wheeler.
Biological Journal of the Linnean Society,
Vol. 37,
Issue. 4,
p.
311.
Christiansen, Freddy Bugge
1990.
Mathematical and Statistical Developments of Evolutionary Theory.
p.
121.
Asmussen, Marjorie A.
and
Arnold, Jonathan
1991.
The effects of admixture and population subdivision on cytonuclear disequilibria.
Theoretical Population Biology,
Vol. 39,
Issue. 3,
p.
273.
Yang, R.-C.
and
Yeh, F. C.
1993.
Multilocus structure in Pinus contorta Dougl..
Theoretical and Applied Genetics,
Vol. 87,
Issue. 5,
p.
568.
Epperson, Bryan K.
1993.
Evolutionary Biology.
p.
95.
Tachida, Hidenori
1994.
Decay of linkage disequilibrium in a finite island model.
Genetical Research,
Vol. 64,
Issue. 2,
p.
137.
Navarro, Arcadio
Betrán, Esther
Zapata, Carlos
and
Ruiz, Alfredo
1996.
Dynamics of gametic disequilibria between loci linked to chromosome inversions: the recombination-redistributing effect of inversions.
Genetical Research,
Vol. 67,
Issue. 1,
p.
67.
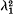 , where λ1 is the rate of convergence of the gene frequencies to equilibrium and c is the recombination frequency. In the second model at equilibrium there will be a linear cline in gene frequencies connecting the two large constant populations. This cline will be accompanied by a ‘cline’ of linkage disequilibria. The rate of convergence to this equilibrium cline is independent of the recombination frequency, and, in fact, the gene frequencies and the linkage disequilibria converge to equilibrium at the same rate.
, where λ1 is the rate of convergence of the gene frequencies to equilibrium and c is the recombination frequency. In the second model at equilibrium there will be a linear cline in gene frequencies connecting the two large constant populations. This cline will be accompanied by a ‘cline’ of linkage disequilibria. The rate of convergence to this equilibrium cline is independent of the recombination frequency, and, in fact, the gene frequencies and the linkage disequilibria converge to equilibrium at the same rate.

