1. Introduction
Although mutation is the ultimate source of polygenic variation, i.e., the raw material for the maintenance of genetic variability (Hill, Reference Hill1982b), little is known about its role and real contribution to the genetic variability in mammals. Previous analyses characterized this phenomenon in terms of the mutational input of genetic variance per generation (σ m 2 ), a well-defined genetic parameter contributing less than 1% of the phenotypic variance (Lynch, Reference Lynch1988; Houle et al., Reference Houle, Morikawa and Lynch1996). Although polygenic mutational studies have mainly been conducted on invertebrate laboratory species (Hill, Reference Hill1982a; Caballero et al., Reference Caballero, Toro and López-Fanjul1991), the relevant contribution of σ m 2 on the phenotypic variance of quantitative traits has also been described in mice (Bailey, Reference Bailey1959; Festing, Reference Festing1973; Keightley & Hill, Reference Keightley and Hill1992; Caballero et al., Reference Caballero, Keightley and Hill1995) and sheep (Casellas et al., Reference Casellas, Caja and Piedrafita2010). Nevertheless, these σ m 2 estimates cannot be considered as biologically irrelevant, as demonstrated by the successful response to artificial selection reported in some highly inbred lines (Hill, Reference Hill1982a, Reference Hill2005; Keightley, Reference Keightley1998). Recent results focused on the accumulation of within-generation mutational variability revealed a remarkable source of additive genetic variability representing up to 4% of the phenotypic variance for litter size in inbred mice (Casellas & Medrano, Reference Casellas and Medrano2008).
The effect of new mutations cannot be simplified to only accounting for a direct additive contribution of the gene itself, but it must also account for important novel epistatic interactions between genes. Our knowledge on physiological genetics strongly suggests that interaction among gene products is ubiquitous (Wright, Reference Wright1980). New mutations must be part of this epistatic component although research has not been conducted in this field. The contribution of epistasis to genetic variance components remains obscure due to methodological complexities (Crow & Kimura, Reference Crow and Kimura1970; Goodnight, Reference Goodnight1987, Reference Goodnight1988; Wade, Reference Wade1992; Cheverud & Routman, Reference Cheverud and Routman1995) and the limited contribution of epistasis to the covariance among relatives (Cockerham, Reference Cockerham1954; Hayman & Mather, Reference Hayman and Mather1955; Falconer, Reference Falconer1989). Experimental results remain controversial (Simons & Crow, Reference Simons and Crow1977; Barker, Reference Barker1979), although some studies have reported large contributions to the phenotypic variance (Peripato et al., Reference Peripato, de Brito, Matioli, Pletscher, Vaughn and Cheverud2005; Leamy et al., Reference Leamy, Pomp and Lightfoot2008), they account for more than 25% of the variability. In any case, the influence of new mutations was not considered in these studies and thus, the epistatic contribution linked to the continuous uploading of new mutations variance remains unknown.
A basic assumption in studies involving inbred strains of laboratory species is that inbred individuals are genetically homogeneous across generations (Taft et al., Reference Taft, Davisson and Wiles2006; Stevens et al., Reference Stevens, Banks, Festing and Fisher2007). In addition to the direct additive variability generated by mutation (Niu & Liang, Reference Niu and Liang2009), the genetic homogeneity can be seriously impaired if new mutational epistasis had a relevant contribution to the phenotypic variability of any quantitative trait of interest. In addition, the study of mutational epistasis contributes information relevant to livestock production systems where both non-additive contributions and mutational additive effects were recently revealed (Casellas et al., Reference Casellas, Caja and Piedrafita2010; Su et al., Reference Su, Christensen, Ostersen, Henryon and Lund2012).
The study of mutational epistatic effects opens an interesting research field within the context of animal genomics with potential implications for both basic genetics research and applied animal production. The purpose of the present investigation was to analyse epistatic interactions between new mutational additive genetic effects and the genetic background inherited from the founder populations, taking body weight of two mice data sets as example. An appropriate linear mixed model parameterization was developed to properly account for the different genetic sources of variation, and the model was solved by Bayesian inference.
2. Materials and methods
(i) Mice data sets
This research focused on the genetic interaction between founder-related additive polygenic effects and new additive genetic variability arising from mutation. Within-generation founder-related additive genetic variance decreases with the number of generations in inbred mice, these variances becoming almost null after a few generations of full-sib mating (Casellas & Medrano, Reference Casellas and Medrano2008; Casellas et al., Reference Casellas, Caja and Piedrafita2010). In order to avoid biases due to the absence of founder-related additive genetic variance in more recent generations, our analyses was performed on subsets of mouse data spanning few (five or six) generations, although with a large number of mice per generation. These restrictions provided large founder populations where the additive genetic variance was properly assessed (Table 1). On the other hand, contribution of epistasis is typically assumed small and absorbed into the founder-related additive genetic component (Cheverud & Routman, Reference Cheverud and Routman1995; Hill et al., Reference Hill, Goddard and Visscher2008; Crow, Reference Crow2010). Note that founder-specific genetic variance must be clearly smaller in these highly inbred populations than in regular populations, allowing for a more efficient differentiation between both sources of genetic variance. Although confusion between epistasis and other sources of additive genetic variability cannot be completely discarded, final estimates must be seen as minimum boundaries for epistasis in these populations.
Table 1. Summary of pedigree and phenotypic data for the two mice data sets, B6 and B6hghg
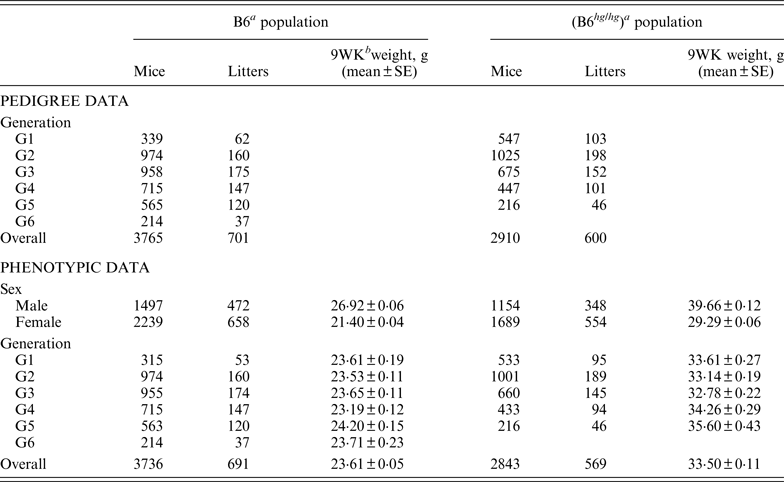
a B6 (C57BL/6J), B6 hg/hg (C57BL/6J-hghg, B6 mice introgressed with the high growth mutation).
b 9WK weight: body weight at 9 weeks of age.
SE: Standard error.
As described by Casellas & Medrano (Reference Casellas and Medrano2008), a C57BL/6J (B6) inbred mouse strain was kept in the vivarium of the University of California (Davis, CA) between October 1988 and May 2005. This population was founded by the acquisition of two B6 males and six B6 females from The Jackson Laboratory (Bar Harbor, ME) and evolved during 46 non-overlapping generations. Our analyses focused on a B6 subpopulation derived and expanded from mice born in the 21st generation (Table 1, generation G1) and maintained during five non-overlapping generations (Table 1, generations G2 to G6) without additional contributions from the main B6 line or other outside populations. Whereas the main B6 line was maintained with a reduced number of litters per generation (five to 47 litters), this subpopulation involved 701 litters and 3765 mice in a short period of six generations. Mice were housed in polycarbonate cages under controlled temperature (21°C ± 2°C), humidity (40–70%) and lighting (14 hr light, 10 hr dark, lights on at 7 a.m.) conditions and managed according to the guidelines of the American Association for Accreditation of Laboratory Animal Care (http://www.aaalac.org). Only single (one male/one female) and group matings (one male/several females) were used to avoid multiple paternities. Females were housed in individual cages for parturition. Full-sib mating was preferentially used to propagate the population. Pups were individually numbered by ear notching at 2 weeks of age. After weaning (3 weeks) male and female pups were housed in separate cages to avoid uncontrolled matings. Mice were weighted 9 weeks (±2 days) after birth (9WK body weight). All relevant data were recorded accurately in all generations. Sire, dam, dates of mating, birth and weaning, number of pups born and weaned were recorded for each litter, and identification number, sex and 9WK body weight were recorded for each mouse. Analyses were performed on 3736 mice with 9WK body weight data coming from 691 litters, whereas the pedigree file included 3765 mice with a complete knowledge of all parental and maternal relationships.
On the other hand, the high growth (hg) mutation spontaneously arose in a four-way cross involving AKR/J, C3H, C57BL/6J and DBA/2 inbred founders (Bradford, Reference Bradford1971; Bradford & Famula, Reference Bradford and Famula1984), and was introgressed into the B6 background (B6 hg/hg ) in 1981 (Bradford & Famula, Reference Bradford and Famula1984). This mutation, a 500 kb deletion on mouse chromosome 10 (Horvat & Medrano, Reference Horvat and Medrano2001; Wong et al., Reference Wong, Islas-Trejo and Medrano2002), deregulates the growth hormone/insulin-like growth factor 1 system (Medrano et al., Reference Medrano, Pomp, Sharrow, Bradford, Downs and Frohman1991) and produces a 30–50% post-weaning overgrowth without increasing adiposity (Bradford & Famula, Reference Bradford and Famula1984; Corva & Medrano, Reference Corva and Medrano2000). Note that the B6 hg/hg strain was isogenic to B6, except for the hg mutation and a stretch of AKR/J sequence around this mutation (Horvat & Medrano, Reference Horvat and Medrano1996). The B6 hg/hg strain has been maintained for experimental purposes in our vivarium at the University of California (Davis, CA) during more than 150 generations and 5000 litters. Although the number of litters per generation was generally small, our analyses focused on a five-generations expansion of this B6 hg/hg strain generated between years 1996 and 1997, involving between 46 and 198 litters per generation (Table 1). Animal husbandry and data collection followed the same procedures defined for the B6 population. Analyses were performed on a pedigree 2910 mice, 2843 of them having 9WK body weight phenotypic information (Table 1).
(ii) Statistical models
After appropriate edition, 9WK body weight in B6 and B6 hg/hg data sets was modelled under the following hierarchical structure:
where e was the column vector of random errors and y was the column vector of phenotypic data linked to systematic (b), permanent environmental (p) and genetic effect (a, m and a × m) by X, Z 1 and Z 2 incidence matrices, respectively. Note that the genetic sources of variation were defined as the additive genetic effect linked to the base generation (a; founder-related additive genetic effect), the new additive variability originated by mutation (m; see Wray (Reference Wray1990) for a detailed description of this genetic effect), and the epistatic interaction between both terms (a × m). Systematic effects accounted for sex (male or female) and generation number with six and five levels for B6 and B6 hg/hg populations, respectively. The permanent environmental effect was defined as the environmental contribution inherent to each group of mice kept in the same cage after weaning.
Our analyses focused on several aspects of the genetic background for WK9 body weight in mice, requiring an accurate specification of the distribution pattern for a, m and a × m Assuming an infinitesimal polygenic genetic architecture (Bulmer, Reference Bulmer1980), a can be assumed to be drawn from a multivariate normal distribution as follows:
where A is the numerator relationship matrix as defined by Wright (Reference Wright1922), σ a 2 is the additive genetic variance component and 0 is a column vector or zeros. Following Wray (Reference Wray1990) theoretical developments for new additive mutational variability, m can be modelled under the following multivariate normal distribution:
where M is the Casellas & Medrano (Reference Casellas and Medrano2008) numerator relationship matrix adapted from Wray (Reference Wray1990) to accommodate new additive mutations, and σ m 2 is the mutational variance. The a × m effect is approximated as the additive epistatic interaction between founder-related and new mutational effects on the basis of Cockerham's (Reference Cockerham1954) model. This interaction is assumed to be sampled from:
where H is the Hadamard product between matrices A and M, and σ i 2 is the interaction (or epistasis) variance. Note that this parameterization applied to populations under Hardy–Weinberg equilibrium (Hardy, Reference Hardy1908; Weinberg, Reference Weinberg1908), whereas these inbred populations were maintained under assorted mating of full-sibs. Nevertheless, this must be viewed as a reasonable equilibrium between biological plausibility and mathematical parameterization. The main complexity of this parameterization relies on the inversion of covariance matrices (A −1, M −1 and H −1), an essential step for the proper construction of the mixed model equations (Henderson, Reference Henderson1973). Matrices A −1 and M −1 converge to a well-known structure that can be constructed with low computational requirements from a list of parents (Henderson, Reference Henderson1976; Quaas, Reference Quaas1976; Wray, Reference Wray1990; Casellas & Medrano, Reference Casellas and Medrano2008), without requiring direct matrix inversion. Conversely, we lacked the simplified rules for constructing H −1 and the direct inversion of H becomes mandatory, resulting in high computational time requirements for medium to large populations. Although these computational demands for obtaining H −1 would not be a decisive limitation for our analyses, alternative parameterizations avoiding the direct inversion of H could be of special interest for larger data sets.
The previous hierarchical mixed model can be rewritten as follows:
where i = H−1 (a × m), the new interaction term i comes from a multivariate normal distribution:
and only (H −1)−1 = H is required for the proper construction of the mixed model equations. This alternative parameterization of the mixed model equations was described by Henderson (Reference Henderson1984), although under standard genetic evaluation models. Note that H can be constructed from A and M, and both A and M are obtained by the tabular method (Wright, Reference Wright1922) or other computationally efficient approaches. After obtaining i, the a × m term can be calculated in a straightforward manner by applying the following relationship:
It is important to note that the variance component (σ i 2 ) does not undergo any modification during this reparameterization, leading to a direct calculation of the heritability for additive epistatic effects (h i 2 ; i.e., the percentage of total phenotypic variance accounted for by σ i 2 ) as follows:
Both additive (h a 2 ) and mutational (h m 2 ) heritabilities can be calculated in a similar way by appropriately replacing the numerator σ i 2 by σ a 2 and σ m 2 , respectively. Despite current parameterization assuming null genetic correlations between a, m and a × m, we must be cautious because breeding values become linear functions of mutation effects (Wray, Reference Wray1990); collinearity must be evaluated among the genetic effects included in the model in order to determine their robustness and accuracy. Within this context, Pearson correlation coefficients were computed between each pairwise combination of a, m, a × m and e, and their posterior distributions were evaluated as indicators of relatedness between genetic effects. High and positive correlations would suggest a high degree of collinearity, whereas null or almost null estimates must indicate independence.
(iii) Bayesian analyses
Within a Bayesian development, the joint posterior distribution of our model was proportional to the likelihood of the data multiplied by the a priori probabilities of the unknown parameters of the model:
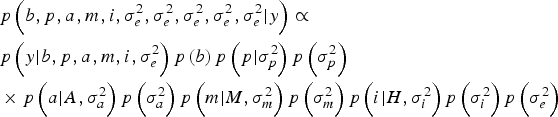 $$\eqalign{& p\left(b,p,a,m,i,\sigma_e^{2}, \sigma_e^{2}, \sigma_e^{2}, \sigma_e^{2}, \sigma_e^{2} | y \right) \propto \cr & p\left(y| b,p,a,m,i,\sigma _e^{2} \right)p\left(b \right)p\left(p| \sigma_p^{2} \right)p\left(\sigma_p^{2} \right) \cr & \times p\left(a| A,\sigma _a^{2} \right)p\left(\sigma_a^{2} \right)p\left(m| M,\sigma_m^{2} \right)p\left(\sigma_m^{2} \right)p\left(i| H,\sigma_i^{2} \right)p\left(\sigma_i^{2} \right)p\left(\sigma_e^{2} \right)} $$
$$\eqalign{& p\left(b,p,a,m,i,\sigma_e^{2}, \sigma_e^{2}, \sigma_e^{2}, \sigma_e^{2}, \sigma_e^{2} | y \right) \propto \cr & p\left(y| b,p,a,m,i,\sigma _e^{2} \right)p\left(b \right)p\left(p| \sigma_p^{2} \right)p\left(\sigma_p^{2} \right) \cr & \times p\left(a| A,\sigma _a^{2} \right)p\left(\sigma_a^{2} \right)p\left(m| M,\sigma_m^{2} \right)p\left(\sigma_m^{2} \right)p\left(i| H,\sigma_i^{2} \right)p\left(\sigma_i^{2} \right)p\left(\sigma_e^{2} \right)} $$
The likelihood of WK9 body weight data was defined as multivariate normal:
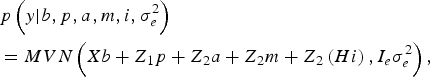 $$\eqalign {& p\left( y| b,p,a,m,i,\sigma _e^{2} \right) \cr &= MVN\left(Xb + Z_1 p + Z_{2} a + Z_{2} m + Z_{2} \left(Hi \right), I_e \sigma_e^{2} \right),}$$
$$\eqalign {& p\left( y| b,p,a,m,i,\sigma _e^{2} \right) \cr &= MVN\left(Xb + Z_1 p + Z_{2} a + Z_{2} m + Z_{2} \left(Hi \right), I_e \sigma_e^{2} \right),}$$
With I e being an identity matrix with dimensions equal to the number of phenotypic data. The a priori distribution of P was assumed to be drawn from another multivariate normal density:
Where I p is an identity matrix with dimensions equal to the number of elements in P, and the genetic effects (a, m and a × m) were modelled under the multivariate normal distributions previously defined in the earlier sections of this manuscript. Flat priors were assumed for b, σ e 2 and σ p 2 . To evaluate the effect of a priori information on σ a 2 , σm 2 and σ i 2 , four different scaled inverted χ 2 prior distributions with hyperparameters ν and S 2 were assumed (Fig. 1) and tested independently on our data sets (see below). Given the almost null previous knowledge about the expected distribution of σ a 2 , σ m 2 and σ i 2 , these four independent scaled χ –2 priors depicted a wide range of plausible scenarios with a decreasing level of stringency for the distribution of the variance component. Whereas prior 1 (ν = 10; S 2 = 0·1) has a narrow probability close to the null estimate, prior 4 (ν = −2; S 2 = 0) converged to uniform distribution between 0 and + ∞, ignoring previous knowledge and providing the same a priori probability to all values within the parametric space.
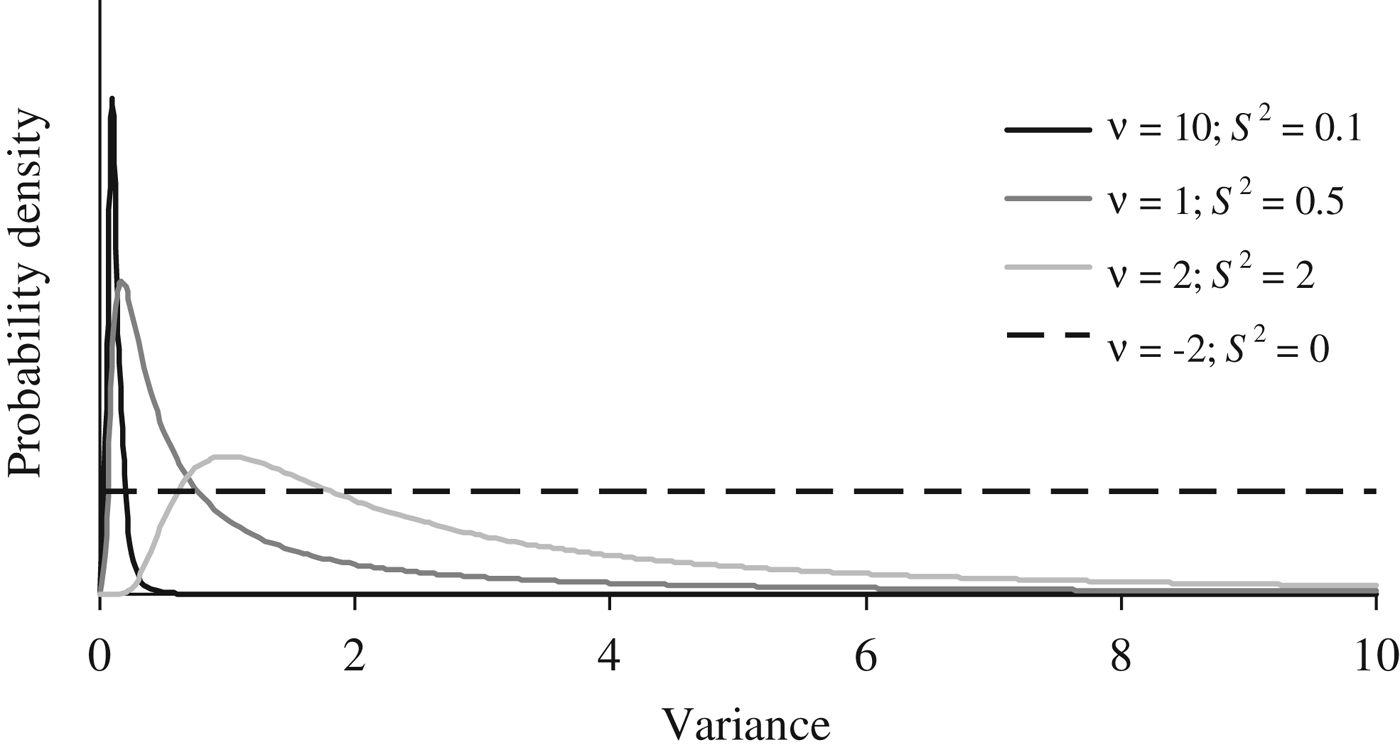
Fig. 1. A priori distributions for genetic variance components analyzed using scaled χ −2 priors with hyperparameters ν = 10 and S 2 = 0·1 (PR1), ν = 1 and S 2 = 0·5 (PR2), ν = 2 and S 2 = 2.
In order to elucidate the biological and statistical relevance of the additive genetic effects, analyses were performed under a three-step approach (see below). During this process, the statistical performance of all models was evaluated and compared in terms of goodness of fit and predictive ability. The first comparison, i.e., goodness of fit, was carried out by the deviance information criterion (DIC), a Bayesian statistic integrating information from both models fit to real data and mathematical complexity in terms of number of parameters (Spiegelhalter et al., Reference Spiegelhalter, Best, Carlin and van der Linde2002). Models with smaller DIC were favoured as this indicated a better model fit and a lower degree of model complexity. Differences larger than 3–5 DIC units are typically assumed as relevant (Spiegelhalter et al., Reference Spiegelhalter, Best, Carlin and van der Linde2002, Reference Spiegelhalter, Thomas, Best and Lunn2003). On the other hand, the prediction of future records given past data is a question of concern that can be answered using the concept of predictive density, a notion that arises naturally in Bayesian statistics (Matos et al., Reference Matos, Thomas, Gianola, Pérez-Enciso and Young1997). To estimate predictive ability, a new data set was generated by removing 50% of the records. Both mean square error (MSE) and correlation coefficient (
![]() $\rho _{y,\tilde y} $
) were computed between expectations from the predictive distribution and the removed records (see Casellas et al. (Reference Casellas, Caja, Ferret and Piedrafita2007) for a detailed description of the calculation of MSE and
$\rho _{y,\tilde y} $
) were computed between expectations from the predictive distribution and the removed records (see Casellas et al. (Reference Casellas, Caja, Ferret and Piedrafita2007) for a detailed description of the calculation of MSE and
![]() $\rho _{y,\tilde y} $
).
$\rho _{y,\tilde y} $
).
During the first step, a reference model without additive genetic effects (Model 0) was analysed. This model assumed the same hierarchical structure and a priori distributions defined for the complex model described above, although arbitrarily fixing a, m and a × m effects to 0. During the second analytical step, Model 0 was complemented with the inclusion of the a and m effects as unknown parameters of the model (Model AM), although the a × m term was still fixed to 0. Following Casellas & Medrano (Reference Casellas and Medrano2008), the same a priori distribution was assumed for σ
a
2
and σ
m
2
and therefore, four different parameterizations were analysed assuming priors 1, 2, 3 and 4 (Fig. 1). Finally, the Model AM with the smallest DIC value evolved to the inclusion of the a × m as an additional effect to be estimated (Model E). As for the previous step, the four-scaled inverted χ
2-prior distributions for σ
i
2
were evaluated by four independent analyses. At the end, nine different models were analysed and compared by the DIC, MSE and
![]() $\rho _{y,\tilde y} $
parameters.
$\rho _{y,\tilde y} $
parameters.
For each model and data set, three independent Monte Carlo Markov chains (MCMC) were launched for sampling for the marginal posterior distribution of each unknown parameter in our analyses. All parameters were updated by Gibbs sampling (Gelfand & Smith, Reference Gelfand and Smith1990) and each MCMC was composed of 1 050 000 iterations. Chain convergence was checked by visual inspection of σ i 2 plots (or σ m 2 for Model 0) and by the Raftery & Lewis (Reference Raftery, Lewis, Bernardo, Berger, Dawid and Smith1992) method. Although convergence was reached with less than 1000 iterations in all MCMC, the first 50 000 iterations were discarded. Given the autocorrelation inherent to the successive iterations of Gibbs sampling, only one iteration from each 50 iterations was stored for inference purposes. The posterior distribution of each parameter was constructed with 20 000 values from each of the three MCMC evoking the ergodic property of the chains (Gilks et al., Reference Gilks, Richardson and Spiegelhalter1996).
3. Results
(i) Phenotypic data
The phenotypic characterization of the two mouse inbred strains were the starting point for the characterization of the genetic sources of variation. Average 9WK body weight phenotypic values for B6 and B6 hg/hg strains are shown on Table 1. B6 hg/hg mice were 9·89 g heavier than B6 mice on average (p < 0·001) and, in a similar way, its raw phenotypic variability increased to 34·40 g2; note that the phenotypic dispersion for the B6 population was 9·34 g2. Males were heavier than females in both B6 (+5·52 g; p = 0·001) and B6 hg/hg (+10·37 g; p = 0·001) strains and within-generation averages were moderately heterogeneous, providing few differences at p = 0·05. Note that both mouse sex and generation were properly accounted for in the mixed linear models used in this study.
(ii) Model comparison
Model 0 lacked additive genetic effects and it was assumed as the starting reference stage for our analyses. This model reached an average DIC value of 13 767·7 and 13 810·0 for B6 and B6
hg/hg
mice, respectively (Tables 2
a and 2
b); moreover, this model also provided maximum estimates for MSE and minimum estimates for
![]() $\rho _{y,\tilde y} $
when compared with remaining models. Note that these values did not provide information by themselves, but alternative models provide the base to compare remaining estimates. The inclusion of the a and m effects generalized Model 0 to a model accounting for direct additive genetic effects (model AM). Given the decreasing degree of stringency evoked by the a priori distributions assumed for σ
a
2
and σ
m
2
variances (Fig. 1), the effect of four alternative stages of a priori knowledge on the expected values of both variance components were evaluated. Assuming that 3 to 5 DIC units are the minimal departure to report significant differences between two competing models (Spiegelhalter et al., Reference Spiegelhalter, Best, Carlin and van der Linde2002, 2003), Model AM4 was clearly preferred when compared with the null hypothesis characterized by Model 0, as demonstrated by the 395·2 and 291·3 DIC units reduction in B6 and B6
hg/hg
populations, respectively. The other three parameterizations of Model AM (priors 1, 2 and 3) were slightly penalized (Tables 2
a and 3
a) in relation to Model AM4, although DIC, MSE and
$\rho _{y,\tilde y} $
when compared with remaining models. Note that these values did not provide information by themselves, but alternative models provide the base to compare remaining estimates. The inclusion of the a and m effects generalized Model 0 to a model accounting for direct additive genetic effects (model AM). Given the decreasing degree of stringency evoked by the a priori distributions assumed for σ
a
2
and σ
m
2
variances (Fig. 1), the effect of four alternative stages of a priori knowledge on the expected values of both variance components were evaluated. Assuming that 3 to 5 DIC units are the minimal departure to report significant differences between two competing models (Spiegelhalter et al., Reference Spiegelhalter, Best, Carlin and van der Linde2002, 2003), Model AM4 was clearly preferred when compared with the null hypothesis characterized by Model 0, as demonstrated by the 395·2 and 291·3 DIC units reduction in B6 and B6
hg/hg
populations, respectively. The other three parameterizations of Model AM (priors 1, 2 and 3) were slightly penalized (Tables 2
a and 3
a) in relation to Model AM4, although DIC, MSE and
![]() $\rho _{y,\tilde y} $
differences were not relevant within each population. Given these small statistical differences, Model AM was expanded to Model E on the basis of Model AM4.
$\rho _{y,\tilde y} $
differences were not relevant within each population. Given these small statistical differences, Model AM was expanded to Model E on the basis of Model AM4.
Table 2.
χ
−2 hyperparameter specifications and model comparison statistics for the C57BL/6J strain under Models 0 and AM (a) and Models E (b). Goodness of fit was assessed by the deviance information criterion (DIC), whereas predictive ability was evaluated by the mean square error and the correlation coefficient between real and predicted data (
![]() $\rho _{y,\hat y} $
)
$\rho _{y,\hat y} $
)
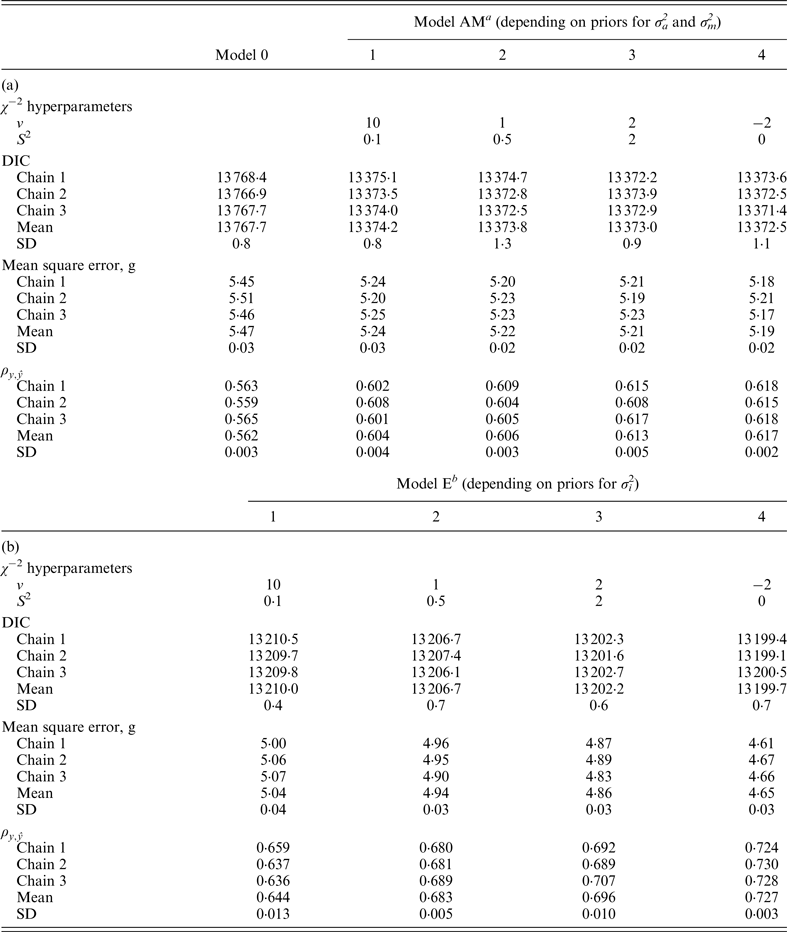
a Mixed linear model including founder-related and mutational genetic effects.
b Mixed linear model including founder-related, mutational and epistatic genetic effects.
SD: Standard deviation.
Table 3.
χ
−2 hyperparameter specifications and model comparison statistics for the C57BL/6Jhg/hg strain under Models 0 and AM (a) and Models E (b). Goodness of fit was assessed by the deviance information criterion (DIC), whereas predictive ability was evaluated by the mean square error and the correlation coefficient between real and predicted data (
![]() $\rho _{y,\hat y} $
)
$\rho _{y,\hat y} $
)
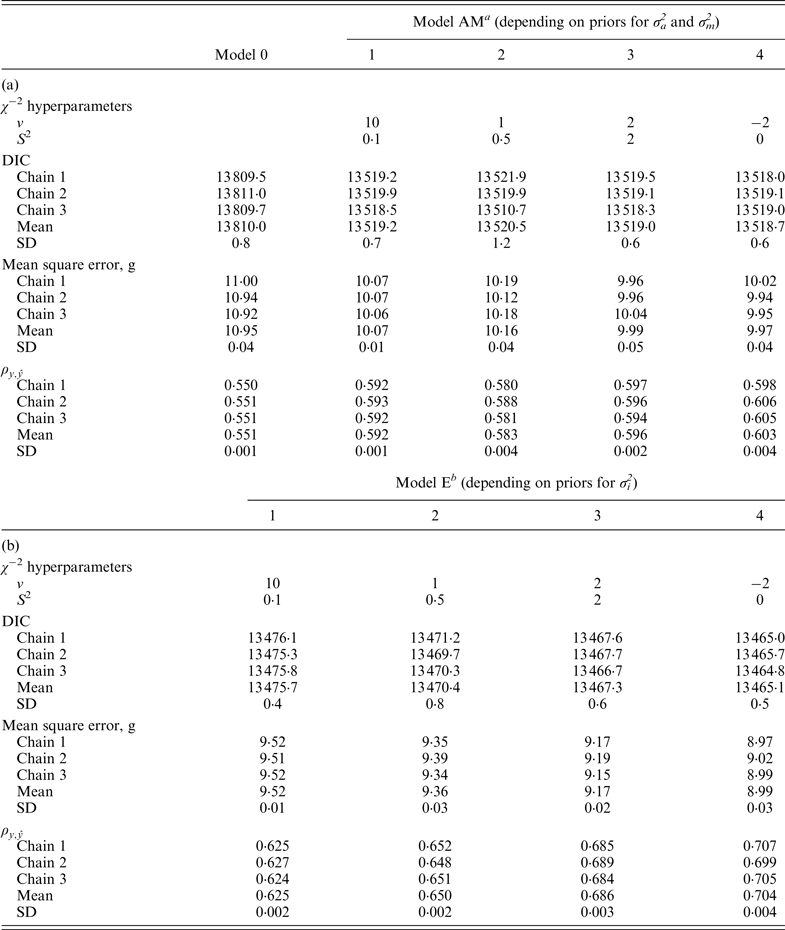
a Mixed linear model including founder-related and mutational genetic effects.
b Mixed linear model including founder-related, mutational and epistatic genetic effects.
Model performance under the four alternative a priori distributions for σ
i
2
provided very similar results on B6 and B6
hg/hg
data sets. DIC favored Model E4 (13 199·7 and 13 465·1, respectively) with slight and non-relevant advantages on Model E3 (13 202·2 and 13 467·3, respectively). The remaining parameterizations for σ
i
2
revealed larger than 5 DIC unit penalizations, discarding the restrictive scenarios drawn by these priors. Both MSE and
![]() $\rho _{y,\tilde y} $
showed a similar trend, corroborating the advantage of Model E3 and Model E4 in terms of predictive ability too. In conclusion, Model EPIPR4 reduced DIC units from Model AM4 by 172·8 (B6 population) and 53·6 (B6
hg/hg
population), providing decisive evidence about epistasis in our populations.
$\rho _{y,\tilde y} $
showed a similar trend, corroborating the advantage of Model E3 and Model E4 in terms of predictive ability too. In conclusion, Model EPIPR4 reduced DIC units from Model AM4 by 172·8 (B6 population) and 53·6 (B6
hg/hg
population), providing decisive evidence about epistasis in our populations.
(iii) Variance components
Variance components estimated under Model E3 and Model E4 showed minimal differences and highest posterior density regions at 95% (HPD95) were fully overlapped (results not shown). Variance components were reported on the basis of Model E4 (and Model AM4). Founder-related additive genetic variance was moderate in B6 and B6 hg/hg populations, accounting for the 6·8 and 6·0% of the phenotypic variance, respectively. Although modal estimates suggested a slight reduction from the values obtained under Model AM4 (9·2 and 8·2%, respectively), HPD95 were overlapped and discarded any significant departure. On the other hand, σ m 2 was small and represented ~1% of the phenotypic variance in both populations. The final target of our analyses, σ i 2 , was remarkably high in the B6 (0·505) and B6 hg/hg (1·192) data sets, with the HPD95 values far from the null estimate. The modal contribution of this variance component to the phenotypic variance was 9·5 and 11·3%, respectively; HPD95 started at values larger than 3% of the phenotypic variance, providing decisive evidence about the biological relevance of epistatic interactions on 9WK body weight in mice. Although a detailed pairwise comparison between the estimates from Model AM4 and Model E4 did not reveal relevant departures in addition to σ i 2 , a small reduction of the σ e 2 , could be suggested in terms of modal estimates. This value suggests that epistatic variability was mainly accumulated in the residual term of Model AM4, without discarding the partial absorption of epistatic effects in the remaining genetic and environmental variance components.
Modal estimates for correlation coefficients between each pairwise comparison of genetic effects (a, m and a × m) were low and positive, ranging from 0·182 (a vs. m; B6) to 0·342 (a vs. a × m; B6). Moreover, correlation coefficients between genetic effects and residual terms (e) were even smaller, the maximum modal estimate being 0·150 (m vs. e; B6 hg/hg ) and the minimum being slightly lower than zero (−0·022; a × m vs. e; B6). It is important to highlight that HPD95 were wide in all cases and included the null estimate by far; width of HPD95 took values between 0·331 and 0·543 correlation units.
4. Discussion
(i) Mouse strains and 9WK body weight
Although a description of raw phenotypes was not the principal aim of this research, phenotypic and pedigree data are the starting point for subsequent genetic analyses; their formal characterization provides essential information for an accurate interpretation of genetic estimates from complex mixed linear analyses. In a similar way, relevant information is contributed by the origin and genetic background inherent to each mouse strain involved in the experimental design. Both B6 and B6 hg/hg mice were closely related, since B6 hg/hg strain was originated by introgressing the hg mutation into the B6 background (Bradford & Famula, Reference Bradford and Famula1984). This mutation and a stretch of AKR/J sequence around the mutation (Horvat & Medrano, Reference Horvat and Medrano1996) were the known genetic differences between these two inbred strains. Nevertheless, B6 and B6 hg/hg strains were independently bred for more than 20 generations and new mutations arose separately and accumulated in each strain. On the basis of the results of Casellas & Medrano (Reference Casellas and Medrano2008) and Niu & Liang (Reference Niu and Liang2009), departures between B6 and B6 hg/hg strains could be by far greater than the anticipated hg mutation and AKR/J sequences.
All mice were kept in the same vivarium and under very similar husbandry practices; therefore, phenotypic differences must be mainly due to the loci determining 9WK body weight. B6 hg/hg mice were almost 10 g heavier at 9WK than their B6 mice, as expected due to the hg mutation (Bradford & Famula, Reference Bradford and Famula1984). In a similar way, phenotypic variance was also larger for B6 hg/hg mice (34·40 g2 vs. 9·34 g2), although this departure in dispersion parameters could not be anticipated by the allelic effect substitution of the hg mutation. Note that the inheritance pattern of this mutation was described as recessive with nearly complete penetrance (Bradford & Famula, Reference Bradford and Famula1984). Assuming a slight distortion on the B6 hg/hg phenotypic variance due to a residual departure from complete penetrance, the increasing phenotypic variability must be related to developmental instability (Vishalakshi & Singh, Reference Vishalakshi and Singh2008; Debat et al., Reference Debat, Debelle and Dworkin2009) and a scale effect, although the accumulation of new genetic variability by mutation cannot be completely discarded (Casellas & Medrano, Reference Casellas and Medrano2008). Indeed, epistatic QTL for growth and obesity were described between the hg mutation and several genomic locations in other chromosomes (Corva et al., Reference Corva, Horvat and Medrano2001). This analytical evidence suggested an increasing number of genomic targets sensitive to new mutations in the B6 hg/hg background; some new mutations modulating these genomic targets or other steps of the growth hormone/insulin-like growth factor 1 pathway could be responsible for part of this increased phenotypic variability. Given that our research focused on the partition of the phenotypic variance from different genetic and environmental sources, changes in phenotypic variance between our two related strains was of special interest.
(ii) Mixed linear models and a priori distributions
Making comparisons between models is a topic of major interest in statistical genetics given the substantial impact that a model can have on statistical inference. This phenomenon is of particular relevance in Bayesian analyses where both model structure and a priori information for model parameters could have a deep impact on final conclusions. Whereas experimental data themselves must not be influenced by arbitrary choices, prior distributions are arbitrarily chosen from previous knowledge of the parameters of interest. Given that studies on the epistatic ability of new mutations were not previously conducted, our a priori assumptions became a blind choice with unpredictable consequences on the posterior inference (Gianola & Fernando, Reference Gianola and Fernando1986; Blasco, Reference Blasco2001). Within this frame, our analyses examined model performance in two areas: (1) analysing the relevance of the epistatic interaction term between new mutations and founder-related effects and (2) studying the consistency of different a priori assumptions for the genetic variance components.
Assuming a mixed linear model without additive genetic effects as starting point, both B6 and B6
hg/hg
data sets showed a substantial reduction (increase) of the DIC and MSE (
![]() $\rho _{y,\tilde y} $
) statistics when a and m effects were included. Note that both populations were considered as fully inbred populations, although the presence of two different sources of additive genetic variance impaired the assumption of genetic homogeneity typically made on these inbred strains of mice (Festing, Reference Festing1979). These results agreed with the previous conclusions of Casellas & Medrano (Reference Casellas and Medrano2008), where a statistically significant and biologically relevant source of genetic variance was detected for litter size in an inbred population of B6 mice. The preliminary comparison of different a priori χ
–2
distributions for σ
a
2
and σ
m
2
did not reveal relevant departures in terms of DIC, MSE and
$\rho _{y,\tilde y} $
) statistics when a and m effects were included. Note that both populations were considered as fully inbred populations, although the presence of two different sources of additive genetic variance impaired the assumption of genetic homogeneity typically made on these inbred strains of mice (Festing, Reference Festing1979). These results agreed with the previous conclusions of Casellas & Medrano (Reference Casellas and Medrano2008), where a statistically significant and biologically relevant source of genetic variance was detected for litter size in an inbred population of B6 mice. The preliminary comparison of different a priori χ
–2
distributions for σ
a
2
and σ
m
2
did not reveal relevant departures in terms of DIC, MSE and
![]() $\rho _{y,\tilde y} $
. Although DIC discrepancies did not reach the 3–5 DIC units suggested by Spiegelhalter et al. (Reference Spiegelhalter, Best, Carlin and van der Linde2002, Reference Spiegelhalter, Thomas, Best and Lunn2003), flat a priori distributions for σ
a
2
and σ
m
2
were assumed for further analyses.
$\rho _{y,\tilde y} $
. Although DIC discrepancies did not reach the 3–5 DIC units suggested by Spiegelhalter et al. (Reference Spiegelhalter, Best, Carlin and van der Linde2002, Reference Spiegelhalter, Thomas, Best and Lunn2003), flat a priori distributions for σ
a
2
and σ
m
2
were assumed for further analyses.
The inclusion of the a × m was also favoured in both data sets (Tables 2 and 3). In this case, the different a priori distributions provided some relevant differences in both data sets, reducing the DIC and MSE estimates and increasing the
![]() $\rho _{y,\tilde y} $
estimate with smoothed χ
–2
distribution. As for σ
a
2
and σ
m
2
, Model E4 reached the best performance, although differences with Model E3 were not statistically significant in both data sets. In any case, the small departures observed between the different a priori distributions for σ
i
2
suggested that the experimental data had enough information content to override moderate influences of prior information, even under very extreme assumptions. As previously reported by Casellas & Medrano (Reference Casellas and Medrano2008), these models including mutational terms seemed to perform better under a vague assumption for genetic variance components over the parameter space.
$\rho _{y,\tilde y} $
estimate with smoothed χ
–2
distribution. As for σ
a
2
and σ
m
2
, Model E4 reached the best performance, although differences with Model E3 were not statistically significant in both data sets. In any case, the small departures observed between the different a priori distributions for σ
i
2
suggested that the experimental data had enough information content to override moderate influences of prior information, even under very extreme assumptions. As previously reported by Casellas & Medrano (Reference Casellas and Medrano2008), these models including mutational terms seemed to perform better under a vague assumption for genetic variance components over the parameter space.
(iii) Genetic variability in inbred mouse strains
Genetic variances were discussed on the basis of Model E4 (and Model AM4) because it reached the smallest DIC and MSE estimates and the largest
![]() $\rho _{y,\tilde y} $
estimate, and the differences between estimated variance components across a priori distributions for genetic variances were minimal (results not shown). In B6 and B6
hg/hg
mice 9WK body weight was moderately heritable, with σ
a
2
accounting for 6·8 and 6·0% of the phenotypic variance, respectively. Our estimates were far from the heritability values obtained in other outbred populations such as beef cattle, i.e., 0·25 (Frizzas et al., Reference Frizzas, Grossi, Buzanskas, Paz, Bezerra, Lôbo, Oliveira and Munari2009), dairy cattle, i.e., 0·48–0·57 (Toshniwal et al., Reference Toshniwal, Dechow, Cassell, Appuhamy and Varga2008), goats, i.e., 0·35–0·47 (Snyman & Olivier Reference Snyman and Olivier1999), and mice, i.e., 0·56 (Leamy et al., Reference Leamy, Elo, Nielsen, Van Vleck and Pomp2005), although they revealed a high degree of genetic variability for an inbred population. These estimates were accompanied by relevant mutational variances accounting for ~1% of the phenotypic variance (Table 4). Note that estimated mutational heritabilities were close to the upper limit of the values reviewed by Lynch (Reference Lynch1988) and Houle et al. (Reference Houle, Morikawa and Lynch1996), and agreed with mutational heritabilities reported by Caballero et al. (Reference Caballero, Keightley and Hill1995) in other B6-related mouse strains. As was previously suggested by Casellas & Medrano (Reference Casellas and Medrano2008) in the same B6 population, σ
m
2
must be viewed in highly inbred strains as a lower limit for the infinitesimal polygenic genetic variance, although higher σ
a
2
estimates can be anticipated depending on the stationary equilibrium reached by mutation and genetic drift phenomena. Given the full-sib mating system applied in our populations, a quick depletion of additive genetic variance could be anticipated and thus, σ
a
2
must originate from short-term mutations arising in the few previous generations, these being characterized by σ
m
2
(Casellas & Medrano, Reference Casellas and Medrano2008). Additional genetic mechanisms contributing a low level of genetic variance cannot be discarded, e.g., loci under balancing selection (Crow, Reference Crow2010), although the relevance of σ
m
2
in our experimental populations is of no doubt (Table 4). In any case, this remarkable amount of founder-related and mutational additive genetic variability provided an excellent frame for the study of genetic epistasis between both additive genetic variance components. It is important to highlight that residuals and a, m and a × m effects were moderately correlated, although the posterior distribution of these correlation coefficients included the null estimate within the HPD95 in all cases. Nevertheless, a certain degree of collinearity between these genetic and residual sources of variation cannot be completely discarded under the current analytical model, this partially impairing the accuracy of final estimates. This could be anticipated by the original developments of Wray (Reference Wray1990) and relies on the fact that breeding values are linear functions of mutation effects (Wray, Reference Wray1990) and part of the epistatic effect could be absorbed by founder-related additive genetic effects (Cheverud & Routman, Reference Cheverud and Routman1995; Hill et al., Reference Hill, Goddard and Visscher2008; Crow, Reference Crow2010).
$\rho _{y,\tilde y} $
estimate, and the differences between estimated variance components across a priori distributions for genetic variances were minimal (results not shown). In B6 and B6
hg/hg
mice 9WK body weight was moderately heritable, with σ
a
2
accounting for 6·8 and 6·0% of the phenotypic variance, respectively. Our estimates were far from the heritability values obtained in other outbred populations such as beef cattle, i.e., 0·25 (Frizzas et al., Reference Frizzas, Grossi, Buzanskas, Paz, Bezerra, Lôbo, Oliveira and Munari2009), dairy cattle, i.e., 0·48–0·57 (Toshniwal et al., Reference Toshniwal, Dechow, Cassell, Appuhamy and Varga2008), goats, i.e., 0·35–0·47 (Snyman & Olivier Reference Snyman and Olivier1999), and mice, i.e., 0·56 (Leamy et al., Reference Leamy, Elo, Nielsen, Van Vleck and Pomp2005), although they revealed a high degree of genetic variability for an inbred population. These estimates were accompanied by relevant mutational variances accounting for ~1% of the phenotypic variance (Table 4). Note that estimated mutational heritabilities were close to the upper limit of the values reviewed by Lynch (Reference Lynch1988) and Houle et al. (Reference Houle, Morikawa and Lynch1996), and agreed with mutational heritabilities reported by Caballero et al. (Reference Caballero, Keightley and Hill1995) in other B6-related mouse strains. As was previously suggested by Casellas & Medrano (Reference Casellas and Medrano2008) in the same B6 population, σ
m
2
must be viewed in highly inbred strains as a lower limit for the infinitesimal polygenic genetic variance, although higher σ
a
2
estimates can be anticipated depending on the stationary equilibrium reached by mutation and genetic drift phenomena. Given the full-sib mating system applied in our populations, a quick depletion of additive genetic variance could be anticipated and thus, σ
a
2
must originate from short-term mutations arising in the few previous generations, these being characterized by σ
m
2
(Casellas & Medrano, Reference Casellas and Medrano2008). Additional genetic mechanisms contributing a low level of genetic variance cannot be discarded, e.g., loci under balancing selection (Crow, Reference Crow2010), although the relevance of σ
m
2
in our experimental populations is of no doubt (Table 4). In any case, this remarkable amount of founder-related and mutational additive genetic variability provided an excellent frame for the study of genetic epistasis between both additive genetic variance components. It is important to highlight that residuals and a, m and a × m effects were moderately correlated, although the posterior distribution of these correlation coefficients included the null estimate within the HPD95 in all cases. Nevertheless, a certain degree of collinearity between these genetic and residual sources of variation cannot be completely discarded under the current analytical model, this partially impairing the accuracy of final estimates. This could be anticipated by the original developments of Wray (Reference Wray1990) and relies on the fact that breeding values are linear functions of mutation effects (Wray, Reference Wray1990) and part of the epistatic effect could be absorbed by founder-related additive genetic effects (Cheverud & Routman, Reference Cheverud and Routman1995; Hill et al., Reference Hill, Goddard and Visscher2008; Crow, Reference Crow2010).
Table 4. Modal estimates and highest posterior density region at 95% (HPD95) for the variance components and heritabilities for the C57BL/6J (a) and C57BL/6Jhg/hg (b) data set
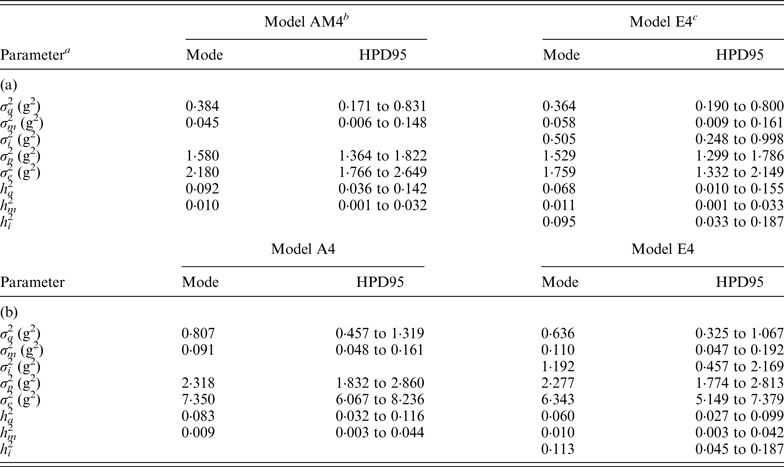
a σ a 2: founder-related additive genetic variance; σ m 2: mutational variance; σ i 2: epistatic variance; σ p 2: permanent environmental variance; σ e 2: residual variance; h a 2: founder-related additive heritability; h m 2: mutational heritability; h i 2: epistatic heritability.
b Mixed linear model including founder-related and mutational genetic effects. Genetic variances were modeled under flat a priori distributions within a Bayesian context.
c Mixed linear model including founder-related, mutational and epistatic genetic effects. Genetic variances were modeled under flat a priori distributions within a Bayesian context.
Epistasis, the effect due to the interaction between different genes, has been reported in F2 crosses from inbred mouse strains (Caron et al., Reference Caron, Loredo-Osti, Morgan and Malo2005; Yi et al., Reference Yi, Zinniel, Kim, Eisen, Bartolucci, Allison and Pomp2006; Leamy et al., Reference Leamy, Pomp and Lightfoot2008) as well as livestock (Barendse et al., Reference Barendse, Harrison, Hawken, Ferguson, Thompson, Thomas and Bunch2007; Noguera et al., Reference Noguera, Rodríguez, Varona, Tomás, Muñoz, Ramírez, Barragán, Arqué, Bidanel, Amills, Óvilo and Sánchez2009; Uemoto et al., Reference Uemoto, Sato, Ohnishi, Terai, Komatsuda and Kobayashi2009) and crop species (Silva & Hallauer, Reference Silva and Hallauer1975; Goldringer et al., Reference Goldringer, Brabant and Gallais1997; Xu & Jia, Reference Xu and Jia2007). In these studies, epistasis was modelled on a QTL basis (Leamy et al., Reference Leamy, Pomp and Lightfoot2008; Noguera et al., Reference Noguera, Rodríguez, Varona, Tomás, Muñoz, Ramírez, Barragán, Arqué, Bidanel, Amills, Óvilo and Sánchez2009) or as an additional variance component (Caron et al., Reference Caron, Loredo-Osti, Morgan and Malo2005; Yi et al., Reference Yi, Zinniel, Kim, Eisen, Bartolucci, Allison and Pomp2006). All designs assumed that the epistatic load inherent to each experimental population did not vary during data collection, even when this process spanned several generations. This broad assumption was far from being realistic although it provided the first confirmations on the relevance of epistasis in the genome of several species. Our research was an endeavour to generalize the study of epistasis when new mutations were also accounted for in the analysis and it represents the first experimental evidence for this kind of mutational contribution in the scientific literature (Table 4).
Despite its basic role in evolution and speciation (Cheverud & Routman, Reference Cheverud and Routman1995), the link between epistasis and mutation is controversial. Our results showed that this link exists without doubt in laboratory mice and accounts for a remarkable percentage of the total phenotypic variance (~10%; Table 4), even larger than the direct contribution of new mutations. Although not more than a hypothesis, this advantage for σ i 2 when comparing with σ m 2 could be related to the possibility of multiple epistatic interactions originating from a unique mutation (i.e., larger variability for σ i 2 ), whereas the mutation itself does not contribute more than its direct effect on σ m 2 . Taking Wray (Reference Wray1990) as a starting point, new mutations not only contributed direct effects on 9WK body weight in mice but also interacted with pre-existing polymorphisms in the mouse genome. Note that our analyses focused on a short period of time (i.e., five or six generations) where, even under full-sib mating, σ a 2 was not depleted and allowed for a proper estimation of the interaction term. Nevertheless, these results from inbred mice strains cannot be directly generalized to livestock species where much of the recent additive genetic variance is the result of past and recent selection (Nagylaki, Reference Nagylaki1993; Crow, Reference Crow2010), and a smaller σ i 2 must be anticipated. However, these results provide new evidence about the relevant role of new mutations on maintaining genetic variability in mammals and must be viewed as an important component affecting the genetic fragility of inbred populations of laboratory species. Although previous authors have suggested that inbred strains cannot be considered as genetically homogeneous (Taft et al., Reference Taft, Davisson and Wiles2006; Stevens et al., Reference Stevens, Banks, Festing and Fisher2007; Casellas & Medrano, Reference Casellas and Medrano2008), the additional contribution of epistatic mutational effects rules out any doubts on the genetic instability of inbred mice, maybe even in some cases impairing reproducibility of research experiments.
The authors are indebted to James F. Crow (University of Wisconsin, Madison, WI) for his helpful comments on this manuscript.
5. Financial support
This work was partially supported by NIH grant DK69978. The research contract of J. Casellas was partially financed by Spain's Ministerio de Ciencia e Innovación (program Ramón y Cajal).
6. Declaration of interest
None.







