Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Chekhov, Leonid Olegovich
2020.
Координаты Фенхеля-Нильсена и скобки Голдмана.
Успехи математических наук,
Vol. 75,
Issue. 5(455),
p.
153.
Chekhov, L. O.
2020.
Fenchel–Nielsen coordinates and Goldman brackets.
Russian Mathematical Surveys,
Vol. 75,
Issue. 5,
p.
929.
McConville, Thomas
Sagan, Bruce E.
and
Smyth, Clifford
2021.
On a rank-unimodality conjecture of Morier-Genoud and Ovsienko.
Discrete Mathematics,
Vol. 344,
Issue. 8,
p.
112483.
Morier-Genoud, Sophie
and
Ovsienko, Valentin
2021.
Quantum Numbers and q-Deformed Conway–Coxeter Friezes.
The Mathematical Intelligencer,
Vol. 43,
Issue. 2,
p.
61.
Ren, Xin
2022.
On radiuses of convergence of q-metallic numbers and related q-rational numbers.
Research in Number Theory,
Vol. 8,
Issue. 3,
Schiffler, Ralf
and
Whiting, David
2022.
Tilting modules arising from knot invariants.
Journal of Pure and Applied Algebra,
Vol. 226,
Issue. 9,
p.
107041.
Souza, Carlos E. C.
Moreno, Davi
Figueiredo, Ravi B. D.
Chaves, Daniel P. B.
and
Pimentel, Cecilio
2023.
q-Analogs Over Finite Fields: Definition, Algebraic Properties, and Application in Pseudo-Random Number Generators.
IEEE Transactions on Circuits and Systems II: Express Briefs,
Vol. 70,
Issue. 8,
p.
3064.
Elizalde, Sergi
and
Sagan, Bruce E.
2023.
Partial Rank Symmetry of Distributive Lattices for Fences.
Annals of Combinatorics,
Vol. 27,
Issue. 2,
p.
433.
Bostan, Alin
and
Yurkevich, Sergey
2023.
Fast computation of the N-th term of a q-holonomic sequence and applications.
Journal of Symbolic Computation,
Vol. 115,
Issue. ,
p.
96.
Kantarcı Oğuz, Ezgi
and
Ravichandran, Mohan
2023.
Rank polynomials of fence posets are unimodal.
Discrete Mathematics,
Vol. 346,
Issue. 2,
p.
113218.
Elizalde, Sergi
Plante, Matthew
Roby, Tom
and
Sagan, Bruce E.
2023.
Rowmotion on fences.
Algebraic Combinatorics,
Vol. 6,
Issue. 1,
p.
17.
Bapat, Asilata
Becker, Louis
and
Licata, Anthony M.
2023.
q-deformed rational numbers and the 2-Calabi–Yau category of type .
Forum of Mathematics, Sigma,
Vol. 11,
Issue. ,
Sikora, Adam S.
2023.
Tangle equations, the Jones conjecture, slopes of surfaces in tangle complements, and q-deformed rationals.
Canadian Journal of Mathematics,
p.
1.
Morier-Genoud, Sophie
Ovsienko, Valentin
and
Veselov, Alexander P
2024.
Burau Representation of Braid Groups and q-Rationals.
International Mathematics Research Notices,
Chung, Won Sang
Dong, Shi-Hai
and
Hassanabadi, Hassan
2024.
The q-deformed Schrödinger equation based on the q-map: one dimensional case.
The European Physical Journal Plus,
Vol. 139,
Issue. 3,
Kantarcı Oǧuz, Ezgi
Özel, Cem Yalım
and
Ravichandran, Mohan
2024.
Chainlink Polytopes and Ehrhart Equivalence.
Annals of Combinatorics,
Labbé, Sébastien
Lapointe, Mélodie
and
Steiner, Wolfgang
2024.
A q-analog of the Markoff injectivity conjecture holds.
Algebraic Combinatorics,
Vol. 6,
Issue. 6,
p.
1677.
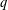 $q$-DEFORMED RATIONALS AND
$q$-DEFORMED RATIONALS AND 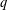 $q$-CONTINUED FRACTIONS
$q$-CONTINUED FRACTIONS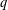 $q$-deformed rational numbers and
$q$-deformed rational numbers and 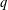 $q$-deformed continued fractions. A
$q$-deformed continued fractions. A 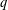 $q$-deformed rational is encoded by a triangulation of a polygon and can be computed recursively. The recursive formula is analogous to the
$q$-deformed rational is encoded by a triangulation of a polygon and can be computed recursively. The recursive formula is analogous to the 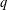 $q$-deformed Pascal identity for the Gaussian binomial coefficients, but the Pascal triangle is replaced by the Farey graph. The coefficients of the polynomials defining the
$q$-deformed Pascal identity for the Gaussian binomial coefficients, but the Pascal triangle is replaced by the Farey graph. The coefficients of the polynomials defining the 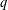 $q$-rational count quiver subrepresentations of the maximal indecomposable representation of the graph dual to the triangulation. Several other properties, such as total positivity properties,
$q$-rational count quiver subrepresentations of the maximal indecomposable representation of the graph dual to the triangulation. Several other properties, such as total positivity properties, 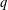 $q$-deformation of the Farey graph, matrix presentations and
$q$-deformation of the Farey graph, matrix presentations and 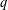 $q$-continuants are given, as well as a relation to the Jones polynomial of rational knots.
$q$-continuants are given, as well as a relation to the Jones polynomial of rational knots.



