Hostname: page-component-7479d7b7d-m9pkr Total loading time: 0 Render date: 2024-07-09T06:28:25.001Z Has data issue: false hasContentIssue false
  • English
  • Français

THE INTEGRAL COHOMOLOGY OF THE HILBERT SCHEME OF TWO POINTS

Part of: Cycles and subschemes Fiber spaces and bundles

Published online by Cambridge University Press:  27 April 2016

BURT TOTARO
BURT TOTARO*
Affiliation:
UCLA Mathematics Department, Box 951555, Los Angeles, CA 90095-1555, USA; totaro@math.ucla.edu

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The Hilbert scheme 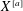$X^{[a]}$ of points on a complex manifold 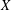$X$ is a compactification of the configuration space of $a$-element subsets of 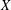$X$. The integral cohomology of 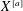$X^{[a]}$ is more subtle than the rational cohomology. In this paper, we compute the mod 2 cohomology of 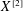$X^{[2]}$ for any complex manifold 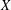$X$, and the integral cohomology of 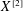$X^{[2]}$ when 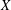$X$ has torsion-free cohomology.

MSC classification

Primary: 14C05: Parametrization (Chow and Hilbert schemes)
Secondary: 55R80: Discriminantal varieties, configuration spaces
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 4 , 2016 , e8
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author 2016

References

Bödigheimer, C.-F., Cohen, F. and Taylor, L., ‘On the homology of configuration spaces’, Topology 28 (1989), 111–123.Google Scholar
Bott, R. and Tu, L., Differential Forms in Algebraic Topology, (Springer, New York–Berlin, 1982).Google Scholar
Cheah, J., ‘Cellular decompositions for nested Hilbert schemes of points’, Pacific J. Math. 183 (1998), 39–90.Google Scholar
Clemens, C. H. and Griffiths, P. A., ‘The intermediate Jacobian of the cubic threefold’, Ann. of Math. (2) 95 (1972), 281–356.Google Scholar
Colliot-Thélène, J.-L. and Pirutka, A., ‘Hypersurfaces quartiques de dimension 3: non rationalité stable’, Ann. Sci. Éc. Norm. Supér. 49 (2016), 373–399.Google Scholar
Dold, A., ‘Decomposition theorems for S (n)-complexes’, Ann. of Math. (2) 75 (1962), 8–16.Google Scholar
Friedman, R. and Morgan, J., Smooth Four-Manifolds and Complex Surfaces, (Springer, Berlin, 1994).Google Scholar
Fulton, W., Intersection Theory, (Springer, Berlin, 1998).Google Scholar
Hatcher, A., Algebraic Topology, (Cambridge University Press, Cambridge, 2002).Google Scholar
Markman, E., ‘Integral generators for the cohomology ring of moduli spaces of sheaves over Poisson surfaces’, Adv. Math. 208 (2007), 622–646.CrossRefGoogle Scholar
May, J. P., A Concise Course in Algebraic Topology, (University of Chicago Press, Chicago, 1999).Google Scholar
McCleary, J., A User’s Guide to Spectral Sequences, (Cambridge University Press, Cambridge, 2001).Google Scholar
Milgram, R. J., ‘The homology of symmetric products’, Trans. Amer. Math. Soc. 138 (1969), 251–265.CrossRefGoogle Scholar
Milgram, R. J. and Löffler, P., ‘The structure of deleted symmetric products’, Braids (Santa Cruz, 1986) , 415–424. (American Mathematical Society, Providence, 1988).Google Scholar
Milnor, J. and Stasheff, J., Characteristic Classes, (Princeton University Press, Princeton, 1974).Google Scholar
Shen, M. and Vial, C., ‘The motive of the Hilbert cube $X^{[3]}$ ’, Preprint, 2015,arXiv:1503.00876.Google Scholar
Thom, R., ‘Variétés plongées et i-carrés’, C. R. Acad. Sci. Paris 230 (1950), 507–508.Google Scholar
Thom, R., ‘Quelques propriétés globales des variétés différentiables’, Comment. Math. Helv. 28 (1954), 17–86.Google Scholar
Totaro, B., ‘Hypersurfaces that are not stably rational’, J. Amer. Math. Soc., doi:10.1090/jams/840.Google Scholar
Voisin, C., Hodge Theory and Complex Algebraic Geometry, vol. 1. (Cambridge University Press, Cambridge, 2002).Google Scholar
Voisin, C., ‘Unirational threefolds with no universal codimension 2 cycle’, Invent. Math. 201 (2015), 207–237.Google Scholar
Voisin, C., ‘On the universal CH 0 group of cubic hypersurfaces’, J. Eur. Math. Soc., to appear.Google Scholar