No CrossRef data available.
Article contents
GLOBAL ACTIONS AND VECTOR 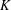 $K$-THEORY
$K$-THEORY
Published online by Cambridge University Press: 15 January 2020
Abstract
Purely algebraic objects like abstract groups, coset spaces, and G-modules do not have a notion of hole as do analytical and topological objects. However, equipping an algebraic object with a global action reveals holes in it and thanks to the homotopy theory of global actions, the holes can be described and quantified much as they are in the homotopy theory of topological spaces. Part I of this article, due to the first author, starts by recalling the notion of a global action and describes in detail the global actions attached to the general linear, elementary, and Steinberg groups. With these examples in mind, we describe the elementary homotopy theory of arbitrary global actions, construct their homotopy groups, and revisit their covering theory. We then equip the set 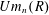 $Um_{n}(R)$ of all unimodular row vectors of length
$Um_{n}(R)$ of all unimodular row vectors of length  $n$ over a ring
$n$ over a ring 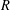 $R$ with a global action. Its homotopy groups
$R$ with a global action. Its homotopy groups 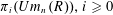 $\unicode[STIX]{x1D70B}_{i}(Um_{n}(R)),i\geqslant 0$ are christened the vector
$\unicode[STIX]{x1D70B}_{i}(Um_{n}(R)),i\geqslant 0$ are christened the vector 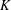 $K$-theory groups
$K$-theory groups 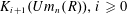 $K_{i+1}(Um_{n}(R)),i\geqslant 0$ of
$K_{i+1}(Um_{n}(R)),i\geqslant 0$ of 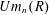 $Um_{n}(R)$. It is known that the homotopy groups
$Um_{n}(R)$. It is known that the homotopy groups 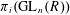 $\unicode[STIX]{x1D70B}_{i}(\text{GL}_{n}(R))$ of the general linear group
$\unicode[STIX]{x1D70B}_{i}(\text{GL}_{n}(R))$ of the general linear group 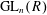 $\text{GL}_{n}(R)$ viewed as a global action are the Volodin
$\text{GL}_{n}(R)$ viewed as a global action are the Volodin 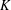 $K$-theory groups
$K$-theory groups 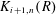 $K_{i+1,n}(R)$. The main result of Part I is an algebraic construction of the simply connected covering map
$K_{i+1,n}(R)$. The main result of Part I is an algebraic construction of the simply connected covering map 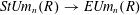 $\mathit{StUm}_{n}(R)\rightarrow \mathit{EUm}_{n}(R)$ where
$\mathit{StUm}_{n}(R)\rightarrow \mathit{EUm}_{n}(R)$ where 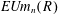 $\mathit{EUm}_{n}(R)$ is the path connected component of the vector
$\mathit{EUm}_{n}(R)$ is the path connected component of the vector 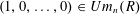 $(1,0,\ldots ,0)\in Um_{n}(R)$. The result constructs the map as a specific quotient of the simply connected covering map
$(1,0,\ldots ,0)\in Um_{n}(R)$. The result constructs the map as a specific quotient of the simply connected covering map 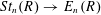 $St_{n}(R)\rightarrow E_{n}(R)$ of the elementary global action
$St_{n}(R)\rightarrow E_{n}(R)$ of the elementary global action 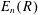 $E_{n}(R)$ by the Steinberg global action
$E_{n}(R)$ by the Steinberg global action 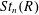 $St_{n}(R)$. As expected,
$St_{n}(R)$. As expected, 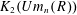 $K_{2}(Um_{n}(R))$ is identified with
$K_{2}(Um_{n}(R))$ is identified with 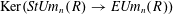 $\text{Ker}(\mathit{StUm}_{n}(R)\rightarrow \mathit{EUm}_{n}(R))$. Part II of the paper provides an exact sequence relating stability for the Volodin
$\text{Ker}(\mathit{StUm}_{n}(R)\rightarrow \mathit{EUm}_{n}(R))$. Part II of the paper provides an exact sequence relating stability for the Volodin 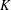 $K$-theory groups
$K$-theory groups 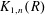 $K_{1,n}(R)$ and
$K_{1,n}(R)$ and 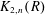 $K_{2,n}(R)$ to vector
$K_{2,n}(R)$ to vector 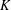 $K$-theory groups.
$K$-theory groups.
- Type
- Algebra
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author(s) 2020




