Hostname: page-component-76fb5796d-2lccl Total loading time: 0 Render date: 2024-04-25T16:23:00.687Z Has data issue: false hasContentIssue false
  • English
  • Français

DNR AND INCOMPARABLE TURING DEGREES

Part of: Computability and recursion theory General logic

Published online by Cambridge University Press:  06 April 2016

MINZHONG CAI ,
NOAM GREENBERG  and
MICHAEL MCINERNEY
MINZHONG CAI
Affiliation:
Department of Mathematics, Dartmouth College, Hanover, NH 03755, USA
NOAM GREENBERG
Affiliation:
School of Mathematics Statistics and Operations Research, Victoria University of Wellington, P.O. Box 600, Wellington, New Zealand
MICHAEL MCINERNEY
Affiliation:
School of Mathematics Statistics and Operations Research, Victoria University of Wellington, P.O. Box 600, Wellington, New Zealand

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We construct an increasing 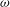${\it\omega}$-sequence 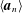$\langle \boldsymbol{a}_{n}\rangle$ of Turing degrees which forms an initial segment of the Turing degrees, and such that each 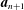$\boldsymbol{a}_{n+1}$ is diagonally nonrecursive relative to 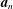$\boldsymbol{a}_{n}$. It follows that the DNR principle of reverse mathematics does not imply the existence of Turing incomparable degrees.

MSC classification

Primary: 03B30: Foundations of classical theories (including reverse mathematics)
Secondary: 03D28: Other Turing degree structures
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 4 , 2016 , e7
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2016

References

Ambos-Spies, K., Kjos-Hanssen, B., Lempp, S. and Slaman, T. A., ‘Comparing DNR and WWKL’, J. Symbolic Logic 69(4) (2004), 1089–1104.Google Scholar
Cai, M., ‘A 2-minimal non-GL2 degree’, J. Math. Log. 10(1–2) (2010), 1–30.Google Scholar
Cai, M., ‘A hyperimmune minimal degree and an ANR 2-minimal degree’, Notre Dame J. Form. Log. 51(4) (2010), 443–455.Google Scholar
Cai, M., ‘Elements of classical recursion theory: degree-theoretic properties and combinatorial properties’, PhD thesis, Cornell University, 2011.Google Scholar
Cai, M., ‘2-minimality, jump classes and a note on natural definability’, Ann. Pure Appl. Logic 165(2) (2014), 724–741.Google Scholar
Conidis, C. J., ‘A measure-theoretic proof of Turing incomparability’, Ann. Pure Appl. Logic 162(1) (2010), 83–88.Google Scholar
Greenberg, N. and Miller, J. S., ‘Diagonally non-recursive functions and effective Hausdorff dimension’, Bull. Lond. Math. Soc. 43(4) (2011), 636–654.Google Scholar
Jockusch, C. G. Jr, ‘Degrees of functions with no fixed points’, inLogic, Methodology and Philosophy of Science, VIII (Moscow, 1987), Studies in Logic and the Foundations of Mathematics, 126 (North-Holland, Amsterdam, 1989), 191–201.Google Scholar
Khan, M. and Miller, J. S., Forcing with bushy trees (in preparation).Google Scholar
Kučera, A. and Slaman, T. A., ‘Turing incomparability in Scott sets’, Proc. Amer. Math. Soc. 135(11) (2007), 3723–3731.CrossRefGoogle Scholar
Kumabe, M. and Lewis, A. E. M., ‘A fixed-point-free minimal degree’, J. Lond. Math. Soc. (2) 80(3) (2009), 785–797.Google Scholar
Lerman, M., ‘Degrees of unsolvability’, inPerspectives in Mathematical Logic (Springer, Berlin, 1983), Local and global theory.Google Scholar