Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Diamantis, Nikolaos
and
Drewitt, Joshua
2020.
Period functions associated to real-analytic modular forms.
Research in the Mathematical Sciences,
Vol. 7,
Issue. 3,
Broedel, Johannes
Kaderli, André
and
Schlotterer, Oliver
2020.
Two dialects for KZB equations: generating one-loop open-string integrals.
Journal of High Energy Physics,
Vol. 2020,
Issue. 12,
Edison, Alex
Guillen, Max
Johansson, Henrik
Schlotterer, Oliver
and
Teng, Fei
2021.
One-loop matrix elements of effective superstring interactions: α′-expanding loop integrands.
Journal of High Energy Physics,
Vol. 2021,
Issue. 12,
Britto, Ruth
Mizera, Sebastian
Rodriguez, Carlos
and
Schlotterer, Oliver
2021.
Coaction and double-copy properties of configuration-space integrals at genus zero.
Journal of High Energy Physics,
Vol. 2021,
Issue. 5,
Gerken, Jan E
Kleinschmidt, Axel
Mafra, Carlos R
Schlotterer, Oliver
and
Verbeek, Bram
2022.
Towards closed strings as single-valued open strings at genus one.
Journal of Physics A: Mathematical and Theoretical,
Vol. 55,
Issue. 2,
p.
025401.
Dorigoni, Daniele
Kleinschmidt, Axel
and
Treilis, Rudolfs
2022.
To the cusp and back: resurgent analysis for modular graph functions.
Journal of High Energy Physics,
Vol. 2022,
Issue. 11,
Dorigoni, Daniele
Green, Michael B
and
Wen, Congkao
2022.
The SAGEX review on scattering amplitudes Chapter 10: Selected topics on modular covariance of type IIB string amplitudes and their
N=4
supersymmetric Yang–Mills duals.
Journal of Physics A: Mathematical and Theoretical,
Vol. 55,
Issue. 44,
p.
443011.
Dorigoni, Daniele
Kleinschmidt, Axel
and
Schlotterer, Oliver
2022.
Poincaré series for modular graph forms at depth two. Part I. Seeds and Laplace systems.
Journal of High Energy Physics,
Vol. 2022,
Issue. 1,
Drewitt, Joshua
2022.
Laplace-eigenvalue equations for length three modular iterated integrals.
Journal of Number Theory,
Vol. 239,
Issue. ,
p.
78.
Diamantis, Nikolaos
2022.
Modular iterated integrals associated with cusp forms.
Forum Mathematicum,
Vol. 34,
Issue. 1,
p.
157.
Dorigoni, Daniele
Doroudiani, Mehregan
Drewitt, Joshua
Hidding, Martijn
Kleinschmidt, Axel
Matthes, Nils
Schlotterer, Oliver
and
Verbeek, Bram
2022.
Modular graph forms from equivariant iterated Eisenstein integrals.
Journal of High Energy Physics,
Vol. 2022,
Issue. 12,
Dorigoni, Daniele
Kleinschmidt, Axel
and
Schlotterer, Oliver
2022.
Poincaré series for modular graph forms at depth two. Part II. Iterated integrals of cusp forms.
Journal of High Energy Physics,
Vol. 2022,
Issue. 1,
Dorigoni, Daniele
and
Treilis, Rudolfs
2023.
Two string theory flavours of generalised Eisenstein series.
Journal of High Energy Physics,
Vol. 2023,
Issue. 11,
Magnusson, Tobias
and
Raum, Martin
2023.
Scalar‐valued depth two Eichler–Shimura integrals of cusp forms.
Transactions of the London Mathematical Society,
Vol. 10,
Issue. 1,
p.
156.
Mafra, Carlos R.
and
Schlotterer, Oliver
2023.
Tree-level amplitudes from the pure spinor superstring.
Physics Reports,
Vol. 1020,
Issue. ,
p.
1.
Rodriguez, Carlos
Schlotterer, Oliver
and
Zhang, Yong
2024.
Basis decompositions of genus-one string integrals.
Journal of High Energy Physics,
Vol. 2024,
Issue. 5,
Zhang, Yong
2024.
Advanced tools for basis decompositions of genus-one string integrals.
Journal of High Energy Physics,
Vol. 2024,
Issue. 5,
Frost, Hadleigh
Hidding, Martijn
Kamlesh, Deepak
Rodriguez, Carlos
Schlotterer, Oliver
and
Verbeek, Bram
2024.
Motivic coaction and single-valued map of polylogarithms from zeta generators.
Journal of Physics A: Mathematical and Theoretical,
Vol. 57,
Issue. 31,
p.
31LT01.
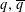 $q,\overline{q}$ and
$q,\overline{q}$ and 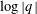 $\log |q|$ involving only rational numbers and single-valued multiple zeta values. The first nontrivial functions in this class are real-analytic Eisenstein series.
$\log |q|$ involving only rational numbers and single-valued multiple zeta values. The first nontrivial functions in this class are real-analytic Eisenstein series.

