Hostname: page-component-76fb5796d-vfjqv Total loading time: 0 Render date: 2024-04-25T20:41:06.824Z Has data issue: false hasContentIssue false
  • English
  • Français

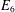$E_{6}$ AND THE ARITHMETIC OF A FAMILY OF NON-HYPERELLIPTIC CURVES OF GENUS 3

Part of: Arithmetic problems. Diophantine geometry Algebraic groups

Published online by Cambridge University Press:  12 January 2015

JACK A. THORNE
JACK A. THORNE*
Affiliation:
DPMMS, Wilberforce Road, Cambridge CB3 0WB, UK; thorne@dpmms.cam.ac.uk

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the arithmetic of a family of non-hyperelliptic curves of genus 3 over the field 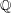$\mathbb{Q}$ of rational numbers. These curves are the nearby fibers of the semi-universal deformation of a simple singularity of type 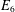$E_{6}$. We show that average size of the 2-Selmer sets of these curves is finite (if it exists). We use this to show that a positive proposition of these curves (when ordered by height) has integral points everywhere locally, but no integral points globally.

MSC classification

Primary: 14G05: Rational points
Secondary: 14L30: Group actions on varieties or schemes (quotients)
Type
Research Article
Information
Forum of Mathematics, Pi , Volume 3 , 2015 , e1
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/3.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author 2015

References

Bochnak, J., Coste, M. and Roy, M.-F., Real Algebraic Geometry, Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)], 36 (Springer, Berlin, 1998), translated from the 1987 French original, Revised by the authors.Google Scholar
Bhargava, M., ‘Most hyperelliptic curves over $\mathbb{Q}$ have no rational points’, Preprint.Google Scholar
Bhargava, M., ‘The density of discriminants of quintic rings and fields’, Ann. of Math. (2) 172(3) (2010), 1559–1591.Google Scholar
Bhargava, M. and Gross, B. H., ‘The average size of the 2-Selmer group of Jacobians of hyperelliptic curves having a rational Weierstrass point’, inAutomorphic Representations and L-functions, Tata Inst. Fundam. Res. Stud. Math., 22 (Tata Inst. Fund. Res., Mumbai, 2013), 23–91.Google Scholar
Borel, A., ‘Density and maximality of arithmetic subgroups’, J. reine angew. Math. 224 (1966), 78–89.Google Scholar
Borel, A., ‘Properties and linear representations of Chevalley groups’, inSeminar on Algebraic Groups and Related Finite Groups (The Institute for Advanced Study, Princeton, NJ, 1968/69), Lecture Notes in Mathematics, 131 (Springer, Berlin, 1970), 1–55.Google Scholar
Borel, A. and Harish-Chandra, ‘Arithmetic subgroups of algebraic groups’, Ann. of Math. (2) 75 (1962), 485–535.Google Scholar
Bosch, S., Lütkebohmert, W. and Raynaud, M., Néron Models, Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)], 21 (Springer, Berlin, 1990).Google Scholar
Bourbaki, N., Éléments de mathématique. Fasc. XXXIV. Groupes et algèbres de Lie. Chapitre IV: Groupes de Coxeter et systèmes de Tits. Chapitre V: Groupes engendrés par des réflexions. Chapitre VI: systèmes de racines, Actualités Scientifiques et Industrielles, No. 1337 (Hermann, Paris, 1968).Google Scholar
Bhargava, M. and Shankar, A., ‘Binary quartic forms having bounded invariants, and the boundedness of the average rank of elliptic curves’, Ann. of Math. (2) 181(1) (2015), 191–242.Google Scholar
Bruin, N. and Stoll, M., ‘Two-cover descent on hyperelliptic curves’, Math. Comput. 78(268) (2009), 2347–2370.Google Scholar
Clark, P. L. and Xarles, X., ‘Local bounds for torsion points on abelian varieties’, Canad. J. Math. 60(3) (2008), 532–555.Google Scholar
Kottwitz, R. E., ‘Transfer factors for Lie algebras’, Represent. Theory 3 (1999), 127–138. (electronic).Google Scholar
Lang, S., SL2(R) (Addison-Wesley Publishing Co., Reading, MA–London–Amsterdam, 1975).Google Scholar
Lorenzini, D., ‘Reduction of points in the group of components of the Néron model of a Jacobian’, J. reine angew. Math. 527 (2000), 117–150.Google Scholar
Lorenzini, D. and Tucker, T. J., ‘Thue equations and the method of Chabauty–Coleman’, Invent. Math. 148(1) (2002), 47–77.Google Scholar
Nakano, T. and Mori, T., ‘On the moduli space of pointed algebraic curves of low genus—a computational approach’, Tokyo J. Math. 27(1) (2004), 239–253.Google Scholar
Panyushev, D. I., ‘On invariant theory of 𝜃-groups’, J. Algebra 283(2) (2005), 655–670.Google Scholar
Platonov, V. and Rapinchuk, A., Algebraic Groups and Number Theory, Pure and Applied Mathematics, 139 (Academic Press Inc., Boston, MA, 1994), translated from the 1991 Russian original by Rachel Rowen.Google Scholar
Poonen, B. and Stoll, M., ‘Most odd degree hyperelliptic curves have only one rational point’, Ann. of Math. (2) 180(3) (2014), 1137–1166.Google Scholar
Reeder, M., ‘Torsion automorphisms of simple Lie algebras’, Enseign. Math. (2) 56(1–2) (2010), 3–47.Google Scholar
Springer, T. A., Linear Algebraic Groups, 2nd edn, Progress in Mathematics, 9 (Birkhäuser Boston, Inc., Boston, MA, 1998), 2009 edition (reprint).Google Scholar
Thorne, J. A., ‘On the 2-Selmer groups of plane quartic curves with a marked rational point’, Preprint.Google Scholar
Thorne, J. A., ‘Vinberg’s representations and arithmetic invariant theory’, Algebra Number Theory 7(9) (2013), 2331–2368.Google Scholar