Article contents
CLE PERCOLATIONS
Published online by Cambridge University Press: 03 October 2017
Abstract
Conformal loop ensembles (CLEs) are random collections of loops in a simply connected domain, whose laws are characterized by a natural conformal invariance property. The set of points not surrounded by any loop is a canonical random connected fractal set — a random and conformally invariant analog of the Sierpinski carpet or gasket.
In the present paper, we derive a direct relationship between the CLEs with simple loops (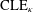 $\text{CLE}_{\unicode[STIX]{x1D705}}$ for
$\text{CLE}_{\unicode[STIX]{x1D705}}$ for 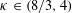 $\unicode[STIX]{x1D705}\in (8/3,4)$, whose loops are Schramm’s
$\unicode[STIX]{x1D705}\in (8/3,4)$, whose loops are Schramm’s 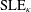 $\text{SLE}_{\unicode[STIX]{x1D705}}$-type curves) and the corresponding CLEs with nonsimple loops (
$\text{SLE}_{\unicode[STIX]{x1D705}}$-type curves) and the corresponding CLEs with nonsimple loops (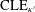 $\text{CLE}_{\unicode[STIX]{x1D705}^{\prime }}$ with
$\text{CLE}_{\unicode[STIX]{x1D705}^{\prime }}$ with 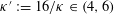 $\unicode[STIX]{x1D705}^{\prime }:=16/\unicode[STIX]{x1D705}\in (4,6)$, whose loops are
$\unicode[STIX]{x1D705}^{\prime }:=16/\unicode[STIX]{x1D705}\in (4,6)$, whose loops are 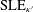 $\text{SLE}_{\unicode[STIX]{x1D705}^{\prime }}$-type curves). This correspondence is the continuum analog of the Edwards–Sokal coupling between the
$\text{SLE}_{\unicode[STIX]{x1D705}^{\prime }}$-type curves). This correspondence is the continuum analog of the Edwards–Sokal coupling between the 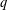 $q$-state Potts model and the associated FK random cluster model, and its generalization to noninteger
$q$-state Potts model and the associated FK random cluster model, and its generalization to noninteger 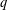 $q$.
$q$.
Like its discrete analog, our continuum correspondence has two directions. First, we show that for each 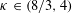 $\unicode[STIX]{x1D705}\in (8/3,4)$, one can construct a variant of
$\unicode[STIX]{x1D705}\in (8/3,4)$, one can construct a variant of 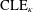 $\text{CLE}_{\unicode[STIX]{x1D705}}$ as follows: start with an instance of
$\text{CLE}_{\unicode[STIX]{x1D705}}$ as follows: start with an instance of 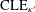 $\text{CLE}_{\unicode[STIX]{x1D705}^{\prime }}$, then use a biased coin to independently color each
$\text{CLE}_{\unicode[STIX]{x1D705}^{\prime }}$, then use a biased coin to independently color each 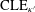 $\text{CLE}_{\unicode[STIX]{x1D705}^{\prime }}$ loop in one of two colors, and then consider the outer boundaries of the clusters of loops of a given color. Second, we show how to interpret
$\text{CLE}_{\unicode[STIX]{x1D705}^{\prime }}$ loop in one of two colors, and then consider the outer boundaries of the clusters of loops of a given color. Second, we show how to interpret 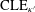 $\text{CLE}_{\unicode[STIX]{x1D705}^{\prime }}$ loops as interfaces of a continuum analog of critical Bernoulli percolation within
$\text{CLE}_{\unicode[STIX]{x1D705}^{\prime }}$ loops as interfaces of a continuum analog of critical Bernoulli percolation within 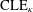 $\text{CLE}_{\unicode[STIX]{x1D705}}$ carpets — this is the first construction of continuum percolation on a fractal planar domain. It extends and generalizes the continuum percolation on open domains defined by
$\text{CLE}_{\unicode[STIX]{x1D705}}$ carpets — this is the first construction of continuum percolation on a fractal planar domain. It extends and generalizes the continuum percolation on open domains defined by 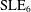 $\text{SLE}_{6}$ and
$\text{SLE}_{6}$ and 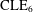 $\text{CLE}_{6}$.
$\text{CLE}_{6}$.
These constructions allow us to prove several conjectures made by the second author and provide new and perhaps surprising interpretations of the relationship between CLEs and the Gaussian free field. Along the way, we obtain new results about generalized 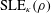 $\text{SLE}_{\unicode[STIX]{x1D705}}(\unicode[STIX]{x1D70C})$ curves for
$\text{SLE}_{\unicode[STIX]{x1D705}}(\unicode[STIX]{x1D70C})$ curves for 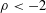 $\unicode[STIX]{x1D70C}<-2$, such as their decomposition into collections of
$\unicode[STIX]{x1D70C}<-2$, such as their decomposition into collections of 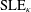 $\text{SLE}_{\unicode[STIX]{x1D705}}$-type ‘loops’ hanging off of
$\text{SLE}_{\unicode[STIX]{x1D705}}$-type ‘loops’ hanging off of 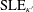 $\text{SLE}_{\unicode[STIX]{x1D705}^{\prime }}$-type ‘trunks’, and vice versa (exchanging
$\text{SLE}_{\unicode[STIX]{x1D705}^{\prime }}$-type ‘trunks’, and vice versa (exchanging  $\unicode[STIX]{x1D705}$ and
$\unicode[STIX]{x1D705}$ and 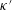 $\unicode[STIX]{x1D705}^{\prime }$). We also define a continuous family of natural
$\unicode[STIX]{x1D705}^{\prime }$). We also define a continuous family of natural 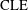 $\text{CLE}$ variants called boundary conformal loop ensembles (BCLEs) that share some (but not all) of the conformal symmetries that characterize
$\text{CLE}$ variants called boundary conformal loop ensembles (BCLEs) that share some (but not all) of the conformal symmetries that characterize 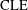 $\text{CLE}$s, and that should be scaling limits of critical models with special boundary conditions. We extend the
$\text{CLE}$s, and that should be scaling limits of critical models with special boundary conditions. We extend the  $\text{CLE}_{\unicode[STIX]{x1D705}}$/
$\text{CLE}_{\unicode[STIX]{x1D705}}$/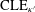 $\text{CLE}_{\unicode[STIX]{x1D705}^{\prime }}$ correspondence to a
$\text{CLE}_{\unicode[STIX]{x1D705}^{\prime }}$ correspondence to a 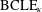 $\text{BCLE}_{\unicode[STIX]{x1D705}}$/
$\text{BCLE}_{\unicode[STIX]{x1D705}}$/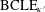 $\text{BCLE}_{\unicode[STIX]{x1D705}^{\prime }}$ correspondence that makes sense for the wider range
$\text{BCLE}_{\unicode[STIX]{x1D705}^{\prime }}$ correspondence that makes sense for the wider range 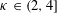 $\unicode[STIX]{x1D705}\in (2,4]$ and
$\unicode[STIX]{x1D705}\in (2,4]$ and 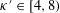 $\unicode[STIX]{x1D705}^{\prime }\in [4,8)$.
$\unicode[STIX]{x1D705}^{\prime }\in [4,8)$.
- Type
- Research Article
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author(s) 2017
References
- 24
- Cited by



