Article contents
Refined stability thresholds for localized spot patterns for the Brusselator model in  $\mathbb{R}^2$
$\mathbb{R}^2$
Published online by Cambridge University Press: 30 July 2018
Abstract
In the singular perturbation limit ε → 0, we analyse the linear stability of multi-spot patterns on a bounded 2-D domain, with Neumann boundary conditions, as well as periodic patterns of spots centred at the lattice points of a Bravais lattice in  $\mathbb{R}^2$, for the Brusselator reaction–diffusion model
$\mathbb{R}^2$, for the Brusselator reaction–diffusion model
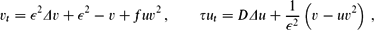 $$
\begin{equation*}
v_t = \epsilon^2 \Delta v + \epsilon^2 - v + fu v^2 \,, \qquad \tau
u_t = D \Delta u + \frac{1}{\epsilon^2}\left(v - u v^2\right) \,,
\end{equation*}
$$
$$
\begin{equation*}
v_t = \epsilon^2 \Delta v + \epsilon^2 - v + fu v^2 \,, \qquad \tau
u_t = D \Delta u + \frac{1}{\epsilon^2}\left(v - u v^2\right) \,,
\end{equation*}
$$ ${\mathcal O}$(ν−1), where ν = −1/log ϵ, based on a rigorous analysis of a non-local eigenvalue problem (NLEP), predicts that zero-eigenvalue crossings are degenerate. To unfold this degeneracy, the conventional leading-order-in-ν NLEP linear stability theory for spot amplitude instabilities is extended to one higher order in the logarithmic gauge ν. For a multi-spot pattern on a finite domain under a certain symmetry condition on the spot configuration, or for a periodic pattern of spots centred at the lattice points of a Bravais lattice in
${\mathcal O}$(ν−1), where ν = −1/log ϵ, based on a rigorous analysis of a non-local eigenvalue problem (NLEP), predicts that zero-eigenvalue crossings are degenerate. To unfold this degeneracy, the conventional leading-order-in-ν NLEP linear stability theory for spot amplitude instabilities is extended to one higher order in the logarithmic gauge ν. For a multi-spot pattern on a finite domain under a certain symmetry condition on the spot configuration, or for a periodic pattern of spots centred at the lattice points of a Bravais lattice in 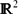 $\mathbb{R}^2$, our extended NLEP theory provides explicit and improved analytical predictions for the critical value of the inhibitor diffusivity D at which a competition instability, due to a zero-eigenvalue crossing, will occur. Finally, when D is below the competition stability threshold, a different extension of conventional NLEP theory is used to determine an explicit scaling law, with anomalous dependence on ϵ, for the Hopf bifurcation threshold value of τ that characterizes temporal oscillations in the spot amplitudes.
$\mathbb{R}^2$, our extended NLEP theory provides explicit and improved analytical predictions for the critical value of the inhibitor diffusivity D at which a competition instability, due to a zero-eigenvalue crossing, will occur. Finally, when D is below the competition stability threshold, a different extension of conventional NLEP theory is used to determine an explicit scaling law, with anomalous dependence on ϵ, for the Hopf bifurcation threshold value of τ that characterizes temporal oscillations in the spot amplitudes.
Keywords
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2018
Footnotes
†Michael J. Ward and Juncheng Wei were supported by NSERC Discovery grants. Justin Tzou was partially supported by a PIMS CRG Postdoctoral Fellowship. Yifan Chang was supported by a graduate research stipend while at UBC.
References
- 5
- Cited by


