No CrossRef data available.
Article contents
Steady states of thin-film equations with van der Waals force with mass constraint
Published online by Cambridge University Press: 30 May 2022
Abstract
We consider steady states with mass constraint of the fourth-order thin-film equation with van der Waals force in a bounded domain which leads to a singular elliptic equation for the thickness with an unknown pressure term. By studying second-order nonlinear ordinary differential equation,
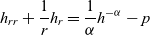 \begin{equation*}h_{rr}+\frac{1}{r}h_{r}=\frac{1}{\alpha}h^{-\alpha}-p\end{equation*}
\begin{equation*}h_{rr}+\frac{1}{r}h_{r}=\frac{1}{\alpha}h^{-\alpha}-p\end{equation*}
MSC classification
- Type
- Papers
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press



