Hostname: page-component-76fb5796d-2lccl Total loading time: 0 Render date: 2024-04-25T13:05:17.559Z Has data issue: false hasContentIssue false
  • English
  • Français

Polynomial deviation bounds for recurrent Harris processes having general state space

Published online by Cambridge University Press:  08 February 2013

Eva Löcherbach  and
Dasha Loukianova
Eva Löcherbach
Affiliation:
CNRS UMR 8088, Département de Mathématiques, Université de Cergy-Pontoise, 95000 Cergy-Pontoise, France. eva.loecherbach@u-cergy.fr
Dasha Loukianova
Affiliation:
Département de Mathématiques, Université d’Evry-Val d’Essonne, Bd François Mitterrand, 91025 Evry Cedex, France; dasha.loukianova@univ-evry.fr
Get access

Abstract

Consider a strong Markov process in continuous time, taking values in some Polish state space. Recently, Douc et al. [Stoc. Proc. Appl. 119, (2009) 897–923] introduced verifiable conditions in terms of a supermartingale property implying an explicit control of modulated moments of hitting times. We show how this control can be translated into a control of polynomial moments of abstract regeneration times which are obtained by using the regeneration method of Nummelin, extended to the time-continuous context. As a consequence, if a p-th moment of the regeneration times exists, we obtain non asymptotic deviation bounds of the form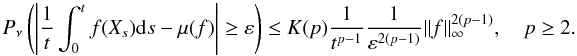

\begin{equation*} P_{\nu} \left (\left|\frac1t\int_0^tf(X_s){\rm d}s-\mu(f)\right|\geq\ge\right)\leq K(p)\frac1{t^{p- 1}}\frac 1{\ge^{2(p-1)}}\|f\|_\infty^{2(p-1)} ,\quad p \geq 2. \end{equation*}Pν1t∫0tf(Xs)ds−μ(f)≥ε≤K(p)1tp−11ε2(p−1)∥f∥∞2(p−1),p≥2.
Here, f is a bounded function and μ is the invariant measure of the process. We give several examples, including elliptic stochastic differential equations and stochastic differential equations driven by a jump noise.

Keywords

Harris recurrencepolynomial ergodicityNummelin splittingcontinuous time Markov processesdrift conditionmodulated moment
Type
Research Article
Information
ESAIM: Probability and Statistics , Volume 17 , 2013 , pp. 195 - 218
Copyright
© EDP Sciences, SMAI, 2013

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adamczak, R., A tail inequality for suprema of unbounded empirical processes with applications to Markov chains. Electron. J. Probab. 13 (2008) 1000–1034. Google Scholar
Athreya, K.B. and Ney, P., A new approach to the limit theory of recurrent Markov chains. Trans. Amer. Math. Soc. 245 (1978) 493–501. Google Scholar
Bertail, P. and Clémençon, S., Sharp bounds for the tails of functionals of markov chains, Teor. Veroyatnost. i Primenen 54 (2009) 609–619. Google Scholar
Cattiaux, P. and Guillin, A., Deviation bounds for additive functionals of Markov processes. ESAIM : PS 12 (2008) 12–29. Google Scholar
Chazottes, J.-R., Collet, P., Külske, C. and Redig, F., Concentration inequalities for random fields via coupling. Probab. Theory Relat. Fields 137 (2007) 201–225. Google Scholar
Clémençon, S., Moment and probability inequalities for sums of bounded additive functionals of regular Markov chains via the Nummelin splitting technique. Stat. Probab. Lett. 55 (2001) 227–238. Google Scholar
Douc, R., Fort, G. and Guillin, A., Subgeometric rates of convergence of f-ergodic strong Markov processes. Stoch. Proc. Appl. 119 (2009) 897–923. Google Scholar
Douc, R., Fort, G., Moulines, E. and Soulier, P., Practical drift conditions for subgeometric rates of convergence. Ann. Appl. Probab. 14 (2004) 1353–1377. Google Scholar
Fort, G. and Roberts, G.O., Subgeometric ergodicity of strong Markov processes. Ann. Appl. Probab. 15 (2005) 1565–1589. Google Scholar
Guillin, A., Léonard, C., Wu, L. and Yao, N., Transportation-information inequalities for Markov processes. Probab. Theory Relat. Fields 144 (2009) 669–695. Google Scholar
Kulik, A.M., Exponential ergodicity of the solutions to SDE’s with a jump noise. Stoch. Proc. Appl. 119 (2009) 602–632. Google Scholar
Kusuoka, S. and Stroock, D., Applications of the Malliavin calculus. III. J. Fac. Sci., Univ. Tokyo, Sect. I A 34 (1987) 391–442. Google Scholar
R. Höpfner and E. Löcherbach, Limit theorems for null recurrent Markov processes. Memoirs AMS 161 (2003).
Lezaud, P., Chernoff and Berry-Esséen inequalities for Markov processes. ESAIM : PS 5 (2001) 183–201. Google Scholar
Löcherbach, E. and Loukianova, D., On Nummelin splitting for continuous time Harris recurrent Markov processes and application to kernel estimation for multi-dimensional diffusions. Stoch. Proc. Appl. 118 (2008) 1301–1321. Google Scholar
Löcherbach, E., Loukianova, D. and Loukianov, O., Deviation bounds in ergodic theorem for positively recurrent one-dimensional diffusions and integrability of hitting times. Ann. Inst. Henri Poincaré 47 (2011) 425–449. Google Scholar
Nummelin, E., A splitting technique for Harris recurrent Markov chains. Z. Wahrscheinlichkeitstheorie Verw. Geb. 43 (1978) 309–318. Google Scholar
S. Pal, Concentration for multidimensional diffusions and their boundary local times. To appear in Probab. Theory Relat. Fields (2011), DOI 10.1007/s00440-011-0368-1
D. Revuz, Markov chains, Revised edition. Amsterdam, North Holland (1984).
E. Rio, Théorie asymptotique des processus aléatoires faiblement dépendants. Springer. Math. Appl. 31 (2000).
Simon, T., Support theorem for jump processes. Stoch. Proc. Appl. 89 (2000) 1–30. Google Scholar
Veretennikov, A.Yu., On polynomial mixing bounds for stochastic differential equations. Stoch. Proc. Appl. 70 (1997) 115–127. Google Scholar
Veretennikov, A.Yu. and Klokov, S.A., On subexponential mixing rate for Markov processes. Teor. Veroyatnost. i Primenen 49 (2004) 21–35. Google Scholar
Wu, L., A deviation inequality for non-reversible Markov process, Ann. Inst. Henri Poincaré 36 (2000) 435–445. Google Scholar