Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Bigot, Jérémie
and
Gendre, Xavier
2013.
Minimax properties of Fréchet means of discretely sampled curves.
The Annals of Statistics,
Vol. 41,
Issue. 2,
Awate, Suyash P.
Yu, Yen-Yun
and
Whitaker, Ross T.
2014.
Machine Learning and Knowledge Discovery in Databases.
Vol. 8724,
Issue. ,
p.
82.
Arnaudon, Marc
and
Miclo, Laurent
2014.
A stochastic algorithm finding generalized means on compact manifolds.
Stochastic Processes and their Applications,
Vol. 124,
Issue. 10,
p.
3463.
Huckemann, Stephan
and
Hotz, Thomas
2014.
On Means and Their Asymptotics: Circles and Shape Spaces.
Journal of Mathematical Imaging and Vision,
Vol. 50,
Issue. 1-2,
p.
98.
Arnaudon, Marc
and
Miclo, Laurent
2016.
A stochastic algorithm finding $p$-means on the circle.
Bernoulli,
Vol. 22,
Issue. 4,
Devilliers, Loïc
Allassonnière, Stéphanie
Trouvé, Alain
and
Pennec, Xavier
2017.
Inconsistency of Template Estimation by Minimizing of the Variance/Pre-Variance in the Quotient Space.
Entropy,
Vol. 19,
Issue. 6,
p.
288.
Nguyen, Tien Dat
Pham Ngoc, Thanh Mai
and
Rivoirard, Vincent
2023.
Adaptive warped kernel estimation for nonparametric regression with circular responses.
Electronic Journal of Statistics,
Vol. 17,
Issue. 2,
Le, Chon Van
and
Pham, Uyen Hoang
2024.
A prelude to statistics in Wasserstein metric spaces.
Asian Journal of Economics and Banking,
Vol. 8,
Issue. 1,
p.
54.
Faugeras, Olivier
2024.
An Invitation to Intrinsic Compositional Data Analysis Using Projective Geometry and Hilbert’s Metric.
SSRN Electronic Journal,
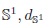 S1,dS1) be the unit circle in ℝ2 endowed with the arclength distance. We give a sufficient and necessary condition for a general probability measure μ to admit a well defined Fréchet mean on (\hbox{$\mathbb{S}^1,d_{\mathbb{S}^1}$}
S1,dS1) be the unit circle in ℝ2 endowed with the arclength distance. We give a sufficient and necessary condition for a general probability measure μ to admit a well defined Fréchet mean on (\hbox{$\mathbb{S}^1,d_{\mathbb{S}^1}$}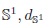 S1,dS1). We derive a new sufficient condition of existence P(α, ϕ) with no restriction on the support of the measure. Then, we study the convergence of the empirical Fréchet mean to the Fréchet mean and we give an algorithm to compute it.
S1,dS1). We derive a new sufficient condition of existence P(α, ϕ) with no restriction on the support of the measure. Then, we study the convergence of the empirical Fréchet mean to the Fréchet mean and we give an algorithm to compute it.

