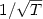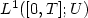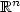Research Article
Exponential stabilization of nonlinear driftless systems with robustness to unmodeled dynamics
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 1-35
-
- Article
- Export citation
Well posedness and control of semilinear wave equations with iterated logarithms
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 37-56
-
- Article
- Export citation
Control of networks of Euler-Bernoulli beams
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 57-81
-
- Article
- Export citation
Approximate controllability and its well-posedness for the semilinear reaction-diffusion equation with internal lumped controls
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 83-98
-
- Article
- Export citation
Input-to-state stability with respect to measurement disturbances for one-dimensional systems
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 99-121
-
- Article
- Export citation
Stabilization of a hybrid system with a nonlinear nonmonotone feedback
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 123-135
-
- Article
- Export citation
Rank-2 distributions satisfying the Goursat condition: all their local models in dimension 7 and 8
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 137-158
-
- Article
- Export citation
Approximation of control problems involving ordinary and impulsive controls
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 159-176
-
- Article
- Export citation
Analytic controllability of the wave equation over a cylinder
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 177-207
-
- Article
- Export citation
Boundary layer tails in periodic homogenization
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 209-243
-
- Article
- Export citation
Méthodes géométriques et analytiques pour étudier l'application exponentielle, la sphère et le front d'onde en géométrie sous-riemannienne dans le cas Martinet
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 245-334
-
- Article
- Export citation
Approximation of viscosity solution by morphological filters
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 335-359
-
- Article
- Export citation
Stability and Stabilization of Discontinuous Systems and Nonsmooth Lyapunov Functions
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 361-376
-
- Article
- Export citation
Sub-Riemannian Metrics: Minimality of Abnormal Geodesics versus Subanalyticity
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 377-403
-
- Article
- Export citation
Control Norms for Large Control Times
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 405-418
-
- Article
- Export citation
A new method to obtain decay rate estimates for dissipative systems
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 419-444
-
- Article
- Export citation
Patchy Vector Fields and Asymptotic Stabilization
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 445-471
-
- Article
- Export citation
a functional analysis model for natural images permitting structured compression
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 473-495
-
- Article
- Export citation
Approximate controllability for a linear model of fluid structure interaction
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 497-513
-
- Article
- Export citation
Nonlinear feedback stabilization of a rotating body-beam without damping
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 515-535
-
- Article
- Export citation