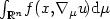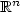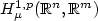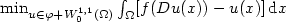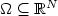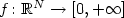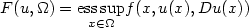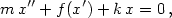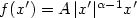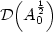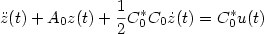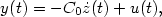Research Article
The tree of shapes of an image
-
- Published online by Cambridge University Press:
- 15 September 2003, pp. 1-18
-
- Article
- Export citation
Design-dependent loads in topology optimization
-
- Published online by Cambridge University Press:
- 15 September 2003, pp. 19-48
-
- Article
- Export citation
Boundary integral formulae for the reconstruction of electric and electromagnetic inhomogeneities of small volume
-
- Published online by Cambridge University Press:
- 15 September 2003, pp. 49-66
-
- Article
- Export citation
Nonlinear observers in reflexive Banach spaces
-
- Published online by Cambridge University Press:
- 15 September 2003, pp. 67-103
-
- Article
- Export citation
Lower semicontinuity of multiple µ-quasiconvex integrals
-
- Published online by Cambridge University Press:
- 15 September 2003, pp. 105-124
-
- Article
- Export citation
Geometric constraints on the domain for a class of minimum problems
-
- Published online by Cambridge University Press:
- 15 September 2003, pp. 125-133
-
- Article
- Export citation
On the Lower Semicontinuity of Supremal Functionals
-
- Published online by Cambridge University Press:
- 15 September 2003, pp. 135-143
-
- Article
- Export citation
A Variational Problem Modelling Behavior of Unorthodox Silicon Crystals
-
- Published online by Cambridge University Press:
- 15 September 2003, pp. 145-149
-
- Article
- Export citation
An algebraic framework for linear identification
-
- Published online by Cambridge University Press:
- 15 September 2003, pp. 151-168
-
- Article
- Export citation
Systems with hysteresis in the feedback loop: existence, regularity and asymptotic behaviour of solutions
-
- Published online by Cambridge University Press:
- 15 September 2003, pp. 169-196
-
- Article
- Export citation
Feedback stabilization of Navier–Stokes equations
-
- Published online by Cambridge University Press:
- 15 September 2003, pp. 197-205
-
- Article
- Export citation
Controllability for Systems with Slowly Varying Parameters
-
- Published online by Cambridge University Press:
- 15 September 2003, pp. 207-216
-
- Article
- Export citation
Optimal design of turbines with an attached mass
-
- Published online by Cambridge University Press:
- 15 September 2003, pp. 217-230
-
- Article
- Export citation
The Nonlinearly Damped Oscillator
-
- Published online by Cambridge University Press:
- 15 September 2003, pp. 231-246
-
- Article
- Export citation
How to get a conservative well-posed linear system out of thin air. Part I. Well-posedness and energy balance
-
- Published online by Cambridge University Press:
- 15 September 2003, pp. 247-273
-
- Article
- Export citation
Motion Planning for a nonlinear Stefan Problem
-
- Published online by Cambridge University Press:
- 15 September 2003, pp. 275-296
-
- Article
- Export citation
Analyse de récession et résultats de stabilité d'une convergence variationnelle, application à la théorie de la dualité en programmation mathématique
-
- Published online by Cambridge University Press:
- 15 September 2003, pp. 297-315
-
- Article
- Export citation
Orlicz capacities and applications to some existence questions for elliptic pdes having measure data
-
- Published online by Cambridge University Press:
- 15 September 2003, pp. 317-341
-
- Article
- Export citation
On The Stabilizability of Homogeneous Systems Of Odd Degree
-
- Published online by Cambridge University Press:
- 15 September 2003, pp. 343-352
-
- Article
- Export citation
Nonlinear observers for locally uniformly observable systems
-
- Published online by Cambridge University Press:
- 15 September 2003, pp. 353-370
-
- Article
- Export citation