Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Fonseca, I.
Fusco, N.
Leoni, G.
and
Morini, M.
2007.
Equilibrium Configurations of Epitaxially Strained Crystalline Films: Existence and Regularity Results.
Archive for Rational Mechanics and Analysis,
Vol. 186,
Issue. 3,
p.
477.
Braides, Andrea
and
Riey, Giuseppe
2008.
A variational model in image processing with focal points.
ESAIM: Mathematical Modelling and Numerical Analysis,
Vol. 42,
Issue. 5,
p.
729.
SOLCI, MARGHERITA
2009.
HOMOGENIZATION OF ENERGIES DEFINED ON PAIRS SET-FUNCTION.
Communications in Contemporary Mathematics,
Vol. 11,
Issue. 03,
p.
459.
Fonseca, Irene
Fusco, Nicola
Leoni, Giovanni
and
Millot, Vincent
2011.
Material voids in elastic solids with anisotropic surface energies.
Journal de Mathématiques Pures et Appliquées,
Vol. 96,
Issue. 6,
p.
591.
Burton, G. R.
and
Toland, J. F.
2011.
Surface waves on steady perfect‐fluid flows with vorticity.
Communications on Pure and Applied Mathematics,
Vol. 64,
Issue. 7,
p.
975.
Bonacini, Marco
2013.
Epitaxially strained elastic films: the case of anisotropic surface energies.
ESAIM: Control, Optimisation and Calculus of Variations,
Vol. 19,
Issue. 1,
p.
167.
Babadjian, Jean-François
and
Millot, Vincent
2014.
Unilateral gradient flow of the Ambrosio–Tortorelli functional by minimizing movements.
Annales de l'Institut Henri Poincaré C, Analyse non linéaire,
Vol. 31,
Issue. 4,
p.
779.
Goldman, M.
and
Zwicknagl, B.
2014.
Scaling Law and Reduced Models for Epitaxially Strained Crystalline Films.
SIAM Journal on Mathematical Analysis,
Vol. 46,
Issue. 1,
p.
1.
Henao, Duvan
Mora-Corral, Carlos
and
Xu, Xianmin
2015.
Γ-convergence Approximation of Fracture and Cavitation in Nonlinear Elasticity.
Archive for Rational Mechanics and Analysis,
Vol. 216,
Issue. 3,
p.
813.
Henao, Duvan
Mora-Corral, Carlos
and
Xu, Xianmin
2016.
A numerical study of void coalescence and fracture in nonlinear elasticity.
Computer Methods in Applied Mechanics and Engineering,
Vol. 303,
Issue. ,
p.
163.
Leoni, Giovanni
2016.
Free Discontinuity Problems.
p.
69.
Fonseca, I.
Leoni, G.
and
Morini, M.
2017.
Equilibria and dislocations in epitaxial growth.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 154,
Issue. ,
p.
88.
Chambolle, Antonin
Conti, Sergio
and
Francfort, Gilles A.
2018.
Approximation of a Brittle Fracture Energy with a Constraint of Non-interpenetration.
Archive for Rational Mechanics and Analysis,
Vol. 228,
Issue. 3,
p.
867.
Fonseca, I.
Fusco, N.
Leoni, G.
and
Morini, M.
2018.
A model for dislocations in epitaxially strained elastic films.
Journal de Mathématiques Pures et Appliquées,
Vol. 111,
Issue. ,
p.
126.
Fusco, Nicola
Julin, Vesa
and
Morini, Massimiliano
2018.
The Surface Diffusion Flow with Elasticity in the Plane.
Communications in Mathematical Physics,
Vol. 362,
Issue. 2,
p.
571.
Kholmatov, Shokhrukh Yu.
and
Piovano, Paolo
2020.
A Unified Model for Stress-Driven Rearrangement Instabilities.
Archive for Rational Mechanics and Analysis,
Vol. 238,
Issue. 1,
p.
415.
Crismale, Vito
and
Friedrich, Manuel
2020.
Equilibrium Configurations for Epitaxially Strained Films and Material Voids in Three-Dimensional Linear Elasticity.
Archive for Rational Mechanics and Analysis,
Vol. 237,
Issue. 2,
p.
1041.
Fusco, Nicola
Julin, Vesa
and
Morini, Massimiliano
2020.
The Surface Diffusion Flow with Elasticity in Three Dimensions.
Archive for Rational Mechanics and Analysis,
Vol. 237,
Issue. 3,
p.
1325.
Belz, Sandro
and
Bredies, Kristian
2021.
Approximation of the Mumford–Shah functional by phase fields of bounded variation.
Analysis and Applications,
Vol. 19,
Issue. 02,
p.
183.
Goldman, Michael
Merlet, Benoit
and
Millot, Vincent
2021.
A Ginzburg–Landau model with topologically induced free discontinuities.
Annales de l'Institut Fourier,
Vol. 70,
Issue. 6,
p.
2583.
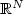 ,
energies depending on the perimeter of a subset $E\subset\Omega$
,
energies depending on the perimeter of a subset $E\subset\Omega$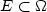 (or some equivalent surface integral) and on a function u which is
defined only on $\Omega\setminus E$
(or some equivalent surface integral) and on a function u which is
defined only on $\Omega\setminus E$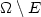 . We compute the lower semicontinuous envelope
of such energies. This relaxation has to take into
account the fact that in the limit, the “holes” E may
collapse into a discontinuity of u, whose surface will be counted
twice in the relaxed energy. We discuss some situations where such
energies appear, and give, as an application, a new proof
of convergence for an extension
of Ambrosio-Tortorelli's approximation to the Mumford-Shah functional.
. We compute the lower semicontinuous envelope
of such energies. This relaxation has to take into
account the fact that in the limit, the “holes” E may
collapse into a discontinuity of u, whose surface will be counted
twice in the relaxed energy. We discuss some situations where such
energies appear, and give, as an application, a new proof
of convergence for an extension
of Ambrosio-Tortorelli's approximation to the Mumford-Shah functional.


