Hostname: page-component-76fb5796d-45l2p Total loading time: 0 Render date: 2024-04-26T04:33:39.439Z Has data issue: false hasContentIssue false
  • English
  • Français

Regularity and variationality of solutions to Hamilton-Jacobi equations. Part I: Regularity

Published online by Cambridge University Press:  15 June 2004

Andrea C.G. Mennucci
Andrea C.G. Mennucci*
Affiliation:
Scuola Normale Superiore Piazza dei Cavalieri 7, 56126 Pisa, Italy; a.mennuci@sns.it.
Get access

Abstract

We formulate an Hamilton-Jacobi partial differential equation H( x, D u(x))=0 on a n dimensional manifold M, with assumptions of convexity of H(x, .) and regularity of H (locally in a neighborhood of {H=0} in T*M); we define the “minsol solution” u, a generalized solution; to this end, we view T*M as a symplectic manifold. The definition of “minsol solution” is suited to proving regularity results about u; in particular, we prove in the first part that the closure of the set where u is not regular may be covered by a countable number of $n-1$ 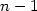dimensional manifolds, but for a ${{\mathcal H}}^{n-1}$ 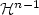negligeable subset. These results can be applied to the cutlocus of a C2 submanifold of a Finsler manifold.

Keywords

Hamilton-Jacobi equationsconjugate points.
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 10 , Issue 3 , July 2004 , pp. 426 - 451
Copyright
© EDP Sciences, SMAI, 2004

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alberti, G., On the structure of singular sets of convex functions. Calc. Var. Partial Differ. Equ. 2 (1994) 17-27. CrossRef
A. Ambrosetti and G. Prodi, A primer of nonlinear analysis. Cambridge University Press, Cambridge (1993).
L. Ambrosio, P. Cannarsa and H.M. Soner, On the propagation of singularities of semi-convex functions. Ann. Scuola. Norm. Sup. Pisa XX (1993) 597-616.
Cannarsa, P., Mennucci, A. and Sinestrari, C., Regularity results for solutions of a class of Hamilton-Jacobi equations. Arch. Ration. Mech. Anal. 140 (1997) 197-223 (or, preprint 13-95 Dip. Mat. Univ Tor Vergata, Roma). CrossRef
R. Courant and D. Hilbert, Methods of Mathematical Physics, volume II. Interscience, New York (1963).
T. Djaferis and I. Schick, Eds., Advances in System Theory. Kluwer Academic Publishers Boston, October (1999).
L.C. Evans, Partial Differential Equations. A.M.S. Grad. Stud. Math. 19 (2002).
H. Federer, Geometric measure theory. Springer-Verlag, Berlin (1969).
W.H. Fleming and H.M. Soner, Controlled Markov processes and viscosity solutions. Springer-Verlag, Berlin (1993).
P. Hartman, Ordinary Differential Equations. Wiley, New York (1964).
Itoh, J. and Tanaka, M., The Lipschitz continuity of the distance function to the cut locus. Trans. Amer. Math. Soc. 353 (2000) 21-40. CrossRef
Kružhkov, S.N., The cauchy problem in the large for certain non-linear first order differential equations. Soviet Math. Dockl. 1 (1960) 474-475.
Yan yan Li and L. Nirenberg, The distance function to the boundary, finsler geometry and the singular set of viscosity solutions of some Hamilton-Jacobi equations (2003) (preprint).
P.L. Lions, Generalized Solutions of Hamilton-Jacobi Equations. Pitman, Boston (1982).
Mantegazza, C. and Mennucci, A.C., Hamilton-Jacobi equations and distance functions on Riemannian manifolds. Appl. Math. Optim. 47 (2003) 1-25. CrossRef
D. McDuff and D. Salomon, Introduction to Symplectic Topology. Oxford Mathematical Monograph, Oxford University Press, Clarendon Press, Oxford (1995).
A.C.G. Mennucci, Regularity and variationality of solutions to Hamilton-Jacobi equations. Part ii: variationality, existence, uniqueness (in preparation).
C. Sinestrari and P. Cannarsa, Semiconcave functions, Hamilton-Jacobi equations and optimal control problems, in Progress in Nonlinear Differential Equations and Their Applications, Vol. 58, Birkhauser Boston (2004).
G.J. Galloway, P.T. Chruściel, J.H.G. Fu and R. Howard, On fine differentiability properties of horizons and applications to Riemannian geometry (to appear).
Pignotti, C., Rectifiability results for singular and conjugate points of optimal exit time problems. J. Math. Anal. Appl. 270 (2002) 681-708. CrossRef
L. Simon, Lectures on Geometric Measure Theory, Vol. 3 of Proc. Center for Mathematical Analysis. Australian National University, Canberra (1983).
Y. Yomdin, β-spreads of sets in metric spaces and critical values of smooth functions.
Yomdin, Y., The geometry of critical and near-critical values of differential mappings. Math. Ann. 4 (1983) 495-515. CrossRef
Y. Yomdin, Metric properties of semialgebraic sets and mappings and their applications in smooth analysis, in Géométrie algébrique et applications, III (la Rábida, 1984), Herman, Paris (1987) 165-183.