Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Michaille, Gérard
and
Valadier, Michel
2002.
Young measures generated by a class of integrands: a narrow epicontinuity and applications to Homogenization.
Journal de Mathématiques Pures et Appliquées,
Vol. 81,
Issue. 12,
p.
1277.
Fonseca, Irene
and
Leoni, Giovanni
2002.
Variational Methods for Discontinuous Structures.
p.
117.
Kirchheim, Bernd
Müller, Stefan
and
Šverák, Vladimír
2003.
Geometric Analysis and Nonlinear Partial Differential Equations.
p.
347.
Pisante, Giovanni
2004.
Homogenization of micromagnetics large bodies.
ESAIM: Control, Optimisation and Calculus of Variations,
Vol. 10,
Issue. 2,
p.
295.
Gargiulo, Giuliano
Zappale, Elvira
and
Zorgati, Hamdi
2007.
Modélisation de films courbés non simples de second gradient.
Comptes Rendus. Mathématique,
Vol. 344,
Issue. 5,
p.
343.
Ansini, Nadia
and
Garroni, Adriana
2007.
Γ-convergence of functionals on divergence-free fields.
ESAIM: Control, Optimisation and Calculus of Variations,
Vol. 13,
Issue. 4,
p.
809.
Bocea, Marian
and
Nesi, Vincenzo
2008.
$\Gamma$-Convergence of Power-Law Functionals, Variational Principles in $L^{\infty},$ and Applications.
SIAM Journal on Mathematical Analysis,
Vol. 39,
Issue. 5,
p.
1550.
Serrano, Hélia
2009.
On Γ-convergence in divergence-free fields through Young measures.
Journal of Mathematical Analysis and Applications,
Vol. 359,
Issue. 1,
p.
311.
Fonseca, Irene
and
Kružík, Martin
2010.
Oscillations and concentrations generated by ${\mathcal A}$-free mappings and weak lower semicontinuity of integral functionals.
ESAIM: Control, Optimisation and Calculus of Variations,
Vol. 16,
Issue. 2,
p.
472.
Cesana, Pierluigi
2010.
Relaxation of Multiwell Energies in Linearized Elasticity and Applications to Nematic Elastomers.
Archive for Rational Mechanics and Analysis,
Vol. 197,
Issue. 3,
p.
903.
Serrano, Hélia
2011.
Reiterated homogenization of the vector potential formulation of a magnetostatic problem in anisotropic composite media.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 74,
Issue. 18,
p.
7380.
Kreisbeck, Carolin
2012.
Another approach to the thin-film Γ-limit of the micromagnetic free energy in the regime of small samples.
Quarterly of Applied Mathematics,
Vol. 71,
Issue. 2,
p.
201.
Serrano, Hélia
2012.
Γ-convergence of multiscale periodic functionals depending on the time-derivative and the curl operator.
Journal of Mathematical Analysis and Applications,
Vol. 387,
Issue. 2,
p.
1024.
Baía, Margarida
Chermisi, Milena
Matias, José
and
Santos, Pedro M.
2013.
Lower semicontinuity and relaxation of signed functionals with linear growth in the context of $${\mathcal A}$$ -quasiconvexity.
Calculus of Variations and Partial Differential Equations,
Vol. 47,
Issue. 3-4,
p.
465.
Ribeiro, Ana Margarida
and
Zappale, Elvira
2013.
Relaxation of certain integral functionals depending on strain and chemical composition.
Chinese Annals of Mathematics, Series B,
Vol. 34,
Issue. 4,
p.
491.
Zeppieri, Caterina Ida
Ansini, Nadia
and
Dal Maso, Gianni
2014.
New results on Γ-limits of integral functionals.
Annales de l'Institut Henri Poincaré C, Analyse non linéaire,
Vol. 31,
Issue. 1,
p.
185.
Ansini, Nadia
and
Prinari, Francesca
2014.
Power-Law Approximation under Differential Constraints.
SIAM Journal on Mathematical Analysis,
Vol. 46,
Issue. 2,
p.
1085.
Serrano, Hélia
2014.
A variational approach to the homogenization of laminate metamaterials.
Nonlinear Analysis: Real World Applications,
Vol. 18,
Issue. ,
p.
75.
Matias, José
and
Morandotti, Marco
2015.
Homogenization problems in the calculus of variations: an overview.
São Paulo Journal of Mathematical Sciences,
Vol. 9,
Issue. 2,
p.
162.
Matias, José
Morandotti, Marco
and
Santos, Pedro M.
2015.
Homogenization of Functionals with Linear Growth in the Context of $$\mathcal A$$ A -quasiconvexity.
Applied Mathematics & Optimization,
Vol. 72,
Issue. 3,
p.
523.
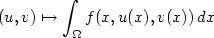 are obtained when sequences of fields v may develop oscillations and are
constrained to satisfy
a system of first order linear partial differential equations. This
framework includes the
treatement of divergence-free fields, Maxwell's equations in
micromagnetics, and curl-free
fields. In the latter case classical relaxation theorems in W1,p, are
recovered.
are obtained when sequences of fields v may develop oscillations and are
constrained to satisfy
a system of first order linear partial differential equations. This
framework includes the
treatement of divergence-free fields, Maxwell's equations in
micromagnetics, and curl-free
fields. In the latter case classical relaxation theorems in W1,p, are
recovered.


