Article contents
The internal stabilization by noise of the linearized Navier-Stokes equation*
Published online by Cambridge University Press: 30 October 2009
Abstract
One shows that the linearized Navier-Stokes equation in
${\mathcal{O}}{\subset} R^d,\;d \ge 2$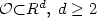 , around an unstable equilibrium
solution is exponentially stabilizable in probability by an
internal noise controller $V(t,\xi)=\displaystyle\sum\limits_{i=1}^{N} V_i(t)\psi_i(\xi)
\dot\beta_i(t)$
, around an unstable equilibrium
solution is exponentially stabilizable in probability by an
internal noise controller $V(t,\xi)=\displaystyle\sum\limits_{i=1}^{N} V_i(t)\psi_i(\xi)
\dot\beta_i(t)$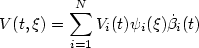 , $\xi\in{\mathcal{O}}$
, $\xi\in{\mathcal{O}}$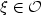 , where $\{\beta_i\}^N_{i=1}$
, where $\{\beta_i\}^N_{i=1}$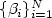 are
independent Brownian motions in a probability space and
$\{\psi_i\}^N_{i=1}$
are
independent Brownian motions in a probability space and
$\{\psi_i\}^N_{i=1}$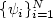 is a system of functions on ${\mathcal{O}}$
is a system of functions on ${\mathcal{O}}$ with
support in an arbitrary open subset ${\mathcal{O}}_0\subset {\mathcal{O}}$
with
support in an arbitrary open subset ${\mathcal{O}}_0\subset {\mathcal{O}}$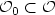 . The
stochastic control input $\{V_i\}^N_{i=1}$
. The
stochastic control input $\{V_i\}^N_{i=1}$ is found in feedback
form. One constructs also a tangential boundary noise controller
which exponentially stabilizes in probability the equilibrium
solution.
is found in feedback
form. One constructs also a tangential boundary noise controller
which exponentially stabilizes in probability the equilibrium
solution.
- Type
- Research Article
- Information
- ESAIM: Control, Optimisation and Calculus of Variations , Volume 17 , Issue 1 , January 2011 , pp. 117 - 130
- Copyright
- © EDP Sciences, SMAI, 2009
References
- 5
- Cited by


