Hostname: page-component-8448b6f56d-c47g7 Total loading time: 0 Render date: 2024-04-24T08:53:49.459Z Has data issue: false hasContentIssue false
  • English
  • Français

Weak ergodic averages over dilated measures

Part of: Ergodic theory

Published online by Cambridge University Press:  07 October 2019

WENBO SUN
WENBO SUN*
Affiliation:
Department of Mathematics, The Ohio State University, 231 West 18th Avenue, Columbus OH, 43210-1174, USA email sun.1991@osu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 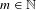$m\in \mathbb{N}$ and 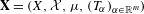$\mathbf{X}=(X,{\mathcal{X}},\unicode[STIX]{x1D707},(T_{\unicode[STIX]{x1D6FC}})_{\unicode[STIX]{x1D6FC}\in \mathbb{R}^{m}})$ be a measure-preserving system with an 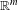$\mathbb{R}^{m}$-action. We say that a Borel measure $\unicode[STIX]{x1D708}$ on 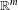$\mathbb{R}^{m}$ is weakly equidistributed for 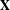$\mathbf{X}$ if there exists 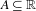$A\subseteq \mathbb{R}$ of density 1 such that, for all 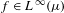$f\in L^{\infty }(\unicode[STIX]{x1D707})$, we have

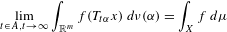$$\begin{eqnarray}\lim _{t\in A,t\rightarrow \infty }\int _{\mathbb{R}^{m}}f(T_{t\unicode[STIX]{x1D6FC}}x)\,d\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FC})=\int _{X}f\,d\unicode[STIX]{x1D707}\end{eqnarray}$$
for $\unicode[STIX]{x1D707}$-almost every 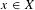$x\in X$. Let 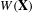$W(\mathbf{X})$ denote the collection of all $\unicode[STIX]{x1D6FC}\in \mathbb{R}^{m}$ such that the 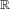$\mathbb{R}$-action 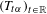$(T_{t\unicode[STIX]{x1D6FC}})_{t\in \mathbb{R}}$ is not ergodic. Under the assumption of the pointwise convergence of the double Birkhoff ergodic average, we show that a Borel measure $\unicode[STIX]{x1D708}$ on 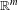$\mathbb{R}^{m}$ is weakly equidistributed for an ergodic system 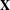$\mathbf{X}$ if and only if 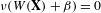$\unicode[STIX]{x1D708}(W(\mathbf{X})+\unicode[STIX]{x1D6FD})=0$ for every 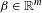$\unicode[STIX]{x1D6FD}\in \mathbb{R}^{m}$. Under the same assumption, we also show that $\unicode[STIX]{x1D708}$ is weakly equidistributed for all ergodic measure-preserving systems with 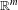$\mathbb{R}^{m}$-actions if and only if 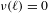$\unicode[STIX]{x1D708}(\ell )=0$ for all hyperplanes 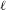$\ell$ of 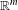$\mathbb{R}^{m}$. Unlike many equidistribution results in literature whose proofs use methods from harmonic analysis, our results adopt a purely ergodic-theoretic approach.

Keywords

ergodic theoryweak equidistributioncharacteristic factornilsystem

MSC classification

Primary: 37A05: Measure-preserving transformations
Secondary: 37A15: General groups of measure-preserving transformations 37A17: Homogeneous flows 37A25: Ergodicity, mixing, rates of mixing
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 41 , Issue 2 , February 2021 , pp. 606 - 621
Check for updates
Copyright
© Cambridge University Press, 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Assani, I.. Multiple recurrence and almost sure convergence for weakly mixing dynamical systems. Israel J. Math. 103 (1998), 111–124.CrossRefGoogle Scholar
Austin, T.. Norm convergence of continuous-time polynomial multiple ergodic averages. Ergod. Th. & Dynam. Sys. 32(2) (2012), 361–382.CrossRefGoogle Scholar
Bergelson, V. and Leibman, A.. Cubic averages and large intersections. Recent Trends in Ergodic Theory and Dynamical Systems (Contemporary Mathematics, 631) . American Mathematical Society, Providence, RI, 2015, pp. 5–19.Google Scholar
Bergelson, V., Leibman, A. and Moreira, J.. From discrete- to continuous-time ergodic theorems. Ergod. Th. & Dynam. Sys. 32(2) (2012), 383–426.CrossRefGoogle Scholar
Björklund, M.. Ergodic theorems for homogeneous dilations. Random Walks, Boundaries and Spectra (Progress in Probability, 64) . Eds. Lenz, D., Sobieczky, F. and Woess, W.. Springer, Basel, 2011.Google Scholar
Bourgain, J.. Double recurrence and almost sure convergence. J. Reine Angew. Math. 404 (1990), 140–161.Google Scholar
Chaika, J. and Hubert, P.. Circle averages and disjointness in typical flat surfaces on every Teichmüller disc. Bull. Lond. Math. Soc. 49(5) (2017), 755–769.CrossRefGoogle Scholar
Donoso, S. and Sun, W.. Pointwise convergence of some multiple ergodic averages. Adv. Math. 330 (2018), 946–996.CrossRefGoogle Scholar
Einsiedler, M. and Ward, T.. Ergodic Theory with a View towards Number Theory. Springer, London, 2011, 259.Google Scholar
Glasner, E.. Ergodic Theory via Joinings (Mathematical Surveys and Monographs, 101) . American Mathematical Society, Providence, RI, 2003.CrossRefGoogle Scholar
Gutman, Y., Huang, W., Shao, S. and Ye, X.. Almost sure convergence of the multiple ergodic average for certain weakly mixing systems. Acta Math. Sin. (Engl. Ser.) (1) 34 (2018), 79–90.CrossRefGoogle Scholar
Host, B.. Mixing of all orders and pairwise independent joining. Israel J. Math. 76 (1991), 289–298.CrossRefGoogle Scholar
Host, B.. Ergodic seminorms for commuting transformations and applications. Studia Math. 195 (2009), 31–49.10.4064/sm195-1-3CrossRefGoogle Scholar
Host, B. and Kra, B.. Nonconventional ergodic averages and nilmanifolds. Ann. of Math. (2) 161(1) (2005), 397–488.CrossRefGoogle Scholar
Huang, W., Shao, S. and Ye, X.. Pointwise convergence of multiple ergodic averages and strictly ergodic models. J. Anal. Math., to appear. Preprint, 2014, arXiv:1406.5930.Google Scholar
Jones, R. L.. Ergodic averages on spheres. J. Anal. Math. 61 (1993), 29–45.CrossRefGoogle Scholar
Kra, B., Shah, N. and Sun, W.. Equidistribution of dilated curves on nilmanifolds. J. Lond. Math. Soc. 98(3) (2018), 708–732.CrossRefGoogle Scholar
Lacey, M. T.. Ergodic averages on circles. J. Anal. Math. 67 (1995), 199–206.CrossRefGoogle Scholar
Leibman, A.. Pointwise convergence of ergodic averages for polynomial sequences of translations on a nilmanifold. Ergod. Th. & Dynam. Sys. 25(1) (2005), 201–213.10.1017/S0143385704000215CrossRefGoogle Scholar
Potts, A.. Multiple ergodic averages for flows and an application. Illinois J. Math. 55(2) (2011), 589–621.CrossRefGoogle Scholar
Pugh, C. and Shub, M.. Ergodic elements of ergodic actions. Compos. Math. 23 (1971), 115–122.Google Scholar
Shah, N. and Yang, P.. Stretching translates of shrinking curves and Dirichlet’s simultaneous approximation. Preprint, 2018, arXiv:1809.05570.Google Scholar
Stein, E. M.. Maximal functions: spherical means. Proc. Natl Acad. Sci. USA 73 (1976), 2174–2175.CrossRefGoogle ScholarPubMed
Ziegler, T.. Nilfactors of ℝ m -actions and configurations in sets of positive upper density in ℝ m . J. Anal. Math. 99 (2006), 249–266.CrossRefGoogle Scholar