Hostname: page-component-5c6d5d7d68-wbk2r Total loading time: 0 Render date: 2024-08-18T23:17:59.078Z Has data issue: false hasContentIssue false
  • English
  • Français

Weak colored local rules for planar tilings

Published online by Cambridge University Press:  05 April 2018

THOMAS FERNIQUE  and
MATHIEU SABLIK
THOMAS FERNIQUE
Affiliation:
Université Paris 13, CNRS, Sorbonne Paris Cité, UMR 7030, 93430 Villetaneuse, France email fernique@lipn.fr
MATHIEU SABLIK
Affiliation:
Institut de Mathématiques de Toulouse, UMR 5219, Université. de Toulouse, CNRS, Université P. Sabatier, France email mathieu.sablik@math.univ-toulouse.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

A linear subspace 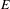$E$ of 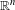$\mathbb{R}^{n}$ has colored local rules if there exists a finite set of decorated tiles whose tilings are digitizations of 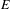$E$. The local rules are weak if the digitizations can slightly wander around 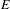$E$. We prove that a linear subspace has weak colored local rules if and only if it is computable. This goes beyond previous results, all based on algebraic subspaces. We prove an analogous characterization for sets of linear subspaces, including the set of all the linear subspaces of 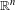$\mathbb{R}^{n}$.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 12 , December 2019 , pp. 3322 - 3346
Copyright
© Cambridge University Press, 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ammann, R., Grünbaum, B. and Shephard, G. C.. Aperiodic tiles. Discrete Comput. Geom. 8 (1992), 1–25.Google Scholar
Aubrun, N. and Sablik, M.. Simulation of effective subshifts by two-dimensional subshifts of finite type. Acta Appl. Math. 126 (2013), 35–63.Google Scholar
Beenker, F. P. M.. Algebric theory of non periodic tilings of the plane by two simple building blocks: a square and a rhombus. Technical Report TH Report 82-WSK-04. Technische Hogeschool Eindhoven, 1982.Google Scholar
Berger, R.. The Undecidability of the Domino Problem (Memoirs of the American Mathematical Society, 66) . American Mathematical Society, Providence, RI, 1966.Google Scholar
Bédaride, N. and Fernique, Th.. Weak local rules for planar octagonal tilings. Israel J. Math. 222 (2017), 63–89.Google Scholar
Bédaride, N. and Fernique, Th.. The Ammann–Beenker tilings revisited. Aperiodic Crystals. Springer, Dordrecht, 2013, pp. 59–65.Google Scholar
Bédaride, N. and Fernique, Th.. No weak local rules for the 4p-fold tilings. Discrete Comput. Geom. 54 (2015), 980–992.Google Scholar
Bédaride, N. and Fernique, Th.. When periodicities enforce aperiodicity. Commun. Math. Phys. 335 (2015), 1099–1120.Google Scholar
Baake, M. and Grimm, U.. Aperiodic Order (Encyclopedia of Mathematics and its Applications, 149) . Cambridge University Press, Cambridge, 2013.Google Scholar
Burkov, S. E.. Absence of weak local rules for the planar quasicrystalline tiling with the 8-fold rotational symmetry. Commun. Math. Phys. 119 (1988), 667–675.Google Scholar
De Bruijn, N. G.. Algebraic theory of Penrose’s nonperiodic tilings of the plane. Nederl. Akad. Wetensch. Indag. Math. 43 (1981), 39–52.Google Scholar
De Bruijn, N.. Dualization of multigrids. J. de Physique Colloques 47 (1986), 9–18.Google Scholar
Durand, B., Romashchenko, A. and Shen, A.. Fixed-point tile sets and their applications. J. Comput. Syst. Sci. 78 (2012), 731–764.Google Scholar
Dworkin, S. and Shieh, J.-I.. Deceptions in quasicrystal growth. Commun. Math. Phys. 168 (1995), 337–352.Google Scholar
Fernique, Th. and Ollinger, N.. Combinatorial substitutions and sofic tilings. Proceedings of JAC (TUCS Lecture Notes, 13) . Ed. Kari, J.. Turku Centre for Computer Science, Turku, 2010, pp. 100–110.Google Scholar
Gérard, Y., Debled-Rennesson, I. and Zimmermann, P.. An elementary digital plane recognition algorithm. Discrete Appl. Math. 151 (2005), 169–183.Google Scholar
Gähler, F. and Rhyner, J.. Equivalence of the generalised grid and projection methods for the construction of quasiperiodic tilings. J. Phys. A: Math. Gen. 19 (1986), 267–277.Google Scholar
Goodman-Strauss, Ch.. Matching rules and substitution tilings. Ann. Math. 147 (1998), 181–223.Google Scholar
Henley, Ch.. Random tiling models. Quasicrystals: The State of the Art. Eds. Steinhardt, P. J. and DiVincenzo, D. P.. World Scientific, Singapore, 1991, pp. 429–524.Google Scholar
Hochman, M. and Meyerovich, T.. A characterization of the entropies of multidimensional shifts of finite type. Ann. Math. 171 (2010), 2011–2038.Google Scholar
Hochman, M.. On the dynamics and recursive properties of multidimensional symbolic systems. Invent. Math. 176 (2009), 131–167.Google Scholar
Katz, A.. Theory of matching rules for the 3-dimensional Penrose tilings. Commun. Math. Phys. 118 (1988), 263–288.Google Scholar
Katz, A.. Matching rules and quasiperiodicity: the octagonal tilings. Beyond Quasicrystals: Les Houches, March 7–18, 1994. Springer, Berlin, 1995, pp. 141–189.Google Scholar
Kenyon, R.. Rigidity of planar tilings. Invent. Math. 107 (1992), 637–651.Google Scholar
Klette, R. and Rosenfeld, A.. Digital straightness—a review. Discrete Appl. Math. 139 (2003), 197–230.Google Scholar
Le, T. Q. T.. Local rules for pentagonal quasi-crystals. Discrete Comput. Geom. 14 (1995), 31–70.Google Scholar
Le, T. Q. T.. Local rules for quasiperiodic tilings. The Mathematics of Long-Range Aperiodic Order (Waterloo, ON, 1995) (NATO Adv. Sci. Inst. Ser. C Math. Phys. Sci., 489) . Kluwer Academic, Dordrecht, 1997, pp. 331–366.Google Scholar
Levitov, L. S.. Local rules for quasicrystals. Commun. Math. Phys. 119 (1988), 627–666.Google Scholar
Lothaire, M.. Algebraic Combinatorics on Words (Encyclopedia of Mathematics and its Applications, 90) . Cambridge University Press, Cambridge, 2002.Google Scholar
Le, T. Q. T. and Piunikhin, S.. Local rules for multi-dimensional quasicrystals. Differential Geom. Appl. 5 (1995), 10–31.Google Scholar
Le, T. Q. T., Piunikhin, S. and Sadov, V.. Local rules for quasiperiodic tilings of quadratic 2-planes in R 4 . Commun. Math. Phys. 150 (1992), 23–44.Google Scholar
Levine, D. and Steinhardt, P. J.. Quasicrystals: a new class of ordered structures. Phys. Rev. Lett. 53 (1984), 2477–2480.Google Scholar
Mignosi, F.. On the number of factors of sturmian words. Theor. Comput. Sci. 82 (1991), 71–84.Google Scholar
Mozes, S.. Tilings, substitution systems and dynamical systems generated by them. J. Anal. Math. 53 (1989), 139–186.Google Scholar
Penrose, R.. The rôle of aesthetics in pure and applied mathematical research. Inst. Math. Appl. Bull. 10 (1974), 266–271.Google Scholar
Penrose, R.. Pentaplexity: a class of non-periodic tilings of the plane. Eureka 39 (1978).Google Scholar
Pavlovitch, A. and Kleman, M.. Generalised 2d Penrose tilings: structural properties. J. Phys. A: Math. Gen. 20 (1987), 687–702.Google Scholar
Robinson, R. M.. Undecidability and nonperiodicity for tilings of the plane. Invent. Math. 12 (1971), 177–209.Google Scholar
Robinson, E. A.. Symbolic dynamics and tilings of ℝ d . Symbolic Dynamics Appl. 60 (2004), 81–119.Google Scholar
Sadun, L.. Topology of Tiling Spaces (University Lecture Series) . American Mathematical Society, Providence, RI, 2008.Google Scholar
Shechtman, D., Blech, I., Gratias, D. and Cahn, J. W.. Metallic phase with long-range orientational symmetry and no translational symmetry. Phys. Rev. Lett. 53 (1984), 1951–1953.Google Scholar
Senechal, M.. Quasicrystals and Geometry. Cambridge University Press, 1995.Google Scholar
Senechal, M.. The mysterious Mr. Ammann. Math. Intelligencer 26 (2008), 10–21.Google Scholar
Socolar, J. E. S.. Simple octagonal and dodecagonal quasicrystals. Phys. Rev. B 39 (1989), 519–551.Google Scholar
Socolar, J. E. S.. Weak matching rules for quasicrystals. Commun. Math. Phys. 129 (1990), 599–619.Google Scholar
Wang, H.. Proving theorems by pattern recognition I. Commun. ACM 3 (1960), 220–234.Google Scholar
Weihrauch, K.. Computable Analysis: An Introduction. Springer, Berlin, 2000.Google Scholar