Hostname: page-component-8448b6f56d-qsmjn Total loading time: 0 Render date: 2024-04-24T01:55:37.378Z Has data issue: false hasContentIssue false
  • English
  • Français

The weak Bernoulli property for matrix Gibbs states

Part of: Ergodic theory

Published online by Cambridge University Press:  18 December 2018

MARK PIRAINO Open the ORCID record for MARK PIRAINO [Opens in a new window]
MARK PIRAINO*
Affiliation:
Department of Mathematics and Statistics, University of Victoria, Canada email mpiraino@uvic.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the ergodic properties of a class of measures on 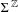$\unicode[STIX]{x1D6F4}^{\mathbb{Z}}$ for which 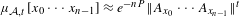$\unicode[STIX]{x1D707}_{{\mathcal{A}},t}[x_{0}\cdots x_{n-1}]\approx e^{-nP}\Vert A_{x_{0}}\cdots A_{x_{n-1}}\Vert ^{t}$, where ${\mathcal{A}}=(A_{0},\ldots ,A_{M-1})$ is a collection of matrices. The measure $\unicode[STIX]{x1D707}_{{\mathcal{A}},t}$ is called a matrix Gibbs state. In particular, we give a sufficient condition for a matrix Gibbs state to have the weak Bernoulli property. We employ a number of techniques to understand these measures, including a novel approach based on Perron–Frobenius theory. We find that when $t$ is an even integer the ergodic properties of 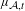$\unicode[STIX]{x1D707}_{{\mathcal{A}},t}$ are readily deduced from finite-dimensional Perron–Frobenius theory. We then consider an extension of this method to $t>0$ using operators on an infinite- dimensional space. Finally, we use a general result of Bradley to prove the main theorem.

Keywords

symbolic dynamicsthermodynamic formalismweak Bernoulli propertymatrix equilibrium states

MSC classification

Primary: 37A25: Ergodicity, mixing, rates of mixing
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 8 , August 2020 , pp. 2219 - 2238
Check for updates
Copyright
© Cambridge University Press, 2018

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bochi, J. and Morris, I. D.. Equilibrium states of generalised singular value potentials and applications to affine iterated function systems. Geom. Funct. Anal. 28(4) (2018), 995–1028.CrossRefGoogle Scholar
Bowen, R.. Bernoulli equilibrium states for Axiom A diffeomorphisms. Math. Syst. Theory 8(4) (1974/75), 289–294.CrossRefGoogle Scholar
Bowen, R.. Equilibrium States and the Ergodic Theory of Anosov Diffeomorphisms (Lecture Notes in Mathematics, 470), Revised edn. Ed. Chazottes, J.-R.. Springer, Berlin, 2008, with a preface by David Ruelle.CrossRefGoogle Scholar
Boyle, M. and Petersen, K.. Hidden Markov processes in the context of symbolic dynamics. Entropy of Hidden Markov Processes and Connections to Dynamical Systems (London Mathematical Society Lecture Note Series, 385). Cambridge University Press, Cambridge, 2011, pp. 5–71.CrossRefGoogle Scholar
Bradley, R. C.. Basic properties of strong mixing conditions. A survey and some open questions. Probab. Surv. 2 (2005), 107–144. Update of, and a supplement to, the 1986 original.CrossRefGoogle Scholar
Bradley, R. C. Jr. On the 𝜓-mixing condition for stationary random sequences. Trans. Amer. Math. Soc. 276(1) (1983), 55–66.Google Scholar
Cao, Y.-L., Feng, D.-J. and Huang, W.. The thermodynamic formalism for sub-additive potentials. Discrete Contin. Dyn. Syst. 20(3) (2008), 639–657.CrossRefGoogle Scholar
Chazottes, J.-R. and Ugalde, E.. Projection of Markov measures may be Gibbsian. J. Stat. Phys. 111(5–6) (2003), 1245–1272.CrossRefGoogle Scholar
Eveson, S. P. and Nussbaum, R. D.. Applications of the Birkhoff–Hopf theorem to the spectral theory of positive linear operators. Math. Proc. Cambridge Philos. Soc. 117(3) (1995), 491–512.CrossRefGoogle Scholar
Falconer, K. J.. The Hausdorff dimension of self-affine fractals. Math. Proc. Cambridge Philos. Soc. 103(2) (1988), 339–350.CrossRefGoogle Scholar
Feng, D.-J.. The limited Rademacher functions and Bernoulli convolutions associated with Pisot numbers. Adv. Math. 195(1) (2005), 24–101.CrossRefGoogle Scholar
Feng, D.-J.. Equilibrium states for factor maps between subshifts. Adv. Math. 226(3) (2011), 2470–2502.CrossRefGoogle Scholar
Feng, D.-J. and Käenmäki, A.. Equilibrium states of the pressure function for products of matrices. Discrete Contin. Dyn. Syst. 30(3) (2011), 699–708.CrossRefGoogle Scholar
Feng, D.-J. and Lau, K.-S.. The pressure function for products of non-negative matrices. Math. Res. Lett. 9(2–3) (2002), 363–378.CrossRefGoogle Scholar
Friedman, N. A. and Ornstein, D. S.. On isomorphism of weak Bernoulli transformations. Adv. Math. 5(1970) (1970), 365–394.CrossRefGoogle Scholar
Guivarc’h, Y. and Le Page, E.. Simplicité de spectres de Lyapounov et propriété d’isolation spectrale pour une famille d’opérateurs de transfert sur l’espace projectif. Random Walks and Geometry. Walter de Gruyter, Berlin, 2004, pp. 181–259.Google Scholar
Horn, R. A. and Johnson, C. R.. Matrix Analysis, 2nd edn. Cambridge University Press, Cambridge, 2013.Google Scholar
Johansson, A., Öberg, A. and Pollicott, M.. Ergodic theory of Kusuoka measures. J. Fract. Geom. 4(2) (2017), 185–214.CrossRefGoogle Scholar
Kusuoka, S.. Dirichlet forms on fractals and products of random matrices. Publ. Res. Inst. Math. Sci. 25(4) (1989), 659–680.CrossRefGoogle Scholar
Morris, I. D.. Ergodic properties of matrix equilibrium states. Ergod. Th. & Dynam. Sys. 38(6) (2018), 2295–2320.CrossRefGoogle Scholar
Morris, I. D.. A necessary and sufficient condition for a matrix equilibrium state to be mixing. Ergod. Th. & Dynam. Sys., to appear.Google Scholar
Ornstein, D. S.. Bernoulli shifts with the same entropy are isomorphic. Adv. Math. 4 (1970), 337–352.CrossRefGoogle Scholar
Ornstein, D. S.. On the root problem in ergodic theory. Proceedings of the Sixth Berkeley Symposium on Mathematical Statistics and Probability, Vol. II: Probability Theory. Eds. LeCam, L. M., Neyman, J. and Scott, E. L.. University of California Press, Berkeley, CA, 1972, pp. 347–356.Google Scholar
Piraino, M.. Projections of Gibbs states for Hölder potentials. J. Stat. Phys. 170(5) (2018), 952–961.CrossRefGoogle Scholar
Vandergraft, J. S.. Spectral properties of matrices which have invariant cones. SIAM J. Appl. Math. 16 (1968), 1208–1222.CrossRefGoogle Scholar
Walters, P.. Regularity conditions and Bernoulli properties of equilibrium states and g-measures. J. Lond. Math. Soc. (2) 71(2) (2005), 379–396.CrossRefGoogle Scholar
Yoo, J.. On factor maps that send Markov measures to Gibbs measures. J. Stat. Phys. 141(6) (2010), 1055–1070.CrossRefGoogle Scholar