Article contents
Surjunctivity and topological rigidity of algebraic dynamical systems
Published online by Cambridge University Press: 20 June 2017
Abstract
Let 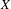 $X$ be a compact metrizable group and let
$X$ be a compact metrizable group and let  $\unicode[STIX]{x1D6E4}$ be a countable group acting on
$\unicode[STIX]{x1D6E4}$ be a countable group acting on 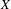 $X$ by continuous group automorphisms. We give sufficient conditions under which the dynamical system
$X$ by continuous group automorphisms. We give sufficient conditions under which the dynamical system 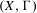 $(X,\unicode[STIX]{x1D6E4})$ is surjunctive, i.e. every injective continuous map
$(X,\unicode[STIX]{x1D6E4})$ is surjunctive, i.e. every injective continuous map 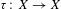 $\unicode[STIX]{x1D70F}:X\rightarrow X$ commuting with the action of
$\unicode[STIX]{x1D70F}:X\rightarrow X$ commuting with the action of 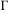 $\unicode[STIX]{x1D6E4}$ is surjective.
$\unicode[STIX]{x1D6E4}$ is surjective.
- Type
- Original Article
- Information
- Copyright
- © Cambridge University Press, 2017
References
- 3
- Cited by


