Article contents
A spectral refinement of the Bergelson–Host–Kra decomposition and new multiple ergodic theorems
Published online by Cambridge University Press: 07 September 2017
Abstract
We investigate how spectral properties of a measure-preserving system  $(X,{\mathcal{B}},\unicode[STIX]{x1D707},T)$ are reflected in the multiple ergodic averages arising from that system. For certain sequences
$(X,{\mathcal{B}},\unicode[STIX]{x1D707},T)$ are reflected in the multiple ergodic averages arising from that system. For certain sequences 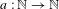 $a:\mathbb{N}\rightarrow \mathbb{N}$, we provide natural conditions on the spectrum
$a:\mathbb{N}\rightarrow \mathbb{N}$, we provide natural conditions on the spectrum 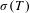 $\unicode[STIX]{x1D70E}(T)$ such that, for all
$\unicode[STIX]{x1D70E}(T)$ such that, for all 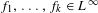 $f_{1},\ldots ,f_{k}\in L^{\infty }$,
$f_{1},\ldots ,f_{k}\in L^{\infty }$, 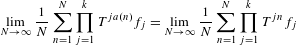 $$\begin{eqnarray}\lim _{N\rightarrow \infty }\frac{1}{N}\mathop{\sum }_{n=1}^{N}\mathop{\prod }_{j=1}^{k}T^{ja(n)}f_{j}=\lim _{N\rightarrow \infty }\frac{1}{N}\mathop{\sum }_{n=1}^{N}\mathop{\prod }_{j=1}^{k}T^{jn}f_{j}\end{eqnarray}$$
$$\begin{eqnarray}\lim _{N\rightarrow \infty }\frac{1}{N}\mathop{\sum }_{n=1}^{N}\mathop{\prod }_{j=1}^{k}T^{ja(n)}f_{j}=\lim _{N\rightarrow \infty }\frac{1}{N}\mathop{\sum }_{n=1}^{N}\mathop{\prod }_{j=1}^{k}T^{jn}f_{j}\end{eqnarray}$$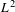 $L^{2}$-norm. In particular, our results apply to infinite arithmetic progressions,
$L^{2}$-norm. In particular, our results apply to infinite arithmetic progressions,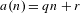 $a(n)=qn+r$, Beatty sequences,
$a(n)=qn+r$, Beatty sequences, 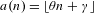 $a(n)=\lfloor \unicode[STIX]{x1D703}n+\unicode[STIX]{x1D6FE}\rfloor$, the sequence of squarefree numbers,
$a(n)=\lfloor \unicode[STIX]{x1D703}n+\unicode[STIX]{x1D6FE}\rfloor$, the sequence of squarefree numbers, 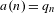 $a(n)=q_{n}$, and the sequence of prime numbers,
$a(n)=q_{n}$, and the sequence of prime numbers, 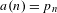 $a(n)=p_{n}$. We also obtain a new refinement of Szemerédi’s theorem via Furstenberg’s correspondence principle.
$a(n)=p_{n}$. We also obtain a new refinement of Szemerédi’s theorem via Furstenberg’s correspondence principle.
- Type
- Original Article
- Information
- Copyright
- © Cambridge University Press, 2017
References
A correction has been issued for this article:
- 7
- Cited by
Linked content
Please note a has been issued for this article.


