Hostname: page-component-8448b6f56d-t5pn6 Total loading time: 0 Render date: 2024-04-19T14:38:58.552Z Has data issue: false hasContentIssue false
  • English
  • Français

Quasi-shadowing for partially hyperbolic diffeomorphisms

Published online by Cambridge University Press:  15 December 2014

HUYI HU ,
YUNHUA ZHOU  and
YUJUN ZHU
HUYI HU
Affiliation:
Department of Mathematics, Michigan State University, East Lansing, MI 48824, USA email hhu@math.msu.edu
YUNHUA ZHOU
Affiliation:
College of Mathematics and Statistics, Chongqing University, Chongqing 401331, China email zhouyh@cqu.edu.cn
YUJUN ZHU
Affiliation:
College of Mathematics and Information Science, Hebei Normal University, Shijiazhuang 050024, China email yjzhu@mail.hebtu.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

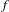A partially hyperbolic diffeomorphism $f$ has the quasi-shadowing property if for any pseudo orbit 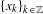$\{x_{k}\}_{k\in \mathbb{Z}}$, there is a sequence of points 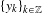$\{y_{k}\}_{k\in \mathbb{Z}}$ tracing it in which 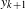$y_{k+1}$ is obtained from 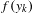$f(y_{k})$ by a motion ${\it\tau}$ along the center direction. We show that any partially hyperbolic diffeomorphism has the quasi-shadowing property, and if 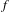$f$ has a 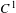$C^{1}$ center foliation then we can require ${\it\tau}$ to move the points along the center foliation. As applications, we show that any partially hyperbolic diffeomorphism is topologically quasi-stable under 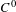$C^{0}$-perturbation. When 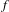$f$ has a uniformly compact $C^{1}$ center foliation, we also give partially hyperbolic diffeomorphism versions of some theorems which hold for uniformly hyperbolic systems, such as the Anosov closing lemma, the cloud lemma and the spectral decomposition theorem.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 35 , Issue 2 , April 2015 , pp. 412 - 430
Copyright
© Cambridge University Press, 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barreira, L. and Pesin, Y.. Non-uniform Hyperbolicity. Cambridge University Press, Cambridge, 2007.Google Scholar
Bohnet, D.. Codimension-1 partially hyperbolic diffeomorphisms with a uniformly compact center foliation. J. Mod. Dyn. 7 (2013), 565–604.Google Scholar
Bonatti, C. and Bohnet, D.. Partially hyperbolic diffeomorphisms with uniformly compact center foliations: the quotient dynamics, Preprint, 2014, arXiv:1210.2835.Google Scholar
Bonatti, C., Diaz, L. and Viana, M.. Dynamics Beyond Uniform Hyperbolicity: A Global Geometric and Probabilistic Perspective (Encyclopaedia of Mathematical Sciences, 102). Springer, Berlin, 2005.Google Scholar
Bowen, R.. Equilibrium States and the Ergodic Theory of Anosov Diffeomorphisms (Lecture Notes in Mathematics, 470). Springer, New York, 1975.Google Scholar
Brin, M. and Pesin, Y.. Partially hyperbolic dynamical systems. Math. USSR-Izv. 8 (1974), 177–218.Google Scholar
Carrasco, P.. Compact dynamical foliations. PhD Thesis, University of Toronto, 2011.Google Scholar
Hirsch, M., Pugh, C. and Shub, M.. Invariant Manifolds (Lecture Notes in Mathematics, 583). Springer, New York, 1977.CrossRefGoogle Scholar
Hu, H. and Zhu, Y.. Quasi-stability for partially hyperbolic diffeomorphisms. Trans. Amer. Math. Soc. 366 (2014), 3787–3804.Google Scholar
Katok, A. and Hasselblatt, B.. Introduction to the Modern Theory of Dynamical Systems. Cambridge University Press, Cambridge, 1995.Google Scholar
Kryzhevich, S. and Tikhomirov, S.. Partial hyperbolicity and central shadowing. Discrete Contin. Dyn. Syst. 33 (2013), 2901–2909.Google Scholar
Pesin, Y.. Lectures on Partial Hyperbolicity and Stable Ergodicity (Zurich Lectures in Advanced Mathematics). European Mathematical Society, Zurich, 2004.Google Scholar
Pilyugin, S. Yu.. Shadowing in Dynamical Systems (Lecture Notes in Mathematics, 1706). Springer, New York, 1999.Google Scholar
Pugh, C. and Shub, M.. Stably ergodic dynamical systems and partial hyperbolicity. J. Complexity 13 (1997), 125–179.Google Scholar
Shub, M.. Global Stability of Dynamical Systems. Springer, New York, 1987.Google Scholar
Walters, P.. Anosov diffeomorphisms are topologically stable. Topology 9 (1970), 71–78.Google Scholar
Walters, P.. On the Pseudo-Orbit Tracing Property and its Relationship to Stability (Lecture Notes in Mathematics, 668). Springer, New York, 1978, pp. 231–244.Google Scholar