Hostname: page-component-76fb5796d-2lccl Total loading time: 0 Render date: 2024-04-25T12:13:35.336Z Has data issue: false hasContentIssue false
  • English
  • Français

Purely exponential growth of cusp-uniform actions

Published online by Cambridge University Press:  20 June 2017

WEN-YUAN YANG
WEN-YUAN YANG*
Affiliation:
Beijing International Center for Mathematical Research and School of Mathematical Sciences, Peking University, Beijing, 100871, PR China email yabziz@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Suppose that a countable group 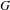$G$ admits a cusp-uniform action on a hyperbolic space 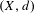$(X,d)$ such that $G$ is of divergent type. The main result of the paper is characterizing the purely exponential growth type of the orbit growth function by a condition introduced by Dal’bo, Otal and Peigné [Séries de Poincaré des groupes géométriquement finis. Israel J. Math.118(3) (2000), 109–124]. For geometrically finite Cartan–Hadamard manifolds with pinched negative curvature, this condition ensures the finiteness of Bowen–Margulis–Sullivan measures. In this case, our result recovers a theorem of Roblin (in a coarse form). Our main tool is the Patterson–Sullivan measures on the Gromov boundary of $X$, and a variant of the Sullivan shadow lemma called the partial shadow lemma. This allows us to prove that the purely exponential growth of either cones, or partial cones or horoballs is also equivalent to the Dal’bo–Otal–Peigné condition. These results are used further in a paper by the present author [W. Yang, Patterson–Sullivan measures and growth of relatively hyperbolic groups. Preprint, 2013, arXiv:1308.6326].

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 3 , March 2019 , pp. 795 - 831
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arzhantseva, G. and Lysenok, I.. Growth tightness for word hyperbolic groups. Math. Z. 241(3) (2002), 597–611.Google Scholar
Bowditch, B.. Convergence groups and configuration spaces. Geometric Group Theory Down Under: Proceedings of a Special Year in Geometric Group Theory, Canberra, Australia. Eds. Cossey, J., Miller, C. F., Neumann, W. D. and Shapiro, M.. de Gruyter, Berlin, 1999, pp. 23–54.Google Scholar
Bowditch, B.. Relatively hyperbolic groups. Internat. J. Algebra Comput. 22 (3) (2012), Paper No. 1250016.Google Scholar
Bridson, M. and Haefliger, A.. Metric Spaces of Non-positive Curvature (Grundlehren der Mathematischen Wissenschaften, 319) . Springer, Berlin, 1999.Google Scholar
Coornaert, M.. Mesures de Patterson–Sullivan sur le bord d’un espace hyperbolique au sens de Gromov. Pacific J. Math. 159(2) (1993), 241–270.Google Scholar
Dal’bo, F., Otal, P. and Peigné, M.. Séries de Poincaré des groupes géométriquement finis. Israel J. Math. 118(3) (2000), 109–124.Google Scholar
Drutu, C. and Sapir, M.. Tree-graded spaces and asymptotic cones of groups. Topology 44(5) (2005), 959–1058; with an appendix by D. Osin and M. Sapir.Google Scholar
Farb, B.. Relatively hyperbolic groups. Geom. Funct. Anal. 8(5) (1998), 810–840.Google Scholar
Gaboriau, D. and Paulin, F.. Sur les immeubles hyperboliques. Geom. Dedicata 88(1) (2001), 153–197.Google Scholar
Gerasimov, V.. Expansive convergence groups are relatively hyperbolic. Geom. Funct. Anal. 19(1) (2009), 137–169.Google Scholar
Ghys, E. and de la Harpe, P.. Sur les groupes hyperboliques d’après Mikhael Gromov (Progress in Mathematics) . Birkaüser, Basel, 1990.Google Scholar
Grigorchuk, R. and de la Harpe, P.. On problems related to growth, entropy and spectrum in group theory. J. Dyn. Control Syst. 3(1) (1997), 51–89.Google Scholar
Gromov, M.. Hyperbolic groups. Essays in Group Theory. Vol. 1. Ed. Gersten, S.. Springer, New York, 1987, pp. 75–263.Google Scholar
Hruska, G.. Relative hyperbolicity and relative quasiconvexity for countable groups. Algebr. Geom. Topol. 10(3) (2010), 1807–1856.Google Scholar
Marden, M.. The geometry of finitely generated Kleinian groups. Ann. of Math. (2) 99(3) (1974), 383–462.Google Scholar
Osin, D.. Elementary subgroups of relatively hyperbolic groups and bounded generation. Internat. J. Algebra Comput. 16(1) (2006), 99–118.Google Scholar
Osin, D.. Relatively hyperbolic groups: intrinsic geometry, algebraic properties, and algorithmic problems. Mem. Amer. Math. Soc. 179(843) (2006).Google Scholar
Patterson, S.. The limit set of a Fuchsian group. Acta Math. 136(1) (1976), 241–273.Google Scholar
Peigné, M.. On some exotic schottky groups. Discrete Contin. Dyn. Syst. 118(31) (2011), 559–579.Google Scholar
Roblin, T.. Ergodicité et équidistribution en courbure négative (Mémoires de la SMF, 95) . Société Matématique de France, Paris, 2003.Google Scholar
Sullivan, D.. The density at infinity of a discrete group of hyperbolic motions. Publ. Math. Inst. Hautes Études Sci. 50 (1979), 171–202.Google Scholar
Sullivan, D.. Entropy, Hausdorff measures old and new, and limit sets of geometrically finite Kleinian groups. Acta Math. 153 (1984), 259–277.Google Scholar
Tukia, P.. Conical limit points and uniform convergence groups. J. Reine Angew. Math. 501 (1998), 71–98.Google Scholar
Yaman, A.. A topological characterisation of relatively hyperbolic groups. J. Reine Angew. Math. 566 (2004), 41–89.Google Scholar
Yang, W.. Patterson–Sullivan measures and growth of relatively hyperbolic groups. Preprint, 2013,arXiv:1308.6326.Google Scholar
Yue, C.. The ergodic theory of discrete isometry groups on manifolds of variable negative curvature. Trans. Amer. Math. Soc. 48(12) (1996), 4965–5005.Google Scholar