Hostname: page-component-77c89778f8-fv566 Total loading time: 0 Render date: 2024-07-20T18:18:58.975Z Has data issue: false hasContentIssue false
  • English
  • Français

Poisson law for some non-uniformly hyperbolic dynamical systems with polynomial rate of mixing

Published online by Cambridge University Press:  10 August 2015

FRANÇOISE PÈNE  and
BENOÎT SAUSSOL
FRANÇOISE PÈNE
Affiliation:
Université de Brest, Laboratoire de Mathématiques de Bretagne Atlantique, CNRS UMR 6205, Brest, France email francoise.pene@univ-brest.fr, benoit.saussol@univ-brest.fr
BENOÎT SAUSSOL
Affiliation:
Université de Brest, Laboratoire de Mathématiques de Bretagne Atlantique, CNRS UMR 6205, Brest, France email francoise.pene@univ-brest.fr, benoit.saussol@univ-brest.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider some non-uniformly hyperbolic invertible dynamical systems which are modeled by a Gibbs–Markov–Young tower. We assume a polynomial tail for the inducing time and a polynomial control of hyperbolicity, as introduced by Alves, Pinheiro and Azevedo. These systems admit a physical measure with polynomial rate of mixing. 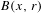In this paper we prove that the distribution of the number of visits to a ball $B(x,r)$ converges to a Poisson distribution as the radius 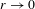$r\rightarrow 0$ and after suitable normalization.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 36 , Issue 8 , December 2016 , pp. 2602 - 2626
Copyright
© Cambridge University Press, 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alves, J. F. and Azevedo, D.. Statistical properties of diffeomorphisms with weak invariant manifolds. Discrete Contin. Dyn. Syst., to appear, 2013, arXiv:1310.2754.Google Scholar
Alves, J. F. and Pinheiro, V.. Slow rates of mixing for dynamical systems with hyperbolic structure. J. Stat. Phys. 131 (2008), 505–534.Google Scholar
Aytac, H., Freitas, J. M. and Vaienti, S.. Laws of rare events for deterministic and random dynamical systems. Trans. Amer. Math. Soc., to appear, 2012, doi:10.1090/S0002-9947-2014-06300-9.Google Scholar
Bálint, P. and Gouëzel, S.. Limit theorems in the stadium billiard. Comm. Math. Phys. 263(2) (2006), 461–512.Google Scholar
Barreira, L., Pesin, Ya. and Schmeling, J.. Dimension and product structure of hyperbolic measures. Ann. of Math. (2) 149(2) (1999), 755–783.CrossRefGoogle Scholar
Barreira, L. and Saussol, B.. Hausdorff dimension of measures via Poincaré recurrence. Comm. Math. Phys. 219 (2001), 443–464.Google Scholar
Billingsley, P.. Convergence of Probability Measures (Wiley Series in Probability and Statistics: Probability and Statistics) , 2nd edn. John Wiley, New York, 1999.Google Scholar
Chazottes, J.-R. and Collet, P.. Poisson approximation for the number of visits to balls in non-uniformly hyperbolic dynamical systems. Ergod. Th. & Dynam. Sys. 33(1) (2013), 49–80.Google Scholar
Chernov, N. and Markarian, R.. Chaotic Billiards (Mathematical Surveys and Monographs, 127) . American Mathematical Society, Providence, RI, 2006.CrossRefGoogle Scholar
Chernov, N. and Zhang, H.-K.. Billiards with polynomial mixing rates. Nonlinearity 18(4) (2005), 1527–1553.Google Scholar
Dedecker, J., Gouëzel, S. and Merlevède, F.. Some almost sure results for unbounded functions of intermittent maps and their associated Markov chains. Ann. Inst. Henri Poincaré Probab. Stat. 46(3) (2010), 796–821.Google Scholar
Fan, A. H.. Sur les dimensions de mesures. Studia Math. 111(1) (1994), 1–17.Google Scholar
Freitas, J., Haydn, N. and Nicol, M.. Convergence of rare events point processes to the Poisson for billiards. Nonlinearity 27(7) (2014), 1669–1687.CrossRefGoogle Scholar
Galatolo, S., Rousseau, J. and Saussol, B.. Skew products, quantitative recurrence, shrinking targets and decay of correlations. Ergod. Th. & Dynam. Sys., to appear. Published online 3 July 2014, doi:10.1017/etds.2014.10.Google Scholar
Haydn, N. and Wasilewska, K.. Limiting distribution and error terms for the number of visits to balls in non-uniformly hyperbolic dynamical systems. Preprint, 2014, arXiv:1402.2990.Google Scholar
Liverani, C., Saussol, B. and Vaienti, S.. A probabilistic approach to intermittency. Ergod. Th. & Dynam. Sys. 19 (1999), 671–685.Google Scholar
Markarian, R.. Billiards with polynomial decay of correlations. Ergod. Th. & Dynam. Sys. 24(1) (2004), 177–197.CrossRefGoogle Scholar
Rousseau, J. and Saussol, B.. Poincaré recurrence for observations. Trans. Amer. Math. Soc. 362(11) (2010), 5845–5859.CrossRefGoogle Scholar
Saussol, B.. Recurrence rate in rapidly mixing dynamical systems. Discrete Contin. Dyn. Syst. 15 (2006), 259–267.Google Scholar
Young, L.-S.. Statistical properties of dynamical systems with some hyperbolicity. Ann. of Math. (2) 147 (1998), 585–650.Google Scholar
Young, L.-S.. Recurrence times and rates of mixing. Israel J. Math. 110 (1999), 153–188.Google Scholar
Zweimüller, R.. The general asymptotic return-time process. Israel J. Math. to appear.Google Scholar