Article contents
On the 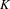 $K$-theory of
$K$-theory of 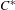 $C^{\ast }$-algebras arising from integral dynamics
$C^{\ast }$-algebras arising from integral dynamics
Published online by Cambridge University Press: 22 September 2016
Abstract
We investigate the 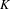 $K$-theory of unital UCT Kirchberg algebras
$K$-theory of unital UCT Kirchberg algebras 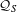 ${\mathcal{Q}}_{S}$ arising from families
${\mathcal{Q}}_{S}$ arising from families  $S$ of relatively prime numbers. It is shown that
$S$ of relatively prime numbers. It is shown that 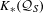 $K_{\ast }({\mathcal{Q}}_{S})$ is the direct sum of a free abelian group and a torsion group, each of which is realized by another distinct
$K_{\ast }({\mathcal{Q}}_{S})$ is the direct sum of a free abelian group and a torsion group, each of which is realized by another distinct 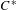 $C^{\ast }$-algebra naturally associated to
$C^{\ast }$-algebra naturally associated to  $S$. The
$S$. The 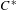 $C^{\ast }$-algebra representing the torsion part is identified with a natural subalgebra
$C^{\ast }$-algebra representing the torsion part is identified with a natural subalgebra 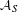 ${\mathcal{A}}_{S}$ of
${\mathcal{A}}_{S}$ of 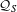 ${\mathcal{Q}}_{S}$. For the
${\mathcal{Q}}_{S}$. For the 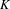 $K$-theory of
$K$-theory of 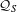 ${\mathcal{Q}}_{S}$, the cardinality of
${\mathcal{Q}}_{S}$, the cardinality of  $S$ determines the free part and is also relevant for the torsion part, for which the greatest common divisor
$S$ determines the free part and is also relevant for the torsion part, for which the greatest common divisor 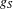 $g_{S}$ of
$g_{S}$ of 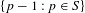 $\{p-1:p\in S\}$ plays a central role as well. In the case where
$\{p-1:p\in S\}$ plays a central role as well. In the case where 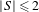 $|S|\leq 2$ or
$|S|\leq 2$ or 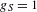 $g_{S}=1$ we obtain a complete classification for
$g_{S}=1$ we obtain a complete classification for 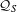 ${\mathcal{Q}}_{S}$. Our results support the conjecture that
${\mathcal{Q}}_{S}$. Our results support the conjecture that 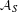 ${\mathcal{A}}_{S}$ coincides with
${\mathcal{A}}_{S}$ coincides with 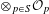 $\otimes _{p\in S}{\mathcal{O}}_{p}$. This would lead to a complete classification of
$\otimes _{p\in S}{\mathcal{O}}_{p}$. This would lead to a complete classification of 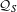 ${\mathcal{Q}}_{S}$, and is related to a conjecture about
${\mathcal{Q}}_{S}$, and is related to a conjecture about 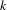 $k$-graphs.
$k$-graphs.
- Type
- Original Article
- Information
- Copyright
- © Cambridge University Press, 2016
References
- 6
- Cited by


