Published online by Cambridge University Press: 17 May 2021
We give an example of a principal algebraic action of the non-commutative free group 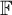 ${\mathbb {F}}$
of rank two by automorphisms of a connected compact abelian group for which there is an explicit measurable isomorphism with the full Bernoulli 3-shift action of
${\mathbb {F}}$
of rank two by automorphisms of a connected compact abelian group for which there is an explicit measurable isomorphism with the full Bernoulli 3-shift action of 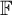 ${\mathbb {F}}$
. The isomorphism is defined using homoclinic points, a method that has been used to construct symbolic covers of algebraic actions. To our knowledge, this is the first example of a Bernoulli algebraic action of
${\mathbb {F}}$
. The isomorphism is defined using homoclinic points, a method that has been used to construct symbolic covers of algebraic actions. To our knowledge, this is the first example of a Bernoulli algebraic action of 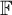 ${\mathbb {F}}$
without an obvious independent generator. Our methods can be generalized to a large class of acting groups.
${\mathbb {F}}$
without an obvious independent generator. Our methods can be generalized to a large class of acting groups.