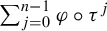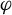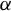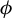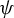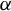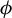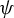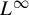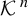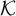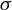1 Introduction and a preview of the main results
1.1 Quenched limit theorems for random dynamical systems
Let
![]() $(X,{\mathcal B},m)$
be a probability space and let
$(X,{\mathcal B},m)$
be a probability space and let
![]() $({\Omega },{\mathcal F},{\mathbb P},{\sigma })$
be an invertible ergodic probability-preserving system. Let
$({\Omega },{\mathcal F},{\mathbb P},{\sigma })$
be an invertible ergodic probability-preserving system. Let
![]() $T_{\omega }:X\to X,\,{\omega }\in {\Omega }$
, be a family of non-singular maps (that is,
$T_{\omega }:X\to X,\,{\omega }\in {\Omega }$
, be a family of non-singular maps (that is,
![]() ${m\circ T_\omega ^{-1}\ll m}$
) so that the corresponding skew product
${m\circ T_\omega ^{-1}\ll m}$
) so that the corresponding skew product
![]() $\tau $
given by
$\tau $
given by
![]() $\tau ({\omega },x)=({\sigma }{\omega },T_{\omega } x)$
is measurable. A random dynamical system is formed by the sequence of compositions
$\tau ({\omega },x)=({\sigma }{\omega },T_{\omega } x)$
is measurable. A random dynamical system is formed by the sequence of compositions
taken along the orbit of a ‘random’ point
![]() ${\omega }$
. The system
${\omega }$
. The system
![]() $({\Omega },{\mathcal F},{\mathbb P},{\sigma })$
is often referred to as the driving system, and the map
$({\Omega },{\mathcal F},{\mathbb P},{\sigma })$
is often referred to as the driving system, and the map
![]() ${\sigma }$
is often referred to as the base map.
${\sigma }$
is often referred to as the base map.
Let
![]() $\varphi :{\Omega }\times X\to {\mathbb R}$
be a measurable function (an ‘observable’) and let
$\varphi :{\Omega }\times X\to {\mathbb R}$
be a measurable function (an ‘observable’) and let
![]() $\mu $
be a
$\mu $
be a
![]() $\tau $
-invariant probability measure on
$\tau $
-invariant probability measure on
![]() ${\Omega }\times X$
. Then
${\Omega }\times X$
. Then
![]() $\mu $
can be decomposed as
$\mu $
can be decomposed as
![]() ${\mu =\int \mu _{\omega } \,d{\mathbb P}({\omega })}$
, where
${\mu =\int \mu _{\omega } \,d{\mathbb P}({\omega })}$
, where
![]() $\mu _{\omega }$
is a family of probability measures on X so that
$\mu _{\omega }$
is a family of probability measures on X so that
![]() ${(T_{\omega })_*\mu _{\omega }=\mu _{{\sigma }{\omega }}}$
for
${(T_{\omega })_*\mu _{\omega }=\mu _{{\sigma }{\omega }}}$
for
![]() ${\mathbb P}$
-almost every (a.e.)
${\mathbb P}$
-almost every (a.e.)
![]() ${\omega }$
. Set
${\omega }$
. Set
![]() $S_n\varphi =\sum _{j=0}^{n-1}\varphi \circ \tau ^j$
. Then
$S_n\varphi =\sum _{j=0}^{n-1}\varphi \circ \tau ^j$
. Then
 $$ \begin{align*}S_n\varphi({\omega},x):=S_n^{\omega}\varphi(x)=\sum_{j=0}^{n-1}\varphi_{\sigma^j{\omega}}\circ T_{\omega}^j,\end{align*} $$
$$ \begin{align*}S_n\varphi({\omega},x):=S_n^{\omega}\varphi(x)=\sum_{j=0}^{n-1}\varphi_{\sigma^j{\omega}}\circ T_{\omega}^j,\end{align*} $$
where
![]() $\varphi _{\omega }(\cdot )=\varphi ({\omega },\cdot )$
. For
$\varphi _{\omega }(\cdot )=\varphi ({\omega },\cdot )$
. For
![]() ${\mathbb P}$
-a.e.
${\mathbb P}$
-a.e.
![]() ${\omega }$
we can consider the sequence of functions
${\omega }$
we can consider the sequence of functions
![]() $S_n^{\omega }\varphi (\cdot )$
on the probability space
$S_n^{\omega }\varphi (\cdot )$
on the probability space
![]() $(X,{\mathcal B},\mu _{\omega })$
as random variables. Limit theorems for such sequences are called quenched limit theorems. Among the first papers dealing with quenched limit theorems for random dynamical systems are [Reference Kifer36, Reference Kifer37], where in [Reference Kifer36] a quenched large-deviations principle was obtained, and in [Reference Kifer37] a central limit theorem (CLT) and a law of the iterated logarithm were established. Since then quenched limit theorems for random dynamical systems have been extensively studied. For instance, in [Reference Dragičević, Froyland, González-Tokman and Vaienti16, Reference Dragičević, Hafouta, Pollicott and Vaienti20–Reference Dragičević, Hafouta and Sedro22] almost sure invariance principle (ASIP, an almost sure approximation by a sum of independent Gaussians) was established for random expanding or hyperbolic maps
$(X,{\mathcal B},\mu _{\omega })$
as random variables. Limit theorems for such sequences are called quenched limit theorems. Among the first papers dealing with quenched limit theorems for random dynamical systems are [Reference Kifer36, Reference Kifer37], where in [Reference Kifer36] a quenched large-deviations principle was obtained, and in [Reference Kifer37] a central limit theorem (CLT) and a law of the iterated logarithm were established. Since then quenched limit theorems for random dynamical systems have been extensively studied. For instance, in [Reference Dragičević, Froyland, González-Tokman and Vaienti16, Reference Dragičević, Hafouta, Pollicott and Vaienti20–Reference Dragičević, Hafouta and Sedro22] almost sure invariance principle (ASIP, an almost sure approximation by a sum of independent Gaussians) was established for random expanding or hyperbolic maps
![]() $T_{\omega }$
, in [Reference Dragičević and Hafouta19, Reference Hafouta and Kifer31] Berry–Esseen theorems (optimal rates in the CLT) were obtained for similar classes of maps and in [Reference Dragičević, Froyland, González-Tokman and Vaienti17, Reference Dragičević, Froyland, González-Tokman and Vaienti18, Reference Dragičević and Sedro23, Reference Hafouta and Kifer31] local CLTs were achieved. In addition, in [Reference Hafouta27] several limit theorems were extended to random non-uniformly hyperbolic or expanding maps. We would also like to refer to [Reference Alves, Bahsoun and Ruziboev3] for related results concerning mixing rates for random non-uniformly hyperbolic maps and to [Reference Haydn, Nicol, Török and Vaienti32] for related results concerning sequential dynamical systems, where an ASIP was obtained. We note that in many of the examples these results are obtained for the unique measure
$T_{\omega }$
, in [Reference Dragičević and Hafouta19, Reference Hafouta and Kifer31] Berry–Esseen theorems (optimal rates in the CLT) were obtained for similar classes of maps and in [Reference Dragičević, Froyland, González-Tokman and Vaienti17, Reference Dragičević, Froyland, González-Tokman and Vaienti18, Reference Dragičević and Sedro23, Reference Hafouta and Kifer31] local CLTs were achieved. In addition, in [Reference Hafouta27] several limit theorems were extended to random non-uniformly hyperbolic or expanding maps. We would also like to refer to [Reference Alves, Bahsoun and Ruziboev3] for related results concerning mixing rates for random non-uniformly hyperbolic maps and to [Reference Haydn, Nicol, Török and Vaienti32] for related results concerning sequential dynamical systems, where an ASIP was obtained. We note that in many of the examples these results are obtained for the unique measure
![]() $\mu $
such that
$\mu $
such that
![]() $\mu _{\omega }$
is absolutely continuous with respect to m. However, some results hold true even for maps
$\mu _{\omega }$
is absolutely continuous with respect to m. However, some results hold true even for maps
![]() $T_{\omega }:{\mathcal E}_{\omega }\to {\mathcal E}_{\sigma {\omega }}\subset X$
which are defined on random subsets of X (see [Reference Kifer, Lui, Hasselblatt and Katok40]), where in this case the most notable choices of
$T_{\omega }:{\mathcal E}_{\omega }\to {\mathcal E}_{\sigma {\omega }}\subset X$
which are defined on random subsets of X (see [Reference Kifer, Lui, Hasselblatt and Katok40]), where in this case the most notable choices of
![]() $\mu _{\omega }$
are the so-called random Gibbs measures (see [Reference Hafouta and Kifer31, Reference Mayer, Skorulski and Urbański44]).
$\mu _{\omega }$
are the so-called random Gibbs measures (see [Reference Hafouta and Kifer31, Reference Mayer, Skorulski and Urbański44]).
1.2 Limit theorem skew products
Let us consider the sums
![]() $S_n\varphi =\sum _{j=0}^{n-1}\varphi \circ \tau ^j$
as random variables on the probability space
$S_n\varphi =\sum _{j=0}^{n-1}\varphi \circ \tau ^j$
as random variables on the probability space
![]() $({\Omega }\times X,{\mathcal F}\times {\mathcal B},\mu )$
. In this paper will focus on limit theorems for such sequences of random variables. In order to demonstrate the difference between such limit theorems and the quenched ones, let us focus of the CLT. The quenched CLT means that for
$({\Omega }\times X,{\mathcal F}\times {\mathcal B},\mu )$
. In this paper will focus on limit theorems for such sequences of random variables. In order to demonstrate the difference between such limit theorems and the quenched ones, let us focus of the CLT. The quenched CLT means that for
![]() ${\mathbb P}$
-a.e.
${\mathbb P}$
-a.e.
![]() ${\omega }$
, for all real t, we have
${\omega }$
, for all real t, we have
 $$ \begin{align*} \lim_{n\to\infty}\mu_{\omega}(\{x: S_n^{\omega}\varphi(x)-\mu_{\omega}(S_n^{\omega}\varphi)\leq t\sqrt n\})= \frac{1}{\sqrt{2\pi}{\sigma}}\int_{-\infty}^{t}e^{-{s^2}/{2{\sigma}^2}}ds \end{align*} $$
$$ \begin{align*} \lim_{n\to\infty}\mu_{\omega}(\{x: S_n^{\omega}\varphi(x)-\mu_{\omega}(S_n^{\omega}\varphi)\leq t\sqrt n\})= \frac{1}{\sqrt{2\pi}{\sigma}}\int_{-\infty}^{t}e^{-{s^2}/{2{\sigma}^2}}ds \end{align*} $$
where
![]() ${\sigma }\geq 0$
is the number that satisfies
${\sigma }\geq 0$
is the number that satisfies
![]() ${\sigma }^2=\lim _{n\to \infty }(1/n)\mathrm {Var}_{\mu _{\omega }}(S_n^{\omega }\varphi )$
for
${\sigma }^2=\lim _{n\to \infty }(1/n)\mathrm {Var}_{\mu _{\omega }}(S_n^{\omega }\varphi )$
for
![]() ${\mathbb P}$
-a.e.
${\mathbb P}$
-a.e.
![]() ${\omega }$
(assuming that this limit exists and does not depend on
${\omega }$
(assuming that this limit exists and does not depend on
![]() ${\omega }$
, refer to [Reference Kifer37, Theorem 2.3] for sufficient conditions). On the other hand, the CLT for the skew product means that for all real t we have
${\omega }$
, refer to [Reference Kifer37, Theorem 2.3] for sufficient conditions). On the other hand, the CLT for the skew product means that for all real t we have
 $$ \begin{align*} \lim_{n\to\infty}\mu(\{({\omega},x): S_n\varphi({\omega},x)-\mu(S_n\varphi)\leq t\sqrt n\})= \frac{1}{\sqrt{2\pi}{\Sigma}}\int_{-\infty}^{t}e^{-{s^2}/{2{\Sigma}^2}}ds, \end{align*} $$
$$ \begin{align*} \lim_{n\to\infty}\mu(\{({\omega},x): S_n\varphi({\omega},x)-\mu(S_n\varphi)\leq t\sqrt n\})= \frac{1}{\sqrt{2\pi}{\Sigma}}\int_{-\infty}^{t}e^{-{s^2}/{2{\Sigma}^2}}ds, \end{align*} $$
where
![]() ${\Sigma }^2=\lim _{n\to \infty }(1/n)\mathrm {Var}_{\mu }(S_n\varphi )$
. Note that, in contrast to the quenched case, the summands
${\Sigma }^2=\lim _{n\to \infty }(1/n)\mathrm {Var}_{\mu }(S_n\varphi )$
. Note that, in contrast to the quenched case, the summands
![]() $X_j=\varphi \circ \tau ^j$
form a stationary sequence and, in applications, the existence of the limit
$X_j=\varphi \circ \tau ^j$
form a stationary sequence and, in applications, the existence of the limit
![]() ${\Sigma }^2$
follows from a sufficiently fast decay of
${\Sigma }^2$
follows from a sufficiently fast decay of
![]() $\mathrm {Cov}(X_0,X_n)$
as
$\mathrm {Cov}(X_0,X_n)$
as
![]() $n\to \infty $
. We also remark that both CLT’s above are formulated when
$n\to \infty $
. We also remark that both CLT’s above are formulated when
![]() ${\sigma }$
and
${\sigma }$
and
![]() ${\Sigma }$
are positive, and when one of them vanishes the convergence is towards the constant function
${\Sigma }$
are positive, and when one of them vanishes the convergence is towards the constant function
![]() $0$
.
$0$
.
When
![]() $\mu _{\omega }(\varphi _{\omega })$
does not depend on
$\mu _{\omega }(\varphi _{\omega })$
does not depend on
![]() ${\omega }$
, we have that
${\omega }$
, we have that
![]() $\mu _{\omega }(\varphi _{\omega })=\mu (\varphi )$
and
$\mu _{\omega }(\varphi _{\omega })=\mu (\varphi )$
and
![]() ${\sigma }^2={\Sigma }^2$
. In this case the quenched CLT implies the CLT for
${\sigma }^2={\Sigma }^2$
. In this case the quenched CLT implies the CLT for
![]() $S_n\varphi $
by integrating
$S_n\varphi $
by integrating
![]() $\mu _{\omega }(\{x: S_n^{\omega }\varphi (x)-\mu _{\omega }(S_n^{\omega }\varphi )\leq t\sqrt n\})$
with respect to
$\mu _{\omega }(\{x: S_n^{\omega }\varphi (x)-\mu _{\omega }(S_n^{\omega }\varphi )\leq t\sqrt n\})$
with respect to
![]() ${\mathbb P}$
(and similarly other distributive limit theorems for the skew product follow from the quenched ones). However, it is less likely to be true when
${\mathbb P}$
(and similarly other distributive limit theorems for the skew product follow from the quenched ones). However, it is less likely to be true when
![]() $\mu _{\omega }(\varphi _{\omega })$
depends on
$\mu _{\omega }(\varphi _{\omega })$
depends on
![]() ${\omega }$
. Remark that even when
${\omega }$
. Remark that even when
![]() $\mu _{\omega }(\varphi _{\omega })$
does not depend on
$\mu _{\omega }(\varphi _{\omega })$
does not depend on
![]() ${\omega }$
other finer results like the ASIP do not follow by integration. Indeed the ASIP concerns an almost sure approximation of the partial sums in question by a sum of independent Gaussian random variables, but the quenched ASIP provides a construction of such a Gaussian process which depends on the fiber
${\omega }$
other finer results like the ASIP do not follow by integration. Indeed the ASIP concerns an almost sure approximation of the partial sums in question by a sum of independent Gaussian random variables, but the quenched ASIP provides a construction of such a Gaussian process which depends on the fiber
![]() ${\omega }$
.
${\omega }$
.
1.2.1 Annealed limit theorems: i.i.d. maps
A particular well-studied case is when the maps
![]() $T_{{\sigma }^j{\omega }}$
are independent. That is,
$T_{{\sigma }^j{\omega }}$
are independent. That is,
![]() ${\Omega }={\mathcal Y}^{\mathbb Z}$
is a product space, the coordinates
${\Omega }={\mathcal Y}^{\mathbb Z}$
is a product space, the coordinates
![]() ${\omega }_j$
of
${\omega }_j$
of
![]() ${\omega }=({\omega }_j)$
are independent (with
${\omega }=({\omega }_j)$
are independent (with
![]() ${\sigma }$
being the left shift) and
${\sigma }$
being the left shift) and
![]() $T_{\omega }=T_{{\omega }_0}$
depends only on the zeroth coordinate. In this case the statistical behavior of the skew product
$T_{\omega }=T_{{\omega }_0}$
depends only on the zeroth coordinate. In this case the statistical behavior of the skew product
![]() $\tau $
can be investigated using the so-called annealed transfer operator, given by (see [Reference Baladi8, Reference Baladi and Young9, Reference Ishitani35])
$\tau $
can be investigated using the so-called annealed transfer operator, given by (see [Reference Baladi8, Reference Baladi and Young9, Reference Ishitani35])
where
![]() ${\mathcal L}_{\omega }$
is the transfer operator corresponding to
${\mathcal L}_{\omega }$
is the transfer operator corresponding to
![]() $T_{\omega }$
and the underlying reference measure m. In [Reference Aimino, Nicol and Vaienti2] it was shown that for several classes of random expanding maps, the operator
$T_{\omega }$
and the underlying reference measure m. In [Reference Aimino, Nicol and Vaienti2] it was shown that for several classes of random expanding maps, the operator
![]() ${\mathcal A}$
is quasicompact. Using that, a variety of limit theorems were obtained (such as a CLT, a Berry–Esseen theorem, a local CLT, a local large-deviations principle and an ASIP) for random variables of the form
${\mathcal A}$
is quasicompact. Using that, a variety of limit theorems were obtained (such as a CLT, a Berry–Esseen theorem, a local CLT, a local large-deviations principle and an ASIP) for random variables of the form
 $$ \begin{align*} S_n\varphi({\omega},x)=\sum_{j=0}^{n-1}\varphi(T_{{\omega}_{j-1}}\circ\cdots\circ T_{{\omega}_0}x), \end{align*} $$
$$ \begin{align*} S_n\varphi({\omega},x)=\sum_{j=0}^{n-1}\varphi(T_{{\omega}_{j-1}}\circ\cdots\circ T_{{\omega}_0}x), \end{align*} $$
where
![]() $({\omega },x)$
are distributed according to a
$({\omega },x)$
are distributed according to a
![]() $\tau $
-invariant measure
$\tau $
-invariant measure
![]() $\mu $
of the form
$\mu $
of the form
![]() ${{\mathbb P}\times (h\,dm)}$
for some continuous function h, which satisfies
${{\mathbb P}\times (h\,dm)}$
for some continuous function h, which satisfies
![]() ${\mathcal A} h=h$
. The latter assumption means that the maps
${\mathcal A} h=h$
. The latter assumption means that the maps
![]() $T_{\omega }$
preserve the same measure
$T_{\omega }$
preserve the same measure
![]() $\nu =h\, dm$
. The point is that once quasicompactness is achieved the classical Nagaev–Guivarch method (see [Reference Hennion and Hervé33]) can be applied. This method was applied successfully to obtain limit theorems for deterministic dynamical systems (that is, when
$\nu =h\, dm$
. The point is that once quasicompactness is achieved the classical Nagaev–Guivarch method (see [Reference Hennion and Hervé33]) can be applied. This method was applied successfully to obtain limit theorems for deterministic dynamical systems (that is, when
![]() $T_{\omega }=T$
does not depend on
$T_{\omega }=T$
does not depend on
![]() ${\omega }$
), and in [Reference Aimino, Nicol and Vaienti2] (see also [Reference Ayyer, Liverani and Stenlund7]) this method was applied to obtain annealed limit theorems. We note that since both the function
${\omega }$
), and in [Reference Aimino, Nicol and Vaienti2] (see also [Reference Ayyer, Liverani and Stenlund7]) this method was applied to obtain annealed limit theorems. We note that since both the function
![]() $\varphi $
and the measure
$\varphi $
and the measure
![]() $h \,dm$
do not depend on
$h \,dm$
do not depend on
![]() ${\omega }$
, and all the maps
${\omega }$
, and all the maps
![]() $T_{\omega }$
preserve the measure
$T_{\omega }$
preserve the measure
![]() $h \,dm$
, the fiberwise centering constant
$h \,dm$
, the fiberwise centering constant
![]() $\mu _{\omega }(S_n^{\omega }\varphi )$
and the usual centering constant
$\mu _{\omega }(S_n^{\omega }\varphi )$
and the usual centering constant
![]() $\mu (S_n\varphi )$
are both equal to
$\mu (S_n\varphi )$
are both equal to
![]() $n\int \varphi (x)h(x)\,dm(x)$
. Hence, as discussed in the previous section, in this setup some annealed results such as the CLT already follow from the quenched ones.
$n\int \varphi (x)h(x)\,dm(x)$
. Hence, as discussed in the previous section, in this setup some annealed results such as the CLT already follow from the quenched ones.
Independence here is crucial, since it yields that the iterates on the annealed transfer operator can be written as
where
![]() ${\mathcal L}_{\omega }^n={\mathcal L}_{{\sigma }^{n-1}{\omega }}\circ \cdots \circ {\mathcal L}_{{\sigma }{\omega }}\circ {\mathcal L}_{\omega }$
, which is the transfer operator of
${\mathcal L}_{\omega }^n={\mathcal L}_{{\sigma }^{n-1}{\omega }}\circ \cdots \circ {\mathcal L}_{{\sigma }{\omega }}\circ {\mathcal L}_{\omega }$
, which is the transfer operator of
![]() $T_{\omega }^n$
. Hence, the statistical behavior of the iterates
$T_{\omega }^n$
. Hence, the statistical behavior of the iterates
![]() $\tau ^n$
of the skew product can be described by the iterates of
$\tau ^n$
of the skew product can be described by the iterates of
![]() ${\mathcal A}$
. Note that in this independent and identically distributed (i.i.d.) setup this approach works only when
${\mathcal A}$
. Note that in this independent and identically distributed (i.i.d.) setup this approach works only when
![]() $\varphi ({\omega },x)=\varphi (x)$
does not depend on
$\varphi ({\omega },x)=\varphi (x)$
does not depend on
![]() ${\omega }$
since it requires substituting
${\omega }$
since it requires substituting
![]() $\varphi $
(and appropriate functions of
$\varphi $
(and appropriate functions of
![]() $\varphi $
) into the annealed operator.
$\varphi $
) into the annealed operator.
1.2.2 The motivation behind the present paper: non-i.i.d. maps and random functions
The starting point of this paper is the observation that when the coordinates
![]() $({\omega }_j)$
are not independent (that is, that maps
$({\omega }_j)$
are not independent (that is, that maps
![]() $T_{{\sigma }^j{\omega }}$
are not i.i.d.) there is no apparent relation between the iterates
$T_{{\sigma }^j{\omega }}$
are not i.i.d.) there is no apparent relation between the iterates
![]() $\tau ^n$
of
$\tau ^n$
of
![]() $\tau $
and the iterates of the annealed operator
$\tau $
and the iterates of the annealed operator
![]() ${\mathcal A}$
defined above. Thus, a natural question arising from [Reference Aimino, Nicol and Vaienti2, Reference Ayyer, Liverani and Stenlund7] is which limit theorems hold true for mixing base maps with non-independent coordinates, and functions
${\mathcal A}$
defined above. Thus, a natural question arising from [Reference Aimino, Nicol and Vaienti2, Reference Ayyer, Liverani and Stenlund7] is which limit theorems hold true for mixing base maps with non-independent coordinates, and functions
![]() $\varphi $
which depend on
$\varphi $
which depend on
![]() ${\omega }$
. Moreover, the assumptions in [Reference Aimino, Nicol and Vaienti2] require all the maps
${\omega }$
. Moreover, the assumptions in [Reference Aimino, Nicol and Vaienti2] require all the maps
![]() $T_{\omega }$
to preserve the same absolutely continuous measure
$T_{\omega }$
to preserve the same absolutely continuous measure
![]() $\nu =h\, dm$
, and it is also desirable to prove limit theorems without such assumptions. (We refer to [Reference Nicol, Pereira and Török46] for a CLT and large deviations for random i.i.d. intermittent maps in the case where the
$\nu =h\, dm$
, and it is also desirable to prove limit theorems without such assumptions. (We refer to [Reference Nicol, Pereira and Török46] for a CLT and large deviations for random i.i.d. intermittent maps in the case where the
![]() $T_{\omega }$
do not preserve the same measure.) We note that without the above assumptions even the CLT was not obtained before for the skew products considered in this paper, which will be our first result.
$T_{\omega }$
do not preserve the same measure.) We note that without the above assumptions even the CLT was not obtained before for the skew products considered in this paper, which will be our first result.
The question described above was also one of the main motivations in [Reference Hafouta26], where a CLT, a local CLT and a renewal theorem were obtained for several classes of skew products with mixing base maps such as Markov shifts and non-uniform Young towers, together with uniformly expanding random maps. These results were obtained by a certain type of integration argument; however, the method of [Reference Hafouta26] does not involve the iterates of an annealed transfer operator, and instead we studied directly integrals of the form
![]() $\int {\mathcal L}_{{\omega }}^ng_{\omega }\, d{\mathbb P}({\omega })$
, and their complex perturbations (relying on the fiberwise ‘spectral’ properties and a certain type of periodic point approach which was introduced in [Reference Hafouta and Kifer31]). While [Reference Hafouta26] was the first paper to discuss limit theorem for skew products with non-independent fiber maps and random observables, all the results there were obtained for fiberwise centered observables
$\int {\mathcal L}_{{\omega }}^ng_{\omega }\, d{\mathbb P}({\omega })$
, and their complex perturbations (relying on the fiberwise ‘spectral’ properties and a certain type of periodic point approach which was introduced in [Reference Hafouta and Kifer31]). While [Reference Hafouta26] was the first paper to discuss limit theorem for skew products with non-independent fiber maps and random observables, all the results there were obtained for fiberwise centered observables
![]() $\varphi $
(that is,
$\varphi $
(that is,
![]() $\mu _{\omega }(\varphi _{\omega })=0$
). Moreover, the maps
$\mu _{\omega }(\varphi _{\omega })=0$
). Moreover, the maps
![]() $T_{\omega }$
in [Reference Hafouta26] were uniformly expanding, the base map had a periodic point and the random transfer operator satisfied certain regularity assumptions as functions of
$T_{\omega }$
in [Reference Hafouta26] were uniformly expanding, the base map had a periodic point and the random transfer operator satisfied certain regularity assumptions as functions of
![]() ${\omega }$
around the periodic orbit. From this point of view, a second motivation for the present paper is to prove limit theorems for skew products with non-independent fiber maps
${\omega }$
around the periodic orbit. From this point of view, a second motivation for the present paper is to prove limit theorems for skew products with non-independent fiber maps
![]() $T_{{\sigma }^j{\omega }}$
without the fiberwise centralization assumption and without additional topological assumptions such as the behavior around a periodic orbit. We note that, apart from the CLT, we did not consider in [Reference Hafouta26] any of the limit theorems obtained in the present paper, and so almost all the results in the present paper are new even under the fiberwise centering assumption.
$T_{{\sigma }^j{\omega }}$
without the fiberwise centralization assumption and without additional topological assumptions such as the behavior around a periodic orbit. We note that, apart from the CLT, we did not consider in [Reference Hafouta26] any of the limit theorems obtained in the present paper, and so almost all the results in the present paper are new even under the fiberwise centering assumption.
1.3 Our new results and the method of the proofs
As explained in the previous section, the goal of this paper is to obtain limit theorems with deterministic centering conditions for skew products
![]() $\tau $
built over mixing base maps and non-uniformly expanding maps
$\tau $
built over mixing base maps and non-uniformly expanding maps
![]() $T_{\omega }$
. More precisely, we still consider a product space
$T_{\omega }$
. More precisely, we still consider a product space
![]() ${\Omega }={\mathcal Y}^{\mathbb Z}$
, but with ‘weakly dependent’ coordinates
${\Omega }={\mathcal Y}^{\mathbb Z}$
, but with ‘weakly dependent’ coordinates
![]() ${\omega }_j$
instead of independent ones. We consider a family of non-uniformly expanding maps
${\omega }_j$
instead of independent ones. We consider a family of non-uniformly expanding maps
![]() $T_{\omega }=T_{{\omega }_0}$
and observables of the form
$T_{\omega }=T_{{\omega }_0}$
and observables of the form
![]() $\varphi ({\omega },x)=\varphi _{{\omega }_0}(x)$
and prove limit theorems for sequences of the form
$\varphi ({\omega },x)=\varphi _{{\omega }_0}(x)$
and prove limit theorems for sequences of the form
![]() $Z_n=S_n\varphi -n\int \varphi\, d\mu $
, where
$Z_n=S_n\varphi -n\int \varphi\, d\mu $
, where
 $$ \begin{align*} S_n\varphi({\omega},x)=\sum_{j=0}^{n-1}\varphi_{{\omega}_j}(T_{{\omega}_{j-1}}\circ\cdots\circ T_{{\omega}_0}x)=\sum_{j=0}^{n-1}\varphi_{\sigma^j{\omega}}(T_{{\omega}}^jx) \end{align*} $$
$$ \begin{align*} S_n\varphi({\omega},x)=\sum_{j=0}^{n-1}\varphi_{{\omega}_j}(T_{{\omega}_{j-1}}\circ\cdots\circ T_{{\omega}_0}x)=\sum_{j=0}^{n-1}\varphi_{\sigma^j{\omega}}(T_{{\omega}}^jx) \end{align*} $$
considered as a random variables on the probability space
![]() $({\Omega }\times X,{\mathcal F}\times {\mathcal B},\mu )$
, where
$({\Omega }\times X,{\mathcal F}\times {\mathcal B},\mu )$
, where
![]() $\mu =\int \mu _{\omega }\, d{\mathbb P}$
is the unique
$\mu =\int \mu _{\omega }\, d{\mathbb P}$
is the unique
![]() $\tau $
-invariant measure with
$\tau $
-invariant measure with
![]() $\mu _{\omega }$
being absolutely continuous with respect to m (or when
$\mu _{\omega }$
being absolutely continuous with respect to m (or when
![]() $\mu _{\omega }$
is a random Gibbs measure). In this setup we have
$\mu _{\omega }$
is a random Gibbs measure). In this setup we have
![]() $(T_{{\omega }})_*\mu _{\omega }=\mu _{{\sigma }{\omega }}$
, and in general the maps
$(T_{{\omega }})_*\mu _{\omega }=\mu _{{\sigma }{\omega }}$
, and in general the maps
![]() $T_{\omega }$
do not preserve the same measure. These results are obtained for a certain type of observables
$T_{\omega }$
do not preserve the same measure. These results are obtained for a certain type of observables
![]() $\varphi $
so that
$\varphi $
so that
![]() $\varphi _{{\omega }}(\cdot )$
has bounded variation, uniformly in
$\varphi _{{\omega }}(\cdot )$
has bounded variation, uniformly in
![]() ${\omega }$
. When the maps
${\omega }$
. When the maps
![]() $T_{\omega }$
are expanding on average we will also have a certain scaling assumption (that is,
$T_{\omega }$
are expanding on average we will also have a certain scaling assumption (that is,
![]() $\operatorname {\mathrm {esssup}}_{{\omega }\in {\Omega }}(K({\omega })\|\varphi _{\omega }\|_{BV})<\infty $
for some tempered random variable K), which was shown in [Reference Dragičević, Hafouta and Sedro22] to be necessary for quenched limit theorems, and which is similarly necessary for obtaining limit theorems for the skew product. In what follows we will always assume that
$\operatorname {\mathrm {esssup}}_{{\omega }\in {\Omega }}(K({\omega })\|\varphi _{\omega }\|_{BV})<\infty $
for some tempered random variable K), which was shown in [Reference Dragičević, Hafouta and Sedro22] to be necessary for quenched limit theorems, and which is similarly necessary for obtaining limit theorems for the skew product. In what follows we will always assume that
![]() $\int \varphi\, d\mu =0$
, which is not really a restriction since we can always replace
$\int \varphi\, d\mu =0$
, which is not really a restriction since we can always replace
![]() $\varphi $
with
$\varphi $
with
![]() $\varphi -\int \varphi\, d\mu $
.
$\varphi -\int \varphi\, d\mu $
.
We obtain our results using two different methods, as described below.
1.3.1 Limit theorems for skew products: (functional) CLT, moment estimates, moderate-deviations and exponential concentration inequalities for
 ${\alpha }$
-mixing driving systems via the method of cumulants
${\alpha }$
-mixing driving systems via the method of cumulants
Recall that the
![]() ${\alpha }$
-mixing (dependence) coefficient between two sub-
${\alpha }$
-mixing (dependence) coefficient between two sub-
![]() ${\sigma }$
-algebras
${\sigma }$
-algebras
![]() ${\mathcal G},{\mathcal H}$
of
${\mathcal G},{\mathcal H}$
of
![]() ${\mathcal F}$
is given by
${\mathcal F}$
is given by
Let
![]() ${\mathcal F}_{-\infty ,k}$
be the
${\mathcal F}_{-\infty ,k}$
be the
![]() ${\sigma }$
-algebra generated by the coordinates
${\sigma }$
-algebra generated by the coordinates
![]() ${\omega }_j$
at places
${\omega }_j$
at places
![]() $j\leq k$
and
$j\leq k$
and
![]() ${\mathcal F}_{m,\infty }$
be the
${\mathcal F}_{m,\infty }$
be the
![]() ${\sigma }$
-algebra generated by the coordinates
${\sigma }$
-algebra generated by the coordinates
![]() ${\omega }_j$
at places
${\omega }_j$
at places
![]() $j\geq m$
. Then the
$j\geq m$
. Then the
![]() ${\alpha }$
-dependence coefficients of the sequence of coordinates
${\alpha }$
-dependence coefficients of the sequence of coordinates
![]() $({\omega }_n)$
are defined by
$({\omega }_n)$
are defined by
where the last equality is due to stationarity of the process
![]() $({\omega }_n)$
.
$({\omega }_n)$
.
We assume first that
![]() ${\alpha }_n=O(e^{-cn^\eta })$
for some
${\alpha }_n=O(e^{-cn^\eta })$
for some
![]() $c,\eta>0$
(that is, it is stretched exponential). The first step towards limit theorems is standard for stationary processes: we show that under the weaker condition
$c,\eta>0$
(that is, it is stretched exponential). The first step towards limit theorems is standard for stationary processes: we show that under the weaker condition
![]() $\sum _{n}n{\alpha }_n<\infty $
, the limit
$\sum _{n}n{\alpha }_n<\infty $
, the limit
exists and that it vanishes if and only if
![]() $\varphi $
admits an appropriate coboundary representation. When
$\varphi $
admits an appropriate coboundary representation. When
![]() $s^2>0$
we show that
$s^2>0$
we show that
![]() $n^{-1/2}S_n$
converges in distribution towards a centered normal random variable with variance
$n^{-1/2}S_n$
converges in distribution towards a centered normal random variable with variance
![]() $s^2$
. More precisely, we obtain the convergence rate
$s^2$
. More precisely, we obtain the convergence rate
 $$ \begin{align*} \sup_{t\in{\mathbb R}}\bigg|\mu(S_n\leq ts\sqrt n)-\frac{1}{\sqrt{2\pi}}\int_{-\infty}^t e^{-(1/2)x^2}dx\bigg|\leq Cn^{-1/({2+4\gamma})},\quad \gamma=1/\eta. \end{align*} $$
$$ \begin{align*} \sup_{t\in{\mathbb R}}\bigg|\mu(S_n\leq ts\sqrt n)-\frac{1}{\sqrt{2\pi}}\int_{-\infty}^t e^{-(1/2)x^2}dx\bigg|\leq Cn^{-1/({2+4\gamma})},\quad \gamma=1/\eta. \end{align*} $$
An annealed CLT (that is, for independent maps) was obtained in [Reference Ayyer, Liverani and Stenlund7] for random toral automorphisms and in [Reference Aimino, Nicol and Vaienti2] for more general maps. When the base map is only mixing (and
![]() $\varphi $
depends on
$\varphi $
depends on
![]() ${\omega }$
) it was obtained in [Reference Hafouta26] for fiberwise centered potentials (that is,
${\omega }$
) it was obtained in [Reference Hafouta26] for fiberwise centered potentials (that is,
![]() ${\mu _{\omega }(\varphi _{\omega })=0}$
). One of the results in this paper is the CLT for stretched exponentially
${\mu _{\omega }(\varphi _{\omega })=0}$
). One of the results in this paper is the CLT for stretched exponentially
![]() ${\alpha }$
-mixing base maps but without the fiberwise centering assumption (in fact, we will obtain a functional CLT; see Theorem 2.19 and the last paragraph of §1.3.1).
${\alpha }$
-mixing base maps but without the fiberwise centering assumption (in fact, we will obtain a functional CLT; see Theorem 2.19 and the last paragraph of §1.3.1).
We also obtain a certain type of large-deviations results, often referred to as a moderate-deviations principle (see [Reference Dembo and Zeitouni14]). These results yield, for instance, that for every closed interval
![]() $[a,b]$
we have
$[a,b]$
we have
 $$ \begin{align*} \lim_{n\to\infty}\frac{1}{a_n^2}\ln\mu\bigg\{({\omega},x):\frac{S_n({\omega},x)}{a_nsn^{1/2}}\in[a,b]\bigg\}=-\frac12\inf_{x\in[a,b]}x^2, \end{align*} $$
$$ \begin{align*} \lim_{n\to\infty}\frac{1}{a_n^2}\ln\mu\bigg\{({\omega},x):\frac{S_n({\omega},x)}{a_nsn^{1/2}}\in[a,b]\bigg\}=-\frac12\inf_{x\in[a,b]}x^2, \end{align*} $$
where
![]() $a_n$
is a sequence such that
$a_n$
is a sequence such that
![]() $a_n\to \infty $
and
$a_n\to \infty $
and
![]() $a_n=o(n^{{1}/({2+4{\gamma }})})$
. We also obtain several types of ‘stretched’ exponential concentration inequalities ((2.20), (2.21)) and Gaussian moment estimates of Rosenthal type (2.22). These result are obtained using the method of cumulants. More precisely, we first obtain a certain type of multiple correlation estimates (see Proposition 3.4), and then by applying a general theorem we conclude that the kth cumulant of the sum
$a_n=o(n^{{1}/({2+4{\gamma }})})$
. We also obtain several types of ‘stretched’ exponential concentration inequalities ((2.20), (2.21)) and Gaussian moment estimates of Rosenthal type (2.22). These result are obtained using the method of cumulants. More precisely, we first obtain a certain type of multiple correlation estimates (see Proposition 3.4), and then by applying a general theorem we conclude that the kth cumulant of the sum
![]() $S_n$
is at most of order
$S_n$
is at most of order
![]() $ n(k{!})^{1+{\gamma }}(c_0)^{k-2}$
for
$ n(k{!})^{1+{\gamma }}(c_0)^{k-2}$
for
![]() $k\geq 3$
, where
$k\geq 3$
, where
![]() $c_0$
is some constant (see Theorem 3.1). Then we can apply the method of cumulants [Reference Döring and Eichelsbacher15, Reference Saulis and Statulevicius49]. In the annealed setup, using the quasicompactness of the annealed transfer operator, large-deviations principles and exponential concentration inequalities were obtained in [Reference Aimino, Nicol and Vaienti2], and the above results show that there is a similar behavior when the maps are not independent and the function
$c_0$
is some constant (see Theorem 3.1). Then we can apply the method of cumulants [Reference Döring and Eichelsbacher15, Reference Saulis and Statulevicius49]. In the annealed setup, using the quasicompactness of the annealed transfer operator, large-deviations principles and exponential concentration inequalities were obtained in [Reference Aimino, Nicol and Vaienti2], and the above results show that there is a similar behavior when the maps are not independent and the function
![]() $\varphi $
depends on
$\varphi $
depends on
![]() ${\omega }$
(see also the results in the next section where better exponential concentration inequalities are described).
${\omega }$
(see also the results in the next section where better exponential concentration inequalities are described).
The above multiple correlation estimates together with the method of cumulants and the Rosenthal-type moment estimates also yield a functional CLT. Let us consider the random function
![]() ${\mathcal S}_n(t)=n^{-1/2}S_{[nt]}$
on
${\mathcal S}_n(t)=n^{-1/2}S_{[nt]}$
on
![]() $[0,1]$
. Then we show that it converges in distribution in the Skorokhod space
$[0,1]$
. Then we show that it converges in distribution in the Skorokhod space
![]() $D[0,1]$
to
$D[0,1]$
to
![]() $sW$
, where W is a standard Brownian motion and
$sW$
, where W is a standard Brownian motion and
![]() $s^2=\lim _{n\to \infty }( 1/n)\mathrm {Var}_\mu (S_n)$
.
$s^2=\lim _{n\to \infty }( 1/n)\mathrm {Var}_\mu (S_n)$
.
1.3.2 Limit theorems for skew products with
 $\phi $
- or
$\phi $
- or
 $\psi $
-mixing driving systems via martingale methods: almost sure invariance principle, concentration inequalities and maximal moment estimates
$\psi $
-mixing driving systems via martingale methods: almost sure invariance principle, concentration inequalities and maximal moment estimates
One of the strongest methods to prove CLTs and related results in probability theory and dynamical systems is the so-called martingale-coboundary representation (Gordin’s method). For a sufficiently chaotic dynamical system
![]() $(Y,{\mathcal G},\mu ,T)$
and an observable
$(Y,{\mathcal G},\mu ,T)$
and an observable
![]() $\varphi :Y\to {\mathbb R}$
it means that
$\varphi :Y\to {\mathbb R}$
it means that
![]() $\varphi $
can be represented as
$\varphi $
can be represented as
![]() $\varphi =u+\chi -\chi \circ T$
for some sufficiently regular function
$\varphi =u+\chi -\chi \circ T$
for some sufficiently regular function
![]() $\chi $
, and
$\chi $
, and
![]() $(u\circ T^n)$
forms a reverse martingale difference. Such results are well known for deterministic expanding (or hyperbolic) dynamical systems, and we refer to [Reference Dragičević, Froyland, González-Tokman and Vaienti16, Reference Dragičević, Hafouta and Sedro22, Reference Korepanov, Kosloff and Melbourne42] for quenched and sequential versions of such martingale methods.
$(u\circ T^n)$
forms a reverse martingale difference. Such results are well known for deterministic expanding (or hyperbolic) dynamical systems, and we refer to [Reference Dragičević, Froyland, González-Tokman and Vaienti16, Reference Dragičević, Hafouta and Sedro22, Reference Korepanov, Kosloff and Melbourne42] for quenched and sequential versions of such martingale methods.
Recall that the
![]() $\phi $
-mixing and
$\phi $
-mixing and
![]() $\psi $
(dependence) coefficient between two sub-
$\psi $
(dependence) coefficient between two sub-
![]() ${\sigma }$
-algebras
${\sigma }$
-algebras
![]() ${\mathcal G},{\mathcal H}$
of
${\mathcal G},{\mathcal H}$
of
![]() ${\mathcal F}$
is given by
${\mathcal F}$
is given by
and
 $$ \begin{align*} \psi({\mathcal G},{\mathcal H})=\sup\bigg\{\bigg|\frac{{\mathbb P}(A\cap B)}{{\mathbb P}(A){\mathbb P}(B)}-1\bigg|: A\in{\mathcal G}, B\in{\mathcal H}, {\mathbb P}(A){\mathbb P}(B)>0\bigg\}. \end{align*} $$
$$ \begin{align*} \psi({\mathcal G},{\mathcal H})=\sup\bigg\{\bigg|\frac{{\mathbb P}(A\cap B)}{{\mathbb P}(A){\mathbb P}(B)}-1\bigg|: A\in{\mathcal G}, B\in{\mathcal H}, {\mathbb P}(A){\mathbb P}(B)>0\bigg\}. \end{align*} $$
The reverse
![]() $\phi $
-mixing coefficients of the sequence of coordinates
$\phi $
-mixing coefficients of the sequence of coordinates
![]() $({\omega }_n)$
are defined by
$({\omega }_n)$
are defined by
while the
![]() $\psi $
-mixing coefficients of
$\psi $
-mixing coefficients of
![]() $(\xi _n)$
are defined by
$(\xi _n)$
are defined by
where
![]() ${\mathcal F}_{n,m}$
is as defined before (1.2). It is clear from the definitions of the mixing coefficients that
${\mathcal F}_{n,m}$
is as defined before (1.2). It is clear from the definitions of the mixing coefficients that
When the sequence
![]() $({\omega }_n)$
is (sufficiently fast)
$({\omega }_n)$
is (sufficiently fast)
![]() $\phi $
- or
$\phi $
- or
![]() $\psi $
-mixing we obtain a certain type of
$\psi $
-mixing we obtain a certain type of
![]() $L^\infty $
martingale-coboundary representation (that is,
$L^\infty $
martingale-coboundary representation (that is,
![]() $\chi \in L^\infty $
) for the underlying class of observables
$\chi \in L^\infty $
) for the underlying class of observables
![]() $\varphi $
with respect to the skew product
$\varphi $
with respect to the skew product
![]() $\tau $
. This was already established in [Reference Aimino, Nicol and Vaienti2] in the annealed setup (that is, when
$\tau $
. This was already established in [Reference Aimino, Nicol and Vaienti2] in the annealed setup (that is, when
![]() $({\omega }_n)$
is an i.i.d. sequence), and here, using different arguments, we obtain such a representation for skew products with mixing base maps.
$({\omega }_n)$
is an i.i.d. sequence), and here, using different arguments, we obtain such a representation for skew products with mixing base maps.
Once an
![]() $L^\infty $
martingale-coboundary decomposition is achieved, as usual, we can apply the Azuma–Hoeffding inequality together with Chernoff’s bounding method and obtain exponential concentration inequalities of the form
$L^\infty $
martingale-coboundary decomposition is achieved, as usual, we can apply the Azuma–Hoeffding inequality together with Chernoff’s bounding method and obtain exponential concentration inequalities of the form
where
![]() $c_1,c_2,c_3$
are positive constants. These concentration inequities are better than the ones we obtain using the method of cumulants, although they involve the stronger notions of
$c_1,c_2,c_3$
are positive constants. These concentration inequities are better than the ones we obtain using the method of cumulants, although they involve the stronger notions of
![]() $\phi $
- or
$\phi $
- or
![]() $\psi $
-mixing instead of
$\psi $
-mixing instead of
![]() ${\alpha }$
-mixing. (However, they only require summable
${\alpha }$
-mixing. (However, they only require summable
![]() $\phi $
- or
$\phi $
- or
![]() $\psi $
-mixing coefficients and not stretched exponential ones.) Another immediate consequence is moment estimates of the form
$\psi $
-mixing coefficients and not stretched exponential ones.) Another immediate consequence is moment estimates of the form
which hold for every
![]() $1\leq p<\infty $
. Such results are known in the annealed case [Reference Aimino, Nicol and Vaienti2], and we extend them to the skew products considered in this paper.
$1\leq p<\infty $
. Such results are known in the annealed case [Reference Aimino, Nicol and Vaienti2], and we extend them to the skew products considered in this paper.
The idea behind the martingale-coboundary representation is as follows. Consider the sub-
![]() ${\sigma }$
-algebra
${\sigma }$
-algebra
![]() ${\mathcal F}_0$
of
${\mathcal F}_0$
of
![]() ${\Omega }\times X$
generated by the projection
${\Omega }\times X$
generated by the projection
![]() $\pi _0({\omega },x)=(({\omega }_j)_{j\geq 0},x)$
, where
$\pi _0({\omega },x)=(({\omega }_j)_{j\geq 0},x)$
, where
![]() ${\omega }=({\omega }_j)_{j\in {\mathbb Z}}$
. Then
${\omega }=({\omega }_j)_{j\in {\mathbb Z}}$
. Then
![]() $\tau $
preserves
$\tau $
preserves
![]() ${\mathcal F}_0$
since
${\mathcal F}_0$
since
![]() $T_{\omega }=T_{{\omega }_0}$
depends only on
$T_{\omega }=T_{{\omega }_0}$
depends only on
![]() ${\omega }_0$
, and
${\omega }_0$
, and
![]() ${\mathcal F}_0$
can be viewed as a subsystem (or a factor) given by
${\mathcal F}_0$
can be viewed as a subsystem (or a factor) given by
![]() $({\Omega }\times X,{\mathcal F}_0,\mu ,\tau )$
. Our main argument is as follows. Let
$({\Omega }\times X,{\mathcal F}_0,\mu ,\tau )$
. Our main argument is as follows. Let
![]() ${\mathcal K}$
be the transfer operator corresponding to the invariant
${\mathcal K}$
be the transfer operator corresponding to the invariant
![]() ${\sigma }$
-algebra
${\sigma }$
-algebra
![]() ${\mathcal F}_0$
, namely the one defined by the duality relation
${\mathcal F}_0$
, namely the one defined by the duality relation
where
![]() $g\in L^1({\Omega }\times X,{\mathcal F}_0,\mu )$
and
$g\in L^1({\Omega }\times X,{\mathcal F}_0,\mu )$
and
![]() $f\in L^\infty ({\Omega }\times X,{\mathcal F}_0,\mu )$
. Then we show that, under quite mild
$f\in L^\infty ({\Omega }\times X,{\mathcal F}_0,\mu )$
. Then we show that, under quite mild
![]() $\phi $
- or
$\phi $
- or
![]() $\psi $
-mixing rates for the sequence of coordinates
$\psi $
-mixing rates for the sequence of coordinates
![]() $({\omega }_n)$
, the iterates
$({\omega }_n)$
, the iterates
![]() ${\mathcal K}^{\,n} \varphi $
of the transfer operator
${\mathcal K}^{\,n} \varphi $
of the transfer operator
![]() ${\mathcal K}$
corresponding to this system converge fast enough in
${\mathcal K}$
corresponding to this system converge fast enough in
![]() $L^\infty (\mu )$
towards
$L^\infty (\mu )$
towards
![]() $\mu (\varphi )\textbf {1}$
, where
$\mu (\varphi )\textbf {1}$
, where
![]() $\textbf {1}$
is the function taking the constant value
$\textbf {1}$
is the function taking the constant value
![]() $1$
, and
$1$
, and
![]() $\varphi $
is our given observable. This convergence can be established for every function
$\varphi $
is our given observable. This convergence can be established for every function
![]() $\varphi $
so that
$\varphi $
so that
![]() $\|\varphi \|_{K,2}=\text {esssup}_{{\omega }\in {\Omega }}(K({\omega })^2\|\varphi ({\omega },\cdot )\|_{BV})<\infty $
for an appropriate tempered random variable
$\|\varphi \|_{K,2}=\text {esssup}_{{\omega }\in {\Omega }}(K({\omega })^2\|\varphi ({\omega },\cdot )\|_{BV})<\infty $
for an appropriate tempered random variable
![]() $K({\omega })$
, or for any observable with
$K({\omega })$
, or for any observable with
![]() $\operatorname {\mathrm {esssup}}_{{\omega }\in {\Omega }}\|\varphi ({\omega },\cdot )\|_{BV}<\infty $
when the maps
$\operatorname {\mathrm {esssup}}_{{\omega }\in {\Omega }}\|\varphi ({\omega },\cdot )\|_{BV}<\infty $
when the maps
![]() $T_{\omega }$
are uniformly expanding. We stress that in any case this is not a spectral result (even under exponential mixing), since the convergence of
$T_{\omega }$
are uniformly expanding. We stress that in any case this is not a spectral result (even under exponential mixing), since the convergence of
![]() ${\mathcal K}^{\,n}$
is not in an operator norm, and, in general, it does not have an exponential rate. Indeed, we only prove that
${\mathcal K}^{\,n}$
is not in an operator norm, and, in general, it does not have an exponential rate. Indeed, we only prove that
where
![]() $\gamma _n={\delta }^n+\phi _R([n/2])$
or
$\gamma _n={\delta }^n+\phi _R([n/2])$
or
![]() $\gamma _n={\delta }^n+\psi ([n/2])$
, and
$\gamma _n={\delta }^n+\psi ([n/2])$
, and
![]() ${\delta }\in (0,1)$
and
${\delta }\in (0,1)$
and
![]() $\phi _R(\cdot )$
and
$\phi _R(\cdot )$
and
![]() $\psi (\cdot )$
are the reverse
$\psi (\cdot )$
are the reverse
![]() $\phi $
-mixing coefficients and
$\phi $
-mixing coefficients and
![]() $\psi $
-mixing coefficients defined in (1.3) and (1.4), respectively.
$\psi $
-mixing coefficients defined in (1.3) and (1.4), respectively.
Another consequence of the martingale-coboundary representation is the ASIP, which in our context concerns almost sure approximation of the Birkhoff sum by Gaussians. The ASIP for random (and sequential) dynamical systems has been studied by several authors in recent years (see, for instance, [Reference Dragičević, Froyland, González-Tokman and Vaienti16, Reference Dragičević, Hafouta, Pollicott and Vaienti20–Reference Dragičević, Hafouta and Sedro22, Reference Haydn, Nicol, Török and Vaienti32, Reference Su50, Reference Su51]), and in this paper we will focus on the ASIP for Birkhoff sums generated by the skew product.
In [Reference Cuny and Merlevede13] the authors proved that, under certain assumptions, a reverse martingale
![]() $M_n$
can be approximated almost surely by a sum of independent Gaussians. One consequence of the methods in [Reference Cuny and Merlevede13] is for sums of the form
$M_n$
can be approximated almost surely by a sum of independent Gaussians. One consequence of the methods in [Reference Cuny and Merlevede13] is for sums of the form
![]() $W_n=\sum _{j=0}^{n-1}\varphi \circ \tau ^j$
. For such sums, the conditions of [Reference Cuny and Merlevede13, Theorem 3.2] show that there is a coupling with a sequence of i.i.d. centered normal random variables
$W_n=\sum _{j=0}^{n-1}\varphi \circ \tau ^j$
. For such sums, the conditions of [Reference Cuny and Merlevede13, Theorem 3.2] show that there is a coupling with a sequence of i.i.d. centered normal random variables
![]() $Z_j$
with variance
$Z_j$
with variance
![]() $s^2=\lim _{n\to \infty }(1/n)\mathrm {Var}(W_n)$
so that
$s^2=\lim _{n\to \infty }(1/n)\mathrm {Var}(W_n)$
so that
 $$ \begin{align*} \sup_{1\leq k\leq n}\bigg|W_k-\sum_{j=1}^k Z_j\bigg|=O(n^{1/4}(\log n)^{1/2}(\log\log n)^{1/4})\quad\text{almost surely}. \end{align*} $$
$$ \begin{align*} \sup_{1\leq k\leq n}\bigg|W_k-\sum_{j=1}^k Z_j\bigg|=O(n^{1/4}(\log n)^{1/2}(\log\log n)^{1/4})\quad\text{almost surely}. \end{align*} $$
In our notation, the first and second conditions of [Reference Cuny and Merlevede13, Theorem 3.2] about
![]() ${\mathcal K}$
can be verified using (1.5). In order to show that the third (and last condition) about
${\mathcal K}$
can be verified using (1.5). In order to show that the third (and last condition) about
![]() ${\mathcal K}$
in [Reference Cuny and Merlevede13, Theorem 3.2] is in force we will also need to provide more general estimates on expression of the form
${\mathcal K}$
in [Reference Cuny and Merlevede13, Theorem 3.2] is in force we will also need to provide more general estimates on expression of the form
for
![]() $1\leq i,j\leq n$
, where
$1\leq i,j\leq n$
, where
![]() $\bar \varphi =\varphi -\mu (\varphi )$
.
$\bar \varphi =\varphi -\mu (\varphi )$
.
We note that in [Reference Aimino, Nicol and Vaienti2] the annealed ASIP was obtained using Gouëzel’s approach [Reference Gouëzel24] and not the martingale-coboundary approach. Gouëzel’s approach was also used in [Reference Atnip5] to obtain an ASIP for non-independent maps with mixing base maps, but as indicated in [Reference Atnip5] the results are mostly applicable for Gordin–Denker maps.
Finally, we also prove a vector-valued ASIP for skew products with uniformly expanding random maps and exponentially fast
![]() ${\alpha }$
-mixing base maps via the method of Gouëzel [Reference Gouëzel24]. As we have mentioned above, this method was applied in [Reference Aimino, Nicol and Vaienti2] in the annealed setting, while in [Reference Atnip5] it was applied for Gordin–Denker systems. In a final section we also discuss a few extensions such as different types of mixing base maps such as Young towers or Gibbs–Markov maps, application of the method of cumulants for non-conventional sums of the form
${\alpha }$
-mixing base maps via the method of Gouëzel [Reference Gouëzel24]. As we have mentioned above, this method was applied in [Reference Aimino, Nicol and Vaienti2] in the annealed setting, while in [Reference Atnip5] it was applied for Gordin–Denker systems. In a final section we also discuss a few extensions such as different types of mixing base maps such as Young towers or Gibbs–Markov maps, application of the method of cumulants for non-conventional sums of the form
![]() $S_n=\sum _{m=1}^n\prod _{j=1}^\ell \varphi _j\circ \tau ^{q_j(m)}$
, for polynomial
$S_n=\sum _{m=1}^n\prod _{j=1}^\ell \varphi _j\circ \tau ^{q_j(m)}$
, for polynomial
![]() $q_j(m)$
, as well as extensions of the results for different classes of random expanding maps (the ones in [Reference Mayer, Skorulski and Urbański44]).
$q_j(m)$
, as well as extensions of the results for different classes of random expanding maps (the ones in [Reference Mayer, Skorulski and Urbański44]).
2 Preliminaries and main results
2.1 The random maps
We begin by recalling the setup from [Reference Buzzi12]. Let
![]() $(X, \mathcal G)$
be a measurable space endowed with a probability measure m and a notion of a variation
$(X, \mathcal G)$
be a measurable space endowed with a probability measure m and a notion of a variation
![]() $\mathrm {v} \colon L^1(X, m) \to [0, \infty ]$
which satisfies the following conditions:
$\mathrm {v} \colon L^1(X, m) \to [0, \infty ]$
which satisfies the following conditions:
-
(V1)
 $\mathrm {v} (th)= |t| \mathrm {v} (h)$
;
$\mathrm {v} (th)= |t| \mathrm {v} (h)$
; -
(V2)
 $\mathrm {v} (g+h)\leq \mathrm {v} (g)+\mathrm {v} (h)$
;
$\mathrm {v} (g+h)\leq \mathrm {v} (g)+\mathrm {v} (h)$
; -
(V3)
 $\|h\|_{L^\infty } \le C_{\mathrm {v}}(\|h\|_1+\mathrm {v} (h))$
for some constant
$\|h\|_{L^\infty } \le C_{\mathrm {v}}(\|h\|_1+\mathrm {v} (h))$
for some constant
 $1\leq C_{\mathrm {v}}<\infty $
;
$1\leq C_{\mathrm {v}}<\infty $
; -
(V4) for any
 $C>0$
, the set
$C>0$
, the set
 $\{h\colon X \to \mathbb R: \|h\|_1+\mathrm {v} (h) \leq C\}$
is
$\{h\colon X \to \mathbb R: \|h\|_1+\mathrm {v} (h) \leq C\}$
is
 $L^1(m)$
-compact;
$L^1(m)$
-compact; -
(V5)
 $\mathrm {v}({\boldsymbol 1})=0$
, where
$\mathrm {v}({\boldsymbol 1})=0$
, where
 ${\boldsymbol 1}$
denotes the function equal to
${\boldsymbol 1}$
denotes the function equal to
 $1$
on X;
$1$
on X; -
(V6)
 $\{h \colon X \to \mathbb R_+: \lVert h\rVert _1=1 \ \text {and} \ \mathrm {v} (h)<\infty \}$
is
$\{h \colon X \to \mathbb R_+: \lVert h\rVert _1=1 \ \text {and} \ \mathrm {v} (h)<\infty \}$
is
 $L^1(m)$
-dense in
$L^1(m)$
-dense in
 $\{h\colon X \to \mathbb R_+: \|h\|_1=1\}$
;
$\{h\colon X \to \mathbb R_+: \|h\|_1=1\}$
; -
(V7) for any
 $f\in L^1(X, m)$
such that
$f\in L^1(X, m)$
such that
 $\text {essinf} f>0$
, we have
$\text {essinf} f>0$
, we have  $$ \begin{align*}\mathrm{v}(1/f) \leq \frac{\mathrm{v} (f)}{(\text{essinf} f)^2};\end{align*} $$
$$ \begin{align*}\mathrm{v}(1/f) \leq \frac{\mathrm{v} (f)}{(\text{essinf} f)^2};\end{align*} $$
-
(V8)
 $\mathrm {v} (fg)\leq \|f\|_{L^\infty }\cdot \mathrm {v}(g)+\|g\|_{L^\infty }\cdot \mathrm {v}(f)$
;
$\mathrm {v} (fg)\leq \|f\|_{L^\infty }\cdot \mathrm {v}(g)+\|g\|_{L^\infty }\cdot \mathrm {v}(f)$
; -
(V9) for
 $M\kern1pt{>}\kern1pt0$
,
$M\kern1pt{>}\kern1pt0$
,
 $f\kern1pt{\colon}\kern-1pt X \kern1pt{\to}\kern1pt [-M, M]$
measurable and every
$f\kern1pt{\colon}\kern-1pt X \kern1pt{\to}\kern1pt [-M, M]$
measurable and every
 $C^1$
function
$C^1$
function
 $h\kern0.1pt{\colon}\kern0.1pt [-M, M] \kern0.5pt{\to}\kern0.5pt {\mathbb C}$
, we have
$h\kern0.1pt{\colon}\kern0.1pt [-M, M] \kern0.5pt{\to}\kern0.5pt {\mathbb C}$
, we have
 $\mathrm {v}(h\circ f)\leq \|h'\|_{L^\infty } \cdot \mathrm {v}(f)$
.
$\mathrm {v}(h\circ f)\leq \|h'\|_{L^\infty } \cdot \mathrm {v}(f)$
.
We define
Then
![]() $BV$
is a Banach space with respect to the norm
$BV$
is a Banach space with respect to the norm
Remark 2.1. Observe that (V3) and (V8) imply that
Remark 2.2. We observe that in [Reference Buzzi12], assumption (V5) is replaced by the weaker
![]() . However, for the examples we have in mind, our stronger version is satisfied. In particular, (V5) implies that
. However, for the examples we have in mind, our stronger version is satisfied. In particular, (V5) implies that
![]() $\| {\boldsymbol 1}\|_{BV}=1$
.
$\| {\boldsymbol 1}\|_{BV}=1$
.
The rest of our setup is almost identical to [Reference Dragičević, Hafouta and Sedro22], with a single additional requirement that will be indicated in what follows. Let
![]() $(\Omega , \mathcal {F}, \mathbb P, \sigma )$
, be a probability space and
$(\Omega , \mathcal {F}, \mathbb P, \sigma )$
, be a probability space and
![]() ${\sigma \colon \Omega \to \Omega }$
an invertible ergodic measure-preserving transformation. Let
${\sigma \colon \Omega \to \Omega }$
an invertible ergodic measure-preserving transformation. Let
![]() $T_{\omega } \colon X \to X$
,
$T_{\omega } \colon X \to X$
,
![]() $\omega \in \Omega $
be a collection of non-singular transformations (that is,
$\omega \in \Omega $
be a collection of non-singular transformations (that is,
![]() $m\circ T_\omega ^{-1}\ll m$
for each
$m\circ T_\omega ^{-1}\ll m$
for each
![]() $\omega $
) acting on X. Each transformation
$\omega $
) acting on X. Each transformation
![]() $T_{\omega }$
induces the corresponding transfer operator
$T_{\omega }$
induces the corresponding transfer operator
![]() $\mathcal L_{\omega }$
acting on
$\mathcal L_{\omega }$
acting on
![]() $L^1(X, m)$
and defined by the duality relation
$L^1(X, m)$
and defined by the duality relation
Thus, we obtain a cocycle of transfer operators
![]() $(\Omega , \mathcal F, \mathbb P, \sigma , L^1(X, m), \mathcal L)$
that we denote by
$(\Omega , \mathcal F, \mathbb P, \sigma , L^1(X, m), \mathcal L)$
that we denote by
![]() $\mathcal L=(\mathcal L_\omega )_{\omega \in \Omega }$
. For
$\mathcal L=(\mathcal L_\omega )_{\omega \in \Omega }$
. For
![]() $\omega \in \Omega $
and
$\omega \in \Omega $
and
![]() $n\in \mathbb N$
, set
$n\in \mathbb N$
, set
We recall the notion of a tempered random variable.
Definition 2.3. We say that a measurable map
![]() $K\colon \Omega \to (0, +\infty )$
is tempered if
$K\colon \Omega \to (0, +\infty )$
is tempered if
In this paper we will consider the following assumptions on the random transfer operators.
Definition 2.4. A cocycle
![]() $\mathcal L=(\mathcal L_\omega )_{\omega \in \Omega }$
of transfer operators is said to be good if the following conditions hold.
$\mathcal L=(\mathcal L_\omega )_{\omega \in \Omega }$
of transfer operators is said to be good if the following conditions hold.
-
•
 $\Omega $
is a Borel subset of a separable, complete metric space and
$\Omega $
is a Borel subset of a separable, complete metric space and
 $\sigma $
is a homeomorphism. Moreover,
$\sigma $
is a homeomorphism. Moreover,
 $\mathcal L$
is
$\mathcal L$
is
 $\mathbb P$
-continuous, that is,
$\mathbb P$
-continuous, that is,
 $\Omega $
can be written as a countable union of measurable sets such that
$\Omega $
can be written as a countable union of measurable sets such that
 $\omega \mapsto \mathcal L_\omega $
is continuous on each of those sets.
$\omega \mapsto \mathcal L_\omega $
is continuous on each of those sets. -
• There is a tempered random variable
 $N({\omega })$
such that (2.3)
$N({\omega })$
such that (2.3) $$ \begin{align} v(g\circ T_\omega) \le N(\omega) v(g) \quad \text{for }{\mathbb P}\text{-a.e. }\omega \in \Omega\text{ and }g\in BV. \end{align} $$
$$ \begin{align} v(g\circ T_\omega) \le N(\omega) v(g) \quad \text{for }{\mathbb P}\text{-a.e. }\omega \in \Omega\text{ and }g\in BV. \end{align} $$
-
• There exists a random variable
 $C\colon \Omega \to (0, +\infty )$
such that
$C\colon \Omega \to (0, +\infty )$
such that
 $\log C\in L^1(\Omega , \mathbb P)$
and
$\log C\in L^1(\Omega , \mathbb P)$
and  $$ \begin{align*} \|\mathcal L_\omega h\|_{BV}\le C(\omega) \|h\|_{BV} \quad \text{for }{\mathbb P}\text{-a.e. }\omega \in \Omega\text{ and }h\in BV. \end{align*} $$
$$ \begin{align*} \|\mathcal L_\omega h\|_{BV}\le C(\omega) \|h\|_{BV} \quad \text{for }{\mathbb P}\text{-a.e. }\omega \in \Omega\text{ and }h\in BV. \end{align*} $$
-
• There exist
 $N\in {\mathbb N}$
and random variables
$N\in {\mathbb N}$
and random variables
 $\alpha , K \colon \Omega \to (0, +\infty )$
such that and, for
$\alpha , K \colon \Omega \to (0, +\infty )$
such that and, for $$ \begin{align*} \int_\Omega \log \alpha \, d\mathbb P <0, \quad \log K \in L^1(\Omega, \mathbb P) \end{align*} $$
$$ \begin{align*} \int_\Omega \log \alpha \, d\mathbb P <0, \quad \log K \in L^1(\Omega, \mathbb P) \end{align*} $$
 $\mathbb P$
-a.e.
$\mathbb P$
-a.e.
 $\omega \in \Omega $
and
$\omega \in \Omega $
and
 $h\in BV$
,
$h\in BV$
,  $$ \begin{align*} \mathrm{v}(\mathcal L_\omega^N h) \leq \alpha (\omega) \mathrm{v}(h)+ K(\omega) \|h\|_1. \end{align*} $$
$$ \begin{align*} \mathrm{v}(\mathcal L_\omega^N h) \leq \alpha (\omega) \mathrm{v}(h)+ K(\omega) \|h\|_1. \end{align*} $$
-
• For each
 $a>0$
and
$a>0$
and
 $\mathbb P$
-a.e.
$\mathbb P$
-a.e.
 $\omega \in \Omega $
, there exist random numbers
$\omega \in \Omega $
, there exist random numbers
 $n_c(\omega )<+\infty $
and
$n_c(\omega )<+\infty $
and
 $\alpha _0(\omega ), \alpha _1(\omega ), \ldots $
such that for every
$\alpha _0(\omega ), \alpha _1(\omega ), \ldots $
such that for every
 $h\in \mathcal C_a$
, (2.4)where
$h\in \mathcal C_a$
, (2.4)where $$ \begin{align} \text{essinf}_x (\mathcal L_\omega^n h)(x) \ge \alpha_n\|h \|_1 \quad \text{for }n\ge n_c, \end{align} $$
(2.5)
$$ \begin{align} \text{essinf}_x (\mathcal L_\omega^n h)(x) \ge \alpha_n\|h \|_1 \quad \text{for }n\ge n_c, \end{align} $$
(2.5) $$ \begin{align} \mathcal C_a:=\{ h\in L^\infty (X,m): h\geq 0 \text{ and }\mathrm{v}(h) \leq a\|h\|_1\}. \end{align} $$
$$ \begin{align} \mathcal C_a:=\{ h\in L^\infty (X,m): h\geq 0 \text{ and }\mathrm{v}(h) \leq a\|h\|_1\}. \end{align} $$
-
•
 .
.
Finally, we say that the cocycle
![]() $\mathcal L$
is uniformly random if the random variables
$\mathcal L$
is uniformly random if the random variables
![]() $C,{\alpha }^N, K^N$
and
$C,{\alpha }^N, K^N$
and
![]() $n_c$
are constants and
$n_c$
are constants and
![]() ${\alpha }_n({\omega })$
does not depend on n and
${\alpha }_n({\omega })$
does not depend on n and
![]() ${\omega }$
.
${\omega }$
.
Remark 2.5
-
• Definition 2.4 almost coincides with [Reference Dragičević, Hafouta and Sedro22, Definition 3], the only difference being the addition of (2.3) (which was considered in [Reference Dragičević, Hafouta and Sedro22, §3].)
-
• The log-integrability assumption specified at the end of Definition 2.4 may easily be checked on explicit examples (see, for example, the discussion in [Reference Atnip, Froyland, González-Tokman and Vaienti6, Remark 2.12]).
-
• Furthermore, this assumption implies a certain version of the ‘random covering’ similar to (2.4); see [Reference Dragičević, Hafouta and Sedro22, Remark 4].
Let us now give examples of systems satisfying our requirements. Our first example is essentially taken from [Reference Buzzi12].
Example 2.6. (Lasota–Yorke cocycles)
Consider
![]() $X=[0,1]$
, endowed with Lebesgue measure m and the classical notion of variation
$X=[0,1]$
, endowed with Lebesgue measure m and the classical notion of variation
![]() $\mathrm {v}$
. We say that
$\mathrm {v}$
. We say that
![]() $T:X\to X$
is a piecewise monotonic non-singular (p.m.n.s.) map if the following conditions hold.
$T:X\to X$
is a piecewise monotonic non-singular (p.m.n.s.) map if the following conditions hold.
-
• T is piecewise monotonic, that is, there exists a subdivision
 $0=a_0<a_1<\cdots <a_N=1$
such that for each
$0=a_0<a_1<\cdots <a_N=1$
such that for each
 $i\in \{0,\ldots ,N-1\}$
, the restriction
$i\in \{0,\ldots ,N-1\}$
, the restriction
 $T_i=T_{|(a_i,a_{i+1})}$
is monotonic (in particular, it is a homeomorphism on its image).
$T_i=T_{|(a_i,a_{i+1})}$
is monotonic (in particular, it is a homeomorphism on its image). -
• T is non-singular, that is, there exists
 $|T'|:[0,1]\to \mathbb R_+$
such that, for any measurable
$|T'|:[0,1]\to \mathbb R_+$
such that, for any measurable
 $E\subset (a_i,a_{i+1})$
,
$E\subset (a_i,a_{i+1})$
,
 $m(T(E))=\int _E|T'|\,dm$
.
$m(T(E))=\int _E|T'|\,dm$
.
The intervals
![]() $(a_i,a_{i+1})_{i\in \{0,\ldots ,N-1\}}$
are called the intervals of T. We also set
$(a_i,a_{i+1})_{i\in \{0,\ldots ,N-1\}}$
are called the intervals of T. We also set
![]() $N(T):=N$
and
$N(T):=N$
and
![]() $\unicode{x3bb} (T):=\text {essinf }_{[0,1]}|T'|$
.
$\unicode{x3bb} (T):=\text {essinf }_{[0,1]}|T'|$
.
We consider a family
![]() $(T_\omega )_{\omega \in \Omega }$
of random p.m.n.s. as above, and such that
$(T_\omega )_{\omega \in \Omega }$
of random p.m.n.s. as above, and such that
![]() $T:\Omega \times [0,1]\to [0,1], (\omega ,x)\mapsto T_\omega (x)$
is measurable. Denoting
$T:\Omega \times [0,1]\to [0,1], (\omega ,x)\mapsto T_\omega (x)$
is measurable. Denoting
![]() $N_\omega =N(T_\omega )$
and
$N_\omega =N(T_\omega )$
and
![]() $\unicode{x3bb} _\omega =\unicode{x3bb} (T_\omega )$
, we make the following assumptions.
$\unicode{x3bb} _\omega =\unicode{x3bb} (T_\omega )$
, we make the following assumptions.
-
• The map
 $\omega \mapsto (\mathrm {v}({1}/{|T^{\prime }_\omega |}),N_\omega ,\unicode{x3bb} _\omega ,a_1,\ldots ,a_{N_\omega -1})$
is measurable.
$\omega \mapsto (\mathrm {v}({1}/{|T^{\prime }_\omega |}),N_\omega ,\unicode{x3bb} _\omega ,a_1,\ldots ,a_{N_\omega -1})$
is measurable. -
• We have the following expanding-on-average property:

-
• The maps
 $\log (N_{\omega })$
and
$\log (N_{\omega })$
and
 $\log ^+({N_\omega }/{\unicode{x3bb} _\omega })$
are integrable.
$\log ^+({N_\omega }/{\unicode{x3bb} _\omega })$
are integrable. -
• The map
 $\log ^+(\mathrm {v}({1}/{|T_\omega '|}))$
is integrable.
$\log ^+(\mathrm {v}({1}/{|T_\omega '|}))$
is integrable. -
•
 $T_\omega $
is covering, that is, for any interval
$T_\omega $
is covering, that is, for any interval
 $I\subset [0,1]$
, there exists a random number
$I\subset [0,1]$
, there exists a random number
 $n_c(\omega )>0$
such that, for any
$n_c(\omega )>0$
such that, for any
 $n\ge n_c$
, one has (2.6)
$n\ge n_c$
, one has (2.6)
-
•
 .
.
We will call a cocycle satisfying the previous assumptions an expanding-on-average Lasota–Yorke cocycle. For a countably valued measurable family
![]() $(T_\omega )_{\omega \in \Omega }$
of expanding-on-average Lasota–Yorke cocycles, the associated cocycle of transfer operators
$(T_\omega )_{\omega \in \Omega }$
of expanding-on-average Lasota–Yorke cocycles, the associated cocycle of transfer operators
![]() $(\mathcal L_\omega )_{\omega \in \Omega }$
is good (see [Reference Dragičević and Sedro23]).
$(\mathcal L_\omega )_{\omega \in \Omega }$
is good (see [Reference Dragičević and Sedro23]).
The following example can be fruitfully compared to a similar one by Kifer [Reference Kifer38].
Example 2.7. We consider
![]() $X=\mathbb S^1$
, endowed with the Lebesgue measure m and the notion of variation given by
$X=\mathbb S^1$
, endowed with the Lebesgue measure m and the notion of variation given by
![]() $\mathrm {v}(\phi ):=\int _X |\phi '|~dm=\|\phi '\|_{L^1}$
. We consider a measurable map
$\mathrm {v}(\phi ):=\int _X |\phi '|~dm=\|\phi '\|_{L^1}$
. We consider a measurable map
![]() $T:\Omega \times X\to X$
such that
$T:\Omega \times X\to X$
such that
![]() $T_\omega :=T(\omega ,\cdot )$
is
$T_\omega :=T(\omega ,\cdot )$
is
![]() $C^r$
,
$C^r$
,
![]() $r\ge 2$
. In addition, we make the following assumptions.
$r\ge 2$
. In addition, we make the following assumptions.
-
• There exists a tempered random variable
 $N({\omega })$
so that (2.3) holds true.
$N({\omega })$
so that (2.3) holds true. -
• The map
 $\omega \in \Omega \mapsto (\int _X({|T_\omega "|}/{(T_\omega ')^2}) \,dm,\unicode{x3bb} _\omega )$
is measurable, where
$\omega \in \Omega \mapsto (\int _X({|T_\omega "|}/{(T_\omega ')^2}) \,dm,\unicode{x3bb} _\omega )$
is measurable, where
 $\unicode{x3bb} _\omega =\inf _{[0, 1]}|T_\omega '|$
.
$\unicode{x3bb} _\omega =\inf _{[0, 1]}|T_\omega '|$
. -
• The following expanding-on-average property holds:
(2.7)
-
• The map
 $\log (\int _X{|T_\omega "|}/{(T_\omega ')^2}\, dm)$
is
$\log (\int _X{|T_\omega "|}/{(T_\omega ')^2}\, dm)$
is
 $\mathbb P$
-integrable.
$\mathbb P$
-integrable. -
•
 .
.
We call a family
![]() $(T_\omega )_{\omega \in \Omega }$
satisfying the previous assumptions a smooth expanding-on-average cocycle. For a family
$(T_\omega )_{\omega \in \Omega }$
satisfying the previous assumptions a smooth expanding-on-average cocycle. For a family
![]() $(T_\omega )_{\omega \in \Omega }$
, countably valued and measurable, of smooth expanding-on-average cocycles which satisfy (2.3), the associated cocycle of transfer operators
$(T_\omega )_{\omega \in \Omega }$
, countably valued and measurable, of smooth expanding-on-average cocycles which satisfy (2.3), the associated cocycle of transfer operators
![]() $(\mathcal L_\omega )_{\omega \in \Omega }$
is good (see [Reference Dragičević and Sedro23, Example 16]). We note that our expansion-on-average condition (2.7) implies that
$(\mathcal L_\omega )_{\omega \in \Omega }$
is good (see [Reference Dragičević and Sedro23, Example 16]). We note that our expansion-on-average condition (2.7) implies that
![]() $\mathbb P$
-almost surely,
$\mathbb P$
-almost surely,
![]() $T_\omega $
has non-vanishing derivative, hence is a local diffeomorphism and a monotonic map of the circle. As noted in [Reference Dragičević, Hafouta and Sedro22, Example 6], smooth expanding-on-average cocycles satisfy a stronger version of the random covering property (which by [Reference Buzzi12, Remark 0.1] implies the one formulated in (2.6)): for each non-trivial interval
$T_\omega $
has non-vanishing derivative, hence is a local diffeomorphism and a monotonic map of the circle. As noted in [Reference Dragičević, Hafouta and Sedro22, Example 6], smooth expanding-on-average cocycles satisfy a stronger version of the random covering property (which by [Reference Buzzi12, Remark 0.1] implies the one formulated in (2.6)): for each non-trivial interval
![]() $I\subset X$
, for
$I\subset X$
, for
![]() $\mathbb P$
-a.e.
$\mathbb P$
-a.e.
![]() $\omega \in \Omega $
, there is an
$\omega \in \Omega $
, there is an
![]() $n_c:=n_c(\omega ,I)<\infty $
such that, for all
$n_c:=n_c(\omega ,I)<\infty $
such that, for all
![]() $n\ge n_c$
,
$n\ge n_c$
,
2.2 The one-dimensionality of the top Oseledets space: a summary of known results
In this section we recall two results from [Reference Dragičević, Hafouta and Sedro22] that will be in constant use in the course of the proofs of all of our results.
Theorem 2.8. [Reference Dragičević, Hafouta and Sedro22, Theorem 12]
Let
![]() $\mathcal L=(\mathcal L_\omega )_{\omega \in \Omega }$
be a good cocycle of transfer operators. Then the following assertions hold.
$\mathcal L=(\mathcal L_\omega )_{\omega \in \Omega }$
be a good cocycle of transfer operators. Then the following assertions hold.
-
• There exists an essentially unique measurable family
 $(h_\omega )_{\omega \in \Omega }\subset BV$
such that
$(h_\omega )_{\omega \in \Omega }\subset BV$
such that
 $h_\omega \ge 0$
,
$h_\omega \ge 0$
,
 $\int _X h_\omega \, dm=1$
and
$\int _X h_\omega \, dm=1$
and  $$ \begin{align*} \mathcal L_\omega h_\omega=h_{\sigma \omega} \quad \text{for }{\mathbb P}\text{-a.e. }\omega \in \Omega. \end{align*} $$
$$ \begin{align*} \mathcal L_\omega h_\omega=h_{\sigma \omega} \quad \text{for }{\mathbb P}\text{-a.e. }\omega \in \Omega. \end{align*} $$
-
• There is a random variable
 $\ell :\Omega \to (0,+\infty )$
such that, for
$\ell :\Omega \to (0,+\infty )$
such that, for
 $\mathbb P$
-a.e.
$\mathbb P$
-a.e.
 $\omega \in \Omega $
, (2.8)
$\omega \in \Omega $
, (2.8) $$ \begin{align} h_\omega \ge \ell(\omega), \quad m\text{-a.e.} \end{align} $$
$$ \begin{align} h_\omega \ge \ell(\omega), \quad m\text{-a.e.} \end{align} $$
-
• For
 $\mathbb P$
-a.e.
$\mathbb P$
-a.e.
 $\omega \in \Omega $
, (2.9)where
$\omega \in \Omega $
, (2.9)where $$ \begin{align} BV=\mathrm{span}\{h_\omega\} \oplus BV^0, \end{align} $$
$$ \begin{align} BV=\mathrm{span}\{h_\omega\} \oplus BV^0, \end{align} $$
 $$ \begin{align*} BV^0=\bigg \{ h\in BV: \int_X h\, dm=0 \bigg \}. \end{align*} $$
$$ \begin{align*} BV^0=\bigg \{ h\in BV: \int_X h\, dm=0 \bigg \}. \end{align*} $$
-
•
 $\omega \mapsto \|h_\omega \|_{BV}$
is tempered.
$\omega \mapsto \|h_\omega \|_{BV}$
is tempered. -
• There exist
 $\unicode{x3bb}>0$
and for each
$\unicode{x3bb}>0$
and for each
 $\epsilon>0$
, a tempered random variable
$\epsilon>0$
, a tempered random variable
 $D=D_\epsilon \colon \Omega \to (0, +\infty )$
such that, for
$D=D_\epsilon \colon \Omega \to (0, +\infty )$
such that, for
 $\mathbb P$
-a.e.
$\mathbb P$
-a.e.
 $\omega \in \Omega $
and
$\omega \in \Omega $
and
 $n\in \mathbb N$
, (2.10)and
$n\in \mathbb N$
, (2.10)and $$ \begin{align} \| \mathcal L_\omega^n \Pi(\omega) \|_{BV} \le D(\omega)e^{-\unicode{x3bb} n} \end{align} $$
(2.11)where
$$ \begin{align} \| \mathcal L_\omega^n \Pi(\omega) \|_{BV} \le D(\omega)e^{-\unicode{x3bb} n} \end{align} $$
(2.11)where $$ \begin{align} \| \mathcal L_\omega^n(\mathrm{Id}- \Pi(\omega)) \|_{BV} \le D(\omega)e^{\epsilon n}, \end{align} $$
$$ \begin{align} \| \mathcal L_\omega^n(\mathrm{Id}- \Pi(\omega)) \|_{BV} \le D(\omega)e^{\epsilon n}, \end{align} $$
 $\Pi (\omega ) \colon BV \to BV^0$
is a projection associated to the splitting (2.9).
$\Pi (\omega ) \colon BV \to BV^0$
is a projection associated to the splitting (2.9).
Finally, for uniformly random cocycles the random variables
 $\ell ({\omega })$
and
$\ell ({\omega })$
and
 $D({\omega })$
can be replaced with positive constants and
$D({\omega })$
can be replaced with positive constants and
 ${\omega }\to \|h_{\omega }\|_{BV}$
is a bounded random variable.
${\omega }\to \|h_{\omega }\|_{BV}$
is a bounded random variable.
Corollary 2.9. [Reference Dragičević, Hafouta and Sedro22, Corollary 13]
Let
![]() $\mathcal L=(\mathcal L_\omega )_{\omega \in \Omega }$
be a good cocycle of transfer operators. Then the following assertions hold.
$\mathcal L=(\mathcal L_\omega )_{\omega \in \Omega }$
be a good cocycle of transfer operators. Then the following assertions hold.
-
• If
 $(h_\omega )_{\omega \in \Omega }\subset BV$
is given by Theorem 2.8, then (2.12)
$(h_\omega )_{\omega \in \Omega }\subset BV$
is given by Theorem 2.8, then (2.12) $$ \begin{align} \omega \mapsto \| 1/h_\omega\|_{BV} \ \text{is tempered.} \end{align} $$
$$ \begin{align} \omega \mapsto \| 1/h_\omega\|_{BV} \ \text{is tempered.} \end{align} $$
-
• For
 $\mathbb P$
-a.e.
$\mathbb P$
-a.e.
 $\omega \in \Omega $
, (2.13)where
$\omega \in \Omega $
, (2.13)where in which
in which $$ \begin{align*} BV_\omega^0=\bigg \{ h\in BV: \int_X h\, d\mu_\omega=0 \bigg \}, \end{align*} $$
$$ \begin{align*} BV_\omega^0=\bigg \{ h\in BV: \int_X h\, d\mu_\omega=0 \bigg \}, \end{align*} $$
 $d\mu _\omega =h_\omega dm$
,
$d\mu _\omega =h_\omega dm$
,
 $\omega \in \Omega $
;
$\omega \in \Omega $
;
-
• there exist
 $\unicode{x3bb} '>0$
and a tempered random variable
$\unicode{x3bb} '>0$
and a tempered random variable
 $\tilde D\colon \Omega \to (0, +\infty )$
such that, for
$\tilde D\colon \Omega \to (0, +\infty )$
such that, for
 $\mathbb P$
-a.e.
$\mathbb P$
-a.e.
 $\omega \in \Omega $
and
$\omega \in \Omega $
and
 $n\in \mathbb N$
, (2.14)
$n\in \mathbb N$
, (2.14) $$ \begin{align} \| L_\omega^n \tilde \Pi(\omega) \|_{BV} \le \tilde D(\omega)e^{-\unicode{x3bb}' n}, \end{align} $$
(2.15)where
$$ \begin{align} \| L_\omega^n \tilde \Pi(\omega) \|_{BV} \le \tilde D(\omega)e^{-\unicode{x3bb}' n}, \end{align} $$
(2.15)where $$ \begin{align} \| L_\omega^n(\mathrm{Id}- \tilde \Pi(\omega)) \|_{BV} \le \tilde D(\omega), \end{align} $$
$$ \begin{align} \| L_\omega^n(\mathrm{Id}- \tilde \Pi(\omega)) \|_{BV} \le \tilde D(\omega), \end{align} $$
 $\tilde \Pi (\omega ) \colon BV \to BV_\omega ^0$
is a projection associated to the splitting (2.13), and
$\tilde \Pi (\omega ) \colon BV \to BV_\omega ^0$
is a projection associated to the splitting (2.13), and  $$ \begin{align*} L_\omega^n g =\mathcal L_\omega^n(g h_\omega) /h_{\sigma^n \omega}, \quad g\in BV, \ n\in \mathbb N. \end{align*} $$
$$ \begin{align*} L_\omega^n g =\mathcal L_\omega^n(g h_\omega) /h_{\sigma^n \omega}, \quad g\in BV, \ n\in \mathbb N. \end{align*} $$
Finally, for uniformly random cocycles the random variable
 $\tilde D({\omega })$
can be replaced with a positive constant.
$\tilde D({\omega })$
can be replaced with a positive constant.
Since
![]() ${\mathcal L}_{\omega } h_{\omega }=h_{\sigma {\omega }}$
and
${\mathcal L}_{\omega } h_{\omega }=h_{\sigma {\omega }}$
and
![]() ${\mathcal L}_{\omega }$
satisfy the duality relation (2.2), the measure
${\mathcal L}_{\omega }$
satisfy the duality relation (2.2), the measure
![]() $\mu _{\omega }$
satisfies that for
$\mu _{\omega }$
satisfies that for
![]() ${\mathbb P}$
-a.e.
${\mathbb P}$
-a.e.
![]() ${\omega }$
we have
${\omega }$
we have
![]() $(T_{\omega })_*\mu _{\omega }=\mu _{{\sigma }_{\omega }}$
. Thus, if
$(T_{\omega })_*\mu _{\omega }=\mu _{{\sigma }_{\omega }}$
. Thus, if
![]() $\tau :{\Omega }\times X\to {\Omega }\times X$
is defined by
$\tau :{\Omega }\times X\to {\Omega }\times X$
is defined by
![]() $\tau ({\omega },x)=({\sigma }{\omega },T_{\omega } x)$
then
$\tau ({\omega },x)=({\sigma }{\omega },T_{\omega } x)$
then
![]() $\mu _{\omega }$
gives rise to a
$\mu _{\omega }$
gives rise to a
![]() $\tau $
-invariant probability measure
$\tau $
-invariant probability measure
![]() $\mu $
on
$\mu $
on
![]() ${\Omega }\times X$
such that
${\Omega }\times X$
such that
for every measurable set A in
![]() ${\Omega }$
and B in X, where
${\Omega }$
and B in X, where
![]() $h({\omega },x)=h_{\omega }(x)$
.
$h({\omega },x)=h_{\omega }(x)$
.
2.3 Main results: limit theorems for mixing base maps
2.4 The observable
Let us take a measurable
![]() $\varphi :{\Omega }\times X\to {\mathbb R}$
so that
$\varphi :{\Omega }\times X\to {\mathbb R}$
so that
![]() $\int \varphi\, d\mu =0$
. Let
$\int \varphi\, d\mu =0$
. Let
![]() $\tilde K({\omega })$
be the tempered random variable defined by
$\tilde K({\omega })$
be the tempered random variable defined by
where
![]() $D({\omega }),\tilde D({\omega })$
and
$D({\omega }),\tilde D({\omega })$
and
![]() $N({\omega })$
are specified in the definition of a good cocycles and in Theorem 2.8 and Corollary 2.9. In order to describe our assumptions on the observable
$N({\omega })$
are specified in the definition of a good cocycles and in Theorem 2.8 and Corollary 2.9. In order to describe our assumptions on the observable
![]() $\varphi $
, we will need the following classical result (see [Reference Arnold4, Proposition 4.3.3.]).
$\varphi $
, we will need the following classical result (see [Reference Arnold4, Proposition 4.3.3.]).
Proposition 2.10. Let
![]() $\tilde K \colon \Omega \to (0, +\infty )$
be a tempered random variable. For each
$\tilde K \colon \Omega \to (0, +\infty )$
be a tempered random variable. For each
![]() $\epsilon>0$
, there exists a tempered random variable
$\epsilon>0$
, there exists a tempered random variable
![]() $\tilde K_\epsilon \colon \Omega \to (1, +\infty )$
such that
$\tilde K_\epsilon \colon \Omega \to (1, +\infty )$
such that
 $$ \begin{align*} \frac{1}{\tilde K_\epsilon (\omega)} \le \tilde K(\omega) \le \tilde K_\epsilon (\omega) \quad \text{and} \quad \tilde K_\epsilon(\omega)e^{-\epsilon |n|} \le \tilde K_\epsilon (\sigma^n \omega) \le \tilde K_\epsilon (\omega) e^{\epsilon |n|}, \end{align*} $$
$$ \begin{align*} \frac{1}{\tilde K_\epsilon (\omega)} \le \tilde K(\omega) \le \tilde K_\epsilon (\omega) \quad \text{and} \quad \tilde K_\epsilon(\omega)e^{-\epsilon |n|} \le \tilde K_\epsilon (\sigma^n \omega) \le \tilde K_\epsilon (\omega) e^{\epsilon |n|}, \end{align*} $$
for
![]() $\mathbb P$
-a.e.
$\mathbb P$
-a.e.
![]() $\omega \in \Omega $
and
$\omega \in \Omega $
and
![]() $n \in \mathbb Z$
.
$n \in \mathbb Z$
.
Next, using the notation of Proposition 2.10, let
![]() $K({\omega })=\tilde K_{\varepsilon }({\omega })$
for some
$K({\omega })=\tilde K_{\varepsilon }({\omega })$
for some
![]() ${\varepsilon }<{\unicode{x3bb} }"/3$
, where
${\varepsilon }<{\unicode{x3bb} }"/3$
, where
![]() ${\unicode{x3bb} }"=\min ({\unicode{x3bb} },{\unicode{x3bb} }')$
, and
${\unicode{x3bb} }"=\min ({\unicode{x3bb} },{\unicode{x3bb} }')$
, and
![]() ${\unicode{x3bb} }$
and
${\unicode{x3bb} }$
and
![]() ${\unicode{x3bb} }'$
are specified in Theorem 2.8 and Corollary 2.9, respectively.
${\unicode{x3bb} }'$
are specified in Theorem 2.8 and Corollary 2.9, respectively.
Remark 2.11. From now on we will replace both
![]() ${\unicode{x3bb} }$
and
${\unicode{x3bb} }$
and
![]() ${\unicode{x3bb} }'$
by their minimum, which for notational convenience will be denoted by
${\unicode{x3bb} }'$
by their minimum, which for notational convenience will be denoted by
![]() ${\unicode{x3bb} }$
.
${\unicode{x3bb} }$
.
In what follows we will consider an observable
![]() $\varphi :{\Omega }\times X\to {\mathbb R}$
satisfying the scaling condition
$\varphi :{\Omega }\times X\to {\mathbb R}$
satisfying the scaling condition
which was first introduced in [Reference Dragičević and Sedro23]. In the uniformly random case
![]() $\tilde K({\omega })$
(and hence
$\tilde K({\omega })$
(and hence
![]() $K({\omega })$
) can be replace by a positive constant, and so the scaling condition reads
$K({\omega })$
) can be replace by a positive constant, and so the scaling condition reads
The main goal in this paper is to obtain limit theorems for the sequence of functions
 $$ \begin{align*} S_n=S_n\varphi=\sum_{j=0}^{n-1}\varphi\circ \tau^j \end{align*} $$
$$ \begin{align*} S_n=S_n\varphi=\sum_{j=0}^{n-1}\varphi\circ \tau^j \end{align*} $$
under certain mixing assumptions on the driving system
![]() $({\Omega },{\mathcal F},{\mathbb P},\sigma )$
and the above assumptions on the observable
$({\Omega },{\mathcal F},{\mathbb P},\sigma )$
and the above assumptions on the observable
![]() $\varphi $
.
$\varphi $
.
Remark 2.12. For expanding-on-average maps the scaling condition (2.16) is necessary for limit theorems (see [Reference Dragičević, Hafouta and Sedro22, Appendix]). In any case, our results are also new in the uniformly random case, and readers who would prefer can just consider this case together with the assumption that
![]() $\operatorname {\mathrm {esssup}}_{{\omega }\in {\Omega }}\|\varphi _{\omega }\|_{BV}<\infty $
.
$\operatorname {\mathrm {esssup}}_{{\omega }\in {\Omega }}\|\varphi _{\omega }\|_{BV}<\infty $
.
Let us also note that, in general, the random variable
![]() $K({\omega })$
comes from Oseledets theorem and it is not computable. In order to provide explicit conditions for quenched limit theorems, in [Reference Hafouta28] several examples of non-uniformly expanding maps (which are stronger than expansion on average) were given with the property that
$K({\omega })$
comes from Oseledets theorem and it is not computable. In order to provide explicit conditions for quenched limit theorems, in [Reference Hafouta28] several examples of non-uniformly expanding maps (which are stronger than expansion on average) were given with the property that
 $$ \begin{align} \|L_{\omega}^n-\mu_{\omega}\|_{BV}\leq B({\sigma}^n{\omega})\prod_{j=0}^{n-1}\rho({\sigma}^j{\omega}). \end{align} $$
$$ \begin{align} \|L_{\omega}^n-\mu_{\omega}\|_{BV}\leq B({\sigma}^n{\omega})\prod_{j=0}^{n-1}\rho({\sigma}^j{\omega}). \end{align} $$
Here the
![]() $BV$
norm is with respect to the choice of variation
$BV$
norm is with respect to the choice of variation
![]() $v(g)=v_{\alpha }(g)$
, where
$v(g)=v_{\alpha }(g)$
, where
![]() $v_{\alpha }$
is the Hölder constant corresponding to some exponent
$v_{\alpha }$
is the Hölder constant corresponding to some exponent
![]() ${\alpha }$
and
${\alpha }$
and
![]() $B({\omega })$
and
$B({\omega })$
and
![]() $\rho ({\omega })\in (0,1)$
are random variables with explicit formulas, and they depend only on the zeroth coordinate
$\rho ({\omega })\in (0,1)$
are random variables with explicit formulas, and they depend only on the zeroth coordinate
![]() ${\omega }_0$
. Moreover, for several of these examples we already have
${\omega }_0$
. Moreover, for several of these examples we already have
![]() $B({\omega })\leq B$
for some constant B. In this case (similarly to [Reference Dragičević, Hafouta and Sedro22, §5.2]) we have the following assertions. Let
$B({\omega })\leq B$
for some constant B. In this case (similarly to [Reference Dragičević, Hafouta and Sedro22, §5.2]) we have the following assertions. Let
![]() ${\varepsilon }$
be smaller than
${\varepsilon }$
be smaller than
![]() $1-{\mathbb E}_{\mathbb P}[\rho ]$
and let
$1-{\mathbb E}_{\mathbb P}[\rho ]$
and let
![]() $A=\{{\omega }: \rho ({\omega })\leq 1-{\varepsilon }\}$
. Then
$A=\{{\omega }: \rho ({\omega })\leq 1-{\varepsilon }\}$
. Then
![]() ${\mathbb P}(A)>0$
. Let
${\mathbb P}(A)>0$
. Let
![]() ${R_n({\omega })=\sum _{j=0}^{n-1}{\mathbb I}({\sigma }^j{\omega }\in A)}$
. Then
${R_n({\omega })=\sum _{j=0}^{n-1}{\mathbb I}({\sigma }^j{\omega }\in A)}$
. Then
![]() $R_n/n\to r={\mathbb P}(A)$
(
$R_n/n\to r={\mathbb P}(A)$
(
![]() ${\mathbb P}$
-almost surely). Let
${\mathbb P}$
-almost surely). Let
Then, for
![]() $\mathbb P$
-a.e.
$\mathbb P$
-a.e.
![]() $\omega \in \Omega $
and
$\omega \in \Omega $
and
![]() $n\in {\mathbb N}$
,
$n\in {\mathbb N}$
,
where
![]() $K(\omega )=B(1-{\varepsilon })^{N(\omega )}$
. Observe that for
$K(\omega )=B(1-{\varepsilon })^{N(\omega )}$
. Observe that for
![]() $k\ge 1$
,
$k\ge 1$
,
 $$ \begin{align*}\{N(\omega)=k+1\}\subset \bigg\{\bigg|\frac{R_{k}(\omega)}{k}-r\bigg|>\frac 1 2 r\bigg\}.\end{align*} $$
$$ \begin{align*}\{N(\omega)=k+1\}\subset \bigg\{\bigg|\frac{R_{k}(\omega)}{k}-r\bigg|>\frac 1 2 r\bigg\}.\end{align*} $$
Thus, if the stationary process
![]() $(\mathbb I_A\circ \sigma ^n)$
satisfies an appropriate concentration inequality (for example, under appropriate mixing assumptions on
$(\mathbb I_A\circ \sigma ^n)$
satisfies an appropriate concentration inequality (for example, under appropriate mixing assumptions on
![]() $(\xi _n)$
), we can conclude that
$(\xi _n)$
), we can conclude that
![]() $N(\omega )$
is integrable. Hence,
$N(\omega )$
is integrable. Hence,
![]() $\log K$
is integrable and consequently also tempered.
$\log K$
is integrable and consequently also tempered.
The above means that in this situation we can express the condition on
![]() $\varphi $
by means of the more explicit random variable
$\varphi $
by means of the more explicit random variable
![]() $K({\omega })$
defined above. Still, in the setup of [Reference Hafouta28], under appropriate integrability conditions on
$K({\omega })$
defined above. Still, in the setup of [Reference Hafouta28], under appropriate integrability conditions on
![]() $B({\omega })$
the main results in this paper can be obtained under conditions such as
$B({\omega })$
the main results in this paper can be obtained under conditions such as
![]() $\varphi \in L^p(\mu )$
for p large enough (depending on the desired result). Since this approach requires several non-trivial modifications to the arguments in this paper such results will be considered elsewhere.
$\varphi \in L^p(\mu )$
for p large enough (depending on the desired result). Since this approach requires several non-trivial modifications to the arguments in this paper such results will be considered elsewhere.
2.5 Limit theorems
Let us first introduce our assumptions on the base map. Let
![]() $(\xi _n)$
be a two-sided stationary sequence taking values on some measurable space
$(\xi _n)$
be a two-sided stationary sequence taking values on some measurable space
![]() ${\mathcal Y}$
. We assume here that
${\mathcal Y}$
. We assume here that
![]() $({\Omega },{\mathcal F},{\mathbb P},\sigma )$
is the corresponding shift system. Namely,
$({\Omega },{\mathcal F},{\mathbb P},\sigma )$
is the corresponding shift system. Namely,
![]() $\Omega ={\mathcal Y}^{\mathbb Z}$
,
$\Omega ={\mathcal Y}^{\mathbb Z}$
,
![]() $({\sigma } {\omega })_j=({\omega }_{j+1})_j$
is the left shift and if
$({\sigma } {\omega })_j=({\omega }_{j+1})_j$
is the left shift and if
![]() $\pi _0:\Omega \to {\mathcal Y}$
denotes the zeroth coordinate projection, then
$\pi _0:\Omega \to {\mathcal Y}$
denotes the zeroth coordinate projection, then
![]() $(\xi _n)$
has the same distribution as
$(\xi _n)$
has the same distribution as
![]() $(\pi _0\circ \sigma ^n)$
. We also assume that
$(\pi _0\circ \sigma ^n)$
. We also assume that
![]() $T_{\omega }=T_{{\omega }_0}$
and
$T_{\omega }=T_{{\omega }_0}$
and
![]() $\varphi ({\omega },\cdot )=\varphi ({\omega }_0,\cdot )$
depend only on zeroth coordinate
$\varphi ({\omega },\cdot )=\varphi ({\omega }_0,\cdot )$
depend only on zeroth coordinate
![]() ${\omega }_0$
of
${\omega }_0$
of
![]() ${\omega }$
.
${\omega }$
.
2.5.1 Limit theorems for stretched exponentially fast
 $\alpha $
-mixing driving processes
$\alpha $
-mixing driving processes
Let
![]() $({\Omega }_0,\mathscr F,\textbf {P})$
be the probability space on which
$({\Omega }_0,\mathscr F,\textbf {P})$
be the probability space on which
![]() $(\xi _n)$
is defined. We recall that the
$(\xi _n)$
is defined. We recall that the
![]() ${\alpha }$
-mixing (dependence) coefficient between two sub-
${\alpha }$
-mixing (dependence) coefficient between two sub-
![]() ${\sigma }$
-algebras
${\sigma }$
-algebras
![]() ${\mathcal G},{\mathcal H}$
of
${\mathcal G},{\mathcal H}$
of
![]() $\mathscr F$
is given by
$\mathscr F$
is given by
The
![]() ${\alpha }$
-dependence coefficients of
${\alpha }$
-dependence coefficients of
![]() $(\xi _n)$
are defined by
$(\xi _n)$
are defined by
where
![]() $\mathscr F_{-\infty ,k}$
is the
$\mathscr F_{-\infty ,k}$
is the
![]() $\sigma $
-algebra generated by
$\sigma $
-algebra generated by
![]() $\xi _j$
,
$\xi _j$
,
![]() $j\leq k$
, and
$j\leq k$
, and
![]() $\mathscr F_{k+n,\infty }$
is generated by
$\mathscr F_{k+n,\infty }$
is generated by
![]() ${\xi _j, j\geq k+n}$
. The last equality holds true due to stationarity. Let us consider the following class of mixing assumptions on the base map.
${\xi _j, j\geq k+n}$
. The last equality holds true due to stationarity. Let us consider the following class of mixing assumptions on the base map.
Assumption 2.13. (Stretched exponential
 $\alpha $
mixing rates)
$\alpha $
mixing rates)
There exist positive constants
![]() $c_1,c_2$
and
$c_1,c_2$
and
![]() $\eta $
such that
$\eta $
such that
![]() ${\alpha }_n\leq c_1e^{-c_2n^\eta }$
for every n.
${\alpha }_n\leq c_1e^{-c_2n^\eta }$
for every n.
Our first result concerns the variance of
![]() $S_n$
and the CLT (with rates).
$S_n$
and the CLT (with rates).
Theorem 2.14. Suppose that the cocycle
![]() ${\mathcal L}$
is good. Let
${\mathcal L}$
is good. Let
![]() $\varphi $
be an observable such that
$\varphi $
be an observable such that
![]() $\|\varphi \|_K:=\operatorname {\mathrm {esssup}}_{{\omega }\in {\Omega }}(K({\omega })\|\varphi _{\omega }\|_{BV})<\infty $
, where
$\|\varphi \|_K:=\operatorname {\mathrm {esssup}}_{{\omega }\in {\Omega }}(K({\omega })\|\varphi _{\omega }\|_{BV})<\infty $
, where
![]() $\varphi _{\omega }=\varphi ({\omega },\cdot )$
. Suppose that
$\varphi _{\omega }=\varphi ({\omega },\cdot )$
. Suppose that
![]() ${\sum _n n{\alpha }_n<\infty }$
. Then the limit
${\sum _n n{\alpha }_n<\infty }$
. Then the limit
exists and vanishes if and only if
![]() $\varphi =r\circ \tau -r$
for some
$\varphi =r\circ \tau -r$
for some
![]() $r\in L^2(\mu )$
. If in addition Assumption 2.13 is satisfied then
$r\in L^2(\mu )$
. If in addition Assumption 2.13 is satisfied then
![]() $n^{-1/2}S_n$
converges in distribution to
$n^{-1/2}S_n$
converges in distribution to
![]() $sZ$
, where Z is a standard normal random variable. Moreover, there is a constant
$sZ$
, where Z is a standard normal random variable. Moreover, there is a constant
![]() $C>0$
such that. for all
$C>0$
such that. for all
![]() $n\in {\mathbb N}$
,
$n\in {\mathbb N}$
,
where
![]() $\gamma =1/\eta $
and
$\gamma =1/\eta $
and
![]() $\Phi $
is the standard normal distribution function. The constant C depends only on
$\Phi $
is the standard normal distribution function. The constant C depends only on
![]() $c_1,c_2,\eta $
,
$c_1,c_2,\eta $
,
![]() $\|\varphi \|_K$
and the constant
$\|\varphi \|_K$
and the constant
![]() $C_{\mathrm {v}}$
(from the definition of the variation
$C_{\mathrm {v}}$
(from the definition of the variation
![]() $\mathrm {v}(\cdot )$
), and an explicit formula for C can be recovered from the proof.
$\mathrm {v}(\cdot )$
), and an explicit formula for C can be recovered from the proof.
The proof of Theorem 2.14 appears in §3.2.1. As discussed in §§1.2 and 1.3, when the quenched CLT holds true with a deterministic centering, then the CLT for the skew product follows by integration. This was the approach for the CLT in [Reference Aimino, Nicol and Vaienti2], but in the setup of this paper the function
![]() $\varphi $
and the measure
$\varphi $
and the measure
![]() $\mu _{\omega }$
depend on
$\mu _{\omega }$
depend on
![]() ${\omega }$
, and so the quenched CLT only holds with fiberwise centering. Thus, the novelty of Theorem 2.14 is that the CLT is obtained for the skew product beyond the annealed case considered in [Reference Aimino, Nicol and Vaienti2]. Moreover, Theorem 2.19 also strengthens the CLT in [Reference Hafouta26], since our maps
${\omega }$
, and so the quenched CLT only holds with fiberwise centering. Thus, the novelty of Theorem 2.14 is that the CLT is obtained for the skew product beyond the annealed case considered in [Reference Aimino, Nicol and Vaienti2]. Moreover, Theorem 2.19 also strengthens the CLT in [Reference Hafouta26], since our maps
![]() $T_{\omega }$
are not uniformly expanding, and the observable
$T_{\omega }$
are not uniformly expanding, and the observable
![]() $\varphi $
is not fiberwise centered.
$\varphi $
is not fiberwise centered.
Next, let us discuss our results concerning moderate-deviations and exponential concentration inequalities.
Theorem 2.15. Suppose that the cocycle
![]() ${\mathcal L}$
is good, and let
${\mathcal L}$
is good, and let
![]() $\varphi $
be an observable so that
$\varphi $
be an observable so that
![]() $\|\varphi \|_K=\operatorname {\mathrm {esssup}}_{{\omega }\in {\Omega }}(K({\omega })\|\varphi _{\omega }\|_{BV})<\infty $
. Let Assumption 2.13 hold and set
$\|\varphi \|_K=\operatorname {\mathrm {esssup}}_{{\omega }\in {\Omega }}(K({\omega })\|\varphi _{\omega }\|_{BV})<\infty $
. Let Assumption 2.13 hold and set
![]() ${\gamma }=1/\eta $
. Then there exist constants
${\gamma }=1/\eta $
. Then there exist constants
![]() $a_1,a_2>0$
such that, for every
$a_1,a_2>0$
such that, for every
![]() $x>0$
and
$x>0$
and
![]() $n\in {\mathbb N}$
,
$n\in {\mathbb N}$
,
 $$ \begin{align} \mu(|S_n-{\mathbb E}[S_n]|\geq x)\leq 2\exp\bigg(-\frac{x^2}{2(a_1+a_2xn^{-1/({2+4{\gamma}})})^{({1+2{\gamma}})/({1+{\gamma}})}}\bigg). \end{align} $$
$$ \begin{align} \mu(|S_n-{\mathbb E}[S_n]|\geq x)\leq 2\exp\bigg(-\frac{x^2}{2(a_1+a_2xn^{-1/({2+4{\gamma}})})^{({1+2{\gamma}})/({1+{\gamma}})}}\bigg). \end{align} $$
All the constants depend only on
![]() $c_1,c_2,\eta $
,
$c_1,c_2,\eta $
,
![]() $\|\varphi \|_K$
and
$\|\varphi \|_K$
and
![]() $C_{\mathrm {v}}$
from the definition of the variation
$C_{\mathrm {v}}$
from the definition of the variation
![]() $\mathrm {v}(\cdot )$
, and an explicit formula for them can be recovered from the proof.
$\mathrm {v}(\cdot )$
, and an explicit formula for them can be recovered from the proof.
We will also prove the following theorem.
Theorem 2.16. Suppose that the cocycle
![]() ${\mathcal L}$
is good, and let
${\mathcal L}$
is good, and let
![]() $\varphi $
be an observable such that
$\varphi $
be an observable such that
![]() $\|\varphi \|_K=\operatorname {\mathrm {esssup}}_{{\omega }\in {\Omega }}(K({\omega })\|\varphi _{\omega }\|_{BV})<\infty $
. Let Assumption 2.13 hold and set
$\|\varphi \|_K=\operatorname {\mathrm {esssup}}_{{\omega }\in {\Omega }}(K({\omega })\|\varphi _{\omega }\|_{BV})<\infty $
. Let Assumption 2.13 hold and set
![]() ${\gamma }=1/\eta $
. Let us also assume that the asymptotic variance
${\gamma }=1/\eta $
. Let us also assume that the asymptotic variance
![]() $s^2$
is positive.
$s^2$
is positive.
(i) Set
![]() $v_n=\sqrt {\mathrm {Var}(S_n)}$
, and when
$v_n=\sqrt {\mathrm {Var}(S_n)}$
, and when
![]() $v_n>0$
also set
$v_n>0$
also set
![]() $Z_n=({S_n-{\mathbb E}[S_n]})/{v_n}$
. Let
$Z_n=({S_n-{\mathbb E}[S_n]})/{v_n}$
. Let
![]() $\Phi $
be the standard normal distribution function. Then there exist constants
$\Phi $
be the standard normal distribution function. Then there exist constants
![]() $s_3,s_4,s_5>0$
such that, that for every
$s_3,s_4,s_5>0$
such that, that for every
![]() $n\geq a_3$
we have
$n\geq a_3$
we have
![]() $v_n>0$
, and for every
$v_n>0$
, and for every
![]() $0\leq x<a_4 n^{1/({2+4{\gamma }})}$
,
$0\leq x<a_4 n^{1/({2+4{\gamma }})}$
,
 $$ \begin{align} \begin{aligned}\bigg|\ln\frac{\mu(Z_n\geq x)}{1-\Phi(x)}\bigg|\leq a_5(1+x^3) n^{-1/({2+4{\gamma}})}\,\,\text{ and}\\ \bigg|\ln\frac{\mu(Z_n\leq -x)}{\Phi(-x)}\bigg|\leq a_5(1+x^3) n^{-1/({2+4{\gamma}})}.\end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned}\bigg|\ln\frac{\mu(Z_n\geq x)}{1-\Phi(x)}\bigg|\leq a_5(1+x^3) n^{-1/({2+4{\gamma}})}\,\,\text{ and}\\ \bigg|\ln\frac{\mu(Z_n\leq -x)}{\Phi(-x)}\bigg|\leq a_5(1+x^3) n^{-1/({2+4{\gamma}})}.\end{aligned} \end{align} $$
The constants
![]() $a_4,a_5$
depend only on
$a_4,a_5$
depend only on
![]() $c_1,c_2,\eta $
,
$c_1,c_2,\eta $
,
![]() $\|\varphi \|_K$
and
$\|\varphi \|_K$
and
![]() $C_{\mathrm {v}}$
, and an explicit formula for them can be recovered from the proof.
$C_{\mathrm {v}}$
, and an explicit formula for them can be recovered from the proof.
(ii) Let
![]() $a_n$
,
$a_n$
,
![]() $n\geq 1$
, be a sequence of real numbers so that
$n\geq 1$
, be a sequence of real numbers so that
Then the sequence
![]() $W_n=(sn^{1/2}a_n)^{-1}S_n$
,
$W_n=(sn^{1/2}a_n)^{-1}S_n$
,
![]() $n\geq 1$
, satisfies the moderate-deviations principle with speed
$n\geq 1$
, satisfies the moderate-deviations principle with speed
![]() $s_n=a_n^2$
and the rate function
$s_n=a_n^2$
and the rate function
![]() $I(x)={x^2}/2$
. Namely, for every Borel measurable set
$I(x)={x^2}/2$
. Namely, for every Borel measurable set
![]() $\Gamma \subset {\mathbb R}$
,
$\Gamma \subset {\mathbb R}$
,
 $$ \begin{align*} -\inf_{x\in\Gamma^o}I(x)\leq \liminf_{n\to\infty}\frac 1{a_n^2}\ln\mu(W_n\in\Gamma)\leq \limsup_{n\to\infty}\frac 1{a_n^2}\ln\mu(W_n\in\Gamma)\leq -\inf_{x\in\overline{\Gamma}}I(x) \end{align*} $$
$$ \begin{align*} -\inf_{x\in\Gamma^o}I(x)\leq \liminf_{n\to\infty}\frac 1{a_n^2}\ln\mu(W_n\in\Gamma)\leq \limsup_{n\to\infty}\frac 1{a_n^2}\ln\mu(W_n\in\Gamma)\leq -\inf_{x\in\overline{\Gamma}}I(x) \end{align*} $$
where
![]() $\Gamma ^o$
is the interior of
$\Gamma ^o$
is the interior of
![]() $\Gamma $
and
$\Gamma $
and
![]() $\overline {\Gamma }$
is its closure.
$\overline {\Gamma }$
is its closure.
We also obtain the following Rosenthal-type moment estimates.
Theorem 2.17. Suppose that
![]() ${\mathcal L}$
is a good cocycle. If
${\mathcal L}$
is a good cocycle. If
![]() $\|\varphi \|_K\kern1pt{=}\kern1pt\operatorname {\mathrm {esssup}}_{{\omega }\in {\Omega }}(K({\omega })\|\varphi _{\omega }\|_{BV}) \kern1pt{<}\infty $
, then under Assumption 2.13 there exists a constant
$\|\varphi \|_K\kern1pt{=}\kern1pt\operatorname {\mathrm {esssup}}_{{\omega }\in {\Omega }}(K({\omega })\|\varphi _{\omega }\|_{BV}) \kern1pt{<}\infty $
, then under Assumption 2.13 there exists a constant
![]() $c_0$
such that, with
$c_0$
such that, with
![]() $\gamma =1/\eta $
for every integer
$\gamma =1/\eta $
for every integer
![]() $p\geq 1$
, we have
$p\geq 1$
, we have
 $$ \begin{align} &|{\mathbb E}_\mu[(S_n-{\mathbb E}_\mu[S_n])^p]-(\mathrm{Var}_\mu(S_n))^{p/2}{\mathbb E}[Z^p]|\nonumber\\&\quad\leq (c_{0})^p(p{!})^{1+{\gamma}}\sum_{1\leq u\leq ({p-1})/2}n^u\frac{p^u}{(u{!})^2}=O(n^{[(p-1)/2]}), \end{align} $$
$$ \begin{align} &|{\mathbb E}_\mu[(S_n-{\mathbb E}_\mu[S_n])^p]-(\mathrm{Var}_\mu(S_n))^{p/2}{\mathbb E}[Z^p]|\nonumber\\&\quad\leq (c_{0})^p(p{!})^{1+{\gamma}}\sum_{1\leq u\leq ({p-1})/2}n^u\frac{p^u}{(u{!})^2}=O(n^{[(p-1)/2]}), \end{align} $$
where Z is a standard normal random variable. In particular,
![]() $\|S_n-{\mathbb E}_\mu [S_n]\|_{L^p}=O(\sqrt n)$
for every p. As in the previous theorems, the constant
$\|S_n-{\mathbb E}_\mu [S_n]\|_{L^p}=O(\sqrt n)$
for every p. As in the previous theorems, the constant
![]() $c_0$
depends (explicitly) only on
$c_0$
depends (explicitly) only on
![]() $c_1,c_2,\eta $
,
$c_1,c_2,\eta $
,
![]() $\|\varphi \|_K$
and
$\|\varphi \|_K$
and
![]() $C_{\mathrm {v}}$
.
$C_{\mathrm {v}}$
.
We remark that Theorem 2.17 provides another proof of the CLT by the method of moments. Indeed, if
![]() $s^2>0$
then it follows that, for every integer
$s^2>0$
then it follows that, for every integer
![]() $p\geq 1$
, the pth moment of
$p\geq 1$
, the pth moment of
![]() $(S_n-{\mathbb E}[S_n])n^{-1/2}s^{-1}$
converges to
$(S_n-{\mathbb E}[S_n])n^{-1/2}s^{-1}$
converges to
![]() ${\mathbb E}[Z^p]$
, where
${\mathbb E}[Z^p]$
, where
![]() $s^2$
is the asymptotic variance. In fact, for even p we get the convergence rate
$s^2$
is the asymptotic variance. In fact, for even p we get the convergence rate
![]() $O(n^{-1/2})$
, while for odd p we get the rate
$O(n^{-1/2})$
, while for odd p we get the rate
![]() $O(n^{-1})$
.
$O(n^{-1})$
.
Remark 2.18. The proofs of Theorems 2.15–2.17 appear in §3.2.2.
Theorems 2.15–2.17 are well established for sufficiently fast mixing (in the probabilistic sense) sequences of random variables, where one of the most notable methods of proof is the so-called method of cumulants (see [Reference Saulis and Statulevicius49]). For random dynamical systems, a moderate-deviations principle was obtained in [Reference Dragičević and Hafouta19], using a random complex Perron–Frobenius theorem. In the setup of [Reference Aimino, Nicol and Vaienti2], annealed (local) large-deviations principles and exponential concentration inequalities were obtained for i.i.d. maps, and we expect that for independent maps the methods in [Reference Aimino, Nicol and Vaienti2] will yield results like Theorems 2.15–2.17 as well. The novelty in Theorems 2.15–2.17 is that we show how to apply the method of cumulants in the context of skew products with non-independent fiber maps, which results in concentration inequalities, moderate-deviations principles and Gaussian moment estimates beyond the annealed setup [Reference Aimino, Nicol and Vaienti2].
Finally, let us consider the random function
![]() ${\mathcal S}_n(t)=n^{-1/2}(S_{[nt]}-{\mathbb E}[S_{nt}])$
on
${\mathcal S}_n(t)=n^{-1/2}(S_{[nt]}-{\mathbb E}[S_{nt}])$
on
![]() $[0,1]$
. We also obtain a functional CLT.
$[0,1]$
. We also obtain a functional CLT.
Theorem 2.19. Let
![]() ${\mathcal L}$
be a good cocycle. Suppose that
${\mathcal L}$
be a good cocycle. Suppose that
![]() $\operatorname {\mathrm {esssup}}_{{\omega }\in {\Omega }}(K({\omega })\|\varphi _{\omega }\|_{BV})<\infty $
and that Assumption 2.13 holds true. Then the random function
$\operatorname {\mathrm {esssup}}_{{\omega }\in {\Omega }}(K({\omega })\|\varphi _{\omega }\|_{BV})<\infty $
and that Assumption 2.13 holds true. Then the random function
![]() ${\mathcal S}_n$
converges in distribution towards the distribution of
${\mathcal S}_n$
converges in distribution towards the distribution of
![]() $\{sW_t\}$
, where W is a standard Brownian motion (restricted to
$\{sW_t\}$
, where W is a standard Brownian motion (restricted to
![]() $[0,1]$
) and
$[0,1]$
) and
![]() $s^2$
is the asymptotic variance.
$s^2$
is the asymptotic variance.
Remark 2.20. The proof of Theorem 2.19 appears in §3.3. In [Reference Aimino, Nicol and Vaienti2] an ASIP was obtained, which yields the functional CLT. In §2.5.2 below, using different mixing coefficients for the base map, we will obtain an ASIP for the more general skew products considered in this paper. However, Theorem 2.19 shows that the functional CLT already holds true for stretched exponential
![]() ${\alpha }$
-mixing base maps.
${\alpha }$
-mixing base maps.
2.5.2 An almost sure invariance principle and exponential concentration inequalities for
 $\phi $
- and
$\phi $
- and
 $\psi $
-mixing driving processes (via martingale methods)
$\psi $
-mixing driving processes (via martingale methods)
Let
![]() $({\Omega }_0,\mathscr F,\textbf {P})$
be the probability space on which
$({\Omega }_0,\mathscr F,\textbf {P})$
be the probability space on which
![]() $(\xi _n)$
is defined. We recall that the
$(\xi _n)$
is defined. We recall that the
![]() $\phi $
-mixing and
$\phi $
-mixing and
![]() $\psi $
(dependence) coefficient between two sub-
$\psi $
(dependence) coefficient between two sub-
![]() ${\sigma }$
-algebras
${\sigma }$
-algebras
![]() ${\mathcal G},{\mathcal H}$
of
${\mathcal G},{\mathcal H}$
of
![]() $\mathscr F$
is given by
$\mathscr F$
is given by
and
 $$ \begin{align*} \psi({\mathcal G},{\mathcal H})=\sup\bigg\{\bigg|\frac{\textbf{P}(A\cap B)}{\textbf{P}(A)\textbf{P}(B)}-1\bigg|: A\in{\mathcal G}, B\in{\mathcal H}, \textbf{P}(A)\textbf{P}(B)>0\bigg\}. \end{align*} $$
$$ \begin{align*} \psi({\mathcal G},{\mathcal H})=\sup\bigg\{\bigg|\frac{\textbf{P}(A\cap B)}{\textbf{P}(A)\textbf{P}(B)}-1\bigg|: A\in{\mathcal G}, B\in{\mathcal H}, \textbf{P}(A)\textbf{P}(B)>0\bigg\}. \end{align*} $$
The reverse
![]() $\phi $
-mixing coefficients of
$\phi $
-mixing coefficients of
![]() $(\xi _n)$
are defined by
$(\xi _n)$
are defined by
while the
![]() $\psi $
-mixing coefficients of
$\psi $
-mixing coefficients of
![]() $(\xi _n)$
are defined by
$(\xi _n)$
are defined by
where
![]() $\mathscr F_{-\infty ,k}$
is the
$\mathscr F_{-\infty ,k}$
is the
![]() $\sigma $
-algebra generated by
$\sigma $
-algebra generated by
![]() $\xi _j$
,
$\xi _j$
,
![]() $j\leq k$
, and
$j\leq k$
, and
![]() $\mathscr F_{k+n,\infty }$
is generated by
$\mathscr F_{k+n,\infty }$
is generated by
![]() $\xi _j, j\geq k+n$
. It is clear from the definitions of the mixing coefficients that
$\xi _j, j\geq k+n$
. It is clear from the definitions of the mixing coefficients that
Theorem 2.21. (Exponential concentration and maximal inequalities)
Let
![]() ${\mathcal L}$
be a good cocycle. Suppose the observable satisfies
${\mathcal L}$
be a good cocycle. Suppose the observable satisfies
![]() $\operatorname {\mathrm {esssup}}_{{\omega }\in {\Omega }}(K({\omega })^2\|\varphi _{\omega }\|_{BV})<\infty $
.
$\operatorname {\mathrm {esssup}}_{{\omega }\in {\Omega }}(K({\omega })^2\|\varphi _{\omega }\|_{BV})<\infty $
.
Let
![]() ${\mathcal F}_0$
be the
${\mathcal F}_0$
be the
![]() $\sigma $
algebra generated by the map
$\sigma $
algebra generated by the map
![]() $\pi ({\omega },x)=(({\omega }_j)_{j\geq 0},x)$
, namely the one generated by
$\pi ({\omega },x)=(({\omega }_j)_{j\geq 0},x)$
, namely the one generated by
![]() ${\mathcal B}$
and the coordinates with non-negative indexes in the
${\mathcal B}$
and the coordinates with non-negative indexes in the
![]() ${\omega }$
direction. If either
${\omega }$
direction. If either
![]() $\mathrm {essinf}\inf _{x} h_{\omega }(x)>0$
and
$\mathrm {essinf}\inf _{x} h_{\omega }(x)>0$
and
![]() $\sum _{n}\phi _{n,R}<\infty $
or
$\sum _{n}\phi _{n,R}<\infty $
or
![]() $\sum _{n}\psi _{n}<\infty $
then there is an
$\sum _{n}\psi _{n}<\infty $
then there is an
![]() ${\mathcal F}_0$
-measurable function
${\mathcal F}_0$
-measurable function
![]() $\chi \in L^\infty (\mu )$
such that if we set
$\chi \in L^\infty (\mu )$
such that if we set
![]() $u=\varphi +\chi \circ \tau -\chi $
then
$u=\varphi +\chi \circ \tau -\chi $
then
![]() $(u\circ \tau ^n)$
is a reverse martingale difference with respect to the reverse filtration
$(u\circ \tau ^n)$
is a reverse martingale difference with respect to the reverse filtration
![]() $\{\tau ^{-n}{\mathcal F}_0\}$
. As a consequence, we have the following assertions.
$\{\tau ^{-n}{\mathcal F}_0\}$
. As a consequence, we have the following assertions.
-
(i) There are constants
 $a_1,a_2,a_3>0$
such that the following exponential concentration inequality holds true: for every
$a_1,a_2,a_3>0$
such that the following exponential concentration inequality holds true: for every
 $t>0$
, we have (2.25)The constants
$t>0$
, we have (2.25)The constants $$ \begin{align} \mu(|S_n-{\mathbb E}_\mu[S_n]|\geq tn+a_1)\leq a_2e^{-a_3 nt^2}. \end{align} $$
$$ \begin{align} \mu(|S_n-{\mathbb E}_\mu[S_n]|\geq tn+a_1)\leq a_2e^{-a_3 nt^2}. \end{align} $$
 $a_1,a_2,a_3$
depend only on
$a_1,a_2,a_3$
depend only on
 $\tilde \Phi =\sum _{n}\phi _{n,R}<\infty $
and c (or
$\tilde \Phi =\sum _{n}\phi _{n,R}<\infty $
and c (or
 $\tilde \Psi =\sum _{n}\psi _{n}<\infty $
), the constant
$\tilde \Psi =\sum _{n}\psi _{n}<\infty $
), the constant
 $C_{\mathrm {v}}$
and
$C_{\mathrm {v}}$
and
 $\|\varphi \|_{K,2}=\operatorname {\mathrm {esssup}}_{{\omega }\in {\Omega }}(K({\omega })^2\|\varphi _{\omega }\|_{BV})$
, and an explicit formula for them can be recovered from the proof.
$\|\varphi \|_{K,2}=\operatorname {\mathrm {esssup}}_{{\omega }\in {\Omega }}(K({\omega })^2\|\varphi _{\omega }\|_{BV})$
, and an explicit formula for them can be recovered from the proof.
-
(ii) For every
 $p\geq 2$
, we have (2.26)where
$p\geq 2$
, we have (2.26)where $$ \begin{align} \Big\|\!\max_{1\leq k\leq n}|S_k-{\mathbb E}[S_k]|\Big\|_{L^p(\mu)}\leq C_pn^{1/2}, \end{align} $$
$$ \begin{align} \Big\|\!\max_{1\leq k\leq n}|S_k-{\mathbb E}[S_k]|\Big\|_{L^p(\mu)}\leq C_pn^{1/2}, \end{align} $$
 $C_p>0$
is a constant (which can be recovered from the proof and depends only on p and the above constants).
$C_p>0$
is a constant (which can be recovered from the proof and depends only on p and the above constants).
We refer readers to [Reference Korepanov and Leppanen43] for some related moment bounds for random intermittent maps.
The proof of Theorem 2.21 appears in §4. Let us note that once the martingale-coboundary representation
![]() $\varphi =u+\chi -\chi \circ \tau $
is established, Theorem 2.21(i) follows from the Azuma–Hoeffding inequality together with Chernoff’s bounding method, and Theorem 2.21(ii) follows from the so-called Rio inequality [Reference Rio48] (see [Reference Merlevéde, Peligrad and Utev45, Proposition 7]).
$\varphi =u+\chi -\chi \circ \tau $
is established, Theorem 2.21(i) follows from the Azuma–Hoeffding inequality together with Chernoff’s bounding method, and Theorem 2.21(ii) follows from the so-called Rio inequality [Reference Rio48] (see [Reference Merlevéde, Peligrad and Utev45, Proposition 7]).
To obtain the martingale-coboundary representation we show that if
![]() ${\mathcal K}$
is the transfer operator (namely, the one satisfying the duality relation
${\mathcal K}$
is the transfer operator (namely, the one satisfying the duality relation
corresponding to the system
![]() $({\Omega }\times X,{\mathcal F}_0,\mu ,\tau )$
then there is a constant
$({\Omega }\times X,{\mathcal F}_0,\mu ,\tau )$
then there is a constant
![]() $C>0$
such that
$C>0$
such that
where
![]() $\gamma _n$
is either
$\gamma _n$
is either
![]() $\psi _{n}$
or
$\psi _{n}$
or
![]() $\phi _{n,R}$
, depending on the case, and
$\phi _{n,R}$
, depending on the case, and
![]() ${\delta }\in (0,1)$
. Once this is established we can take
${\delta }\in (0,1)$
. Once this is established we can take
The proof of (2.27) is given in Proposition 4.3 (i).
Our next result is an ASIP.
Theorem 2.22. (ASIP)
Let
![]() ${\mathcal L}$
be a good cocycle, and suppose that the observable satisfies
${\mathcal L}$
be a good cocycle, and suppose that the observable satisfies
![]() $\operatorname {\mathrm {esssup}}_{{\omega }\in {\Omega }}(K({\omega })^2\|\varphi _{\omega }\|_{BV})<\infty $
.
$\operatorname {\mathrm {esssup}}_{{\omega }\in {\Omega }}(K({\omega })^2\|\varphi _{\omega }\|_{BV})<\infty $
.
When
![]() $\mathrm {essinf}\,\inf _{x} h_{\omega }(x)>0$
we set
$\mathrm {essinf}\,\inf _{x} h_{\omega }(x)>0$
we set
![]() $\gamma _n=\phi _{R,n}$
, while otherwise we set
$\gamma _n=\phi _{R,n}$
, while otherwise we set
![]() $\gamma _n=\psi _n$
. In both cases, assume that
$\gamma _n=\psi _n$
. In both cases, assume that
and
 $$ \begin{align*} \sum_{n\geq 2}\frac{(\log n)^3}{n^2}\bigg(\sum_{k=0}^n(k+1)\gamma_k\bigg)^2<\infty. \end{align*} $$
$$ \begin{align*} \sum_{n\geq 2}\frac{(\log n)^3}{n^2}\bigg(\sum_{k=0}^n(k+1)\gamma_k\bigg)^2<\infty. \end{align*} $$
Then the limit
exists and the following version of the ASIP holds true: there is a coupling of
![]() $(\varphi \circ \tau ^n)$
with a sequence of i.i.d. Gaussian random variables
$(\varphi \circ \tau ^n)$
with a sequence of i.i.d. Gaussian random variables
![]() $Z_j$
with zero mean and variance
$Z_j$
with zero mean and variance
![]() $s^2$
such that
$s^2$
such that
 $$ \begin{align*} \sup_{1\leq k\leq n}\bigg|(S_k-{\mathbb E}[S_k])-\sum_{j=1}^k Z_j\bigg|=O(n^{1/4}(\log n)^{1/2}(\log\log n)^{1/4})\quad\text{almost surely}. \end{align*} $$
$$ \begin{align*} \sup_{1\leq k\leq n}\bigg|(S_k-{\mathbb E}[S_k])-\sum_{j=1}^k Z_j\bigg|=O(n^{1/4}(\log n)^{1/2}(\log\log n)^{1/4})\quad\text{almost surely}. \end{align*} $$
Remark 2.23. The ASIP implies the functional CLT, see [Reference Philipp and Stout47]. Thus, Theorem 2.22 yields better results than Theorem 2.19 for
![]() $\phi _R$
- or
$\phi _R$
- or
![]() $\psi $
-mixing driving sequences (which are not necessarily stretched exponentially mixing).
$\psi $
-mixing driving sequences (which are not necessarily stretched exponentially mixing).
The proof of Theorem 2.22 appears in §4 and relies on an application of [Reference Cuny and Merlevede13, Theorem 3.2]. In addition to (2.27), in order to apply [Reference Cuny and Merlevede13, Theorem 3.2] we will show that for all
![]() $1\leq i,j\leq n$
we have
$1\leq i,j\leq n$
we have
where
![]() $\bar \varphi =\varphi -\mu (\varphi )$
, C is a constant and
$\bar \varphi =\varphi -\mu (\varphi )$
, C is a constant and
![]() ${\delta }$
and
${\delta }$
and
![]() $\gamma _n$
are as in (2.27). The proof of (2.28) is given in Proposition 4.3 (ii).
$\gamma _n$
are as in (2.27). The proof of (2.28) is given in Proposition 4.3 (ii).
Remark 2.24. As discussed in §1.3.2, the martingale-coboundary decomposition in Theorem 2.21 (and its consequences) is comparable with the annealed case [Reference Aimino, Nicol and Vaienti2], and the main novelty is that we obtain it for more general skew products and functions
![]() $\varphi $
which depend on
$\varphi $
which depend on
![]() ${\omega }$
. Moreover, we do not assume that all
${\omega }$
. Moreover, we do not assume that all
![]() $T_{\omega }$
preserve the same absolutely continuous probability measure. The ASIPs we obtain are comparable to ASIPs in [Reference Aimino, Nicol and Vaienti2] (see the discussion in §1.3.2).
$T_{\omega }$
preserve the same absolutely continuous probability measure. The ASIPs we obtain are comparable to ASIPs in [Reference Aimino, Nicol and Vaienti2] (see the discussion in §1.3.2).
2.5.3 A vector-valued almost sure invariance principle in the uniformly random case for exponentially fast
 $\alpha $
-mixing base maps
$\alpha $
-mixing base maps
Let us take a vector-valued measurable function
![]() $\varphi =(\varphi _1\ldots \varphi _d):{\Omega }\times X\to {\mathbb R}^d$
such that
$\varphi =(\varphi _1\ldots \varphi _d):{\Omega }\times X\to {\mathbb R}^d$
such that
![]() $\varphi _{\omega }=\varphi ({\omega },\cdot )$
depend on
$\varphi _{\omega }=\varphi ({\omega },\cdot )$
depend on
![]() ${\omega }$
only through
${\omega }$
only through
![]() ${\omega }_0$
and
${\omega }_0$
and
![]() $\operatorname {\mathrm {esssup}}_{{\omega }\in {\Omega }}(K({\omega })\|\varphi _{{\omega },i}\|_{BV})<\infty $
for all
$\operatorname {\mathrm {esssup}}_{{\omega }\in {\Omega }}(K({\omega })\|\varphi _{{\omega },i}\|_{BV})<\infty $
for all
![]() $1\leq i\leq d$
. Let us also assume that
$1\leq i\leq d$
. Let us also assume that
![]() $\mu (\varphi _i)=0$
for every i. Set
$\mu (\varphi _i)=0$
for every i. Set
![]() $S_n=\sum _{j=0}^{n-1}\varphi \circ \tau ^j$
.
$S_n=\sum _{j=0}^{n-1}\varphi \circ \tau ^j$
.
Theorem 2.25. Suppose that
![]() ${\alpha }_n=O({\alpha }^n)$
for some
${\alpha }_n=O({\alpha }^n)$
for some
![]() ${\alpha }\in (0,1)$
. Then there is a positive semidefinite matrix
${\alpha }\in (0,1)$
. Then there is a positive semidefinite matrix
![]() ${\Sigma }^2$
such that
${\Sigma }^2$
such that
Moreover,
![]() ${\Sigma }^2$
is positive definite if and only if
${\Sigma }^2$
is positive definite if and only if
![]() $\varphi \cdot v \neq r-r\circ \tau $
for all unit vectors v and all
$\varphi \cdot v \neq r-r\circ \tau $
for all unit vectors v and all
![]() $r\in L^2$
.
$r\in L^2$
.
Assume now that there are constants
![]() $C>0$
and
$C>0$
and
![]() ${\delta }\in (0,1)$
so that
${\delta }\in (0,1)$
so that
namely, that
![]() $K({\omega })$
is a bounded random variable. Then there is a coupling of
$K({\omega })$
is a bounded random variable. Then there is a coupling of
![]() ${(\varphi \circ \tau ^n)}$
with a sequence of independent Gaussian centered random vectors
${(\varphi \circ \tau ^n)}$
with a sequence of independent Gaussian centered random vectors
![]() $(Z_n)$
such that
$(Z_n)$
such that
![]() ${\mathrm {Cov}(Z_n)={\Sigma }^2}$
and for every
${\mathrm {Cov}(Z_n)={\Sigma }^2}$
and for every
![]() ${\varepsilon }>0$
,
${\varepsilon }>0$
,
 $$ \begin{align*} \bigg|(S_n-{\mathbb E}[S_n])-\sum_{j=1}^n Z_j\bigg|=o(n^{1/4+{\varepsilon}})\quad\text{almost surely}. \end{align*} $$
$$ \begin{align*} \bigg|(S_n-{\mathbb E}[S_n])-\sum_{j=1}^n Z_j\bigg|=o(n^{1/4+{\varepsilon}})\quad\text{almost surely}. \end{align*} $$
3 Limit theorems via the method of cumulants for
 ${\alpha }$
-mixing driving processes
${\alpha }$
-mixing driving processes
We recall next that the kth cumulant of a random variable W with finite moments of all orders is given by
Note that
![]() ${\Gamma }_1(W)={\mathbb E}[W]$
,
${\Gamma }_1(W)={\mathbb E}[W]$
,
![]() ${\Gamma }_2(W)=\mathrm {Var}(W)$
, and
${\Gamma }_2(W)=\mathrm {Var}(W)$
, and
![]() ${\Gamma }_k(aW)=a^k{\Gamma }_k(W)$
for any
${\Gamma }_k(aW)=a^k{\Gamma }_k(W)$
for any
![]() $a\in {\mathbb R}$
and
$a\in {\mathbb R}$
and
![]() $k\geq 1$
.
$k\geq 1$
.
From now on we will assume that
![]() ${\mathbb E}[S_n]=0$
for all n, that is, we will replace
${\mathbb E}[S_n]=0$
for all n, that is, we will replace
![]() $\varphi $
by
$\varphi $
by
![]() $\varphi -\mu (\varphi )$
. The main result in this section is the following theorem.
$\varphi -\mu (\varphi )$
. The main result in this section is the following theorem.
Theorem 3.1. Let
![]() ${\mathcal L}$
be a good cocycle, and suppose that Assumption 2.13 holds true and that
${\mathcal L}$
be a good cocycle, and suppose that Assumption 2.13 holds true and that
![]() $\|\varphi \|_{K}=\operatorname {\mathrm {esssup}}_{{\omega }\in {\Omega }}(K({\omega })\|\varphi _{\omega }\|_{BV})<\infty $
. Then, with
$\|\varphi \|_{K}=\operatorname {\mathrm {esssup}}_{{\omega }\in {\Omega }}(K({\omega })\|\varphi _{\omega }\|_{BV})<\infty $
. Then, with
![]() $\gamma =1/\eta $
, there exists a constant
$\gamma =1/\eta $
, there exists a constant
![]() $c_0$
which depends only on
$c_0$
which depends only on
![]() $\|\varphi \|_K$
and the constants from Assumption 2.13 such that, for any
$\|\varphi \|_K$
and the constants from Assumption 2.13 such that, for any
![]() $k\geq 3$
,
$k\geq 3$
,
We will prove Theorem 3.1 by applying the following Proposition 3.3, which appears in [Reference Hafouta25] as Corollary 3.2.
Let us start with a few preparations. Let V be a finite set and
![]() $\rho :V\times V\to [0,\infty )$
be such that
$\rho :V\times V\to [0,\infty )$
be such that
![]() $\rho (v,v)=0$
and
$\rho (v,v)=0$
and
![]() $\rho (u,v)=\rho (v,u)$
for all
$\rho (u,v)=\rho (v,u)$
for all
![]() $u,v\in V$
. For every
$u,v\in V$
. For every
![]() $A,B\subset V$
set
$A,B\subset V$
set
We assume here that there exist
![]() $c_0\geq 1$
and
$c_0\geq 1$
and
![]() $u_0\geq 0$
such that
$u_0\geq 0$
such that
for all
![]() $v\in V$
and
$v\in V$
and
![]() $s\geq 1$
.
$s\geq 1$
.
Next, let
![]() $X_v,\, v\in V$
be a collection of centered random variables with finite moments of all orders, and for each
$X_v,\, v\in V$
be a collection of centered random variables with finite moments of all orders, and for each
![]() $v\in V$
and
$v\in V$
and
![]() $t\in (0,\infty ]$
let
$t\in (0,\infty ]$
let
![]() $\varrho _{v,t}\in (0,\infty ]$
be such that
$\varrho _{v,t}\in (0,\infty ]$
be such that
![]() $\|X_v\|_t\leq \varrho _{v,t}$
.
$\|X_v\|_t\leq \varrho _{v,t}$
.
Assumption 3.2. For some
![]() $0<{\delta }\leq \infty $
and all
$0<{\delta }\leq \infty $
and all
![]() $k\geq 1$
,
$k\geq 1$
,
![]() $b>0$
and a finite collection
$b>0$
and a finite collection
![]() $A_j$
,
$A_j$
,
![]() $j\in {\mathcal J}$
, of (non-empty) subsets of V such that
$j\in {\mathcal J}$
, of (non-empty) subsets of V such that
![]() $\min _{i\not =j}\rho (A_i,A_j)\geq b$
and
$\min _{i\not =j}\rho (A_i,A_j)\geq b$
and
![]() $r:=\sum _{j\in {\mathcal J}} |A_j|\leq k$
, we have
$r:=\sum _{j\in {\mathcal J}} |A_j|\leq k$
, we have
 $$ \begin{align} \bigg|{\mathbb E}\bigg[\prod_{j\in{\mathcal J}}\prod_{i\in A_j}X_i\bigg]-\prod_{i\in{\mathcal J}} {\mathbb E}\bigg[\prod_{j\in A_j}X_i\bigg]\bigg|\leq (r-1)\bigg(\prod_{i\in{\mathcal J}}\prod_{i\in A_j}\varrho_{i,(1+{\delta})k}\bigg){\gamma}_{\delta}(b,k), \end{align} $$
$$ \begin{align} \bigg|{\mathbb E}\bigg[\prod_{j\in{\mathcal J}}\prod_{i\in A_j}X_i\bigg]-\prod_{i\in{\mathcal J}} {\mathbb E}\bigg[\prod_{j\in A_j}X_i\bigg]\bigg|\leq (r-1)\bigg(\prod_{i\in{\mathcal J}}\prod_{i\in A_j}\varrho_{i,(1+{\delta})k}\bigg){\gamma}_{\delta}(b,k), \end{align} $$
where
![]() ${\gamma }_{\delta }(b,r)$
is some non-negative number which depends only on
${\gamma }_{\delta }(b,r)$
is some non-negative number which depends only on
![]() ${\delta },b$
and r, and
${\delta },b$
and r, and
![]() $|{\Delta }|$
stands for the cardinality of a finite set
$|{\Delta }|$
stands for the cardinality of a finite set
![]() ${\Delta }$
.
${\Delta }$
.
Set
![]() $W=\sum _{v\in V} X_v$
. In the course of the proof of Theorems 2.14–2.16 and 2.19 we will need the following general result.
$W=\sum _{v\in V} X_v$
. In the course of the proof of Theorems 2.14–2.16 and 2.19 we will need the following general result.
Proposition 3.3. [Reference Hafouta25, Corollary 3.2]
Suppose that inequality (3.1) and Assumption 3.2 are in force. Assume also that
for some
![]() $a,\eta>0$
,
$a,\eta>0$
,
![]() $d\geq 1$
and all
$d\geq 1$
and all
![]() $k,m\geq 1$
. Then there exists a constant c which depends only on
$k,m\geq 1$
. Then there exists a constant c which depends only on
![]() $c_0,a,u_0$
and
$c_0,a,u_0$
and
![]() $\eta $
such that, for every
$\eta $
such that, for every
![]() $k\geq 2$
,
$k\geq 2$
,
where for all
![]() $q>0$
,
$q>0$
,
When the
![]() $X_v$
are bounded and (3.2) holds true with
$X_v$
are bounded and (3.2) holds true with
![]() ${\delta }=\infty $
we can always take
${\delta }=\infty $
we can always take
![]() ${\varrho _{v,t}=\varrho _{v,\infty }}$
,
${\varrho _{v,t}=\varrho _{v,\infty }}$
,
![]() $t>0$
, and then, for any
$t>0$
, and then, for any
![]() $k\geq 2$
,
$k\geq 2$
,
When
![]() ${\delta }<\infty $
and there exist
${\delta }<\infty $
and there exist
![]() ${\theta }\geq 0$
and
${\theta }\geq 0$
and
![]() $M>0$
such that
$M>0$
such that
for any
![]() $v\in V$
and
$v\in V$
and
![]() $k\geq 1$
, we have that, for any
$k\geq 1$
, we have that, for any
![]() $k\geq 2$
,
$k\geq 2$
,
where C is some absolute constant.
Theorem 3.1 will follow from the following result, which is proved in §3.1.
Proposition 3.4. For a good cocycle
![]() ${\mathcal L}$
and an observable
${\mathcal L}$
and an observable
![]() $\varphi $
satisfying (2.16) we have the following assertion. Fix some n and set
$\varphi $
satisfying (2.16) we have the following assertion. Fix some n and set
![]() $V=\{0,1,\ldots , n-1\}$
and
$V=\{0,1,\ldots , n-1\}$
and
![]() $X_v=\varphi \circ \tau ^v$
. Set also
$X_v=\varphi \circ \tau ^v$
. Set also
![]() $\rho (x,y)=|x-y|$
, and let
$\rho (x,y)=|x-y|$
, and let
![]() $t=\delta =\infty $
,
$t=\delta =\infty $
,
![]() $\gamma _{\infty }(b,k)=\gamma _b=e^{-({\unicode{x3bb} }-{\varepsilon })b/3}+{\alpha }_{[b/3]}$
. Then condition (3.2) holds true with the above choices and with
$\gamma _{\infty }(b,k)=\gamma _b=e^{-({\unicode{x3bb} }-{\varepsilon })b/3}+{\alpha }_{[b/3]}$
. Then condition (3.2) holds true with the above choices and with
where
![]() $A_0$
is a constant which depends only on
$A_0$
is a constant which depends only on
![]() ${\unicode{x3bb} }-3{\varepsilon }$
and on the constant C so that
${\unicode{x3bb} }-3{\varepsilon }$
and on the constant C so that
![]() $\sup |g|\leq C\|g\|_{BV}$
for every function
$\sup |g|\leq C\|g\|_{BV}$
for every function
![]() $g:X\to {\mathbb C}$
(and the dependence can be easily recovered from the proof).
$g:X\to {\mathbb C}$
(and the dependence can be easily recovered from the proof).
If, in addition, Assumption 2.13 holds then the conditions of Proposition 3.3 hold true with
![]() $u_0=1$
,
$u_0=1$
,
![]() $c_0=2$
and
$c_0=2$
and
![]() $\gamma =1/\eta $
.
$\gamma =1/\eta $
.
3.1 Multiple correlation estimates: proof of Proposition 3.4
Our goal is to show that (3.2) holds true with the desired upper bounds. We first need the following result.
Lemma 3.5. For every pair of measurable functions
![]() $g,h$
on
$g,h$
on
![]() $\mathcal Y^{\mathbb N}$
with
$\mathcal Y^{\mathbb N}$
with
![]() $g,h\in L^\infty $
(with respect to the law of
$g,h\in L^\infty $
(with respect to the law of
![]() $(\xi _n)$
) and all
$(\xi _n)$
) and all
![]() $k\in \mathbb Z$
and
$k\in \mathbb Z$
and
![]() $n\in \mathbb N$
, we have
$n\in \mathbb N$
, we have
 $$ \begin{align} &|\mathbb E[g(\ldots,\xi_{k-1},\xi_k)h(\xi_{k+n},\xi_{k+n+1},\ldots)]\nonumber\\&\qquad-\mathbb E[g(\ldots,\xi_{k-1},\xi_k)]\cdot\mathbb E[h(\xi_{k+n},\xi_{k+n+1},\ldots)]|\\&\quad\leq \tfrac14 \|g(\ldots,\xi_{k-1},\xi_k)\|_{L^\infty}\|h(\xi_{k+n},\xi_{k+n+1},\ldots)\|_{L^\infty} \alpha_n.\nonumber\end{align} $$
$$ \begin{align} &|\mathbb E[g(\ldots,\xi_{k-1},\xi_k)h(\xi_{k+n},\xi_{k+n+1},\ldots)]\nonumber\\&\qquad-\mathbb E[g(\ldots,\xi_{k-1},\xi_k)]\cdot\mathbb E[h(\xi_{k+n},\xi_{k+n+1},\ldots)]|\\&\quad\leq \tfrac14 \|g(\ldots,\xi_{k-1},\xi_k)\|_{L^\infty}\|h(\xi_{k+n},\xi_{k+n+1},\ldots)\|_{L^\infty} \alpha_n.\nonumber\end{align} $$
Proof. By [Reference Bradley11, Ch. 4], we have
Taking
![]() $g\kern1.5pt{=}\kern1.5pt g(\ldots ,\xi _{k-1},\xi _k)$
and
$g\kern1.5pt{=}\kern1.5pt g(\ldots ,\xi _{k-1},\xi _k)$
and
![]() $h\kern1.5pt{=}\kern1.5pt h(\xi _{k+n},\xi _{k+n+1},\ldots )$
,
$h\kern1.5pt{=}\kern1.5pt h(\xi _{k+n},\xi _{k+n+1},\ldots )$
,
![]() ${\mathcal G}\kern1.5pt{=}\kern1.5pt\mathscr F_{-\infty ,k}$
and
${\mathcal G}\kern1.5pt{=}\kern1.5pt\mathscr F_{-\infty ,k}$
and
![]() ${\mathcal H}\kern1.5pt{=}\kern1.5pt\mathscr F_{k+n,\infty }$
, we get
${\mathcal H}\kern1.5pt{=}\kern1.5pt\mathscr F_{k+n,\infty }$
, we get
Next, is it clearly enough to prove Proposition 3.4 when
![]() $\|\varphi \|_{L^\infty }$
and
$\|\varphi \|_{L^\infty }$
and
![]() $\operatorname {\mathrm {esssup}}_{{\omega }\in {\Omega }}(K({\omega }) \|\varphi _{\omega }\|_{BV})$
do not exceed
$\operatorname {\mathrm {esssup}}_{{\omega }\in {\Omega }}(K({\omega }) \|\varphi _{\omega }\|_{BV})$
do not exceed
![]() $1$
, for otherwise we can just divide
$1$
, for otherwise we can just divide
![]() $\varphi $
by the maximum between the two. Recall also our assumption that
$\varphi $
by the maximum between the two. Recall also our assumption that
![]() $K(\omega )e^{-{\varepsilon } |m|}\leq K(\sigma ^{m}\omega )\leq K(\omega )e^{{\varepsilon } |m|}$
for some
$K(\omega )e^{-{\varepsilon } |m|}\leq K(\sigma ^{m}\omega )\leq K(\omega )e^{{\varepsilon } |m|}$
for some
![]() ${\varepsilon }<\unicode{x3bb} /3$
(recall Remark 2.11).
${\varepsilon }<\unicode{x3bb} /3$
(recall Remark 2.11).
The first step in the proof of Proposition 3.4 is the following result.
Lemma 3.6. (Fiberwise multiple correlation estimates)
Let
![]() $B_1,B_2,\ldots , B_m$
be non-empty intervals in the non-negative integers so that
$B_1,B_2,\ldots , B_m$
be non-empty intervals in the non-negative integers so that
![]() $B_i$
is to the left of
$B_i$
is to the left of
![]() $B_{i+1}$
and
$B_{i+1}$
and
![]() $B_1$
contains
$B_1$
contains
![]() $0$
. Let us denote by
$0$
. Let us denote by
![]() $d_i$
the gap between
$d_i$
the gap between
![]() $B_i$
and
$B_i$
and
![]() $B_{i+1}$
(namely, the distance). Let us fix some
$B_{i+1}$
(namely, the distance). Let us fix some
![]() $\omega $
and let
$\omega $
and let
![]() $f_i$
be a family of functions such that
$f_i$
be a family of functions such that
![]() $K(\sigma ^i\omega )\|f_i\|_{BV}\leq 1$
and
$K(\sigma ^i\omega )\|f_i\|_{BV}\leq 1$
and
![]() $\|f_i\|_{L^\infty }\leq 1$
. Let us define
$\|f_i\|_{L^\infty }\leq 1$
. Let us define
![]() $F_j=F_{B_j,\omega }=\prod _{i\in B_j}f_i\circ T_\omega ^i$
. Then
$F_j=F_{B_j,\omega }=\prod _{i\in B_j}f_i\circ T_\omega ^i$
. Then
 $$ \begin{align*} \bigg|\bigg(\int \bigg(\prod_{j=1}^{m}F_j\bigg)\,d\mu_\omega\bigg)-\bigg(\prod_{j=1}^m\int F_jd\mu_\omega\bigg)\bigg|\leq A\sum_{j=1}^{m-1}e^{-(\unicode{x3bb}-{\varepsilon}) d_j}, \end{align*} $$
$$ \begin{align*} \bigg|\bigg(\int \bigg(\prod_{j=1}^{m}F_j\bigg)\,d\mu_\omega\bigg)-\bigg(\prod_{j=1}^m\int F_jd\mu_\omega\bigg)\bigg|\leq A\sum_{j=1}^{m-1}e^{-(\unicode{x3bb}-{\varepsilon}) d_j}, \end{align*} $$
where
![]() $A=C^2\sup _{d\in \mathbb N}2de^{-(\unicode{x3bb} -{\varepsilon })d}$
and
$A=C^2\sup _{d\in \mathbb N}2de^{-(\unicode{x3bb} -{\varepsilon })d}$
and
![]() ${\unicode{x3bb} }$
comes from (2.10) and (2.14) (recall Remark 2.11).
${\unicode{x3bb} }$
comes from (2.10) and (2.14) (recall Remark 2.11).
Proof. The proof will proceed by induction on m. Let us first prove the lemma in the case
![]() $m=2$
. We first note that for all functions
$m=2$
. We first note that for all functions
![]() $g_0,g_1,\ldots , g_q$
, we have
$g_0,g_1,\ldots , g_q$
, we have
 $$ \begin{align*} \mathrm{v}\bigg(\prod_{k=0}^{q}g_k\circ T_\omega^k\bigg)\leq\sum_{k=0}^q \bigg(\prod_{0\leq s<k}\|g_s\|_\infty\bigg)\cdot(\mathrm{v}(g_k\circ T_\omega^k))\cdot\bigg(\prod_{k<s\leq q}\|g_s\|_\infty\bigg) \end{align*} $$
$$ \begin{align*} \mathrm{v}\bigg(\prod_{k=0}^{q}g_k\circ T_\omega^k\bigg)\leq\sum_{k=0}^q \bigg(\prod_{0\leq s<k}\|g_s\|_\infty\bigg)\cdot(\mathrm{v}(g_k\circ T_\omega^k))\cdot\bigg(\prod_{k<s\leq q}\|g_s\|_\infty\bigg) \end{align*} $$
where
![]() $\|g_i\|_\infty =\sup \|g_i\|_{L^\infty }$
, and hence
$\|g_i\|_\infty =\sup \|g_i\|_{L^\infty }$
, and hence
 $$ \begin{align} \bigg\|\prod_{k=0}^qg_k\circ T_\omega^k\bigg\|_{BV}&\leq\prod_{k=0}^q\|g_k\|_\infty+\sum_{k=0}^q\bigg(\prod_{0\leq s<k}\|g_s\|_\infty\bigg)\nonumber\\ &\quad\times\bigg(\prod_{s=0}^{k-1}K(\sigma^s\omega)\mathrm{v}(g_k)\bigg)\bigg(\prod_{k<s\leq q}\|g_s\|_\infty\bigg), \end{align} $$
$$ \begin{align} \bigg\|\prod_{k=0}^qg_k\circ T_\omega^k\bigg\|_{BV}&\leq\prod_{k=0}^q\|g_k\|_\infty+\sum_{k=0}^q\bigg(\prod_{0\leq s<k}\|g_s\|_\infty\bigg)\nonumber\\ &\quad\times\bigg(\prod_{s=0}^{k-1}K(\sigma^s\omega)\mathrm{v}(g_k)\bigg)\bigg(\prod_{k<s\leq q}\|g_s\|_\infty\bigg), \end{align} $$
where we have used (2.3), that
![]() $N({\omega })\leq K({\omega })$
and that
$N({\omega })\leq K({\omega })$
and that
 $$ \begin{align*} \bigg\|\prod_{k=0}^qg_k\circ T_\omega^k\bigg\|_{L^1}\leq \bigg\|\prod_{k=0}^qg_k\circ T_\omega^k\bigg\|_{L^\infty}\leq \prod_{k=0}^q\|g_k\|_\infty. \end{align*} $$
$$ \begin{align*} \bigg\|\prod_{k=0}^qg_k\circ T_\omega^k\bigg\|_{L^1}\leq \bigg\|\prod_{k=0}^qg_k\circ T_\omega^k\bigg\|_{L^\infty}\leq \prod_{k=0}^q\|g_k\|_\infty. \end{align*} $$
Let us write
![]() $B_1=\{0,1,\ldots , d\}$
. Taking
$B_1=\{0,1,\ldots , d\}$
. Taking
![]() $g_k=f_k$
for
$g_k=f_k$
for
![]() $0\leq k\leq d=q$
and noting that
$0\leq k\leq d=q$
and noting that
![]() $K(\sigma ^s\omega )\|g_{s}\|_\infty \leq C$
for some constant C which depends (C is a constant which satisfies
$K(\sigma ^s\omega )\|g_{s}\|_\infty \leq C$
for some constant C which depends (C is a constant which satisfies
![]() $\|g\|_\infty =\sup |g|\leq C\|g\|_{BV}$
for every complex function on X) only the space X, we conclude that
$\|g\|_\infty =\sup |g|\leq C\|g\|_{BV}$
for every complex function on X) only the space X, we conclude that
Now, if we write
![]() $B_2=\{d+n,d+n+1,\ldots , d+n+L\}$
then
$B_2=\{d+n,d+n+1,\ldots , d+n+L\}$
then
where
By (2.14) we have
Therefore, using also that
![]() $\mu _\omega $
is an equivariant family and that (since
$\mu _\omega $
is an equivariant family and that (since
![]() $n+d\in B_2$
)
$n+d\in B_2$
)
we get that
 $$ \begin{align*} |\mu_\omega(F_1F_2)-\mu_\omega(F_1)\mu_{\omega}(F_2)|&=|\mu_{\sigma^{n+d}\omega}(G_2 L_\omega^{n+d}F_1)-\mu_\omega(F_1)\mu_{\sigma^{d+n} \omega}(G_2)|\\ &=\bigg|\int (L_\omega^{d+n}F_1-\mu_\omega(F_1))G_2 \, d\mu_{\sigma^{d+n} \omega}\bigg|\\ &\leq 2dCK(\omega)e^{-\unicode{x3bb}(d+n)}\|G_2\|_{L^\infty}\\ &\leq 2dCK(\omega)e^{-\unicode{x3bb}(d+n)}K(\sigma^{n+d}\omega)^{-1}\\ &\leq 2dC^2 e^{-(\unicode{x3bb}-{\varepsilon})(d+n)}\\ &=(2C^2de^{-(\unicode{x3bb}-{\varepsilon})d})e^{-(\unicode{x3bb}-{\varepsilon})n}. \end{align*} $$
$$ \begin{align*} |\mu_\omega(F_1F_2)-\mu_\omega(F_1)\mu_{\omega}(F_2)|&=|\mu_{\sigma^{n+d}\omega}(G_2 L_\omega^{n+d}F_1)-\mu_\omega(F_1)\mu_{\sigma^{d+n} \omega}(G_2)|\\ &=\bigg|\int (L_\omega^{d+n}F_1-\mu_\omega(F_1))G_2 \, d\mu_{\sigma^{d+n} \omega}\bigg|\\ &\leq 2dCK(\omega)e^{-\unicode{x3bb}(d+n)}\|G_2\|_{L^\infty}\\ &\leq 2dCK(\omega)e^{-\unicode{x3bb}(d+n)}K(\sigma^{n+d}\omega)^{-1}\\ &\leq 2dC^2 e^{-(\unicode{x3bb}-{\varepsilon})(d+n)}\\ &=(2C^2de^{-(\unicode{x3bb}-{\varepsilon})d})e^{-(\unicode{x3bb}-{\varepsilon})n}. \end{align*} $$
This proves the lemma for
![]() $m=2$
.
$m=2$
.
Next, let us complete the induction step. Let d be the right end point of
![]() $B_{m-1}$
. Then
$B_{m-1}$
. Then
![]() $d+d_m$
is the left end point of
$d+d_m$
is the left end point of
![]() $B_m$
and we can write
$B_m$
and we can write
 $$ \begin{align*} \mu_\omega\bigg(\prod_{k}F_k\bigg)=\mu_\omega \bigg(\prod_{k<m}F_k\cdot (G_m\circ T_{\omega}^{d+d_m})\bigg)= \mu_{\sigma^{d+d_m}{\omega}}\bigg(L_\omega^{d+d_m}\bigg(\prod_{k<m}F_k\bigg)\cdot G_m\bigg), \end{align*} $$
$$ \begin{align*} \mu_\omega\bigg(\prod_{k}F_k\bigg)=\mu_\omega \bigg(\prod_{k<m}F_k\cdot (G_m\circ T_{\omega}^{d+d_m})\bigg)= \mu_{\sigma^{d+d_m}{\omega}}\bigg(L_\omega^{d+d_m}\bigg(\prod_{k<m}F_k\bigg)\cdot G_m\bigg), \end{align*} $$
where
![]() $G_m$
is some function. Now we observe that
$G_m$
is some function. Now we observe that
 $$ \begin{align*} \bigg\|\prod_{k<m}F_k\bigg\|_{BV}\leq C(d+1)\leq 2Cd, \end{align*} $$
$$ \begin{align*} \bigg\|\prod_{k<m}F_k\bigg\|_{BV}\leq C(d+1)\leq 2Cd, \end{align*} $$
which is proved exactly as in the previous case (even though there are gaps between the blocks
![]() $B_j$
, we can set
$B_j$
, we can set
![]() $g_i=1$
when i does not belong to one of the
$g_i=1$
when i does not belong to one of the
![]() $B_j$
, and then
$B_j$
, and then
![]() $\mathrm {v}(g_i)=0$
). Thus, as in the case
$\mathrm {v}(g_i)=0$
). Thus, as in the case
![]() $m=2$
, we have
$m=2$
, we have
 $$ \begin{align*} \bigg|\mu_\omega\bigg(\prod_{k}F_k\bigg)-\mu_\omega(F_m)\mu_\omega\bigg(\prod_{k<m}F_k\bigg)\bigg|\leq (2C^2de^{-(\unicode{x3bb}-{\varepsilon})d})e^{-(\unicode{x3bb}-{\varepsilon})d_m}. \end{align*} $$
$$ \begin{align*} \bigg|\mu_\omega\bigg(\prod_{k}F_k\bigg)-\mu_\omega(F_m)\mu_\omega\bigg(\prod_{k<m}F_k\bigg)\bigg|\leq (2C^2de^{-(\unicode{x3bb}-{\varepsilon})d})e^{-(\unicode{x3bb}-{\varepsilon})d_m}. \end{align*} $$
The induction is completed by the above inequality, taking into account that
![]() ${|\mu _\omega (F_m)| \leq 1}$
.
${|\mu _\omega (F_m)| \leq 1}$
.
Integrating over
![]() ${\omega }$
yields the following corollary of Lemma 3.6.
${\omega }$
yields the following corollary of Lemma 3.6.
Corollary 3.7. Let
![]() $\tau $
be the skew product. Let
$\tau $
be the skew product. Let
![]() $B_j$
,
$B_j$
,
![]() $1\leq j\leq m$
, be blocks as in Lemma 3.6. Set
$1\leq j\leq m$
, be blocks as in Lemma 3.6. Set
![]() $G_j=\prod _{i\in B_j}\varphi \circ \tau ^{i}$
. Let us denote by
$G_j=\prod _{i\in B_j}\varphi \circ \tau ^{i}$
. Let us denote by
![]() $b_j$
the left end point of
$b_j$
the left end point of
![]() $B_j$
. Then
$B_j$
. Then
 $$ \begin{align} \bigg|\int \prod_{j=1}^{m} G_j \,d\mu-\int\bigg(\prod_{j=1}^{m}\int\bigg(\prod_{i\in B_j}\varphi_{\sigma^i\omega}\circ T_{{\sigma}^{b_j}{\omega}}^{i-b_j} \bigg)\,d\mu_{\sigma^{b_j}\omega}\bigg)\,d\mathbb P(\omega)\bigg|\leq A\sum_{j=1}^{d}e^{-\unicode{x3bb} d_j}. \end{align} $$
$$ \begin{align} \bigg|\int \prod_{j=1}^{m} G_j \,d\mu-\int\bigg(\prod_{j=1}^{m}\int\bigg(\prod_{i\in B_j}\varphi_{\sigma^i\omega}\circ T_{{\sigma}^{b_j}{\omega}}^{i-b_j} \bigg)\,d\mu_{\sigma^{b_j}\omega}\bigg)\,d\mathbb P(\omega)\bigg|\leq A\sum_{j=1}^{d}e^{-\unicode{x3bb} d_j}. \end{align} $$
The next step of the proof is to estimate the second term inside the absolute value on the left-hand side of (3.9). To obtain appropriate estimates, we first need the following lemma.
Lemma 3.8. Let us fix some
![]() $k\in \mathbb N$
and set
$k\in \mathbb N$
and set
 $$ \begin{align*} F_\omega=\prod_{j=0}^k\varphi_{\sigma^k\omega}\circ T_{\omega}^k. \end{align*} $$
$$ \begin{align*} F_\omega=\prod_{j=0}^k\varphi_{\sigma^k\omega}\circ T_{\omega}^k. \end{align*} $$
Then, for every
![]() $n\in \mathbb N$
and for
$n\in \mathbb N$
and for
![]() $\mathbb P$
-a.e.
$\mathbb P$
-a.e.
![]() $\omega $
, we have
$\omega $
, we have
where C is such that
![]() $\|g\|_{L^\infty }\leq C\|g\|_{BV}$
for every function g on X with bounded variation (recall that such a constant C exists by our assumption on the variation
$\|g\|_{L^\infty }\leq C\|g\|_{BV}$
for every function g on X with bounded variation (recall that such a constant C exists by our assumption on the variation
![]() $\mathrm {v}(\cdot )$
).
$\mathrm {v}(\cdot )$
).
Proof. Using (2.10), that
![]() $K({\sigma }^{-n}{\omega })\leq e^{{\varepsilon } n}K({\omega })$
and that
$K({\sigma }^{-n}{\omega })\leq e^{{\varepsilon } n}K({\omega })$
and that
![]() $\|F_\omega \|_{L^\infty }\leq \|\varphi _\omega \|_{L^\infty }\leq C\|\varphi _{\omega }\|_{BV}\leq CK({\omega })^{-1}$
, we obtain that
$\|F_\omega \|_{L^\infty }\leq \|\varphi _\omega \|_{L^\infty }\leq C\|\varphi _{\omega }\|_{BV}\leq CK({\omega })^{-1}$
, we obtain that
 $$ \begin{align*} |\mu_\omega(F_\omega)-m(F_{\omega}\mathcal L_{\sigma^{-n}\omega}^n\textbf{1})|&=\bigg|\int(h_\omega-\mathcal L^n_{\sigma^{-n}\omega}\textbf{1})F_ \omega\, dm\bigg|\\&\leq CK(\omega)^{-1}\int|h_\omega-\mathcal L^n_{\sigma^{-n}\omega}\textbf{1}|\,dm\\ &\leq K(\omega)^{-1}e^{-\unicode{x3bb} n}K(\sigma^{-n}\omega)\leq Ce^{-n(\unicode{x3bb}-{\varepsilon})}.\\[-37pt] \end{align*} $$
$$ \begin{align*} |\mu_\omega(F_\omega)-m(F_{\omega}\mathcal L_{\sigma^{-n}\omega}^n\textbf{1})|&=\bigg|\int(h_\omega-\mathcal L^n_{\sigma^{-n}\omega}\textbf{1})F_ \omega\, dm\bigg|\\&\leq CK(\omega)^{-1}\int|h_\omega-\mathcal L^n_{\sigma^{-n}\omega}\textbf{1}|\,dm\\ &\leq K(\omega)^{-1}e^{-\unicode{x3bb} n}K(\sigma^{-n}\omega)\leq Ce^{-n(\unicode{x3bb}-{\varepsilon})}.\\[-37pt] \end{align*} $$
Taking into account that
![]() $|\mu _\omega (F_\omega )|\leq 1$
, that
$|\mu _\omega (F_\omega )|\leq 1$
, that
![]() $|m(F_\omega {\mathcal L}_{\sigma ^{-n}\omega }^n\textbf {1})|=|m(F_{\omega }\circ T_{{\sigma }^{-n}{\omega }}^n)|\leq 1$
and that
$|m(F_\omega {\mathcal L}_{\sigma ^{-n}\omega }^n\textbf {1})|=|m(F_{\omega }\circ T_{{\sigma }^{-n}{\omega }}^n)|\leq 1$
and that
![]() $|\prod _{j}\alpha _j-\prod _j\beta _j|\leq \sum _j|\alpha _j-\beta _j|$
for all numbers
$|\prod _{j}\alpha _j-\prod _j\beta _j|\leq \sum _j|\alpha _j-\beta _j|$
for all numbers
![]() $\alpha _j,\beta $
so that
$\alpha _j,\beta $
so that
![]() $|{\alpha }_j|,|\beta _j|\leq 1$
, we get the following result directly from Corollary 3.7 and Lemma 3.8.
$|{\alpha }_j|,|\beta _j|\leq 1$
, we get the following result directly from Corollary 3.7 and Lemma 3.8.
Corollary 3.9. Let
![]() $b_j$
be the left end point of the block
$b_j$
be the left end point of the block
![]() $B_j$
. Let us also set
$B_j$
. Let us also set
![]() $r_j=d_j/3$
and
$r_j=d_j/3$
and
![]() $r_0=r_1$
. Then there exists a constant
$r_0=r_1$
. Then there exists a constant
![]() $A_1>0$
which does not depend on
$A_1>0$
which does not depend on
![]() ${\omega }$
or on the blocks so that in the notation of Corollary 3.7 and Lemma 3.8 we have
${\omega }$
or on the blocks so that in the notation of Corollary 3.7 and Lemma 3.8 we have
 $$ \begin{align*} \bigg|\int \prod_{j=1}^{m}G_j\,d\mu-\int\bigg(\prod_{j=0}^{d}m(\varphi_{{\omega},j}\mathcal L^{d_j}_{\sigma^{b_j-d_j}\omega}\textbf{1})\bigg)\,d\mathbb P(\omega)\bigg|\leq A_1\sum_{j=1}^{m-1}e^{-(\unicode{x3bb}-{\varepsilon})r_j}, \end{align*} $$
$$ \begin{align*} \bigg|\int \prod_{j=1}^{m}G_j\,d\mu-\int\bigg(\prod_{j=0}^{d}m(\varphi_{{\omega},j}\mathcal L^{d_j}_{\sigma^{b_j-d_j}\omega}\textbf{1})\bigg)\,d\mathbb P(\omega)\bigg|\leq A_1\sum_{j=1}^{m-1}e^{-(\unicode{x3bb}-{\varepsilon})r_j}, \end{align*} $$
where
 $$ \begin{align*} \varphi_{\omega,j}=\prod_{i\in B_j}\varphi_{\sigma^i\omega}\circ T_{\sigma^{b_j}\omega}^{i-b_j}. \end{align*} $$
$$ \begin{align*} \varphi_{\omega,j}=\prod_{i\in B_j}\varphi_{\sigma^i\omega}\circ T_{\sigma^{b_j}\omega}^{i-b_j}. \end{align*} $$
Now we observe that
![]() $m(\varphi _{{\omega },j}\mathcal L^{d_j}_{\sigma ^{n_j-d_j}\omega }\textbf {1})$
is a function of
$m(\varphi _{{\omega },j}\mathcal L^{d_j}_{\sigma ^{n_j-d_j}\omega }\textbf {1})$
is a function of
![]() $\xi _{b_j-r_j}\ldots \xi _{b_{j+1}-r_j}$
(that is, of the coordinates
$\xi _{b_j-r_j}\ldots \xi _{b_{j+1}-r_j}$
(that is, of the coordinates
![]() ${\omega }_{b_j-r_j}\ldots {\omega }_{b_{j+1}-r_j}$
). Namely, in distribution it can be written as
${\omega }_{b_j-r_j}\ldots {\omega }_{b_{j+1}-r_j}$
). Namely, in distribution it can be written as
for some measurable function
![]() $f_j$
. Since
$f_j$
. Since
![]() $ m(\varphi _{{\omega },j}\mathcal L^{d_j}_{\sigma ^{n_j-d_j}\omega }\textbf {1})=m(\varphi _{{\omega },j}\circ T_{\sigma ^{n_j-d_j}\omega }^{d_j}) $
and
$ m(\varphi _{{\omega },j}\mathcal L^{d_j}_{\sigma ^{n_j-d_j}\omega }\textbf {1})=m(\varphi _{{\omega },j}\circ T_{\sigma ^{n_j-d_j}\omega }^{d_j}) $
and
![]() $|\varphi _{{\omega },j}|\leq 1$
, we can ensure that
$|\varphi _{{\omega },j}|\leq 1$
, we can ensure that
![]() $|f_j|\leq 1$
. Using [Reference Hafouta25, (2.20)] and Corollary 3.9 we conclude that the following result holds.
$|f_j|\leq 1$
. Using [Reference Hafouta25, (2.20)] and Corollary 3.9 we conclude that the following result holds.
Corollary 3.10. Let
![]() $G_j$
,
$G_j$
,
![]() $1\leq j\leq m$
, be as in Corollary 3.7 (defined by some blocks
$1\leq j\leq m$
, be as in Corollary 3.7 (defined by some blocks
![]() $B_j$
with gaps
$B_j$
with gaps
![]() $d_j$
). There are constants
$d_j$
). There are constants
![]() $A>1$
and
$A>1$
and
![]() $\delta _0\in (0,1)$
which do not depend on the blocks so that
$\delta _0\in (0,1)$
which do not depend on the blocks so that
 $$ \begin{align*} \bigg|\int \bigg(\prod_{j=1}^{m}G_j\bigg)\,d\mu-\bigg(\prod_{j=1}^{m}\int G_j\,d\mu\bigg)\bigg|\leq A\sum_{j=1}^{m}(\delta_0^{r_j}+\alpha([r_j])). \end{align*} $$
$$ \begin{align*} \bigg|\int \bigg(\prod_{j=1}^{m}G_j\bigg)\,d\mu-\bigg(\prod_{j=1}^{m}\int G_j\,d\mu\bigg)\bigg|\leq A\sum_{j=1}^{m}(\delta_0^{r_j}+\alpha([r_j])). \end{align*} $$
All that is left is to notice that Corollary 3.10 is a reformulation of Proposition 3.4, using the notation of this section.
3.2 Limit theorems via the method of cumulants
3.2.1 The central limit theorem: proof of Theorem 2.14
First, by Proposition 3.4 we have that (3.2) holds true with the numbers
![]() $\varrho _{i,(1+{\delta })k}$
and
$\varrho _{i,(1+{\delta })k}$
and
![]() $\gamma _{\delta }(b,k)$
specified in Proposition 3.4. By taking
$\gamma _{\delta }(b,k)$
specified in Proposition 3.4. By taking
![]() $r=2$
,
$r=2$
,
![]() $A_1=\{0\}$
and
$A_1=\{0\}$
and
![]() $A_2=\{n\}$
in (3.2) we see that
$A_2=\{n\}$
in (3.2) we see that
for some
![]() ${\delta }\in (0,1)$
. Hence, if
${\delta }\in (0,1)$
. Hence, if
![]() $\sum n{\alpha }_n<\infty $
then
$\sum n{\alpha }_n<\infty $
then
![]() $\sum _n n|{\mathbb E}_\mu [\varphi \cdot \varphi ^n]|<\infty $
and the results concerning the asymptotic variance
$\sum _n n|{\mathbb E}_\mu [\varphi \cdot \varphi ^n]|<\infty $
and the results concerning the asymptotic variance
![]() $s^2$
follow from the general theory of (weakly) stationary processes (see [Reference Ibragimov and Linnik34] and Lemma 3.11 below).
$s^2$
follow from the general theory of (weakly) stationary processes (see [Reference Ibragimov and Linnik34] and Lemma 3.11 below).
Now suppose that
![]() $s^2=\lim _{n\to \infty }(1/n)\mathrm {Var}_\mu (S_n)>0$
, where
$s^2=\lim _{n\to \infty }(1/n)\mathrm {Var}_\mu (S_n)>0$
, where
![]() $S_n=S_n\varphi $
. To prove the CLT and the convergence rate (2.19), by applying [Reference Saulis and Statulevicius49, Corollary 2.1], taking into account Theorem 3.1, we get the CLT and the rate (2.19) for
$S_n=S_n\varphi $
. To prove the CLT and the convergence rate (2.19), by applying [Reference Saulis and Statulevicius49, Corollary 2.1], taking into account Theorem 3.1, we get the CLT and the rate (2.19) for
![]() $S_n/\sqrt {\mathrm {Var}(S_n)}$
. To get the same rate for
$S_n/\sqrt {\mathrm {Var}(S_n)}$
. To get the same rate for
![]() $S_n/\sqrt n$
we need the following general fact from the theory of stationary real-valued sequences, which for the sake of convenience is stated as a lemma.
$S_n/\sqrt n$
we need the following general fact from the theory of stationary real-valued sequences, which for the sake of convenience is stated as a lemma.
Lemma 3.11. Let
![]() $Y_n$
be a centered weakly stationary sequence of square integrable random variables. Set
$Y_n$
be a centered weakly stationary sequence of square integrable random variables. Set
![]() $b_n={\mathbb E}[Y_0Y_n]$
and
$b_n={\mathbb E}[Y_0Y_n]$
and
![]() $S_n=\sum _{j=1}^nY_j$
. Suppose that
$S_n=\sum _{j=1}^nY_j$
. Suppose that
![]() $\sum _{k}k|b_k|<\infty $
. Then
$\sum _{k}k|b_k|<\infty $
. Then
 $$ \begin{align*} \lim_{n\to\infty}\frac 1n{\mathbb E}[S_n^2]=b_0+2\sum_{n\geq 1}b_n:=s^2 \end{align*} $$
$$ \begin{align*} \lim_{n\to\infty}\frac 1n{\mathbb E}[S_n^2]=b_0+2\sum_{n\geq 1}b_n:=s^2 \end{align*} $$
and
 $$ \begin{align*} \bigg|\frac1n{\mathbb E}[S_n^2]-s^2\bigg|\leq 2n^{-1}\sum_{k=1}^\infty k|b_k|. \end{align*} $$
$$ \begin{align*} \bigg|\frac1n{\mathbb E}[S_n^2]-s^2\bigg|\leq 2n^{-1}\sum_{k=1}^\infty k|b_k|. \end{align*} $$
Let us give a reminder of the short proof. We have
![]() $(1/n){\mathbb E}[S_n^2]\kern1.2pt{=}\kern1.2pt\sum _{k=1}^{n-1}(1\kern1.2pt{-}\kern1.2pt k/n)b_k\kern1.2pt{+}\kern1.2pt b_0$
and so
$(1/n){\mathbb E}[S_n^2]\kern1.2pt{=}\kern1.2pt\sum _{k=1}^{n-1}(1\kern1.2pt{-}\kern1.2pt k/n)b_k\kern1.2pt{+}\kern1.2pt b_0$
and so
 $$ \begin{align*} \bigg|\frac1n{\mathbb E}[S_n^2]-s^2\bigg|&=\bigg|2\sum_{k=n}^\infty b_k+2n^{-1}\sum_{k=1}^{n-1}kb_k\bigg|\\&\leq 2n^{-1}\bigg(\sum_{k=n}^\infty k|b_k|+\sum_{k=1}^{n-1}k|b_k|\bigg)\leq 2n^{-1}\sum_{k\geq 1}k|b_k|. \end{align*} $$
$$ \begin{align*} \bigg|\frac1n{\mathbb E}[S_n^2]-s^2\bigg|&=\bigg|2\sum_{k=n}^\infty b_k+2n^{-1}\sum_{k=1}^{n-1}kb_k\bigg|\\&\leq 2n^{-1}\bigg(\sum_{k=n}^\infty k|b_k|+\sum_{k=1}^{n-1}k|b_k|\bigg)\leq 2n^{-1}\sum_{k\geq 1}k|b_k|. \end{align*} $$
Using this lemma together with [Reference Hafouta and Kifer29, Lemma 3.3] with
![]() $a=2$
and that
$a=2$
and that
 $$ \begin{align*} \bigg\|\frac{S_n}{\sqrt{\mathrm{Var}(S_n)}}-\frac{S_n}{s\sqrt n}\bigg\|_{L^2} =\|S_n\|_{L^2}\bigg|\frac{1}{\sqrt{\mathrm{Var}(S_n)}}-\frac1{s\sqrt n}\bigg|\kern1.2pt{=}\kern1.2pt O(n^{1/2})\cdot O(n^{-3/2})\kern1.2pt{=}\kern1.2pt O(n^{-1}), \end{align*} $$
$$ \begin{align*} \bigg\|\frac{S_n}{\sqrt{\mathrm{Var}(S_n)}}-\frac{S_n}{s\sqrt n}\bigg\|_{L^2} =\|S_n\|_{L^2}\bigg|\frac{1}{\sqrt{\mathrm{Var}(S_n)}}-\frac1{s\sqrt n}\bigg|\kern1.2pt{=}\kern1.2pt O(n^{1/2})\cdot O(n^{-3/2})\kern1.2pt{=}\kern1.2pt O(n^{-1}), \end{align*} $$
we obtain (2.19).
3.2.2 A moderate-deviations principle, stretched exponential concentration inequalities and Rosenthal-type estimates: proof of Theorems 2.15–2.17
First, Theorem 2.15 follows from Theorem 3.1 and [Reference Saulis and Statulevicius49, Lemma 2.3]. The estimates (2.21) stated in Theorem 2.16 follow from Theorem 3.1 and [Reference Döring and Eichelsbacher15, Lemma 2.3] (which is a consequence of [Reference Saulis and Statulevicius49, Lemma 2.3]). The moderate-deviations principle stated in Theorem 2.16 follows from Theorem 3.1 and [Reference Döring and Eichelsbacher15, Theorem 1.1]. We note that the conditions of [Reference Saulis and Statulevicius49, Lemma 2.3], [Reference Döring and Eichelsbacher15, Lemma 2.3] and [Reference Döring and Eichelsbacher15, Theorem 1.1] are certain estimates on the growth rates (in k) of the cumulants
![]() $\Gamma _k(S_n)$
, and the role of Theorem 3.1 is that it shows that the conditions of all of these results are in force in the setup of this paper.
$\Gamma _k(S_n)$
, and the role of Theorem 3.1 is that it shows that the conditions of all of these results are in force in the setup of this paper.
3.3 A functional central limit theorem via the method of cumulants: proof of Theorem 2.19
Let us first show that the sequence
![]() ${\mathcal S}_n$
is tight. By Theorem 2.17 we have that
${\mathcal S}_n$
is tight. By Theorem 2.17 we have that
where
![]() $\|\cdot \|_4=\|\cdot \|_{L^4}$
, and therefore, using also stationarity and the Hölder inequality, we get that for all
$\|\cdot \|_4=\|\cdot \|_{L^4}$
, and therefore, using also stationarity and the Hölder inequality, we get that for all
![]() $t_1<t_2\leq r_1<r_2$
,
$t_1<t_2\leq r_1<r_2$
,
 $$ \begin{align*} {\mathbb E}[({\mathcal S}_{n}(r_2)-{\mathcal S}_{n}(r_1))^2({\mathcal S}_{n}(t_2)-{\mathcal S}_{n}(t_1))^2]&\leq \|{\mathcal S}_{n}(r_2)-{\mathcal S}_{n}(r_1)\|_4^2\|{\mathcal S}_{n}(t_2)-{\mathcal S}_{n}(t_1)\|_4^2\\ &\leq C\bigg(\frac{[r_2n]-[t_1n]}{n}\bigg)^2. \end{align*} $$
$$ \begin{align*} {\mathbb E}[({\mathcal S}_{n}(r_2)-{\mathcal S}_{n}(r_1))^2({\mathcal S}_{n}(t_2)-{\mathcal S}_{n}(t_1))^2]&\leq \|{\mathcal S}_{n}(r_2)-{\mathcal S}_{n}(r_1)\|_4^2\|{\mathcal S}_{n}(t_2)-{\mathcal S}_{n}(t_1)\|_4^2\\ &\leq C\bigg(\frac{[r_2n]-[t_1n]}{n}\bigg)^2. \end{align*} $$
Thus, by [Reference Billingsley10, Ch. 15],
![]() ${\mathcal S}_n(\cdot )$
is a tight sequence in the Skorokhod space
${\mathcal S}_n(\cdot )$
is a tight sequence in the Skorokhod space
![]() $D[0,1]$
.
$D[0,1]$
.
Now let us show that the finite-dimensional distributions converge. Let us fix some
![]() $t_1<t_2<\cdots <t_d$
. Set
$t_1<t_2<\cdots <t_d$
. Set
![]() $X_k=\varphi \circ \tau ^k$
. Next, let us recall the following general fact. Given a vector-valued sequence of random variables
$X_k=\varphi \circ \tau ^k$
. Next, let us recall the following general fact. Given a vector-valued sequence of random variables
![]() $Y_n=(Y_{1,n},\ldots , Y_{d,n})$
, by the multidimensional version of Levi’s theorem, in order to show that
$Y_n=(Y_{1,n},\ldots , Y_{d,n})$
, by the multidimensional version of Levi’s theorem, in order to show that
![]() $Y_n$
converges in distribution as
$Y_n$
converges in distribution as
![]() $n\to \infty $
towards a given random variable
$n\to \infty $
towards a given random variable
![]() ${\mathcal Z}$
, it is enough to show that for every
${\mathcal Z}$
, it is enough to show that for every
![]() $a\in {\mathbb R}^d$
we have
$a\in {\mathbb R}^d$
we have
Therefore, it is enough to show that any linear combination of
![]() $Y_{j,n}$
,
$Y_{j,n}$
,
![]() $j=1,2,\ldots , d$
, converges in distribution towards the corresponding linear combination of the coordinates of
$j=1,2,\ldots , d$
, converges in distribution towards the corresponding linear combination of the coordinates of
![]() ${\mathcal Z}$
. Returning to our problem, to obtain the appropriate convergence of the distribution of
${\mathcal Z}$
. Returning to our problem, to obtain the appropriate convergence of the distribution of
![]() $({\mathcal S}_n(it_j))_{j=1}^{d}$
it is enough to show that any linear combination of
$({\mathcal S}_n(it_j))_{j=1}^{d}$
it is enough to show that any linear combination of
![]() ${\mathcal S}_{n}(t_j)$
converges towards a centered normal random variable with an appropriate variance. More precisely, let
${\mathcal S}_{n}(t_j)$
converges towards a centered normal random variable with an appropriate variance. More precisely, let
![]() $a_1,\ldots , a_d\in {\mathbb R}$
. Then we need to show that
$a_1,\ldots , a_d\in {\mathbb R}$
. Then we need to show that
![]() $\sum _{j=1}^{d}a_j{\mathcal S}_{n}(t_j)$
converges in distribution towards a centered normal random variable with variance
$\sum _{j=1}^{d}a_j{\mathcal S}_{n}(t_j)$
converges in distribution towards a centered normal random variable with variance
 $$ \begin{align*} s^2\sum_{j=1}^d(a_j+\cdots+a_d)^2(t_j-t_{j-1}), \end{align*} $$
$$ \begin{align*} s^2\sum_{j=1}^d(a_j+\cdots+a_d)^2(t_j-t_{j-1}), \end{align*} $$
where
![]() $t_0=0$
and
$t_0=0$
and
![]() $s^2=\lim _{n\to \infty }\frac 1n{\mathbb E}[S_n^2]$
. We first notice that
$s^2=\lim _{n\to \infty }\frac 1n{\mathbb E}[S_n^2]$
. We first notice that
 $$ \begin{align*} \sum_{j=1}^da_j {\mathcal S}_{n}(t_j)=n^{-1/2}\sum_{j=1}^d(a_j+\cdots+a_d)(S_{[nt_j]}-S_{[nt_{j-1}]}), \end{align*} $$
$$ \begin{align*} \sum_{j=1}^da_j {\mathcal S}_{n}(t_j)=n^{-1/2}\sum_{j=1}^d(a_j+\cdots+a_d)(S_{[nt_j]}-S_{[nt_{j-1}]}), \end{align*} $$
where we set
![]() $t_0=0$
and
$t_0=0$
and
![]() $S_0=0$
. Thus, using stationarity, we have
$S_0=0$
. Thus, using stationarity, we have
 $$ \begin{align*} {\mathbb E}\bigg[\bigg(\sum_{j=1}^{d}a_j{\mathcal S}_{n}(t_j)\bigg)^2\bigg]&=n^{-1}\sum_{j=1}^d(a_j+\cdots+a_d)^2{\mathbb E}[S_{[nt_j]-[nt_{j-1}]}^2]\\ &\quad+2n^{-1}\sum_{1\leq j_1<j_2\leq d}(a_{j_1}+\cdots+a_{j_d})(a_{j_2}+\cdots+a_{j_d})\\ &\quad\times{\mathbb E}[(S_{[nt_{j_2}]}-S_{[nt_{j_2-1}]})(S_{[nt_{j_1}]}-S_{[nt_{j_1-1}]})]. \end{align*} $$
$$ \begin{align*} {\mathbb E}\bigg[\bigg(\sum_{j=1}^{d}a_j{\mathcal S}_{n}(t_j)\bigg)^2\bigg]&=n^{-1}\sum_{j=1}^d(a_j+\cdots+a_d)^2{\mathbb E}[S_{[nt_j]-[nt_{j-1}]}^2]\\ &\quad+2n^{-1}\sum_{1\leq j_1<j_2\leq d}(a_{j_1}+\cdots+a_{j_d})(a_{j_2}+\cdots+a_{j_d})\\ &\quad\times{\mathbb E}[(S_{[nt_{j_2}]}-S_{[nt_{j_2-1}]})(S_{[nt_{j_1}]}-S_{[nt_{j_1-1}]})]. \end{align*} $$
Now the first summand on the right-hand side above converges to
 $$ \begin{align*} s^2\sum_{j=1}^d(a_j+\cdots+a_d)^2(t_j-t_{j-1}), \end{align*} $$
$$ \begin{align*} s^2\sum_{j=1}^d(a_j+\cdots+a_d)^2(t_j-t_{j-1}), \end{align*} $$
while the second summand (the double sum) converges to
![]() $0$
because
$0$
because
![]() $|{\mathbb E}[\varphi \cdot \varphi \circ \tau ^n]|$
converges to
$|{\mathbb E}[\varphi \cdot \varphi \circ \tau ^n]|$
converges to
![]() $0$
stretched exponentially fast. Therefore, the asymptotic variance of
$0$
stretched exponentially fast. Therefore, the asymptotic variance of
![]() $\sum _{j=1}^{d}a_j{\mathcal S}_{n}(t_j)$
has the desired form. Now, let us consider the following array of random variables. Set
$\sum _{j=1}^{d}a_j{\mathcal S}_{n}(t_j)$
has the desired form. Now, let us consider the following array of random variables. Set
Then
 $$ \begin{align*} \sum_{j=1}^d(a_j+\cdots+a_d)(S_{[nt_j]}-S_{[nt_{j-1}]})= \sum_{j=1}^d(a_j+\cdots+a_d)\sum_{s=[nt_{j-1}]}^{[nt_j]-1}\varphi\circ\tau^s \end{align*} $$
$$ \begin{align*} \sum_{j=1}^d(a_j+\cdots+a_d)(S_{[nt_j]}-S_{[nt_{j-1}]})= \sum_{j=1}^d(a_j+\cdots+a_d)\sum_{s=[nt_{j-1}]}^{[nt_j]-1}\varphi\circ\tau^s \end{align*} $$
 $$ \begin{align*} =\sum_{j=1}^d(a_j+\cdots+a_d)\sum_{s=0}^{[nt_d]-1}{\mathbb I}([nt_{j-1}]\leq s<[nt_j])\varphi\circ\tau^s= \sum_{s=0}^{[nt_d]-1}Y_s. \end{align*} $$
$$ \begin{align*} =\sum_{j=1}^d(a_j+\cdots+a_d)\sum_{s=0}^{[nt_d]-1}{\mathbb I}([nt_{j-1}]\leq s<[nt_j])\varphi\circ\tau^s= \sum_{s=0}^{[nt_d]-1}Y_s. \end{align*} $$
On the other hand, arguing as in the proof of Theorem 3.1 (replacing each appearance of
![]() $\varphi \circ \tau ^k$
by
$\varphi \circ \tau ^k$
by
![]() $Y_k$
), we get the same kind of estimates on the cumulants of
$Y_k$
), we get the same kind of estimates on the cumulants of
 $$ \begin{align*} \tilde S_n:=\sum_{s=0}^{[nt_d]-1}Y_s, \end{align*} $$
$$ \begin{align*} \tilde S_n:=\sum_{s=0}^{[nt_d]-1}Y_s, \end{align*} $$
that is, there exists a constant
![]() $c_0$
which might depend on
$c_0$
which might depend on
![]() $t_j$
and
$t_j$
and
![]() $a_j$
such that for every k we have
$a_j$
such that for every k we have
Thus, by applying [Reference Saulis and Statulevicius49, Corollary 2.1] we get that
 $$ \begin{align*} \sum_{s=0}^{[nt_d]-1}Y_s^{(n,a_1\ldots a_d)}/w_n \end{align*} $$
$$ \begin{align*} \sum_{s=0}^{[nt_d]-1}Y_s^{(n,a_1\ldots a_d)}/w_n \end{align*} $$
converges towards the standard normal distribution, where
![]() $w_n$
is the standard deviation of the numerator. Note that, as we have shown,
$w_n$
is the standard deviation of the numerator. Note that, as we have shown,
![]() $w_n^2/n{\kern-1pt}\to{\kern-1pt} s^2{\kern-2pt}\sum _{j=1}^d(a_1{\kern-1pt}+\cdots +{\kern-1pt}a_d)^2(t_j{\kern-1pt}-{\kern-1pt}t_{j-1})$
, which is positive unless either
$w_n^2/n{\kern-1pt}\to{\kern-1pt} s^2{\kern-2pt}\sum _{j=1}^d(a_1{\kern-1pt}+\cdots +{\kern-1pt}a_d)^2(t_j{\kern-1pt}-{\kern-1pt}t_{j-1})$
, which is positive unless either
![]() $s=0$
or
$s=0$
or
![]() $ a_1=\cdots =a_d=0$
, which are both trivial cases. Thus, in any case we obtain the desired convergence of the linear combination
$ a_1=\cdots =a_d=0$
, which are both trivial cases. Thus, in any case we obtain the desired convergence of the linear combination
![]() $ \sum _{j=1}^d a_j{\mathcal S}_{n}(t_j) $
and the proof of Theorem 2.19 is complete.
$ \sum _{j=1}^d a_j{\mathcal S}_{n}(t_j) $
and the proof of Theorem 2.19 is complete.
4 Limit theorems via martingale approximation for
 $\phi $
- and
$\phi $
- and
 $\psi $
-mixing driving processes
$\psi $
-mixing driving processes
4.1 Some expectation estimates using mixing coefficients
In the course of the proof of Theorem 2.22 we will need the following two relatively simple lemmas.
Lemma 4.1. Let
![]() ${\mathcal G},{\mathcal H}$
be two sub-
${\mathcal G},{\mathcal H}$
be two sub-
![]() ${\sigma }$
-algebras of a given
${\sigma }$
-algebras of a given
![]() ${\sigma }$
-algebra on some space measure space. Let g be a real-valued bounded
${\sigma }$
-algebra on some space measure space. Let g be a real-valued bounded
![]() ${\mathcal G}$
-measurable function and h be an
${\mathcal G}$
-measurable function and h be an
![]() ${\mathcal H}$
-measurable real-valued integrable function. Then
${\mathcal H}$
-measurable real-valued integrable function. Then
Proof. By [Reference Bradley11, Ch. 4] we have
which clearly implies the lemma.
Lemma 4.2. Let
![]() ${\mathcal G},{\mathcal H}$
be two sub-
${\mathcal G},{\mathcal H}$
be two sub-
![]() ${\sigma }$
-algebras of a given
${\sigma }$
-algebras of a given
![]() ${\sigma }$
-algebra on some measure space. Let g a real-valued bounded
${\sigma }$
-algebra on some measure space. Let g a real-valued bounded
![]() ${\mathcal G}$
-measurable function and h be an
${\mathcal G}$
-measurable function and h be an
![]() ${\mathcal H}$
-measurable real-valued integrable function. Suppose also that
${\mathcal H}$
-measurable real-valued integrable function. Suppose also that
![]() $\psi =\psi ({\mathcal G},{\mathcal H})<1$
. Then
$\psi =\psi ({\mathcal G},{\mathcal H})<1$
. Then
where
![]() $C_{\psi }=(1-\psi )^{-1}$
.
$C_{\psi }=(1-\psi )^{-1}$
.
Proof. By [Reference Bradley11, Ch. 4] we have
Hence
Taking
![]() $h,g\geq 0$
, we get that
$h,g\geq 0$
, we get that
Thus,
Therefore, for non-negative functions we have
Now the general result follows by writing
![]() $h=h^+-h^{-}$
and
$h=h^+-h^{-}$
and
![]() $g=g^{+}-g^{-}$
, where
$g=g^{+}-g^{-}$
, where
![]() $h^{\pm }$
and
$h^{\pm }$
and
![]() $g^{\pm }$
are non-negative functions such that
$g^{\pm }$
are non-negative functions such that
![]() $h^{+}+h^{-}=|h|$
and
$h^{+}+h^{-}=|h|$
and
![]() $g^{+}+g^{-}=|g|$
, and using that both
$g^{+}+g^{-}=|g|$
, and using that both
![]() $(g,h)\to {\mathbb E}[g]{\mathbb E}[h]$
and
$(g,h)\to {\mathbb E}[g]{\mathbb E}[h]$
and
![]() $(g,h)\to {\mathbb E}[hg]$
are bilinear in
$(g,h)\to {\mathbb E}[hg]$
are bilinear in
![]() $(g,h)$
.
$(g,h)$
.
4.2 Convergence of the iterates of the transfer operator with respect to a sub-
 ${\sigma }$
-algebra
${\sigma }$
-algebra
Let
![]() ${\mathcal F}_0$
be the
${\mathcal F}_0$
be the
![]() $\sigma $
-algebra generated by the map
$\sigma $
-algebra generated by the map
![]() $\pi ({\omega },x)=(({\omega }_j)_{j\geq 0},x)$
, namely, the one generated by
$\pi ({\omega },x)=(({\omega }_j)_{j\geq 0},x)$
, namely, the one generated by
![]() ${\mathcal B}$
and the coordinates with non-negative indexes in the
${\mathcal B}$
and the coordinates with non-negative indexes in the
![]() ${\omega }$
direction. Then
${\omega }$
direction. Then
![]() $(\tau ^{-k}{\mathcal F}_0)_{k\geq 0}$
is a decreasing sequence of
$(\tau ^{-k}{\mathcal F}_0)_{k\geq 0}$
is a decreasing sequence of
![]() ${\sigma }$
-algebras and
${\sigma }$
-algebras and
![]() $\tau ^{-k}{\mathcal F}_0$
is generated by
$\tau ^{-k}{\mathcal F}_0$
is generated by
![]() $\tau ^k$
and the coordinates
$\tau ^k$
and the coordinates
![]() ${\omega }_{j}$
for
${\omega }_{j}$
for
![]() $j\geq k$
. In particular,
$j\geq k$
. In particular,
![]() $\tau $
preserves
$\tau $
preserves
![]() ${\mathcal F}_0$
.
${\mathcal F}_0$
.
Next, let us define a transfer operator with respect to
![]() ${\mathcal F}_0$
. For each function
${\mathcal F}_0$
. For each function
![]() $g\in L^1(\mu )$
there is a unique
$g\in L^1(\mu )$
there is a unique
![]() ${\mathcal F}_0$
-measurable function G such that
${\mathcal F}_0$
-measurable function G such that
Let us define
![]() ${\mathcal K} g=G$
, where we formally set G to be
${\mathcal K} g=G$
, where we formally set G to be
![]() $0$
outside the image of
$0$
outside the image of
![]() $\tau $
(if
$\tau $
(if
![]() $\tau $
is not onto). Then
$\tau $
is not onto). Then
Notice that for
![]() $g\in L^1({\Omega }\times X,{\mathcal F}_0,\mu ), f\in L^\infty ({\Omega }\times X,{\mathcal F}_0,\mu )$
we have
$g\in L^1({\Omega }\times X,{\mathcal F}_0,\mu ), f\in L^\infty ({\Omega }\times X,{\mathcal F}_0,\mu )$
we have
and therefore
![]() ${\mathcal K}$
can also be defined using the usual duality relation with respect to the above
${\mathcal K}$
can also be defined using the usual duality relation with respect to the above
![]() ${\sigma }$
-algebra. That is, it is the transfer operator of
${\sigma }$
-algebra. That is, it is the transfer operator of
![]() $\tau $
with respect to
$\tau $
with respect to
![]() $({\Omega }\times X,{\mathcal F}_0,\mu )$
.
$({\Omega }\times X,{\mathcal F}_0,\mu )$
.
The proof of Theorems 2.21 and 2.22 is based on the following result.
Proposition 4.3. Under the assumptions of Theorems 2.21 and 2.22, and when
![]() $\mu (\varphi )=0$
, we have the following assertions.
$\mu (\varphi )=0$
, we have the following assertions.
-
(i) We have
(4.1)Moreover, if $$ \begin{align} \|{\mathcal K}^{\,n}\varphi\|_{L^\infty}\leq C(e^{-({\unicode{x3bb}}-2{\varepsilon})n/2}+\psi_{[n/2]}):=C\gamma_{2,n}. \end{align} $$
$$ \begin{align} \|{\mathcal K}^{\,n}\varphi\|_{L^\infty}\leq C(e^{-({\unicode{x3bb}}-2{\varepsilon})n/2}+\psi_{[n/2]}):=C\gamma_{2,n}. \end{align} $$
 $h_{\omega } \geq c^{-1}>0$
for some constant
$h_{\omega } \geq c^{-1}>0$
for some constant
 $c>1$
then (4.2)Here
$c>1$
then (4.2)Here $$ \begin{align} \|{\mathcal K}^{\,n}\varphi\|_{L^\infty}\leq Cc(e^{-({\unicode{x3bb}}-2{\varepsilon})n/2}+\phi_{[n/2],R}):=C\gamma_{1,n}. \end{align} $$
$$ \begin{align} \|{\mathcal K}^{\,n}\varphi\|_{L^\infty}\leq Cc(e^{-({\unicode{x3bb}}-2{\varepsilon})n/2}+\phi_{[n/2],R}):=C\gamma_{1,n}. \end{align} $$
 $C=C_{\varphi }$
is a constant having the form
$C=C_{\varphi }$
is a constant having the form
 $C_{\varphi }=AC_{\mathrm {v}}\operatorname {\mathrm {esssup}}_{{\omega }\in {\Omega }}(K({\omega })^2\|\varphi _{\omega }\|_{BV})$
, where A is an absolute constant and
$C_{\varphi }=AC_{\mathrm {v}}\operatorname {\mathrm {esssup}}_{{\omega }\in {\Omega }}(K({\omega })^2\|\varphi _{\omega }\|_{BV})$
, where A is an absolute constant and
 $C_0$
is any constant satisfying
$C_0$
is any constant satisfying
 $\|g\|_{L^\infty }\leq C_0\|g\|_{BV}$
and
$\|g\|_{L^\infty }\leq C_0\|g\|_{BV}$
and
 $\|fg\|_{BV}\leq C_0\|g\|_{BV}\|f\|_{BV}$
for all functions
$\|fg\|_{BV}\leq C_0\|g\|_{BV}\|f\|_{BV}$
for all functions
 $g,f:X\to {\mathbb C}$
.
$g,f:X\to {\mathbb C}$
.
-
(ii) We have
If $$ \begin{align*} \|{\mathcal K}^i(\varphi {\mathcal K}^j\varphi)-\mu({\mathcal K}^i(\varphi {\mathcal K}^j\varphi))\|_{L^\infty}\leq C\gamma_{2,\max(i,j)}. \end{align*} $$
$$ \begin{align*} \|{\mathcal K}^i(\varphi {\mathcal K}^j\varphi)-\mu({\mathcal K}^i(\varphi {\mathcal K}^j\varphi))\|_{L^\infty}\leq C\gamma_{2,\max(i,j)}. \end{align*} $$
 $h_{\omega } \geq c^{-1}>0$
for some constant
$h_{\omega } \geq c^{-1}>0$
for some constant
 $c>1$
then
$c>1$
then  $$ \begin{align*} \|{\mathcal K}^i(\varphi {\mathcal K}^j\varphi)-\mu({\mathcal K}^i(\varphi {\mathcal K}^j\varphi))\|_{L^\infty}\leq Cc\gamma_{1,\max(i,j)}. \end{align*} $$
$$ \begin{align*} \|{\mathcal K}^i(\varphi {\mathcal K}^j\varphi)-\mu({\mathcal K}^i(\varphi {\mathcal K}^j\varphi))\|_{L^\infty}\leq Cc\gamma_{1,\max(i,j)}. \end{align*} $$
Proof of Theorems 2.21 and 2.22 based on Proposition 4.3.
First, Theorem 2.21(i) follows since if we set
![]() $\chi =\sum _{n=1}^\infty K^n\varphi $
and
$\chi =\sum _{n=1}^\infty K^n\varphi $
and
![]() $u=\varphi +\chi \circ \tau -\chi $
, then
$u=\varphi +\chi \circ \tau -\chi $
, then
![]() $\|\chi \|_{L^\infty }<\infty $
and
$\|\chi \|_{L^\infty }<\infty $
and
![]() $(u\circ \tau ^n)$
is a reverse martingale difference with respect to the reverse filtration
$(u\circ \tau ^n)$
is a reverse martingale difference with respect to the reverse filtration
![]() $\{\tau ^{-n}{\mathcal F}_0\}$
. Moreover, the differences
$\{\tau ^{-n}{\mathcal F}_0\}$
. Moreover, the differences
![]() $u\circ \tau ^n$
are uniformly bounded (as
$u\circ \tau ^n$
are uniformly bounded (as
![]() $\chi $
and
$\chi $
and
![]() $\varphi $
are in
$\varphi $
are in
![]() $L^\infty $
). Thus, by the Azuma–Hoeffding inequality, for every
$L^\infty $
). Thus, by the Azuma–Hoeffding inequality, for every
![]() ${\beta }>0$
, we have
${\beta }>0$
, we have
Now the proof proceeds by using the Chernoff bounding method. By the Markov inequality for all
![]() $t>0$
we have
$t>0$
we have
 $$ \begin{align*} \mu\bigg\{\sum_{j=0}^{n-1}u\circ\tau^j\geq tn\bigg\}\leq e^{-{\beta} tn}e^{{\beta}^2n\|u\|_{L^\infty}^2}. \end{align*} $$
$$ \begin{align*} \mu\bigg\{\sum_{j=0}^{n-1}u\circ\tau^j\geq tn\bigg\}\leq e^{-{\beta} tn}e^{{\beta}^2n\|u\|_{L^\infty}^2}. \end{align*} $$
Taking
![]() ${\beta }={\beta }_t={t}/{2\|u\|_{L^\infty }}$
and replacing u with
${\beta }={\beta }_t={t}/{2\|u\|_{L^\infty }}$
and replacing u with
![]() $-u$
, we get that
$-u$
, we get that
 $$ \begin{align*} \mu\bigg\{\pm\sum_{j=0}^{n-1}u\circ\tau^j\geq tn\bigg\}\leq e^{-{nt^2}/{4\|u\|_{L^\infty}}}. \end{align*} $$
$$ \begin{align*} \mu\bigg\{\pm\sum_{j=0}^{n-1}u\circ\tau^j\geq tn\bigg\}\leq e^{-{nt^2}/{4\|u\|_{L^\infty}}}. \end{align*} $$
The proof of Theorem 2.21(i) is completed now by noticing that
 $$ \begin{align} \bigg\|S_n\varphi-\sum_{j=0}^{n-1}u\circ\tau^j\bigg\|_{L^\infty}=\|\chi-\chi\circ\tau^n\|_{L ^\infty}\leq 2\|\chi\|_{L^\infty}. \end{align} $$
$$ \begin{align} \bigg\|S_n\varphi-\sum_{j=0}^{n-1}u\circ\tau^j\bigg\|_{L^\infty}=\|\chi-\chi\circ\tau^n\|_{L ^\infty}\leq 2\|\chi\|_{L^\infty}. \end{align} $$
Next, the proof of Theorem 2.21(ii) is completed by applying [Reference Merlevéde, Peligrad and Utev45, Proposition 7] with the reverse martingale
![]() $(u\circ \tau ^n)$
and using (4.3).
$(u\circ \tau ^n)$
and using (4.3).
In order to prove Theorem 2.22, we apply [Reference Cuny and Merlevede13, Theorem 3.2] with the bounded function
![]() $\varphi $
and the probability-preserving system
$\varphi $
and the probability-preserving system
![]() $({\Omega }\times X,{\mathcal F}_0,\mu ,\tau )$
, whose transfer operator is
$({\Omega }\times X,{\mathcal F}_0,\mu ,\tau )$
, whose transfer operator is
![]() ${\mathcal K}$
. Now, since we have assumed that
${\mathcal K}$
. Now, since we have assumed that
![]() $\mu (\varphi )=0$
, in order for the conditions of [Reference Cuny and Merlevede13, Theorem 3.2] to be in force we need the estimates
$\mu (\varphi )=0$
, in order for the conditions of [Reference Cuny and Merlevede13, Theorem 3.2] to be in force we need the estimates
 $$ \begin{align*} &\kern65pt\sum_{n\geq 2}n^{5/2}(\log n)^3\|{\mathcal K}\varphi\|_{L^4(\mu)}^4<\infty,\\&\kern72pt\sum_{n\geq 2}n(\log n)^3\|{\mathcal K}\varphi\|_{L^2(\mu)}^2<\infty,\\&\sum_{n\geq 2}\frac{(\log n)^3}{n^2}\bigg(\sum_{i=1}^{n}\sum_{j=0}^{n-i}\|{\mathcal K}^i(\varphi {\mathcal K}^j(\varphi))-\mu(\varphi {\mathcal K}^j(\varphi))\|_{L^2(\mu)}\bigg)^2<\infty \end{align*} $$
$$ \begin{align*} &\kern65pt\sum_{n\geq 2}n^{5/2}(\log n)^3\|{\mathcal K}\varphi\|_{L^4(\mu)}^4<\infty,\\&\kern72pt\sum_{n\geq 2}n(\log n)^3\|{\mathcal K}\varphi\|_{L^2(\mu)}^2<\infty,\\&\sum_{n\geq 2}\frac{(\log n)^3}{n^2}\bigg(\sum_{i=1}^{n}\sum_{j=0}^{n-i}\|{\mathcal K}^i(\varphi {\mathcal K}^j(\varphi))-\mu(\varphi {\mathcal K}^j(\varphi))\|_{L^2(\mu)}\bigg)^2<\infty \end{align*} $$
to hold. These three conditions are verified by Proposition 4.3 and the mixing rates specified in the formulation of Theorem 2.22, and the proof of Theorem 2.22 is complete.
Proof of Proposition 4.3.
(i) Since
![]() $L^\infty (\mu )$
is the dual of
$L^\infty (\mu )$
is the dual of
![]() $L^1(\mu )$
, and
$L^1(\mu )$
, and
![]() $\varphi $
and
$\varphi $
and
![]() ${\mathcal K}^{\,n}\varphi $
are
${\mathcal K}^{\,n}\varphi $
are
![]() ${\mathcal F}_0$
-measurable, it is enough to show that, for every
${\mathcal F}_0$
-measurable, it is enough to show that, for every
![]() $g\in L^1({\Omega }\times X,{\mathcal F}_0,\mu )$
such that
$g\in L^1({\Omega }\times X,{\mathcal F}_0,\mu )$
such that
![]() $\|g\|_{L^1}\leq 1$
, we have
$\|g\|_{L^1}\leq 1$
, we have
 $$ \begin{align*} \bigg|\int g\cdot({\mathcal K}^{\,n}\varphi)\,d\mu\bigg|\leq\gamma_n\|g\|_{L^1(\mu)}, \end{align*} $$
$$ \begin{align*} \bigg|\int g\cdot({\mathcal K}^{\,n}\varphi)\,d\mu\bigg|\leq\gamma_n\|g\|_{L^1(\mu)}, \end{align*} $$
where
![]() $\gamma _n$
is one of the desired upper bounds. To achieve that let us first note that
$\gamma _n$
is one of the desired upper bounds. To achieve that let us first note that
![]() ${\mathcal K}^{\,n}$
is the dual of the restriction of the Koopman operator
${\mathcal K}^{\,n}$
is the dual of the restriction of the Koopman operator
![]() $f\to f\circ \tau ^n$
acting on
$f\to f\circ \tau ^n$
acting on
![]() ${\mathcal F}_0$
-measurable functions. Thus,
${\mathcal F}_0$
-measurable functions. Thus,
 $$ \begin{align} \int g\cdot({\mathcal K}^{\,n}\varphi)\,d\mu=\int \varphi\cdot (g\circ\tau^n) \,d\mu= \int\bigg(\int\varphi_{{\omega}}\cdot (g_{\sigma^n{\omega} }\circ T_{\omega}^n)\, d\mu_{\omega}\bigg)\,d{\mathbb P}({\omega}) \end{align} $$
$$ \begin{align} \int g\cdot({\mathcal K}^{\,n}\varphi)\,d\mu=\int \varphi\cdot (g\circ\tau^n) \,d\mu= \int\bigg(\int\varphi_{{\omega}}\cdot (g_{\sigma^n{\omega} }\circ T_{\omega}^n)\, d\mu_{\omega}\bigg)\,d{\mathbb P}({\omega}) \end{align} $$
 $$ \begin{align*} \kern-2pt=\int\bigg(\int (L_{\omega}^n\varphi_{{\omega}})\cdot g_{{\sigma}^n{\omega}}\, d\mu_{\sigma^n{\omega}}\bigg)\,d{\mathbb P}({\omega}).\qquad\,\quad \end{align*} $$
$$ \begin{align*} \kern-2pt=\int\bigg(\int (L_{\omega}^n\varphi_{{\omega}})\cdot g_{{\sigma}^n{\omega}}\, d\mu_{\sigma^n{\omega}}\bigg)\,d{\mathbb P}({\omega}).\qquad\,\quad \end{align*} $$
Now, using (2.14) and that
![]() $\|\varphi \|_{K}=\operatorname {\mathrm {esssup}}_{{\omega }\in {\Omega }}(K({\omega })\|\varphi _{\omega }\|_{BV})<\infty $
, we get that
$\|\varphi \|_{K}=\operatorname {\mathrm {esssup}}_{{\omega }\in {\Omega }}(K({\omega })\|\varphi _{\omega }\|_{BV})<\infty $
, we get that
Hence, using also the
![]() ${\sigma }$
-invariance of
${\sigma }$
-invariance of
![]() ${\mathbb P}$
,
${\mathbb P}$
,
where
![]() $|I|\leq Ce^{-{\unicode{x3bb} } n}\|g\|_{L^1(\mu )}$
. Next, let us write
$|I|\leq Ce^{-{\unicode{x3bb} } n}\|g\|_{L^1(\mu )}$
. Next, let us write
By (2.10) we have
Observe next that since
![]() $\|1/h_{\omega }\|_{BV}\leq K({\omega })$
we have
$\|1/h_{\omega }\|_{BV}\leq K({\omega })$
we have
for every function g, and recall that
![]() $K(\sigma ^n{\omega })\leq K({\omega })e^{{\varepsilon } n}$
. Combining this with the previous estimates, we get that
$K(\sigma ^n{\omega })\leq K({\omega })e^{{\varepsilon } n}$
. Combining this with the previous estimates, we get that
Therefore,
where
![]() $|I|\leq Ce^{-{\unicode{x3bb} } n}\|g\|_{L^1(\mu )}$
and
$|I|\leq Ce^{-{\unicode{x3bb} } n}\|g\|_{L^1(\mu )}$
and
![]() $|J|\leq C'e^{-({\unicode{x3bb} }-3{\varepsilon })n/2}\|g\|_{L^1(\mu )}$
and we have used that
$|J|\leq C'e^{-({\unicode{x3bb} }-3{\varepsilon })n/2}\|g\|_{L^1(\mu )}$
and we have used that
![]() $K({\omega })^2\|\varphi _{\omega }\|_{BV}$
is bounded.
$K({\omega })^2\|\varphi _{\omega }\|_{BV}$
is bounded.
Next, using (2.10) and that
![]() $K({\omega })$
is tempered, we have
$K({\omega })$
is tempered, we have
![]() $h_{\omega }=\lim _{n\to \infty }{\mathcal L}_{\sigma ^{-n}{\omega }}^n\textbf {1}$
, and therefore
$h_{\omega }=\lim _{n\to \infty }{\mathcal L}_{\sigma ^{-n}{\omega }}^n\textbf {1}$
, and therefore
![]() $h_{\omega }$
depends only on the coordinates
$h_{\omega }$
depends only on the coordinates
![]() ${\omega }_j$
for
${\omega }_j$
for
![]() $j\leq 0$
. Thus,
$j\leq 0$
. Thus,
for some measurable function F so that
![]() $|F|\leq \|\varphi \|_{L^1(\mu )}$
. Observe also that the random variable
$|F|\leq \|\varphi \|_{L^1(\mu )}$
. Observe also that the random variable
depends only on
![]() ${\omega }_j, j\geq [n/2]$
, since
${\omega }_j, j\geq [n/2]$
, since
![]() $g_{\omega }(x)$
is a function of x and
$g_{\omega }(x)$
is a function of x and
![]() ${\omega }_j, j\geq 0$
(that is, it factors through
${\omega }_j, j\geq 0$
(that is, it factors through
![]() $\pi _0$
). In the case where
$\pi _0$
). In the case where
![]() $h_{\omega }\geq c^{-1}>0$
for some constant
$h_{\omega }\geq c^{-1}>0$
for some constant
![]() $c>0$
we have
$c>0$
we have
Thus, using also Lemma 4.1, we see that there is a constant
![]() $C>0$
so that
$C>0$
so that
 $$ \begin{align*} &\bigg|\!\int \mu_{\omega}(\varphi_{{\omega}})m(g_{{\sigma}^n{\omega}}{\mathcal L}_{\sigma^{[n/2}]{\omega}}^{n-[n/2]}\textbf{1})\,d{\mathbb P}({\omega})\bigg|\\&\quad\leq C\phi_{[n/2],R}\int|G_n({\omega})|\,d{\mathbb P}({\omega})\leq cC\phi_{[n/2],R}\|g\|_{L^1(\mu)}, \end{align*} $$
$$ \begin{align*} &\bigg|\!\int \mu_{\omega}(\varphi_{{\omega}})m(g_{{\sigma}^n{\omega}}{\mathcal L}_{\sigma^{[n/2}]{\omega}}^{n-[n/2]}\textbf{1})\,d{\mathbb P}({\omega})\bigg|\\&\quad\leq C\phi_{[n/2],R}\int|G_n({\omega})|\,d{\mathbb P}({\omega})\leq cC\phi_{[n/2],R}\|g\|_{L^1(\mu)}, \end{align*} $$
where we have taken into account that
![]() $\int \mu _{\omega }(\varphi _{\omega })\,d{\mathbb P}({\omega })=\mu (\varphi )=0$
. This, together with (4.6) and the previous estimates on I and J, proves (4.2).
$\int \mu _{\omega }(\varphi _{\omega })\,d{\mathbb P}({\omega })=\mu (\varphi )=0$
. This, together with (4.6) and the previous estimates on I and J, proves (4.2).
To prove (4.1), we first use (4.5) in order to obtain that
Taking into account that
we conclude that
![]() $G_n({\omega })\mu _{{\omega }}(\varphi _{\omega })$
is integrable. We would now like to apply Lemma 4.2, but the problem is that
$G_n({\omega })\mu _{{\omega }}(\varphi _{\omega })$
is integrable. We would now like to apply Lemma 4.2, but the problem is that
![]() $G_n$
is not bounded. To overcome that, for each
$G_n$
is not bounded. To overcome that, for each
![]() $M>0$
set
$M>0$
set
![]() $G_n^{(M)}({\omega })=G_n({\omega }){\mathbb I}(|G_n({\omega })|\leq M)$
. Then, since
$G_n^{(M)}({\omega })=G_n({\omega }){\mathbb I}(|G_n({\omega })|\leq M)$
. Then, since
![]() $G_n({\omega })\mu _{{\omega }}(\varphi _{\omega })$
is integrable, by the dominated convergence theorem we have
$G_n({\omega })\mu _{{\omega }}(\varphi _{\omega })$
is integrable, by the dominated convergence theorem we have
Now, taking n so that
![]() $\psi _{[n/2]}\leq 1/2$
and using that
$\psi _{[n/2]}\leq 1/2$
and using that
![]() $\mu (\varphi )=0$
, we get from Lemma 4.2 that
$\mu (\varphi )=0$
, we get from Lemma 4.2 that
 $$ \begin{align*} \bigg|\int \mu_{\omega}(\varphi_{\omega})G_n^{(M)}({\omega})\,d{\mathbb P}({\omega})\bigg|&\leq2\bigg(\int |G_n^{(M)}({\omega})\mu_{\omega}(\varphi_{\omega})|\,d{\mathbb P}({\omega})\bigg)\psi_{[n/2]}\\&\leq 2\bigg(\int |G_n({\omega})\mu_{\omega}(\varphi_{\omega})|\,d{\mathbb P}({\omega})\bigg)\psi_{[n/2]}. \end{align*} $$
$$ \begin{align*} \bigg|\int \mu_{\omega}(\varphi_{\omega})G_n^{(M)}({\omega})\,d{\mathbb P}({\omega})\bigg|&\leq2\bigg(\int |G_n^{(M)}({\omega})\mu_{\omega}(\varphi_{\omega})|\,d{\mathbb P}({\omega})\bigg)\psi_{[n/2]}\\&\leq 2\bigg(\int |G_n({\omega})\mu_{\omega}(\varphi_{\omega})|\,d{\mathbb P}({\omega})\bigg)\psi_{[n/2]}. \end{align*} $$
Using also (4.7) and that
![]() $\text {esssup}_{{\omega }\in {\Omega }}(\|\varphi _{\omega }\|_{BV}K({\omega })^2)<\infty $
, we conclude that
$\text {esssup}_{{\omega }\in {\Omega }}(\|\varphi _{\omega }\|_{BV}K({\omega })^2)<\infty $
, we conclude that
 $$ \begin{align*} \bigg|\int \mu_{\omega}(\varphi_{\omega})G_n({\omega})\,d{\mathbb P}({\omega})\bigg|\leq 2(\operatorname{\mathrm{esssup}}_{{\omega}\in{\Omega}}(K({\omega})^2\|\varphi_{\omega}\|_{BV}))C'\|g\|_{L^1}\psi_{[n/2]} \end{align*} $$
$$ \begin{align*} \bigg|\int \mu_{\omega}(\varphi_{\omega})G_n({\omega})\,d{\mathbb P}({\omega})\bigg|\leq 2(\operatorname{\mathrm{esssup}}_{{\omega}\in{\Omega}}(K({\omega})^2\|\varphi_{\omega}\|_{BV}))C'\|g\|_{L^1}\psi_{[n/2]} \end{align*} $$
and (4.1) follows (using also (4.6)).
(ii) First, since
![]() ${\mathcal K}$
weakly contracts the
${\mathcal K}$
weakly contracts the
![]() $L^\infty $
norm (being defined through conditional expectations) and
$L^\infty $
norm (being defined through conditional expectations) and
![]() $\varphi $
is bounded we have
$\varphi $
is bounded we have
This, together with Proposition 4.3(i), provides the desired estimate when
![]() $j\geq i$
. The estimate in the case
$j\geq i$
. The estimate in the case
![]() $i>j$
is found similarly to the proof of (i). Let
$i>j$
is found similarly to the proof of (i). Let
![]() $g\in L^1({\Omega }\times X,\mu ,{\mathcal F}_0)$
. Let us first show that
$g\in L^1({\Omega }\times X,\mu ,{\mathcal F}_0)$
. Let us first show that
where
![]() $|I|\leq C_2e^{-{\unicode{x3bb} } i}$
, in which
$|I|\leq C_2e^{-{\unicode{x3bb} } i}$
, in which
![]() $C_2$
is some constant.
$C_2$
is some constant.
In order to prove (4.8), using that
![]() ${\mathcal K}$
satisfies the duality relation and the disintegration
${\mathcal K}$
satisfies the duality relation and the disintegration
![]() $\mu =\int \mu _{\omega } \,d{\mathbb P}({\omega })$
, we first have that
$\mu =\int \mu _{\omega } \,d{\mathbb P}({\omega })$
, we first have that
 $$ \begin{align} \int {\mathcal K}^i(\varphi {\mathcal K}^j\varphi)g\,d\mu&=\int (\varphi {\mathcal K}^j\varphi)\cdot g\circ\tau^i\,d\mu= \int {\mathcal K}^j\varphi\cdot(\varphi\cdot (g\circ\tau^i))\,d\mu\nonumber\\&=\int (\varphi\cdot(\varphi\circ\tau^j))\cdot g\circ\tau^{i+j}\,d\mu\nonumber\\ &=\int\bigg (\int \varphi_{\omega}\cdot (\varphi_{\sigma^j{\omega}}\circ T_{\omega}^{j})\cdot (g_{\sigma^{i+j}{\omega}}\circ T_{\omega}^{i+j})\,d\mu_{\omega}\bigg)\,d{\mathbb P}({\omega})\\ &=\int\bigg(\int L^{i+j}_{\omega}(\varphi_{\omega} \cdot (\varphi_{\sigma^j{\omega}}\circ T_{\omega}^j))g_{\sigma^{i+j}{\omega}}\,d\mu_{\sigma^{i+j}{\omega}}\bigg)\,d{\mathbb P}({\omega}).\nonumber \end{align} $$
$$ \begin{align} \int {\mathcal K}^i(\varphi {\mathcal K}^j\varphi)g\,d\mu&=\int (\varphi {\mathcal K}^j\varphi)\cdot g\circ\tau^i\,d\mu= \int {\mathcal K}^j\varphi\cdot(\varphi\cdot (g\circ\tau^i))\,d\mu\nonumber\\&=\int (\varphi\cdot(\varphi\circ\tau^j))\cdot g\circ\tau^{i+j}\,d\mu\nonumber\\ &=\int\bigg (\int \varphi_{\omega}\cdot (\varphi_{\sigma^j{\omega}}\circ T_{\omega}^{j})\cdot (g_{\sigma^{i+j}{\omega}}\circ T_{\omega}^{i+j})\,d\mu_{\omega}\bigg)\,d{\mathbb P}({\omega})\\ &=\int\bigg(\int L^{i+j}_{\omega}(\varphi_{\omega} \cdot (\varphi_{\sigma^j{\omega}}\circ T_{\omega}^j))g_{\sigma^{i+j}{\omega}}\,d\mu_{\sigma^{i+j}{\omega}}\bigg)\,d{\mathbb P}({\omega}).\nonumber \end{align} $$
Next, since
![]() $L_{\omega }^n(f\circ T_{\omega }^n)=f$
for every function f and n, we have
$L_{\omega }^n(f\circ T_{\omega }^n)=f$
for every function f and n, we have
By (2.14) we have
In particular,
for some constant C. Since
![]() $\|uv\|_{BV}\leq C_0\|u\|_{BV}\|v\|_{BV}$
for every pair of functions
$\|uv\|_{BV}\leq C_0\|u\|_{BV}\|v\|_{BV}$
for every pair of functions
![]() $u,v$
, we have
$u,v$
, we have
Thus by (2.14),
 $$ \begin{align*} &\|L_{\sigma^j{\omega}}^i(\varphi_{\sigma^j{\omega}}L_{{\omega}}^j\varphi_{\omega})-\mu_{\sigma^j{\omega}}(\varphi_{\sigma^j{\omega}}L_{{\omega}}^j\varphi_{\omega})\|_{BV}\\ &\quad\leq C_0CK({\omega})K(\sigma^j{\omega})\|\varphi_{\omega}\|_{BV}\|\varphi_{\sigma^j{\omega}}\|_{BV} e^{-{\unicode{x3bb}} i}\leq C_0C\|\varphi\|_{K}^2e^{-{\unicode{x3bb}} i}, \end{align*} $$
$$ \begin{align*} &\|L_{\sigma^j{\omega}}^i(\varphi_{\sigma^j{\omega}}L_{{\omega}}^j\varphi_{\omega})-\mu_{\sigma^j{\omega}}(\varphi_{\sigma^j{\omega}}L_{{\omega}}^j\varphi_{\omega})\|_{BV}\\ &\quad\leq C_0CK({\omega})K(\sigma^j{\omega})\|\varphi_{\omega}\|_{BV}\|\varphi_{\sigma^j{\omega}}\|_{BV} e^{-{\unicode{x3bb}} i}\leq C_0C\|\varphi\|_{K}^2e^{-{\unicode{x3bb}} i}, \end{align*} $$
where
![]() $\|\varphi \|_K=\operatorname {\mathrm {esssup}}_{{\omega }\in {\Omega }}(K({\omega })\|\varphi _{\omega }\|_{BV})$
. Observe next that
$\|\varphi \|_K=\operatorname {\mathrm {esssup}}_{{\omega }\in {\Omega }}(K({\omega })\|\varphi _{\omega }\|_{BV})$
. Observe next that
The desired inequality (4.8) follows from the above estimates.
Observe that the function
![]() $\mu _{{\omega }}(\varphi _{\omega }\cdot \varphi _{\sigma ^j{\omega }}\circ T_{\omega }^j)$
depends only on
$\mu _{{\omega }}(\varphi _{\omega }\cdot \varphi _{\sigma ^j{\omega }}\circ T_{\omega }^j)$
depends only on
![]() ${\omega }_k$
for
${\omega }_k$
for
![]() $k\leq j$
and that it is bounded by
$k\leq j$
and that it is bounded by
![]() $CK^{-2}({\omega })$
for some constant
$CK^{-2}({\omega })$
for some constant
![]() $C\kern1.2pt{>}\kern1.2pt 0$
(since
$C\kern1.2pt{>}\kern1.2pt 0$
(since
![]() ${\operatorname {\mathrm {esssup}}_{{\omega }\in {\Omega }}(K({\omega })^2\|\varphi _{\omega }\|_{BV}) \kern1.2pt{<}\kern1.2pt\infty }$
). Therefore, the same arguments in the proof of (i) yield that
${\operatorname {\mathrm {esssup}}_{{\omega }\in {\Omega }}(K({\omega })^2\|\varphi _{\omega }\|_{BV}) \kern1.2pt{<}\kern1.2pt\infty }$
). Therefore, the same arguments in the proof of (i) yield that
 $$ \begin{align*} &\int \mu_{{\omega}}(\varphi_{\omega}\cdot (\varphi_{\sigma^j{\omega}}\circ T_{\omega}^j))\mu_{{\sigma}^{i+j}{\omega}}(g_{\sigma^{i+j}{\omega}})\,d{\mathbb P}({\omega})\\&\quad= \int \mu_{{\omega}}(\varphi_{\omega}\cdot (\varphi_{\sigma^j{\omega}}\circ T_{\omega}^j))\,d{\mathbb P}({\omega})\cdot \int \mu_{{\sigma}^{i+j}{\omega}}(g_{\sigma^{i+j}{\omega}})\,d{\mathbb P}({\omega})+J \end{align*} $$
$$ \begin{align*} &\int \mu_{{\omega}}(\varphi_{\omega}\cdot (\varphi_{\sigma^j{\omega}}\circ T_{\omega}^j))\mu_{{\sigma}^{i+j}{\omega}}(g_{\sigma^{i+j}{\omega}})\,d{\mathbb P}({\omega})\\&\quad= \int \mu_{{\omega}}(\varphi_{\omega}\cdot (\varphi_{\sigma^j{\omega}}\circ T_{\omega}^j))\,d{\mathbb P}({\omega})\cdot \int \mu_{{\sigma}^{i+j}{\omega}}(g_{\sigma^{i+j}{\omega}})\,d{\mathbb P}({\omega})+J \end{align*} $$
where
![]() $|J|\leq \gamma _i\|g\|_{L^1}$
and
$|J|\leq \gamma _i\|g\|_{L^1}$
and
![]() $\gamma _i$
is one of the right-hand sides on the upper bounds in (i) (depending on the case) with n replaced by i. Notice next that
$\gamma _i$
is one of the right-hand sides on the upper bounds in (i) (depending on the case) with n replaced by i. Notice next that
(this can be seen by taking
![]() $g=1$
in (4.9)). Hence,
$g=1$
in (4.9)). Hence,
 $$ \begin{align*} \bigg|\!\int({\mathcal K}^i(\varphi {\mathcal K}^j\varphi)-\mu({\mathcal K}^i(\varphi {\mathcal K}^j\varphi))g\,d\mu\bigg|\leq C(e^{-{\unicode{x3bb}} i}+\gamma_i)\|g\|_{L^1} \end{align*} $$
$$ \begin{align*} \bigg|\!\int({\mathcal K}^i(\varphi {\mathcal K}^j\varphi)-\mu({\mathcal K}^i(\varphi {\mathcal K}^j\varphi))g\,d\mu\bigg|\leq C(e^{-{\unicode{x3bb}} i}+\gamma_i)\|g\|_{L^1} \end{align*} $$
and the desired estimate follows again since
![]() $L^\infty $
is the dual of
$L^\infty $
is the dual of
![]() $L^1$
.
$L^1$
.
5 A vector-valued almost sure invariance principle for skew products with uniformly expanding fiber maps and exponentially fast
 ${\alpha }$
-mixing base maps
${\alpha }$
-mixing base maps
Let us first explain why the matrix
![]() $\Sigma ^2$
exists. For a fixed vector v the limit
$\Sigma ^2$
exists. For a fixed vector v the limit
![]() ${s_v^2=\lim _{n\to \infty }(1/n){\mathbb E}[(S_n\cdot v)^2]}$
exists, by considering the real-valued observable
${s_v^2=\lim _{n\to \infty }(1/n){\mathbb E}[(S_n\cdot v)^2]}$
exists, by considering the real-valued observable
![]() $\varphi \cdot v$
. Then the matrix
$\varphi \cdot v$
. Then the matrix
![]() $\Sigma ^2$
from Theorem 2.25 is given by
$\Sigma ^2$
from Theorem 2.25 is given by
![]() $({\Sigma }^2)_{i,j}=\frac {1}2(s_{e_i+e_j}^2-s_{e_i}^2-s_{e_j}^2)$
. This matrix satisfies
$({\Sigma }^2)_{i,j}=\frac {1}2(s_{e_i+e_j}^2-s_{e_i}^2-s_{e_j}^2)$
. This matrix satisfies
![]() $\Sigma ^2 v\cdot v=s_v^2$
and so it is not positive definite if and only if
$\Sigma ^2 v\cdot v=s_v^2$
and so it is not positive definite if and only if
![]() $\varphi \cdot v$
is a coboundary for some unit vector v. Note that this part does not require
$\varphi \cdot v$
is a coboundary for some unit vector v. Note that this part does not require
![]() $T_{\omega }$
to be uniformly expanding.
$T_{\omega }$
to be uniformly expanding.
We assume next that there exist constants
![]() $C>0$
and
$C>0$
and
![]() $\delta \in (0,1)$
such that, for
$\delta \in (0,1)$
such that, for
![]() $\mathbb P$
-a.e.
$\mathbb P$
-a.e.
![]() $\omega $
, we have
$\omega $
, we have
(this is the uniform expansion assumption).
The proof of Theorem 2.25 relies on an application of [Reference Gouëzel24, Theorem 1.2]. The main condition of [Reference Gouëzel24, Theorem 1.2] is the content of the following lemma. Once the lemma is proven Theorem 2.25 follows from [Reference Gouëzel24, Theorem 1.2] applied with an arbitrary large p.
Lemma 5.1. There exist
![]() ${\varepsilon }_0>0$
,
${\varepsilon }_0>0$
,
![]() $c,C>0$
such that for any
$c,C>0$
such that for any
![]() $n,m>0$
,
$n,m>0$
,
![]() $b_1<b_2<\cdots <b_{n+m+1}$
,
$b_1<b_2<\cdots <b_{n+m+1}$
,
![]() $k>0$
and
$k>0$
and
![]() $t_1,\ldots , t_{n+m}\in {\mathbb R}^d$
with
$t_1,\ldots , t_{n+m}\in {\mathbb R}^d$
with
![]() $|t_j|\leq {\varepsilon }_0$
we have
$|t_j|\leq {\varepsilon }_0$
we have
 $$ \begin{align} \Big|\mathbb E_\mu&\big(e^{i\sum_{j=1}^nt_j \cdot (\sum_{\ell=b_j}^{b_{j+1}-1}B_\ell)+i\sum_{j=n+1}^{n+m}t_j \cdot (\sum_{\ell=b_j+k}^{b_{j+1}+k-1}B_\ell)}\big)\nonumber \\ &\quad -\mathbb E_\mu\big(e^{i\sum_{j=1}^nt_j \cdot (\sum_{\ell=b_j}^{b_{j+1}-1}B_\ell)}\big)\cdot\mathbb E_\mu\big(e^{i\sum_{j=n+1}^{n+m}t_j \cdot (\sum_{\ell=b_j+k}^{b_{j+1}+k-1}B_\ell)}\big)\Big|\nonumber \\ &\leq C^{n+m} e^{-ck}, \end{align} $$
$$ \begin{align} \Big|\mathbb E_\mu&\big(e^{i\sum_{j=1}^nt_j \cdot (\sum_{\ell=b_j}^{b_{j+1}-1}B_\ell)+i\sum_{j=n+1}^{n+m}t_j \cdot (\sum_{\ell=b_j+k}^{b_{j+1}+k-1}B_\ell)}\big)\nonumber \\ &\quad -\mathbb E_\mu\big(e^{i\sum_{j=1}^nt_j \cdot (\sum_{\ell=b_j}^{b_{j+1}-1}B_\ell)}\big)\cdot\mathbb E_\mu\big(e^{i\sum_{j=n+1}^{n+m}t_j \cdot (\sum_{\ell=b_j+k}^{b_{j+1}+k-1}B_\ell)}\big)\Big|\nonumber \\ &\leq C^{n+m} e^{-ck}, \end{align} $$
where
![]() $B_\ell =\varphi \circ \tau ^\ell $
.
$B_\ell =\varphi \circ \tau ^\ell $
.
Proof. First, denoting by
![]() ${\mathbb E}_{\omega }$
the expectation with respect to
${\mathbb E}_{\omega }$
the expectation with respect to
![]() $\mu _{\omega }$
, by [Reference Dragičević, Hafouta and Sedro22, Lemma 24] there exist
$\mu _{\omega }$
, by [Reference Dragičević, Hafouta and Sedro22, Lemma 24] there exist
![]() ${\varepsilon }_0>0$
,
${\varepsilon }_0>0$
,
![]() $c,C>0$
with the property that for every
$c,C>0$
with the property that for every
![]() $n,m>0$
,
$n,m>0$
,
![]() $b_1<b_2<\cdots <b_{n+m+1}$
,
$b_1<b_2<\cdots <b_{n+m+1}$
,
![]() $k>0$
and
$k>0$
and
![]() $t_1,\ldots , t_{n+m}\in {\mathbb R}^d$
such that
$t_1,\ldots , t_{n+m}\in {\mathbb R}^d$
such that
![]() $|t_j|\leq {\varepsilon }_0$
,
$|t_j|\leq {\varepsilon }_0$
,
 $$ \begin{align} \Big|\mathbb E_\omega&\big(e^{i\sum_{j=1}^nt_j \cdot (\sum_{\ell=b_j}^{b_{j+1}-1}A_\ell)+i\sum_{j=n+1}^{n+m}t_j \cdot (\sum_{\ell=b_j+k}^{b_{j+1}+k-1}A_\ell)}\big)\nonumber \\ &\quad -\mathbb E_\omega\big(e^{i\sum_{j=1}^nt_j \cdot (\sum_{\ell=b_j}^{b_{j+1}-1}A_\ell)}\big)\cdot\mathbb E_\omega\big(e^{i\sum_{j=n+1}^{n+m}t_j \cdot (\sum_{\ell=b_j+k}^{b_{j+1}+k-1}A_\ell)}\big)\Big|\nonumber \\ &\leq C^{n+m} e^{-ck}, \end{align} $$
$$ \begin{align} \Big|\mathbb E_\omega&\big(e^{i\sum_{j=1}^nt_j \cdot (\sum_{\ell=b_j}^{b_{j+1}-1}A_\ell)+i\sum_{j=n+1}^{n+m}t_j \cdot (\sum_{\ell=b_j+k}^{b_{j+1}+k-1}A_\ell)}\big)\nonumber \\ &\quad -\mathbb E_\omega\big(e^{i\sum_{j=1}^nt_j \cdot (\sum_{\ell=b_j}^{b_{j+1}-1}A_\ell)}\big)\cdot\mathbb E_\omega\big(e^{i\sum_{j=n+1}^{n+m}t_j \cdot (\sum_{\ell=b_j+k}^{b_{j+1}+k-1}A_\ell)}\big)\Big|\nonumber \\ &\leq C^{n+m} e^{-ck}, \end{align} $$
where
![]() $\mathbb E_\omega (g)=\int g h_\omega\, dm$
and
$\mathbb E_\omega (g)=\int g h_\omega\, dm$
and
Let
and
Then with
![]() $B_\ell =\varphi \circ \tau ^\ell $
we have
$B_\ell =\varphi \circ \tau ^\ell $
we have
 $$ \begin{align} \Big|\mathbb E_\mu&\big(e^{i\sum_{j=1}^nt_j \cdot (\sum_{\ell=b_j}^{b_{j+1}-1}B_\ell)+i\sum_{j=n+1}^{n+m}t_j \cdot (\sum_{\ell=b_j+k}^{B_{j+1}+k-1}B_\ell)}\big) \nonumber \\ &\quad -\mathbb E_\mu\big(e^{i\sum_{j=1}^nt_j \cdot (\sum_{\ell=b_j}^{b_{j+1}-1}B_\ell)}\big)\cdot\mathbb E_\mu\big(e^{i\sum_{j=n+1}^{n+m}t_j \cdot (\sum_{\ell=b_j+k}^{b_{j+1}+k-1}B_\ell)}\big)\Big| \nonumber \\ &\leq C^{n+m} e^{-ck}+|\mathrm{Cov}_{\mathbb P}(G,F)|. \end{align} $$
$$ \begin{align} \Big|\mathbb E_\mu&\big(e^{i\sum_{j=1}^nt_j \cdot (\sum_{\ell=b_j}^{b_{j+1}-1}B_\ell)+i\sum_{j=n+1}^{n+m}t_j \cdot (\sum_{\ell=b_j+k}^{B_{j+1}+k-1}B_\ell)}\big) \nonumber \\ &\quad -\mathbb E_\mu\big(e^{i\sum_{j=1}^nt_j \cdot (\sum_{\ell=b_j}^{b_{j+1}-1}B_\ell)}\big)\cdot\mathbb E_\mu\big(e^{i\sum_{j=n+1}^{n+m}t_j \cdot (\sum_{\ell=b_j+k}^{b_{j+1}+k-1}B_\ell)}\big)\Big| \nonumber \\ &\leq C^{n+m} e^{-ck}+|\mathrm{Cov}_{\mathbb P}(G,F)|. \end{align} $$
Using (5.1) and that
![]() $(T_{\omega })_*\mu _{\omega }=\mu _{{\sigma }{\omega }}$
, we get that there are
$(T_{\omega })_*\mu _{\omega }=\mu _{{\sigma }{\omega }}$
, we get that there are
![]() $k_0\in \mathbb Z $
and functions
$k_0\in \mathbb Z $
and functions
![]() $G_1$
and
$G_1$
and
![]() $F_1$
such that
$F_1$
such that
and
Thus,
where we have used that
![]() $G_1,G_2,G$
and F are uniformly bounded (so the above constants
$G_1,G_2,G$
and F are uniformly bounded (so the above constants
![]() $C',C"$
do not depend on the choice of
$C',C"$
do not depend on the choice of
![]() $b_j,t_j$
, etc.). On the other hand, by (3.7),
$b_j,t_j$
, etc.). On the other hand, by (3.7),
Thus,
 $$ \begin{align} \Big|\mathbb E_\mu&\big(e^{i\sum_{j=1}^nt_j \cdot (\sum_{\ell=b_j}^{b_{j+1}-1}B_\ell)+i\sum_{j=n+1}^{n+m}t_j \cdot (\sum_{\ell=b_j+k}^{B_{j+1}+k-1}B_\ell)}\big) \nonumber \\ &\quad -\mathbb E_\mu\big(e^{i\sum_{j=1}^nt_j \cdot (\sum_{\ell=b_j}^{b_{j+1}-1}B_\ell)}\big)\cdot\mathbb E_\mu\big(e^{i\sum_{j=n+1}^{n+m}t_j \cdot (\sum_{\ell=b_j+k}^{b_{j+1}+k-1}B_\ell)}\big)\Big| \nonumber \\ &\leq C^{n+m} e^{-ck}+C"\delta^{\delta k/4}+C"'\alpha^{k/2}. \end{align} $$
$$ \begin{align} \Big|\mathbb E_\mu&\big(e^{i\sum_{j=1}^nt_j \cdot (\sum_{\ell=b_j}^{b_{j+1}-1}B_\ell)+i\sum_{j=n+1}^{n+m}t_j \cdot (\sum_{\ell=b_j+k}^{B_{j+1}+k-1}B_\ell)}\big) \nonumber \\ &\quad -\mathbb E_\mu\big(e^{i\sum_{j=1}^nt_j \cdot (\sum_{\ell=b_j}^{b_{j+1}-1}B_\ell)}\big)\cdot\mathbb E_\mu\big(e^{i\sum_{j=n+1}^{n+m}t_j \cdot (\sum_{\ell=b_j+k}^{b_{j+1}+k-1}B_\ell)}\big)\Big| \nonumber \\ &\leq C^{n+m} e^{-ck}+C"\delta^{\delta k/4}+C"'\alpha^{k/2}. \end{align} $$
6 Extensions, generalizations, additional results and a short discussion
In this section we will describe a few additional results which can also be obtained using the methods of the current paper. In order not to overload the paper the section is presented in a form of a discussion rather than explicit formulations of theorems.
6.1 More general mixing base maps for continuous in
 ${\omega }$
transfer operators
${\omega }$
transfer operators
Let
![]() $(\xi _n)_{n\in \mathbb Z}$
be a stationary process taking values on a metric space
$(\xi _n)_{n\in \mathbb Z}$
be a stationary process taking values on a metric space
![]() $(\mathcal Y,d)$
satisfying the following approximation and mixing conditions.
$(\mathcal Y,d)$
satisfying the following approximation and mixing conditions.
There are sub-
![]() $\sigma $
-algebras
$\sigma $
-algebras
![]() ${\mathcal G}_{n,m}$
on the underlying probability space such that
${\mathcal G}_{n,m}$
on the underlying probability space such that
![]() ${\mathcal G}_{n,m}\subset {\mathcal G}_{n_1,m_1}$
if
${\mathcal G}_{n,m}\subset {\mathcal G}_{n_1,m_1}$
if
![]() $[n,m]\subset [n_1,m_1]$
and for each r and n there is an
$[n,m]\subset [n_1,m_1]$
and for each r and n there is an
![]() ${\mathcal G}_{n-r,n+r}$
measurable random variable
${\mathcal G}_{n-r,n+r}$
measurable random variable
![]() $\xi _{n,r}$
so that the following assertions hold.
$\xi _{n,r}$
so that the following assertions hold.
(1) Approximation.
![]() $\|d(\xi _n,\xi _{n,r})\|_{L^\infty }\leq A_1\beta ^r$
,
$\|d(\xi _n,\xi _{n,r})\|_{L^\infty }\leq A_1\beta ^r$
,
![]() $\beta \in (0,1)$
.
$\beta \in (0,1)$
.
(2) Mixing. The sequences
![]() $(\xi _{2nr,r})_{n\in \mathbb Z}$
are
$(\xi _{2nr,r})_{n\in \mathbb Z}$
are
![]() $\alpha $
-mixing (or
$\alpha $
-mixing (or
![]() $\phi _R$
- or
$\phi _R$
- or
![]() $\psi $
-mixing) uniformly in r.
$\psi $
-mixing) uniformly in r.
We note that the above uniform approximation by
![]() ${\alpha }$
-mixing sequences applies to the case where
${\alpha }$
-mixing sequences applies to the case where
![]() $\xi _j$
has the form
$\xi _j$
has the form
![]() $\xi _j=S^j\xi _0$
, in which S is an invertible Young tower. In this case we take
$\xi _j=S^j\xi _0$
, in which S is an invertible Young tower. In this case we take
 $$ \begin{align*} {\mathcal G}_{n,m}=\bigwedge_{j=n}^{m}S^{-j}{\mathcal A}, \end{align*} $$
$$ \begin{align*} {\mathcal G}_{n,m}=\bigwedge_{j=n}^{m}S^{-j}{\mathcal A}, \end{align*} $$
where
![]() ${\mathcal A}$
is the partition that defines the tower. Then
${\mathcal A}$
is the partition that defines the tower. Then
![]() ${\alpha }_n=O(n^{-(p-2)})$
if the tails of the tower are
${\alpha }_n=O(n^{-(p-2)})$
if the tails of the tower are
![]() $O(n^{-p})$
for some
$O(n^{-p})$
for some
![]() $p\geq 3$
. We can also consider several classes of smooth maps S on the interval or Gibbs–Markov maps [Reference Aaronson and Denker1] for which such an approximation holds with
$p\geq 3$
. We can also consider several classes of smooth maps S on the interval or Gibbs–Markov maps [Reference Aaronson and Denker1] for which such an approximation holds with
![]() $\psi _n=O({\delta }^n)$
for some
$\psi _n=O({\delta }^n)$
for some
![]() ${\delta }\in (0,1)$
.
${\delta }\in (0,1)$
.
Let
![]() $(\Omega ,\mathcal F,\mathbb P,\sigma )$
be the shift system constructed as before. Then all the results stated in the paper hold true when
$(\Omega ,\mathcal F,\mathbb P,\sigma )$
be the shift system constructed as before. Then all the results stated in the paper hold true when
![]() $\omega \to \mathcal L_{\omega }$
and
$\omega \to \mathcal L_{\omega }$
and
![]() $\omega \to \varphi _\omega $
are Hölder continuous in
$\omega \to \varphi _\omega $
are Hölder continuous in
![]() $\omega $
(on a set with probability
$\omega $
(on a set with probability
![]() $1$
). The main point is that Lemma 3.8 and the similar approximations used in the construction of the martingale (that is, in the proof of Proposition 4.3) can be obtained by first approximating (taking
$1$
). The main point is that Lemma 3.8 and the similar approximations used in the construction of the martingale (that is, in the proof of Proposition 4.3) can be obtained by first approximating (taking
![]() $r=r_n={\varepsilon }_0n$
for some small
$r=r_n={\varepsilon }_0n$
for some small
![]() ${\varepsilon }_0$
) and using the mixing conditions on the approximating sequences. The main reason we did not include such results in the body of the paper is that it would make the notation more complicated, and that the additional essentially global regularity assumptions on the transfer operators are somehow less natural.
${\varepsilon }_0$
) and using the mixing conditions on the approximating sequences. The main reason we did not include such results in the body of the paper is that it would make the notation more complicated, and that the additional essentially global regularity assumptions on the transfer operators are somehow less natural.
6.2 Extension to random Gibbs measures
Let us now consider the random expanding maps
![]() $T_{\omega }$
as in [Reference Mayer, Skorulski and Urbański44]. Let
$T_{\omega }$
as in [Reference Mayer, Skorulski and Urbański44]. Let
![]() $\mu _{\omega }=h_{\omega } \nu _{\omega }$
be a random Gibbs measure corresponding to a given random logarithmically
$\mu _{\omega }=h_{\omega } \nu _{\omega }$
be a random Gibbs measure corresponding to a given random logarithmically
![]() ${\alpha }$
-Hölder continuous potential, and let
${\alpha }$
-Hölder continuous potential, and let
![]() ${\unicode{x3bb} }_{\omega }$
be the exponent of the random pressure. Namely, if
${\unicode{x3bb} }_{\omega }$
be the exponent of the random pressure. Namely, if
![]() ${\mathcal L}_{\omega }$
is the transfer operator corresponding to the random potential, then
${\mathcal L}_{\omega }$
is the transfer operator corresponding to the random potential, then
Next, for the sake of simplicity let us consider here random expanding maps as in [Reference Hafouta and Kifer31, Ch. 5]. Then there is a constant
![]() $K>0$
such that with
$K>0$
such that with
![]() $\tilde {\mathcal L}_{\omega }={\mathcal L}_{\omega }/{\unicode{x3bb} }_{\omega }$
we have
$\tilde {\mathcal L}_{\omega }={\mathcal L}_{\omega }/{\unicode{x3bb} }_{\omega }$
we have
where
![]() $\|\cdot \|_{\mathrm {Holder}}$
is the usual Hölder norm corresponding to the exponent
$\|\cdot \|_{\mathrm {Holder}}$
is the usual Hölder norm corresponding to the exponent
![]() ${\alpha }$
and
${\alpha }$
and
![]() ${\nu \otimes h(g)=\nu (g)h}$
. Plugging in
${\nu \otimes h(g)=\nu (g)h}$
. Plugging in
![]() $g=\textbf {1}$
we get similar estimates to those we had in (2.10):
$g=\textbf {1}$
we get similar estimates to those we had in (2.10):
Remark also that
![]() $h_{\omega }\geq c>0$
for some constant
$h_{\omega }\geq c>0$
for some constant
![]() $c>0$
(see [Reference Hafouta and Kifer31]).
$c>0$
(see [Reference Hafouta and Kifer31]).
The main additional difficulty here is to estimate expressions of the form
![]() $\mu _{\omega }(F_{\omega })$
(as in Lemma 3.8) by functions of the coordinates in places j for
$\mu _{\omega }(F_{\omega })$
(as in Lemma 3.8) by functions of the coordinates in places j for
![]() $|j|\leq n$
. Once this is achieved, we can use the approximation argument (similarly to Lemma 3.8) which was essential in the proofs of all of the results stated in the body of the paper. The main difference in comparison to the case where
$|j|\leq n$
. Once this is achieved, we can use the approximation argument (similarly to Lemma 3.8) which was essential in the proofs of all of the results stated in the body of the paper. The main difference in comparison to the case where
![]() $\nu _{\omega }=m$
does not depend on
$\nu _{\omega }=m$
does not depend on
![]() ${\omega }$
is that now we need to approximate
${\omega }$
is that now we need to approximate
![]() $\nu _{\omega }$
by functions of the first n coordinates (exponentially fast in n). For uniformly expanding maps, this follows from the construction of
$\nu _{\omega }$
by functions of the first n coordinates (exponentially fast in n). For uniformly expanding maps, this follows from the construction of
![]() $\nu _{\omega }$
as a certain uniform limit (see [Reference Hafouta and Kifer31, Chs. 4–5]).
$\nu _{\omega }$
as a certain uniform limit (see [Reference Hafouta and Kifer31, Chs. 4–5]).
6.3 Extension to non-conventional sums (multiple recurrences)
Let us consider partial ‘non-conventional’ sums of the form
 $$ \begin{align*} S_n\varphi=\sum_{m=1}^{n}\prod_{j=1}^\ell \varphi\circ\tau^{q_j(m)}, \end{align*} $$
$$ \begin{align*} S_n\varphi=\sum_{m=1}^{n}\prod_{j=1}^\ell \varphi\circ\tau^{q_j(m)}, \end{align*} $$
where
![]() $\ell $
is an integer and
$\ell $
is an integer and
![]() $q_j(n)$
are positive integer-valued sequences. The statistical properties of such sums have been studied for several classes of expanding or hyperbolic maps (in particular); see [Reference Hafouta25, Reference Kifer39, Reference Kifer and Varadhan41] and references therein. When all the
$q_j(n)$
are positive integer-valued sequences. The statistical properties of such sums have been studied for several classes of expanding or hyperbolic maps (in particular); see [Reference Hafouta25, Reference Kifer39, Reference Kifer and Varadhan41] and references therein. When all the
![]() $q_j$
are polynomials, we believe that all the results obtained using the method of cumulants (that is, Theorems 2.14–2.17 and an appropriate version of Theorem 2.19) can be obtained for such sums exactly as in [Reference Hafouta25], relying on a version of Proposition 3.4 applied with
$q_j$
are polynomials, we believe that all the results obtained using the method of cumulants (that is, Theorems 2.14–2.17 and an appropriate version of Theorem 2.19) can be obtained for such sums exactly as in [Reference Hafouta25], relying on a version of Proposition 3.4 applied with
![]() $\rho (n,m)=\max _{1\leq i,j\leq \ell }|q_i(m)-q_j(n)|$
. The main idea is that by induction on the number of blocks we can show that the conditions of Proposition 3.3 with
$\rho (n,m)=\max _{1\leq i,j\leq \ell }|q_i(m)-q_j(n)|$
. The main idea is that by induction on the number of blocks we can show that the conditions of Proposition 3.3 with
![]() $\rho =\rho _\ell $
hold true for
$\rho =\rho _\ell $
hold true for
 $$ \begin{align*}X_m=\prod_{j=1}^\ell \varphi\circ\tau^{q_j(m)}.\end{align*} $$
$$ \begin{align*}X_m=\prod_{j=1}^\ell \varphi\circ\tau^{q_j(m)}.\end{align*} $$
That is, by an inductive argument similar to that in [Reference Hafouta and Kifer31, Corollary 1.3.11], we can prove the following result.
Lemma 6.1. Let
![]() $r\in {\mathbb N}$
and let
$r\in {\mathbb N}$
and let
![]() $B_1,B_2,\ldots , B_k$
be finite subsets of
$B_1,B_2,\ldots , B_k$
be finite subsets of
![]() ${\mathbb N}$
so that the distance between
${\mathbb N}$
so that the distance between
![]() $B_j$
and
$B_j$
and
![]() $B_{j+1}$
is
$B_{j+1}$
is
![]() $d_j$
. Set
$d_j$
. Set
![]() $r_j=[d_j/3]$
. Let
$r_j=[d_j/3]$
. Let
![]() ${\mathcal C}=\{{\mathcal C}_j:\,1\leq j\leq s\}$
be a partition of
${\mathcal C}=\{{\mathcal C}_j:\,1\leq j\leq s\}$
be a partition of
![]() $\{1,2,\ldots , k\}$
and set
$\{1,2,\ldots , k\}$
and set
![]() $Y_j=\prod _{k\in {\mathcal C}_j}\prod _{u\in B_k}\varphi \circ \tau ^{u}$
. Then, assuming that
$Y_j=\prod _{k\in {\mathcal C}_j}\prod _{u\in B_k}\varphi \circ \tau ^{u}$
. Then, assuming that
![]() $\|\varphi \|_{L^\infty }\leq 1$
and that
$\|\varphi \|_{L^\infty }\leq 1$
and that
![]() $\operatorname {\mathrm {esssup}}_{{\omega }\in {\Omega }}(K({\omega })\|\varphi _{\omega }\|_{BV})\leq 1$
, there is an absolute constant
$\operatorname {\mathrm {esssup}}_{{\omega }\in {\Omega }}(K({\omega })\|\varphi _{\omega }\|_{BV})\leq 1$
, there is an absolute constant
![]() $A>1$
such that
$A>1$
such that
 $$ \begin{align*} \bigg|{\mathbb E}_\mu\bigg[\prod_{j=1}^s Y_j\bigg]-\prod_{j=1}^s{\mathbb E}_\mu[Y_j]\bigg|\leq A^m\sum_{j=1}^{m}(\delta^{r_j}+\alpha([r_j])) \end{align*} $$
$$ \begin{align*} \bigg|{\mathbb E}_\mu\bigg[\prod_{j=1}^s Y_j\bigg]-\prod_{j=1}^s{\mathbb E}_\mu[Y_j]\bigg|\leq A^m\sum_{j=1}^{m}(\delta^{r_j}+\alpha([r_j])) \end{align*} $$
where
![]() ${\delta }=e^{-({\unicode{x3bb} }-3{\varepsilon })/2}\in (0,1)$
.
${\delta }=e^{-({\unicode{x3bb} }-3{\varepsilon })/2}\in (0,1)$
.
We note that in order to prove a version of the functional CLT for the sums above we first need to use the arguments in [Reference Hafouta and Kifer30, Reference Kifer and Varadhan41] to compute the variance of the limiting Gaussian, which for general polynomials might differ from a Brownian motion, and this can also be done by using the above lemma.