Hostname: page-component-7479d7b7d-pfhbr Total loading time: 0 Render date: 2024-07-11T01:45:19.668Z Has data issue: false hasContentIssue false
  • English
  • Français

Is a typical bi-Perron algebraic unit a pseudo-Anosov dilatation?

Published online by Cambridge University Press:  28 November 2017

HYUNGRYUL BAIK ,
AHMAD RAFIQI  and
CHENXI WU
HYUNGRYUL BAIK
Affiliation:
Department of Mathematical Sciences, KAIST, 291 Daehak-ro, Daejeon, South Korea email hrbaik@kaist.ac.kr
AHMAD RAFIQI
Affiliation:
Department of Mathematics, Cornell University, Malott Hall, Ithaca, NY 14853, USA email ar776@cornell.edu
CHENXI WU
Affiliation:
Department of Mathematics, Rutgers University, Hill Center – Busch Campus, 110 Frelinghuysen Road, Piscataway, NJ 08854-8019, USA email wchenxi2013@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

In this note, we deduce a partial answer to the question in the title. In particular, we show that asymptotically almost all bi-Perron algebraic units whose characteristic polynomial has degree at most 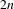$2n$ do not correspond to dilatations of pseudo-Anosov maps on a closed orientable surface of genus $n$ for 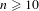$n\geq 10$. As an application of the argument, we also obtain a statement on the number of closed geodesics of the same length in the moduli space of area-one abelian differentials for low-genus cases.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 7 , July 2019 , pp. 1745 - 1750
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arnoux, P. and Yoccoz, J.. Construction de difféomorphisms pseudo-Anosov. C. R. Acad. Sci. Paris 292 (1980), 75–78.Google Scholar
Baik, H., Rafiqi, A. and Wu, C.. Constructing pseudo-Anosov maps with given dilatations. Geom. Dedicata 180(1) (2016), 39–48.Google Scholar
Beardon, A. F.. Complex Analysis: The Argument Principle in Analysis and Topology. Wiley-Interscience, John Wiley, Chichester, 1979.Google Scholar
de Carvalho, A. and Hall, T.. Unimodal generalized pseudo-Anosov maps. Geom. Topol. 8 (2004), 1127–1188.Google Scholar
Eskin, A. and Mirzakhani, M.. Counting closed geodesics in moduli space. J. Mod. Dyn. 5 (2011), 71–105.Google Scholar
Eskin, A., Mirzakhani, M. and Rafi, K.. Counting closed geodesics in strata. Preprint 2012, arXiv:1206.5574.Google Scholar
Farb, B. and Margalit, D.. A Primer on Mapping Class Groups (Princeton Mathematical Series, 49) . Princeton University Press, Princeton, NJ, 2012.Google Scholar
Fried, D.. Growth rate of surface homeomorphisms and flow equivalence. Ergod. Th. & Dynam. Sys. 5(04) (1985), 539–563.Google Scholar
Funkhouser, H. G.. A short account of the history of symmetric functions of roots of equations. Amer. Math. Monthly 37(7) (1930), 357–365.Google Scholar
Hamenstädt, U.. Symbolic dynamics for the Teichmüller flow. Preprint 2011, arXiv:1112.6107.Google Scholar
Hamenstädt, U.. Bowen’s construction for the Teichmüller flow. J. Mod. Dyn. 7 (2013), 489–526.Google Scholar
Hamenstädt, U.. Typical properties of periodic Teichmüller geodesics. Preprint 2014, arXiv:1409.5978.Google Scholar
Hironaka, E.. Small dilatation mapping classes coming from the simplest hyperbolic braid. Algebr. Geom. Topol. 10(4) (2010), 2041–2060.Google Scholar
Lanneau, E. and Thiffeault, J.. On the minimum dilatation of braids on punctured discs. Geom. Dedicata 152 (2011), 165–182.Google Scholar
Lanneau, E. and Thiffeault, J.. On the minimum dilatation of pseudoAnosov homeromorphisms on surfaces of small genus. Ann. Inst. Fourier (Grenoble) 61(1) (2011), 105–144.Google Scholar
Leininger, C.. On groups generated by two positive multi-twists: Teichmuller curves and Lehmer’s number. Geom. Topol. 8 (2004), 1301–1359.Google Scholar
Long, D.. Constructing pseudo-Anosov maps. Knot Theory and Manifolds (Vancouver, BC, 1983) (Lecture Notes in Mathematics, 1144) . Springer, Berlin, 1985, pp. 108–114.Google Scholar
Masur, H.. Interval exchange transformations and measured foliations. Ann. of Math. 115 (1982), 169–201.Google Scholar
Penner, R.. A construction of pseudo-Anosov homeomorphisms. Trans. Amer. Math. Soc. 310(1) (1988), 179–197.Google Scholar
Shin, H. and Strenner, B.. Pseudo-Anosov mapping classes not arising from Penner’s construction. Geom. Topol. 19 (2015), 3645–3656.Google Scholar
Thurston, W.. On the geometry and dynamics of diffeomorphisms of surfaces. Bull. Amer. Math. Soc. (N.S.) 19 (1988), 417–431.Google Scholar
Thurston, W.. Entropy in dimension one. Preprint, 2014, arXiv:1402.2008.Google Scholar
A. Faithi, F. Laudenbach and V. Poenaru (eds). Travaux de Thurston sur les surfaces (Astérisque, 66–67). Société Mathématique de France, Paris, 1979. Séminaire Orsay, With an English summary.Google Scholar
Veech, W.. The Teichmüller geodesic flow. Ann. Math. 124 (1986), 441–530.Google Scholar