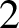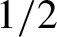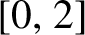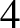1. Introduction and main results
In this paper we study the dynamics of transcendental meromorphic functions. It is well known that many dynamical behaviours of the function depend, to certain extent, on the iterative behaviours of its singular values. By definition,
![]() $a\in \operatorname {\widehat {\mathbb C}}$
is a singular value of a meromorphic function f if it is either a critical or asymptotic value of f.
$a\in \operatorname {\widehat {\mathbb C}}$
is a singular value of a meromorphic function f if it is either a critical or asymptotic value of f.
Much recent attention in transcendental dynamics is directed to the so-called Speiser class
![]() $\operatorname {\mathcal {S}}$
, consisting of meromorphic functions with a finite number of singular values; see, for instance, [Reference BishopBis15, Reference BishopBis17, Reference Eremenko and LyubichEL92, Reference Goldberg and KeenGK86]. These functions are called Speiser functions. Many familiar functions belong to this class, including, for example, the exponential family, the cosine family and the tangent family. Speiser functions are studied in great detail and provide dynamical behaviours similar to those of polynomial and rational maps.
$\operatorname {\mathcal {S}}$
, consisting of meromorphic functions with a finite number of singular values; see, for instance, [Reference BishopBis15, Reference BishopBis17, Reference Eremenko and LyubichEL92, Reference Goldberg and KeenGK86]. These functions are called Speiser functions. Many familiar functions belong to this class, including, for example, the exponential family, the cosine family and the tangent family. Speiser functions are studied in great detail and provide dynamical behaviours similar to those of polynomial and rational maps.
We intend to study functions in the Speiser class with only few singular values. Even with this restriction, the classes of functions are quite diverse; see discussion in the next section. One can thus reasonably expect that very rich and diverse dynamical behaviours could occur in this case. Our main result will confirm this in a strong sense. Recall that for a meromorphic function f, the escaping set
![]() $\operatorname {\mathcal {I}}(f)$
of f is the set of points which tend to
$\operatorname {\mathcal {I}}(f)$
of f is the set of points which tend to
![]() $\infty $
under iteration. This set plays a fundamental role in recent studies of transcendental dynamics. Starting with McMullen [Reference McMullenMcM87], a wide range of research focuses on estimating the Hausdorff dimensions of escaping sets; see, for instance, [Reference BarańskiBar08, Reference Bergweiler, Karpińska and StallardBKS09, Reference Rempe and StallardRS10, Reference SchubertSch07] for some entire functions and [Reference Bergweiler and KotusBK12, Reference CuiCui21b, Reference Galazka and KotusGK18] for certain meromorphic functions. Some of these papers also treat special Speiser functions. A natural question arises: what are the possible values of the Hausdorff dimensions of escaping sets for Speiser functions? This was resolved recently by the present authors in [Reference Aspenberg and CuiAC21]: any number in
$\infty $
under iteration. This set plays a fundamental role in recent studies of transcendental dynamics. Starting with McMullen [Reference McMullenMcM87], a wide range of research focuses on estimating the Hausdorff dimensions of escaping sets; see, for instance, [Reference BarańskiBar08, Reference Bergweiler, Karpińska and StallardBKS09, Reference Rempe and StallardRS10, Reference SchubertSch07] for some entire functions and [Reference Bergweiler and KotusBK12, Reference CuiCui21b, Reference Galazka and KotusGK18] for certain meromorphic functions. Some of these papers also treat special Speiser functions. A natural question arises: what are the possible values of the Hausdorff dimensions of escaping sets for Speiser functions? This was resolved recently by the present authors in [Reference Aspenberg and CuiAC21]: any number in
![]() $[0,2]$
can be achieved. In a larger setting (that is, those meromorphic functions with a bounded set of finite singular values), Bergweiler and Kotus proved a similar result [Reference Bergweiler and KotusBK12].
$[0,2]$
can be achieved. In a larger setting (that is, those meromorphic functions with a bounded set of finite singular values), Bergweiler and Kotus proved a similar result [Reference Bergweiler and KotusBK12].
This paper is a natural continuation of [Reference Aspenberg and CuiAC21] and focuses on exploring a relation between the number of singular values and possible attainable Hausdorff dimensions for escaping sets. For convenience, we will use
![]() $\operatorname {\mathcal {S}}_{q}$
to denote Speiser functions with exactly q singular values on
$\operatorname {\mathcal {S}}_{q}$
to denote Speiser functions with exactly q singular values on
![]() $\operatorname {\widehat {\mathbb C}}$
.
$\operatorname {\widehat {\mathbb C}}$
.
Our starting point is the following theorem, which brings together results of several authors; see [Reference Galazka and KotusGK18, Reference McMullenMcM87] (and also [Reference CuiCui21b, Theorem 1]). By
![]() $\operatorname {dim} E$
we mean the Hausdorff dimension of the set E.
$\operatorname {dim} E$
we mean the Hausdorff dimension of the set E.
Theorem A.
Meromorphic functions in
![]() $\operatorname {\mathcal {S}}_{2}$
have explicit formulas; see Theorem 2.1 in the next section for a simple proof. As the number of singular values increases, the varieties of functions are also increasing. Thus one can reasonably expect that a more flexible result would hold. This is indeed the case, as shown by the following result.
$\operatorname {\mathcal {S}}_{2}$
have explicit formulas; see Theorem 2.1 in the next section for a simple proof. As the number of singular values increases, the varieties of functions are also increasing. Thus one can reasonably expect that a more flexible result would hold. This is indeed the case, as shown by the following result.
Theorem 1.1.
The existing gap between Theorem A and Theorem 1.1 is the class
![]() $\operatorname {\mathcal {S}}_{3}$
. It is plausible that the above theorem holds in
$\operatorname {\mathcal {S}}_{3}$
. It is plausible that the above theorem holds in
![]() $\operatorname {\mathcal {S}}_{3}$
. However, our construction will not give this.
$\operatorname {\mathcal {S}}_{3}$
. However, our construction will not give this.
Another point that we would like to address concerns a question for the invariance of Hausdorff dimensions of escaping sets. To be more specific, it asks whether two quasiconformally equivalent functions will have escaping sets of equal Hausdorff dimension. We say that two Speiser functions f and g are quasiconformally equivalent if there are quasiconformal mappings
![]() $\varphi ,\psi :\operatorname {\mathbb C}\to \operatorname {\mathbb C}$
such that
$\varphi ,\psi :\operatorname {\mathbb C}\to \operatorname {\mathbb C}$
such that
![]() $\varphi \circ f=g\circ \psi $
; see [Reference Eremenko and LyubichEL92]. (We can also define topological equivalence by requiring
$\varphi \circ f=g\circ \psi $
; see [Reference Eremenko and LyubichEL92]. (We can also define topological equivalence by requiring
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
to be homeomorphisms.) The above question was originally asked for entire functions which are not necessarily Speiser functions. Counterexamples were recently given in the meromorphic setting in [Reference Aspenberg and CuiAC21]. Here we provide another class of counterexamples.
$\psi $
to be homeomorphisms.) The above question was originally asked for entire functions which are not necessarily Speiser functions. Counterexamples were recently given in the meromorphic setting in [Reference Aspenberg and CuiAC21]. Here we provide another class of counterexamples.
Theorem 1.2. There exist quasiconformally equivalent meromorphic functions
![]() ${f,g\in \operatorname {\mathcal {S}}_{4}}$
for which
${f,g\in \operatorname {\mathcal {S}}_{4}}$
for which
![]() $\operatorname {dim}\operatorname {\mathcal {I}}(f)\neq \operatorname {dim}\operatorname {\mathcal {I}}(g)$
.
$\operatorname {dim}\operatorname {\mathcal {I}}(f)\neq \operatorname {dim}\operatorname {\mathcal {I}}(g)$
.
We also remark that if two quasiconformally equivalent meromorphic functions belong to
![]() $\operatorname {\mathcal {S}}_{3}$
, then they are actually conformally equivalent (see [Reference Bergweiler and CuiBC21, Lemma 2.3]). This implies immediately that two such functions have the same order of growth. It is plausible that two such functions will have escaping sets of the same Hausdorff dimension. In this sense, the above Theorem 1.2 may be optimal.
$\operatorname {\mathcal {S}}_{3}$
, then they are actually conformally equivalent (see [Reference Bergweiler and CuiBC21, Lemma 2.3]). This implies immediately that two such functions have the same order of growth. It is plausible that two such functions will have escaping sets of the same Hausdorff dimension. In this sense, the above Theorem 1.2 may be optimal.
1.1. Structure of the paper
In §2 we briefly discuss transcendental meromorphic functions with few singular values. In §3 we construct meromorphic functions with four singular values of arbitrary order. Finally, in §4 we present an outline of the estimate for the Hausdorff dimension of their escaping sets.
2. Speiser functions with few singular values
Let
 $f:\operatorname {\mathbb C}\to \operatorname {\widehat {\mathbb C}}$
be transcendental and meromorphic. We say that c is a critical value of f if c has a preimage with zero spherical derivative. With this definition,
$f:\operatorname {\mathbb C}\to \operatorname {\widehat {\mathbb C}}$
be transcendental and meromorphic. We say that c is a critical value of f if c has a preimage with zero spherical derivative. With this definition,
![]() $\infty $
will be a critical value if there are any multiple poles.
$\infty $
will be a critical value if there are any multiple poles.
![]() $a\in \operatorname {\widehat {\mathbb C}}$
is an asymptotic value of f if there exists a curve
$a\in \operatorname {\widehat {\mathbb C}}$
is an asymptotic value of f if there exists a curve
![]() $\gamma $
tending to
$\gamma $
tending to
![]() $\infty $
such that
$\infty $
such that
![]() $f(\gamma )$
tends to a. As a simple example,
$f(\gamma )$
tends to a. As a simple example,
![]() $0$
and
$0$
and
![]() $\infty $
are asymptotic values of
$\infty $
are asymptotic values of
![]() $e^{z}$
. A value s is called a singular value if it is either a critical or asymptotic value. See [Reference Bergweiler and EremenkoBE95] for a classification of singularities of the inverse of a meromorphic function. Singular values play a vital role in the dynamics of meromorphic functions; we refer to [Reference BergweilerBer93] for more details and explanations.
$e^{z}$
. A value s is called a singular value if it is either a critical or asymptotic value. See [Reference Bergweiler and EremenkoBE95] for a classification of singularities of the inverse of a meromorphic function. Singular values play a vital role in the dynamics of meromorphic functions; we refer to [Reference BergweilerBer93] for more details and explanations.
Meromorphic functions with two singular values. The following simple fact concerning meromorphic functions with two singular values is folklore and it is not easy to locate a reference. Therefore, the outline of a proof is presented for completeness. Recall that
![]() $\operatorname {\mathcal {S}}_{q}$
denotes the class of Speiser functions with exactly q singular values.
$\operatorname {\mathcal {S}}_{q}$
denotes the class of Speiser functions with exactly q singular values.
Theorem 2.1. Let
![]() $f\in \operatorname {\mathcal {S}}_{2}$
. Then f is of the form
$f\in \operatorname {\mathcal {S}}_{2}$
. Then f is of the form
![]() $M\circ \exp \circ A$
, where M is Möbius and A is linear.
$M\circ \exp \circ A$
, where M is Möbius and A is linear.
Proof Sketch of proof
Without loss of generality, we assume that the two singular values of f are
![]() $0$
and
$0$
and
![]() $\infty $
. Otherwise we consider
$\infty $
. Otherwise we consider
![]() $M_{1}\circ f$
, where
$M_{1}\circ f$
, where
![]() $M_{1}$
is a Möbius transformation sending the two singular values of f to
$M_{1}$
is a Möbius transformation sending the two singular values of f to
![]() $0$
and
$0$
and
![]() $\infty $
. Then
$\infty $
. Then
 $$ \begin{align*}f:\operatorname{\mathbb C}\setminus\{f^{-1}(0),\,f^{-1}(\infty)\}\rightarrow \operatorname{\widehat{\mathbb C}}\setminus\{0,\infty\}\end{align*} $$
$$ \begin{align*}f:\operatorname{\mathbb C}\setminus\{f^{-1}(0),\,f^{-1}(\infty)\}\rightarrow \operatorname{\widehat{\mathbb C}}\setminus\{0,\infty\}\end{align*} $$
is a covering map. Note that the fundamental group of
 $\operatorname {\widehat {\mathbb C}}\setminus \{0,\infty \}$
is isomorphic to
$\operatorname {\widehat {\mathbb C}}\setminus \{0,\infty \}$
is isomorphic to
![]() $\mathbb {Z}$
. The transcendence of f then implies that the fundamental group of
$\mathbb {Z}$
. The transcendence of f then implies that the fundamental group of
![]() $\operatorname {\mathbb C}\setminus \{f^{-1}(0),\,f^{-1}(\infty )\}$
is trivial and thus
$\operatorname {\mathbb C}\setminus \{f^{-1}(0),\,f^{-1}(\infty )\}$
is trivial and thus
![]() $\operatorname {\mathbb C}\setminus \{f^{-1}(0),\,f^{-1}(\infty )\}$
is simply connected such that the above f is a universal covering to
$\operatorname {\mathbb C}\setminus \{f^{-1}(0),\,f^{-1}(\infty )\}$
is simply connected such that the above f is a universal covering to
 $\operatorname {\widehat {\mathbb C}}\setminus \{0,\infty \}$
. Since meromorphic functions are discrete maps, we have that
$\operatorname {\widehat {\mathbb C}}\setminus \{0,\infty \}$
. Since meromorphic functions are discrete maps, we have that
![]() $\operatorname {\mathbb C}\setminus \{f^{-1}(0),\,f^{-1}(\infty )\}=\operatorname {\mathbb C}$
. This implies that both singular values are actually omitted. Note that the exponential map
$\operatorname {\mathbb C}\setminus \{f^{-1}(0),\,f^{-1}(\infty )\}=\operatorname {\mathbb C}$
. This implies that both singular values are actually omitted. Note that the exponential map
![]() $\exp $
is a holomorphic universal covering from
$\exp $
is a holomorphic universal covering from
![]() $\operatorname {\mathbb C}$
to
$\operatorname {\mathbb C}$
to
 $ \operatorname {\widehat {\mathbb C}}\setminus \{0,\infty \}$
. Now it follows from the essential uniqueness of the universal covering spaces that there exists a holomorphic homeomorphism
$ \operatorname {\widehat {\mathbb C}}\setminus \{0,\infty \}$
. Now it follows from the essential uniqueness of the universal covering spaces that there exists a holomorphic homeomorphism
![]() $\phi : \operatorname {\mathbb C}\to \operatorname {\mathbb C}$
such that
$\phi : \operatorname {\mathbb C}\to \operatorname {\mathbb C}$
such that
![]() $f=\exp \circ \phi $
. Since a holomorphic homeomorphism of the complex plane must be a linear map, we thus have
$f=\exp \circ \phi $
. Since a holomorphic homeomorphism of the complex plane must be a linear map, we thus have
where
![]() $A(\neq 0)$
and B are complex constants. This completes the proof.
$A(\neq 0)$
and B are complex constants. This completes the proof.
It follows immediately that if
![]() $f\in \operatorname {\mathcal {S}}_{2}$
, then the singular values of f are both asymptotic values. Moreover, if one of the asymptotic values is at
$f\in \operatorname {\mathcal {S}}_{2}$
, then the singular values of f are both asymptotic values. Moreover, if one of the asymptotic values is at
![]() $\infty $
, then f is of the form
$\infty $
, then f is of the form
![]() $\unicode{x3bb} e^{z}$
; if both of them are finite, then f can be written as
$\unicode{x3bb} e^{z}$
; if both of them are finite, then f can be written as
![]() $M(e^{z})$
where M is Möbius, sending
$M(e^{z})$
where M is Möbius, sending
![]() $0$
and
$0$
and
![]() $\infty $
to two finite points. This, together with the results obtained in [Reference Galazka and KotusGK18, Reference McMullenMcM87], shows that Theorem A holds; see also [Reference CuiCui21a].
$\infty $
to two finite points. This, together with the results obtained in [Reference Galazka and KotusGK18, Reference McMullenMcM87], shows that Theorem A holds; see also [Reference CuiCui21a].

Figure 1 Producing meromorphic functions in
![]() $\operatorname {\mathcal {S}}_{3}$
by using line complexes. Replacing the dashed line in the left picture by any one of the finite graphs on the right or any finite combination of these graphs will give functions with three singular values which are not topologically equivalent.
$\operatorname {\mathcal {S}}_{3}$
by using line complexes. Replacing the dashed line in the left picture by any one of the finite graphs on the right or any finite combination of these graphs will give functions with three singular values which are not topologically equivalent.
The next natural step would be to ask if a similar result stated in Theorem 2.1 will hold if one has more singular values. This need not be true. In fact, even for meromorphic functions with three singular values, one cannot expect a similar function-theoretic rigidity to that of Theorem 2.1. Recent work of Bishop [Reference BishopBis15] shows that there are uncountably many essentially different entire functions with two critical values. More precisely, the classes of topologically equivalent entire functions with two critical values are uncountable. See also [Reference CuiCui21a]. One can also use the so-called Maclane–Vinberg method to construct entire functions with two singular values; see [Reference Bergweiler, Fagella and Rempe-GillenBFRG15, Observation 5.2]. For general meromorphic functions with three singular values, one can resort to the theory of line complexes to construct such functions; see [Reference Goldberg and OstrovskiiGO08, Ch. 7]. Without giving a detailed account of line complexes, we mention that one can show that there exist infinitely many non-equivalent meromorphic functions in
![]() $\operatorname {\mathcal {S}}_{3}$
by modifying the left graph in Figure 1: Replacing the dashed line by one of finite graphs shown on the right of Figure 1 will produce meromorphic functions with three singular values. It is clear that there are infinitely many such functions, since one can consider any finite combination of these finite graphs which are then used to replace the dashed line. The meromorphic functions produced are those with rational Schwarzian derivatives. For a complete treatment of these functions, we refer to [Reference Goldberg and OstrovskiiGO08, Ch. 7] and [Reference ElfvingElf34].
$\operatorname {\mathcal {S}}_{3}$
by modifying the left graph in Figure 1: Replacing the dashed line by one of finite graphs shown on the right of Figure 1 will produce meromorphic functions with three singular values. It is clear that there are infinitely many such functions, since one can consider any finite combination of these finite graphs which are then used to replace the dashed line. The meromorphic functions produced are those with rational Schwarzian derivatives. For a complete treatment of these functions, we refer to [Reference Goldberg and OstrovskiiGO08, Ch. 7] and [Reference ElfvingElf34].
3. The construction
For
![]() $\delta \in (0,2\pi ]$
, put
$\delta \in (0,2\pi ]$
, put
In particular, if
![]() $\delta =2\pi $
, then
$\delta =2\pi $
, then
![]() $\operatorname {\mathbb C}_{\delta }$
is the slit plane
$\operatorname {\mathbb C}_{\delta }$
is the slit plane
![]() $\operatorname {\mathbb C}\setminus \mathbb {R}^{+}$
. Choosing the natural branch of the logarithm, for any
$\operatorname {\mathbb C}\setminus \mathbb {R}^{+}$
. Choosing the natural branch of the logarithm, for any
![]() $\alpha \in (0,2\pi ]$
, we set
$\alpha \in (0,2\pi ]$
, we set
 $$ \begin{align*} h:\,\operatorname{\mathbb C}_{2\pi}&\to\operatorname{\mathbb C}_{\alpha},\\ z&\mapsto z^{\alpha/2\pi} \end{align*} $$
$$ \begin{align*} h:\,\operatorname{\mathbb C}_{2\pi}&\to\operatorname{\mathbb C}_{\alpha},\\ z&\mapsto z^{\alpha/2\pi} \end{align*} $$
which then defines a conformal map.
To construct meromorphic functions in
![]() $\operatorname {\mathcal {S}}_{4}$
, we will consider the restriction of some carefully chosen Weierstraß elliptic function
$\operatorname {\mathcal {S}}_{4}$
, we will consider the restriction of some carefully chosen Weierstraß elliptic function
![]() $\wp $
in the sector domain
$\wp $
in the sector domain
![]() $\operatorname {\mathbb C}_{\alpha }$
. Then the function defined as
$\operatorname {\mathbb C}_{\alpha }$
. Then the function defined as
![]() $\wp \circ h$
will be meromorphic in
$\wp \circ h$
will be meromorphic in
![]() $\operatorname {\mathbb C}_{2\pi }$
. We will then need to extend this function across the positive real axis in order to have a meromorphic function in the plane. However, the extension need not be continuous; in other words, for
$\operatorname {\mathbb C}_{2\pi }$
. We will then need to extend this function across the positive real axis in order to have a meromorphic function in the plane. However, the extension need not be continuous; in other words, for
![]() $x\in \mathbb {R}^{+}$
,
$x\in \mathbb {R}^{+}$
,
![]() $\wp \circ h (x)$
need not coincide when one approaches x respectively from the upper and lower half planes. This will be resolved by introducing a spiral map and then using a quasiconformal surgery. See Figure 2 for an illustration.
$\wp \circ h (x)$
need not coincide when one approaches x respectively from the upper and lower half planes. This will be resolved by introducing a spiral map and then using a quasiconformal surgery. See Figure 2 for an illustration.

Figure 2 Illustration of the construction. We have put
![]() $\eta =\alpha \mu /(2\pi )$
. The map
$\eta =\alpha \mu /(2\pi )$
. The map
![]() $\Phi $
is quasiconformal, which helps to remove the discontinuity arising on the logarithmic spiral
$\Phi $
is quasiconformal, which helps to remove the discontinuity arising on the logarithmic spiral
![]() $\Gamma $
.
$\Gamma $
.
Remark 3.1. The spiral map we will introduce will help us to achieve every possible finite order. In a recent paper [Reference Bergweiler and EremenkoBE17], Bergweiler and Eremenko also used this idea to solve an open problem in the theory of complex differential equations.
From now on we fix one
![]() $\alpha $
and use the corresponding function h as defined above. Then in the sector
$\alpha $
and use the corresponding function h as defined above. Then in the sector
![]() $\operatorname {\mathbb C}_{\alpha }$
we consider a Weierstraß elliptic function
$\operatorname {\mathbb C}_{\alpha }$
we consider a Weierstraß elliptic function
![]() $\wp $
with two periods
$\wp $
with two periods
![]() $1$
and
$1$
and
![]() $\tau $
, where
$\tau $
, where
![]() $\tau $
will satisfy the following condition:
$\tau $
will satisfy the following condition:
 $$ \begin{align} \arg\tau= \begin{cases} ~\alpha&\text{if } \alpha<\pi,\\ ~\alpha-\pi&\text{if }\alpha>\pi. \end{cases} \end{align} $$
$$ \begin{align} \arg\tau= \begin{cases} ~\alpha&\text{if } \alpha<\pi,\\ ~\alpha-\pi&\text{if }\alpha>\pi. \end{cases} \end{align} $$
When
![]() $\alpha =\pi $
, the function defined as
$\alpha =\pi $
, the function defined as
![]() $\wp \circ h$
extends continuously across the positive real axis and thus gives a function meromorphic in the plane (which is actually
$\wp \circ h$
extends continuously across the positive real axis and thus gives a function meromorphic in the plane (which is actually
![]() $\wp (\sqrt {z})$
). This is an easy case to deal with, so we will assume in what follows that
$\wp (\sqrt {z})$
). This is an easy case to deal with, so we will assume in what follows that
![]() $\alpha \neq \pi $
. The main point of condition (3.1) is to make sure that the two prime periods of the chosen Weierstraß
$\alpha \neq \pi $
. The main point of condition (3.1) is to make sure that the two prime periods of the chosen Weierstraß
![]() $\wp $
-function lie on two boundaries of
$\wp $
-function lie on two boundaries of
![]() $\operatorname {\mathbb C}_{\alpha }$
. Now we put
$\operatorname {\mathbb C}_{\alpha }$
. Now we put
 $$ \begin{align*}e_{1}=\wp\bigg(\frac{1}{2}\bigg),\quad e_{2}=\wp\bigg(\frac{1+\tau}{2}\bigg),\quad e_{3}=\wp\bigg(\frac{\tau}{2}\bigg),\end{align*} $$
$$ \begin{align*}e_{1}=\wp\bigg(\frac{1}{2}\bigg),\quad e_{2}=\wp\bigg(\frac{1+\tau}{2}\bigg),\quad e_{3}=\wp\bigg(\frac{\tau}{2}\bigg),\end{align*} $$
which are finite critical values of
![]() $\wp $
(with another critical value at
$\wp $
(with another critical value at
![]() $\infty $
).
$\infty $
).
One can then see immediately that
is well defined and meromorphic in the slit plane. However,
![]() $g_{1}$
may not be able to extend continuously across the positive real axis, as we mentioned above. One of the main objectives in the construction we will make is to circumvent this problem.
$g_{1}$
may not be able to extend continuously across the positive real axis, as we mentioned above. One of the main objectives in the construction we will make is to circumvent this problem.
By choosing the natural branch of the power map, let
It can readily be seen that if
![]() $\mu $
has real part equal to
$\mu $
has real part equal to
![]() $1$
then the image of
$1$
then the image of
![]() $\operatorname {\mathbb C}\setminus \mathbb {R}^{+} $
is an open set whose complement is a logarithmic spiral. Let us denote this spiral by
$\operatorname {\mathbb C}\setminus \mathbb {R}^{+} $
is an open set whose complement is a logarithmic spiral. Let us denote this spiral by
![]() $\Gamma $
. Now note that if
$\Gamma $
. Now note that if
![]() $\{x_{n}\}_{n=0}^{\infty }$
and
$\{x_{n}\}_{n=0}^{\infty }$
and
![]() $\{y_{n}\}_{n=0}^{\infty }$
are two sequences of complex numbers approaching a point
$\{y_{n}\}_{n=0}^{\infty }$
are two sequences of complex numbers approaching a point
![]() $z \in \mathbb {R}^{+}$
from different sides of the real axis, the limits of
$z \in \mathbb {R}^{+}$
from different sides of the real axis, the limits of
![]() $p(x_{n})$
and
$p(x_{n})$
and
![]() $p(y_{n})$
as
$p(y_{n})$
as
![]() $n \rightarrow \infty $
may well be different. So the map p may not have a continuous extension to
$n \rightarrow \infty $
may well be different. So the map p may not have a continuous extension to
![]() $\mathbb {R}^{+}$
. For our purposes, we put
$\mathbb {R}^{+}$
. For our purposes, we put
 $$ \begin{align*} \mu=1-i\,\frac{\log|\tau|}{\alpha}. \end{align*} $$
$$ \begin{align*} \mu=1-i\,\frac{\log|\tau|}{\alpha}. \end{align*} $$
Denote by q the inverse of p; that is,
![]() $q(z)=z^{\mu }$
. Then the function
$q(z)=z^{\mu }$
. Then the function
 $$ \begin{align*} g_{2}: \operatorname{\mathbb C}\setminus\Gamma &\to\operatorname{\mathbb C}_{2\pi},\\ z&\mapsto g_{1}(q(z)) \end{align*} $$
$$ \begin{align*} g_{2}: \operatorname{\mathbb C}\setminus\Gamma &\to\operatorname{\mathbb C}_{2\pi},\\ z&\mapsto g_{1}(q(z)) \end{align*} $$
is well defined and meromorphic in the complement of a logarithmic spiral
![]() $\Gamma $
. It may not extend continuously across
$\Gamma $
. It may not extend continuously across
![]() $\Gamma $
, but by the choice of
$\Gamma $
, but by the choice of
![]() $\mu $
and
$\mu $
and
![]() $\tau $
, with a simple computation, we can extend
$\tau $
, with a simple computation, we can extend
![]() $g_{2}$
continuously to a discrete set of
$g_{2}$
continuously to a discrete set of
![]() $\Gamma $
whose points will be mapped by
$\Gamma $
whose points will be mapped by
![]() $h\circ q$
to poles of
$h\circ q$
to poles of
![]() $\wp $
. We show below how to remove the discontinuities between this discrete set of points on
$\wp $
. We show below how to remove the discontinuities between this discrete set of points on
![]() $\Gamma $
by using a quasiconformal surgery. In short, we will construct a quasiconformal self-map
$\Gamma $
by using a quasiconformal surgery. In short, we will construct a quasiconformal self-map
![]() $\Phi $
of
$\Phi $
of
![]() $\operatorname {\mathbb C}_{\alpha }$
such that the new defined function
$\operatorname {\mathbb C}_{\alpha }$
such that the new defined function
![]() $\wp \circ \Phi \circ h\circ q$
extends continuously across
$\wp \circ \Phi \circ h\circ q$
extends continuously across
![]() $\Gamma $
.
$\Gamma $
.
Let P denote the parallelogram formed by four vertices
![]() $0,\,1/2,\,(1+\tau )/2$
and
$0,\,1/2,\,(1+\tau )/2$
and
![]() $\tau /2$
. It follows from the basic properties of Weierstraß elliptic functions that
$\tau /2$
. It follows from the basic properties of Weierstraß elliptic functions that
![]() $\delta :=\wp (\partial P)$
is a simple closed curve on
$\delta :=\wp (\partial P)$
is a simple closed curve on
![]() $\operatorname {\widehat {\mathbb C}}$
, which passes through
$\operatorname {\widehat {\mathbb C}}$
, which passes through
![]() $\infty $
on both sides such that
$\infty $
on both sides such that
 $\operatorname {\widehat {\mathbb C}}\setminus \delta $
consists of two domains A and B. Suppose without loss of generality that
$\operatorname {\widehat {\mathbb C}}\setminus \delta $
consists of two domains A and B. Suppose without loss of generality that
![]() $A=\wp (P)$
. Note that all critical values of
$A=\wp (P)$
. Note that all critical values of
![]() $\wp $
lie on
$\wp $
lie on
![]() $\delta $
. Now we can choose an analytic closed curve
$\delta $
. Now we can choose an analytic closed curve
![]() $\gamma $
in
$\gamma $
in
![]() $\operatorname {\widehat {\mathbb C}}$
such that
$\operatorname {\widehat {\mathbb C}}$
such that
![]() $\gamma \cap \delta =\{e_{2},\,\infty \}$
. To achieve this, we first choose an analytic curve
$\gamma \cap \delta =\{e_{2},\,\infty \}$
. To achieve this, we first choose an analytic curve
![]() $\gamma _{1}$
lying entirely in A with two endpoints being
$\gamma _{1}$
lying entirely in A with two endpoints being
![]() $e_{2}$
and
$e_{2}$
and
![]() $\infty $
; similarly, an analytic curve
$\infty $
; similarly, an analytic curve
![]() $\gamma _{2}$
is chosen to lie completely in B with two endpoints
$\gamma _{2}$
is chosen to lie completely in B with two endpoints
![]() $e_{2}$
and
$e_{2}$
and
![]() $\infty $
. Then
$\infty $
. Then
![]() $\gamma $
is defined as the union of
$\gamma $
is defined as the union of
![]() $\gamma _{1}$
and
$\gamma _{1}$
and
![]() $\gamma _{2}$
together with their common endpoints. See Figure 3 for an illustration. Now we consider suitable preimage of
$\gamma _{2}$
together with their common endpoints. See Figure 3 for an illustration. Now we consider suitable preimage of
![]() $\gamma $
under the function
$\gamma $
under the function
![]() $\wp $
. More precisely, we have the following result; compare this with Proposition 3.1 of [Reference Aspenberg and CuiAC21]. Put
$\wp $
. More precisely, we have the following result; compare this with Proposition 3.1 of [Reference Aspenberg and CuiAC21]. Put
 $$ \begin{align*}c=\dfrac{1+\tau}{2}.\end{align*} $$
$$ \begin{align*}c=\dfrac{1+\tau}{2}.\end{align*} $$
Proposition 3.1. Let
![]() $\gamma $
be as above. Then there exist two piecewise analytic curves
$\gamma $
be as above. Then there exist two piecewise analytic curves
![]() $\beta _{i}$
with
$\beta _{i}$
with
![]() $\wp (\beta _{i})=\gamma $
for all i, such that the following assertions hold.
$\wp (\beta _{i})=\gamma $
for all i, such that the following assertions hold.

Figure 3 The curve
![]() $\gamma $
is chosen such that it passes through the critical value
$\gamma $
is chosen such that it passes through the critical value
![]() $e_{2}$
and
$e_{2}$
and
![]() $\infty $
. Then we choose two suitable preimages
$\infty $
. Then we choose two suitable preimages
![]() $\beta _{1}$
and
$\beta _{1}$
and
![]() $\beta _{2}$
of
$\beta _{2}$
of
![]() $\gamma $
such that they are periodic and both start from c, which is a preimage of the critical value
$\gamma $
such that they are periodic and both start from c, which is a preimage of the critical value
![]() $e_{2}$
.
$e_{2}$
.
-
•
 $\beta _{1}\cap \beta _{2}=\{c\}$
.
$\beta _{1}\cap \beta _{2}=\{c\}$
. -
•
 $\beta _{1}$
starts from the point c and is periodic with period
$\beta _{1}$
starts from the point c and is periodic with period
 $1$
, that is,
$1$
, that is,
 $z\in \beta _{1}$
implies that
$z\in \beta _{1}$
implies that
 $z+1\in \beta _{1}$
. Moreover,
$z+1\in \beta _{1}$
. Moreover,
 $\beta _{1}$
passes through poles at n of
$\beta _{1}$
passes through poles at n of
 $\wp $
for all
$\wp $
for all
 $n\geq 1$
.
$n\geq 1$
. -
•
 $\beta _{2}$
starts from c and is periodic with period
$\beta _{2}$
starts from c and is periodic with period
 $\tau $
, that is,
$\tau $
, that is,
 $z\in \beta _{2}$
implies that
$z\in \beta _{2}$
implies that
 $z+\tau \in \beta _{2}$
. Moreover,
$z+\tau \in \beta _{2}$
. Moreover,
 $\beta _{2}$
passes through poles
$\beta _{2}$
passes through poles
 $n\tau $
for all
$n\tau $
for all
 $n\geq 1$
.
$n\geq 1$
.
Proof. For convenience, we put
![]() $\gamma _{1}=\gamma \cap A$
and
$\gamma _{1}=\gamma \cap A$
and
![]() $\gamma _{2}=\gamma \cap B$
. We will use
$\gamma _{2}=\gamma \cap B$
. We will use
![]() $W+c$
as the translation by a complex number c for any set
$W+c$
as the translation by a complex number c for any set
![]() $W\subset \operatorname {\mathbb C}$
; in other words,
$W\subset \operatorname {\mathbb C}$
; in other words,
![]() $W+c=\{z+c: z\in W\}$
. Recall that P is the parallelogram formed by four points
$W+c=\{z+c: z\in W\}$
. Recall that P is the parallelogram formed by four points
![]() $0,\,1/2,\,(1+\tau )/2$
and
$0,\,1/2,\,(1+\tau )/2$
and
![]() $\tau /2$
. Now by elementary properties of Weierstraß elliptic functions we know that
$\tau /2$
. Now by elementary properties of Weierstraß elliptic functions we know that
 $\wp : P+\tfrac 12\to B$
is conformal. Therefore,
$\wp : P+\tfrac 12\to B$
is conformal. Therefore,
![]() $\gamma _{2}$
has a preimage denoted by
$\gamma _{2}$
has a preimage denoted by
![]() $\beta ^{1}_{1}$
in
$\beta ^{1}_{1}$
in
![]() $P+1/2$
which is an analytic curve connecting
$P+1/2$
which is an analytic curve connecting
![]() $(1+\tau )/2$
and
$(1+\tau )/2$
and
![]() $1$
. The latter property follows easily since
$1$
. The latter property follows easily since
![]() $\gamma _{2}\subset B$
connects
$\gamma _{2}\subset B$
connects
![]() $e_{2}$
and
$e_{2}$
and
![]() $\infty $
. Similarly, since
$\infty $
. Similarly, since
![]() $\wp : P+1\to A$
is conformal we see immediately that
$\wp : P+1\to A$
is conformal we see immediately that
![]() $\gamma _{1}$
has a preimage
$\gamma _{1}$
has a preimage
![]() $\beta ^{2}_{1}$
in
$\beta ^{2}_{1}$
in
![]() $P+1$
which is an analytic curve connecting
$P+1$
which is an analytic curve connecting
![]() $1$
and
$1$
and
![]() $(3+\tau )/2$
. Now by periodicity of
$(3+\tau )/2$
. Now by periodicity of
![]() $\wp $
, the curve
$\wp $
, the curve
 $\beta ^{1}_{1}\cup \beta ^{2}_{1}$
and its translations by
$\beta ^{1}_{1}\cup \beta ^{2}_{1}$
and its translations by
![]() $n\in \mathbb {N}$
will be mapped conformally onto
$n\in \mathbb {N}$
will be mapped conformally onto
![]() $\beta $
. Now we define
$\beta $
. Now we define
 $$ \begin{align*}\beta_{1}=\bigcup_{n\geq 0}(\beta^{1}_{1}\cup\beta^{2}_{1} + n).\end{align*} $$
$$ \begin{align*}\beta_{1}=\bigcup_{n\geq 0}(\beta^{1}_{1}\cup\beta^{2}_{1} + n).\end{align*} $$
It is clear that
![]() $\beta _{1}$
satisfies all the required properties.
$\beta _{1}$
satisfies all the required properties.
In the same way we can define
![]() $\beta _{2}$
as claimed. We omit the details here.
$\beta _{2}$
as claimed. We omit the details here.
We denote by V the domain contained in
![]() $\operatorname {\mathbb C}_{\alpha }$
and bounded by
$\operatorname {\mathbb C}_{\alpha }$
and bounded by
![]() $\beta _{1}$
and
$\beta _{1}$
and
![]() $\beta _{2}$
. In what follows we concentrate on the construction of a quasiconformal mapping
$\beta _{2}$
. In what follows we concentrate on the construction of a quasiconformal mapping
such that the function
![]() $\wp \circ \Phi \circ h\circ q$
extends continuously across the logarithmic spiral
$\wp \circ \Phi \circ h\circ q$
extends continuously across the logarithmic spiral
![]() $\Gamma $
and thus gives a function continuous throughout the whole plane. See Figure 4 for the construction of
$\Gamma $
and thus gives a function continuous throughout the whole plane. See Figure 4 for the construction of
![]() $\Phi $
.
$\Phi $
.

Figure 4 Sketch of the construction of the quasiconformal map
![]() $\Phi $
.
$\Phi $
.
![]() $S^{\prime }_{1}$
and
$S^{\prime }_{1}$
and
![]() $S^{\prime }_{2}$
are the restrictions of
$S^{\prime }_{2}$
are the restrictions of
![]() $S_{1}$
and
$S_{1}$
and
![]() $S_{2}$
to the sector
$S_{2}$
to the sector
![]() $\operatorname {\mathbb C}_{\alpha }$
, while
$\operatorname {\mathbb C}_{\alpha }$
, while
![]() $T^{\prime }_{1}$
and
$T^{\prime }_{1}$
and
![]() $T^{\prime }_{2}$
are the corresponding images of
$T^{\prime }_{2}$
are the corresponding images of
![]() $S^{\prime }_{1}$
and
$S^{\prime }_{1}$
and
![]() $S^{\prime }_{2}$
under the maps
$S^{\prime }_{2}$
under the maps
![]() $\phi _{1,1}$
and
$\phi _{1,1}$
and
![]() $\phi _{1,2}$
. The same applies to
$\phi _{1,2}$
. The same applies to
![]() $\widehat {S}^{\prime }_{1}$
,
$\widehat {S}^{\prime }_{1}$
,
![]() $\widehat {S}^{\prime }_{2}$
and
$\widehat {S}^{\prime }_{2}$
and
 $\widehat {T}^{\prime }_{1},\,\widehat {T}^{\prime }_{2}$
.
$\widehat {T}^{\prime }_{1},\,\widehat {T}^{\prime }_{2}$
.
By periodicity of Weierstraß elliptic functions and the construction of
![]() $\beta _{1}$
, we can define a periodic curve
$\beta _{1}$
, we can define a periodic curve
![]() $\tilde {\beta }_{1}$
which is the extension of
$\tilde {\beta }_{1}$
which is the extension of
![]() $\beta _{1}$
along the direction of the negative real axis. Now choose a real number
$\beta _{1}$
along the direction of the negative real axis. Now choose a real number
![]() $a>0$
such that
$a>0$
such that
![]() $a>\max _{z\in \tilde {\beta }_{1}}\operatorname {Im}(z)$
. Define
$a>\max _{z\in \tilde {\beta }_{1}}\operatorname {Im}(z)$
. Define
 $$ \begin{align*}T_{1}=\{z:\,\operatorname{Im}_{\substack{w\in\tilde{\beta}_{1}}, \,\substack{\operatorname{Re} w=\operatorname{Re} z}}(w)<\operatorname{Im}(z)<a\}.\end{align*} $$
$$ \begin{align*}T_{1}=\{z:\,\operatorname{Im}_{\substack{w\in\tilde{\beta}_{1}}, \,\substack{\operatorname{Re} w=\operatorname{Re} z}}(w)<\operatorname{Im}(z)<a\}.\end{align*} $$
Then by [Reference Aspenberg and CuiAC21, Lemma 3.1], there is a real number
![]() $a^{\prime }>0$
such that with
$a^{\prime }>0$
such that with
there is a conformal map
which fixes three boundary points
![]() $0$
and
$0$
and
![]() $\pm \infty $
and is periodic with period
$\pm \infty $
and is periodic with period
![]() $1$
. In other words,
$1$
. In other words,
for any
![]() $z\in S_{1}$
. Moreover,
$z\in S_{1}$
. Moreover,
![]() $\phi _{1,1}$
extends to the boundary as a piecewise diffeomorphism.
$\phi _{1,1}$
extends to the boundary as a piecewise diffeomorphism.
Choose another real number b satisfying
![]() $b>\max \{a,\,a^{\prime }\}$
and put
$b>\max \{a,\,a^{\prime }\}$
and put
and
We now want to define a quasiconformal map from
![]() $S_{2}$
to
$S_{2}$
to
![]() $T_{2}$
which interpolates between the identity map on the upper boundary of
$T_{2}$
which interpolates between the identity map on the upper boundary of
![]() $S_{2}$
and the extension of
$S_{2}$
and the extension of
![]() $\phi _{1,1}$
on the lower boundary of
$\phi _{1,1}$
on the lower boundary of
![]() $S_{2}$
. For convenience, we denote by
$S_{2}$
. For convenience, we denote by
![]() $\ell _{1}$
the horizontal curve
$\ell _{1}$
the horizontal curve
![]() $\{z: \operatorname {Im}(z)=a\}$
and by
$\{z: \operatorname {Im}(z)=a\}$
and by
![]() $\tilde {\ell }_{1}$
the curve
$\tilde {\ell }_{1}$
the curve
![]() $\{z: \operatorname {Im}(z)=a^{\prime }\}$
. We also put
$\{z: \operatorname {Im}(z)=a^{\prime }\}$
. We also put
![]() $\ell _{2}=\{z:\operatorname {Im}(z)=b\}$
. Suppose that
$\ell _{2}=\{z:\operatorname {Im}(z)=b\}$
. Suppose that
![]() $\chi _{1}$
is the boundary extension of
$\chi _{1}$
is the boundary extension of
![]() $\phi _{1,1}$
to
$\phi _{1,1}$
to
![]() $\tilde {\ell }_{1}$
. Then it follows from the construction of
$\tilde {\ell }_{1}$
. Then it follows from the construction of
![]() $\phi _{1,1}$
, and the Schwarz reflection principle (and the fact that
$\phi _{1,1}$
, and the Schwarz reflection principle (and the fact that
![]() $\tilde {\ell }_{1}$
and
$\tilde {\ell }_{1}$
and
![]() $\ell _{1}$
are straight lines), that
$\ell _{1}$
are straight lines), that
![]() $\chi _{1}:\tilde {\ell }_{1}\to \ell _{1}$
is analytic. Moreover,
$\chi _{1}:\tilde {\ell }_{1}\to \ell _{1}$
is analytic. Moreover,
![]() $\chi _{1}(z+1)=\chi _{1}(z)+1$
for
$\chi _{1}(z+1)=\chi _{1}(z)+1$
for
![]() $z\in \mathbb {R}$
. By considering
$z\in \mathbb {R}$
. By considering
we see that
![]() $\widetilde {\chi }_{1}: \mathbb {R}\to \mathbb {R}$
is increasing and analytic. We also define
$\widetilde {\chi }_{1}: \mathbb {R}\to \mathbb {R}$
is increasing and analytic. We also define
Note that
![]() $\widetilde {\chi }_{1}$
is obtained from
$\widetilde {\chi }_{1}$
is obtained from
![]() $\chi _{1}$
and the identity map by moving the lower boundaries of
$\chi _{1}$
and the identity map by moving the lower boundaries of
![]() $S_{2}$
and
$S_{2}$
and
![]() $T_{2}$
to the real axis. Suppose the new strips are
$T_{2}$
to the real axis. Suppose the new strips are
![]() $S^{\prime \prime }_{2}$
and
$S^{\prime \prime }_{2}$
and
![]() $T^{\prime \prime }_{2}$
, respectively. Then
$T^{\prime \prime }_{2}$
, respectively. Then
 $$ \begin{align*}L(x+iy)=\bigg(1-\frac{y}{b-a^{\prime}}\bigg)\widetilde{\chi}_{1}(x)+\frac{y}{b-a^{\prime}}\widetilde{\chi}_{2}(x)+i\,\frac{b-a}{b-a^{\prime}}y\end{align*} $$
$$ \begin{align*}L(x+iy)=\bigg(1-\frac{y}{b-a^{\prime}}\bigg)\widetilde{\chi}_{1}(x)+\frac{y}{b-a^{\prime}}\widetilde{\chi}_{2}(x)+i\,\frac{b-a}{b-a^{\prime}}y\end{align*} $$
is the linear interpolation between
![]() $\widetilde {\chi }_{1}$
and
$\widetilde {\chi }_{1}$
and
![]() $\widetilde {\chi }_{2}$
. This is actually a quasiconformal map, as can be seen by checking the Jacobian of L, which is
$\widetilde {\chi }_{2}$
. This is actually a quasiconformal map, as can be seen by checking the Jacobian of L, which is
 $$ \begin{align*}\frac{b-a}{b-a^{\prime}}\bigg(\bigg(1-\frac{y}{b-a^{\prime}}\bigg)\widetilde{\chi}^{\prime}_{1}(x)+\frac{y}{b-a^{\prime}}\widetilde{\chi}^{\prime}_{2}(x)\bigg).\end{align*} $$
$$ \begin{align*}\frac{b-a}{b-a^{\prime}}\bigg(\bigg(1-\frac{y}{b-a^{\prime}}\bigg)\widetilde{\chi}^{\prime}_{1}(x)+\frac{y}{b-a^{\prime}}\widetilde{\chi}^{\prime}_{2}(x)\bigg).\end{align*} $$
It is strictly bigger than zero since both
![]() $\widetilde {\chi }_{1}$
and
$\widetilde {\chi }_{1}$
and
![]() $\widetilde {\chi }_{2}$
are increasing. Together with the periodicity, this implies that L is quasiconformal. Now we define
$\widetilde {\chi }_{2}$
are increasing. Together with the periodicity, this implies that L is quasiconformal. Now we define
 $$ \begin{align*} \phi_{1,2}: S_{2} &\to T_{2},\\ z&\mapsto L(z-ia^{\prime})+ia. \end{align*} $$
$$ \begin{align*} \phi_{1,2}: S_{2} &\to T_{2},\\ z&\mapsto L(z-ia^{\prime})+ia. \end{align*} $$
This is a quasiconformal map.
Along the
![]() $\tau $
-direction, we use a similar idea to that above to obtain a quasiconformal map. More precisely, we first consider a periodic curve
$\tau $
-direction, we use a similar idea to that above to obtain a quasiconformal map. More precisely, we first consider a periodic curve
![]() $\tilde {\beta }_{2}$
which is the natural extension of
$\tilde {\beta }_{2}$
which is the natural extension of
![]() $\beta _{2}$
. With
$\beta _{2}$
. With
we define, for some real numbers
![]() $c^{\prime },\,c$
and d, where
$c^{\prime },\,c$
and d, where
![]() $c= (1+\tau )/2$
and
$c= (1+\tau )/2$
and
![]() $c^{\prime },d$
will be determined later,
$c^{\prime },d$
will be determined later,
 $$ \begin{align*} \widetilde{\widehat{\ell}}_{1}&=\ell+c^{\prime}, \nonumber\\ \widehat{\ell}_{1}&=\ell+c, \nonumber \\ \widehat{\ell}_{2}&=\ell+d. \end{align*} $$
$$ \begin{align*} \widetilde{\widehat{\ell}}_{1}&=\ell+c^{\prime}, \nonumber\\ \widehat{\ell}_{1}&=\ell+c, \nonumber \\ \widehat{\ell}_{2}&=\ell+d. \end{align*} $$
We also denote by
![]() $\widehat {S}_{1}$
the strip between
$\widehat {S}_{1}$
the strip between
![]() $\ell $
and
$\ell $
and
![]() $\widetilde{\widehat{\ell }}_{1}$
, and by
$\widetilde{\widehat{\ell }}_{1}$
, and by
![]() $\widehat {T}_{1}$
the domain bounded by
$\widehat {T}_{1}$
the domain bounded by
![]() $\tilde {\beta }_{2}$
and
$\tilde {\beta }_{2}$
and
![]() $\widehat {\ell }_{1}$
. Moreover,
$\widehat {\ell }_{1}$
. Moreover,
![]() $\widehat {S}_{2}$
will be the strip bounded by
$\widehat {S}_{2}$
will be the strip bounded by
![]() $\widetilde{\widehat{\ell }}_{1}$
and
$\widetilde{\widehat{\ell }}_{1}$
and
![]() $\widehat {\ell }_{2}$
, while
$\widehat {\ell }_{2}$
, while
![]() $\widehat {T}_{2}$
is bounded by
$\widehat {T}_{2}$
is bounded by
![]() $\widehat {\ell }_{1}$
and
$\widehat {\ell }_{1}$
and
![]() $\widehat {\ell }_{2}$
.
$\widehat {\ell }_{2}$
.
Now
![]() $c^{\prime }$
and c are chosen (similarly to
$c^{\prime }$
and c are chosen (similarly to
![]() $a^{\prime }$
and a above) such that there exists a conformal map
$a^{\prime }$
and a above) such that there exists a conformal map
 $$ \begin{align*}\phi_{2,1}: \widehat{S}_{1}\to\widehat{T}_{1}\end{align*} $$
$$ \begin{align*}\phi_{2,1}: \widehat{S}_{1}\to\widehat{T}_{1}\end{align*} $$
which is periodic with period
![]() $\tau $
and fixes three boundary points
$\tau $
and fixes three boundary points
![]() $0$
and
$0$
and
![]() $\pm \infty $
(here
$\pm \infty $
(here
![]() $\pm \infty $
are understood as infinity along two directions of
$\pm \infty $
are understood as infinity along two directions of
![]() $\ell $
). In the same way as the map
$\ell $
). In the same way as the map
![]() $\phi _{1,2}$
was defined, we can define a quasiconformal map
$\phi _{1,2}$
was defined, we can define a quasiconformal map
 $$ \begin{align*}\phi_{2,2}: \widehat{S}_{2}\to\widehat{T}_{2}.\end{align*} $$
$$ \begin{align*}\phi_{2,2}: \widehat{S}_{2}\to\widehat{T}_{2}.\end{align*} $$
We omit the details here. For later purposes, we put
and

Moreover,
We now consider restrictions of the maps constructed above on the domain
![]() $\operatorname {\mathbb C}_{\alpha }$
. More precisely, we define
$\operatorname {\mathbb C}_{\alpha }$
. More precisely, we define
 $$ \begin{align*} \begin{aligned} \phi_{1}: S &\longrightarrow T;~\,~ z\longmapsto \begin{cases} ~\phi_{1,1}(z)&\text{if } z\in S_{1},\\ ~\phi_{1,2}(z)&\text{if } z\in S_{2}. \end{cases} \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \phi_{1}: S &\longrightarrow T;~\,~ z\longmapsto \begin{cases} ~\phi_{1,1}(z)&\text{if } z\in S_{1},\\ ~\phi_{1,2}(z)&\text{if } z\in S_{2}. \end{cases} \end{aligned} \end{align*} $$
In a similar way, we have
 $$ \begin{align*} \begin{aligned} \phi_{2}: \widehat{S} &\longrightarrow \widehat{T};~\,~z\longmapsto \begin{cases} ~\phi_{2,1}(z)&\text{if } z\in \widehat{S}_{1},\\ ~\phi_{2,2}(z)&\text{if } z\in \widehat{S}_{2}. \end{cases} \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \phi_{2}: \widehat{S} &\longrightarrow \widehat{T};~\,~z\longmapsto \begin{cases} ~\phi_{2,1}(z)&\text{if } z\in \widehat{S}_{1},\\ ~\phi_{2,2}(z)&\text{if } z\in \widehat{S}_{2}. \end{cases} \end{aligned} \end{align*} $$
Finally, we define
 $$ \begin{align*} \begin{aligned} \phi_{3}: V_{\alpha} &\longrightarrow V_{\alpha},\\ z&\longmapsto z. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \phi_{3}: V_{\alpha} &\longrightarrow V_{\alpha},\\ z&\longmapsto z. \end{aligned} \end{align*} $$
Note that the half-strips S and
![]() $\widehat {S}$
overlap on a parallelogram
$\widehat {S}$
overlap on a parallelogram
which contains the origin on the boundary. Both
![]() $\phi _{1}$
and
$\phi _{1}$
and
![]() $\phi _{2}$
are defined on Q, but they do not necessarily coincide there. Away from Q, in
$\phi _{2}$
are defined on Q, but they do not necessarily coincide there. Away from Q, in
![]() $\operatorname {\mathbb C}_{\alpha }\setminus Q$
we have a well-defined quasiconformal map, which is
$\operatorname {\mathbb C}_{\alpha }\setminus Q$
we have a well-defined quasiconformal map, which is
![]() $\phi _{1}$
in
$\phi _{1}$
in
![]() $S\setminus Q$
,
$S\setminus Q$
,
![]() $\phi _{2}$
in
$\phi _{2}$
in
 $\widehat {S}\setminus Q$
and the identity on
$\widehat {S}\setminus Q$
and the identity on
![]() $V_{\alpha }$
. However, this quasiconformal map still does not satisfy our requirement to remove the aforementioned discontinuity. To proceed, we need to change
$V_{\alpha }$
. However, this quasiconformal map still does not satisfy our requirement to remove the aforementioned discontinuity. To proceed, we need to change
![]() $\phi _{1}$
or
$\phi _{1}$
or
![]() $\phi _{2}$
further. We will change
$\phi _{2}$
further. We will change
![]() $\phi _{1}$
in what follows.
$\phi _{1}$
in what follows.
To this end, we first define suitable inverse branches of
![]() $\wp $
. Note that
$\wp $
. Note that
![]() $\wp (\tilde {\beta }_{i})=\gamma $
. Let
$\wp (\tilde {\beta }_{i})=\gamma $
. Let
![]() $\psi _{i}$
denote an inverse branch of
$\psi _{i}$
denote an inverse branch of
![]() $\wp $
from
$\wp $
from
![]() $\gamma $
into
$\gamma $
into
![]() $\tilde {\beta }_{i}$
, for
$\tilde {\beta }_{i}$
, for
![]() $i=1,2$
. Recall that
$i=1,2$
. Recall that
![]() $p: \operatorname {\mathbb C}_{2\pi } \mapsto \operatorname {\mathbb C} \setminus \Gamma $
, where
$p: \operatorname {\mathbb C}_{2\pi } \mapsto \operatorname {\mathbb C} \setminus \Gamma $
, where
![]() $p(z) = z^{1/\mu }$
. Put
$p(z) = z^{1/\mu }$
. Put
![]() $\tilde {p}(z) = p(z^{2\pi /\alpha })$
, which maps
$\tilde {p}(z) = p(z^{2\pi /\alpha })$
, which maps
![]() $\operatorname {\mathbb C}_{\alpha }$
onto
$\operatorname {\mathbb C}_{\alpha }$
onto
![]() $\operatorname {\mathbb C} \setminus \Gamma $
. We can extend
$\operatorname {\mathbb C} \setminus \Gamma $
. We can extend
![]() $\tilde {p}$
to its boundary continuously. Moreover, from the definition of
$\tilde {p}$
to its boundary continuously. Moreover, from the definition of
![]() $\mu $
, we have that
$\mu $
, we have that
![]() $x\in \mathbb {R}$
and
$x\in \mathbb {R}$
and
![]() $\tau x \in \ell = \{ z: \arg (z) = \arg (\tau ) \}$
are both mapped by
$\tau x \in \ell = \{ z: \arg (z) = \arg (\tau ) \}$
are both mapped by
![]() $\tilde {p}$
onto the same point in
$\tilde {p}$
onto the same point in
![]() $\Gamma $
. So, in a sense, the ‘transition function’
$\Gamma $
. So, in a sense, the ‘transition function’
![]() $t(x) = \tau x$
, for
$t(x) = \tau x$
, for
![]() $x \in \mathbb {R}$
, identifies points on the lines bounding
$x \in \mathbb {R}$
, identifies points on the lines bounding
![]() $\operatorname {\mathbb C}_{\alpha }$
which correspond to the same origin in
$\operatorname {\mathbb C}_{\alpha }$
which correspond to the same origin in
![]() $\Gamma $
. Now the desired ‘correction function’ is defined as
$\Gamma $
. Now the desired ‘correction function’ is defined as
 $$ \begin{align*} \begin{aligned} \kappa:\, \mathbb{R} &\longrightarrow\mathbb{R},\\ x&\longrightarrow \phi_{1}^{-1}\circ\psi_{1}\circ\wp\circ\phi_{2}(\tau x). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \kappa:\, \mathbb{R} &\longrightarrow\mathbb{R},\\ x&\longrightarrow \phi_{1}^{-1}\circ\psi_{1}\circ\wp\circ\phi_{2}(\tau x). \end{aligned} \end{align*} $$
Since
![]() $\tau x \in \ell $
, the above function
$\tau x \in \ell $
, the above function
![]() $\kappa $
is well defined. Roughly speaking, the function
$\kappa $
is well defined. Roughly speaking, the function
![]() $\kappa $
fixes the difference between
$\kappa $
fixes the difference between
![]() $\phi _{1}$
and
$\phi _{1}$
and
![]() $\phi _{2}$
. With this function, we can now remove the discontinuity by considering a linear interpolation between
$\phi _{2}$
. With this function, we can now remove the discontinuity by considering a linear interpolation between
![]() $\kappa $
on the real axis and the identity on the horizontal line
$\kappa $
on the real axis and the identity on the horizontal line
![]() $\ell _{2}$
. More precisely, we define
$\ell _{2}$
. More precisely, we define
 $$ \begin{align*} \xi_{1}(x+iy)=\bigg(1-\frac{y}{b}\bigg)\kappa(x)+\frac{y}{b}\,x+iy \quad\text{for }0\leq y\leq b. \end{align*} $$
$$ \begin{align*} \xi_{1}(x+iy)=\bigg(1-\frac{y}{b}\bigg)\kappa(x)+\frac{y}{b}\,x+iy \quad\text{for }0\leq y\leq b. \end{align*} $$
This map is quasiconformal, as one can check that the Jacobian of
![]() $\xi $
is non-zero almost everywhere. Moreover, we define
$\xi $
is non-zero almost everywhere. Moreover, we define
In this way, we have just constructed a quasiconformal map of the upper half-plane by setting
 $$ \begin{align*} \begin{aligned} \xi: \mathbb{H}^{+} &\longrightarrow \mathbb{H}^{+},\quad z\longmapsto \begin{cases} ~\xi_{1}(z)&\text{if } 0\leq\operatorname{Im}(z)\leq b,\\ ~\xi_{2}(z)&\text{if } \operatorname{Im}(z)\geq b. \end{cases} \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \xi: \mathbb{H}^{+} &\longrightarrow \mathbb{H}^{+},\quad z\longmapsto \begin{cases} ~\xi_{1}(z)&\text{if } 0\leq\operatorname{Im}(z)\leq b,\\ ~\xi_{2}(z)&\text{if } \operatorname{Im}(z)\geq b. \end{cases} \end{aligned} \end{align*} $$
We still need to define a map on the parallelogram Q. Denote by
![]() $I_{1}$
the side of Q on the real axis (that is,
$I_{1}$
the side of Q on the real axis (that is,
![]() $I_{1}=[0,d]$
), and by
$I_{1}=[0,d]$
), and by
![]() $I_{2}$
the side on the line
$I_{2}$
the side on the line
![]() $\ell $
(that is,
$\ell $
(that is,
![]() $I_{2}=\{re^{i\alpha }: 0\leq r\leq b/\sin (\alpha )\}$
). The other two sides of Q are denoted by
$I_{2}=\{re^{i\alpha }: 0\leq r\leq b/\sin (\alpha )\}$
). The other two sides of Q are denoted by
![]() $I_{3}$
, which is parallel to
$I_{3}$
, which is parallel to
![]() $I_{1}$
, and
$I_{1}$
, and
![]() $I_{4}$
, which is parallel to
$I_{4}$
, which is parallel to
![]() $I_{2}$
. We put
$I_{2}$
. We put
![]() $\hat {I}_{1}=\xi (I_{1})$
,
$\hat {I}_{1}=\xi (I_{1})$
,
![]() $\hat {I}_{2}=I_{2}$
,
$\hat {I}_{2}=I_{2}$
,
![]() $\hat {I}_{3}=I_{3}$
and
$\hat {I}_{3}=I_{3}$
and
![]() $\hat {I}_{4}=\xi (I_{4})$
. Then the
$\hat {I}_{4}=\xi (I_{4})$
. Then the
![]() $\hat {I}_{i}$
,
$\hat {I}_{i}$
,
![]() $i=1,\ldots ,4$
, form a quadrilateral, denoted by
$i=1,\ldots ,4$
, form a quadrilateral, denoted by
![]() $\hat {Q}$
. We continue to define a new quadrilateral
$\hat {Q}$
. We continue to define a new quadrilateral
![]() $\tilde {Q}$
formed by the
$\tilde {Q}$
formed by the
![]() $\tilde {I}_{i}$
,
$\tilde {I}_{i}$
,
![]() $i=1,\ldots ,4$
, where
$i=1,\ldots ,4$
, where
and
Now we can define a boundary map between Q and
![]() $\tilde {Q}$
by using
$\tilde {Q}$
by using
![]() $\phi _{1}\circ \xi $
on
$\phi _{1}\circ \xi $
on
![]() $I_{1}\cup I_{4}$
and
$I_{1}\cup I_{4}$
and
![]() $\phi _{2}\circ \xi $
on
$\phi _{2}\circ \xi $
on
![]() $I_{2}\cup I_{3}$
. The boundary map extends to the interior of Q quasiconformally; see [Reference Branner and FagellaBF14, Lemma 2.24]. So we have a quasiconformal map
$I_{2}\cup I_{3}$
. The boundary map extends to the interior of Q quasiconformally; see [Reference Branner and FagellaBF14, Lemma 2.24]. So we have a quasiconformal map
We can now define our promised map
 $$ \begin{align*} \Phi :~ \operatorname{\mathbb C}_{\alpha}\,&\longrightarrow\, V,~\,~ z\longmapsto \begin{cases} ~\phi_{1}(\xi(z)) &\text{if }z\in S\setminus Q,\\ ~\phi_{2}(z) &\text{if }z\in \widehat{S}\setminus Q,\\ ~h(z) &\text{if }z\in Q,\\ ~z &\text{if }z\in V_{\alpha}. \end{cases} \end{align*} $$
$$ \begin{align*} \Phi :~ \operatorname{\mathbb C}_{\alpha}\,&\longrightarrow\, V,~\,~ z\longmapsto \begin{cases} ~\phi_{1}(\xi(z)) &\text{if }z\in S\setminus Q,\\ ~\phi_{2}(z) &\text{if }z\in \widehat{S}\setminus Q,\\ ~h(z) &\text{if }z\in Q,\\ ~z &\text{if }z\in V_{\alpha}. \end{cases} \end{align*} $$
One can then check that the map
extends continuously across the logarithmic spiral
![]() $\Gamma $
and thus gives us, by construction, a quasimeromorphic function of the plane.
$\Gamma $
and thus gives us, by construction, a quasimeromorphic function of the plane.
So by the measurable Riemann mapping theorem (cf. [Reference AhlforsAhl06]) there exist a quasiconformal homeomorphism
![]() $\Psi $
and a meromorphic function f such that
$\Psi $
and a meromorphic function f such that
![]() $G=f\circ \Psi $
. By our construction, G is quasiconformal only in
$G=f\circ \Psi $
. By our construction, G is quasiconformal only in
![]() $(h\circ q)^{-1}(W)$
, where
$(h\circ q)^{-1}(W)$
, where
![]() $W=\operatorname {\mathbb C}_{\alpha }\setminus V_{\alpha }$
.
$W=\operatorname {\mathbb C}_{\alpha }\setminus V_{\alpha }$
.
It follows from our construction that f has exactly four critical values and no asymptotic values. In other words,
![]() $f\in \operatorname {\mathcal {S}}_{4}$
. Moreover, f has only double poles.
$f\in \operatorname {\mathcal {S}}_{4}$
. Moreover, f has only double poles.
To derive some asymptotic properties of f, we will need the well-known Teichmüller–Wittich–Belinskii theorem concerning conformality of a quasiconformal mapping at a point. We refer to [Reference AhlforsAhl06, Reference Lehto and VirtanenLV73] for background on quasiconformal mappings and also for this result. For our purpose, a stronger result is required. We first recall some relevant notions. Let
![]() $\varphi :\operatorname {\mathbb C}\to \operatorname {\mathbb C}$
be a quasiconformal mapping. Then the dilatation of
$\varphi :\operatorname {\mathbb C}\to \operatorname {\mathbb C}$
be a quasiconformal mapping. Then the dilatation of
![]() $\varphi $
at a point z is
$\varphi $
at a point z is
 $$ \begin{align*}K_{\varphi}(z):=\frac{|\varphi_{z}|+|\varphi_{\bar{z}}|}{|\varphi_{z}|-|\varphi_{\bar{z}}|}=\frac{1+|\mu_{\varphi}|}{1-|\mu_{\varphi}|},\end{align*} $$
$$ \begin{align*}K_{\varphi}(z):=\frac{|\varphi_{z}|+|\varphi_{\bar{z}}|}{|\varphi_{z}|-|\varphi_{\bar{z}}|}=\frac{1+|\mu_{\varphi}|}{1-|\mu_{\varphi}|},\end{align*} $$
where
![]() $\mu _{\varphi }:=\varphi _{\bar {z}}/\varphi _{z}$
is the complex dilatation of
$\mu _{\varphi }:=\varphi _{\bar {z}}/\varphi _{z}$
is the complex dilatation of
![]() $\varphi $
.
$\varphi $
.
The above-mentioned result is stated as follows; see [Reference Aspenberg and CuiAC21, Lemma 2.2].
Proposition 3.2. Let
![]() $\varphi :\operatorname {\mathbb C}\to \operatorname {\mathbb C}$
be quasiconformal. Put
$\varphi :\operatorname {\mathbb C}\to \operatorname {\mathbb C}$
be quasiconformal. Put
![]() $A=\{z\in \operatorname {\mathbb C}:\mu _{\varphi }\neq 0\}$
. If
$A=\{z\in \operatorname {\mathbb C}:\mu _{\varphi }\neq 0\}$
. If
 $\iint _{A\setminus \operatorname {\mathbb D}} dx\,dy/(x^{2}+y^{2})<\infty $
, then
$\iint _{A\setminus \operatorname {\mathbb D}} dx\,dy/(x^{2}+y^{2})<\infty $
, then
![]() $\varphi (z)\sim z$
as
$\varphi (z)\sim z$
as
![]() $z\to \infty $
. Upon normalization, one has
$z\to \infty $
. Upon normalization, one has
![]() $\varphi (z)=z+o(z)$
as
$\varphi (z)=z+o(z)$
as
![]() $z\to \infty $
.
$z\to \infty $
.
Note that W is the union of two half-strips, which means that the set
![]() $W\setminus \operatorname {\mathbb D}$
has finite logarithmic area, that is, the integration above holds. So
$W\setminus \operatorname {\mathbb D}$
has finite logarithmic area, that is, the integration above holds. So
![]() $\Psi $
satisfies the conditions in Proposition 3.2. So we have, up to normalization,
$\Psi $
satisfies the conditions in Proposition 3.2. So we have, up to normalization,
3.1. Distribution of poles of G
Now fix
![]() $R>0$
large. We will be interested in counting the number of poles in the closed disk
$R>0$
large. We will be interested in counting the number of poles in the closed disk
![]() $\overline {D}(0,R)$
. This will follow from the following area formula for a domain bounded by two logarithmic spirals. More precisely, let
$\overline {D}(0,R)$
. This will follow from the following area formula for a domain bounded by two logarithmic spirals. More precisely, let
![]() $\sigma $
be a (non-zero) complex number and
$\sigma $
be a (non-zero) complex number and
![]() $R>0$
. Put
$R>0$
. Put
![]() $\psi (z)=z^{\sigma }$
for
$\psi (z)=z^{\sigma }$
for
![]() $z\in \operatorname {\mathbb C}_{2\pi }$
with chosen principle branch. Let
$z\in \operatorname {\mathbb C}_{2\pi }$
with chosen principle branch. Let
![]() $\Gamma _{\beta }$
and
$\Gamma _{\beta }$
and
![]() $\Gamma _{\gamma }$
be the
$\Gamma _{\gamma }$
be the
![]() $\psi $
-images of two radial lines of arguments
$\psi $
-images of two radial lines of arguments
![]() $\beta $
and
$\beta $
and
![]() $\gamma $
respectively, where
$\gamma $
respectively, where
![]() $0\leq \beta <\gamma \leq 2\pi $
. See Figure 5. Denote by
$0\leq \beta <\gamma \leq 2\pi $
. See Figure 5. Denote by
![]() $A:=A_{\gamma -\beta }$
the bounded region bounded by
$A:=A_{\gamma -\beta }$
the bounded region bounded by
![]() $\Gamma _{\beta }$
,
$\Gamma _{\beta }$
,
![]() $\Gamma _{\gamma }$
and the circle
$\Gamma _{\gamma }$
and the circle
![]() $\{z:|z|=R\}$
, and by
$\{z:|z|=R\}$
, and by
![]() $B:=B_{\gamma -\beta }$
the preimage of A under
$B:=B_{\gamma -\beta }$
the preimage of A under
![]() $\psi $
. Then we have the following formula for the (Euclidean) area of A and B.
$\psi $
. Then we have the following formula for the (Euclidean) area of A and B.

Figure 5 The area of the domain A bounded by two logarithmic spirals can be computed by using a logarithmic change of variable.
Proposition 3.3.
 $$ \begin{align*} \operatorname{area} A&=\frac{(\gamma-\beta)|\sigma|^{2}}{2\operatorname{Re} \sigma}R^{2};\\[1pt] \operatorname{area} B&=\frac{\operatorname{Re} \sigma}{4\operatorname{Im}\sigma}(e^{2\gamma({\operatorname{Im}\sigma}/{\operatorname{Re}\sigma})} -e^{2\beta({\operatorname{Im}\sigma}/{\operatorname{Re}\sigma})})\cdot R^{{2}/{\operatorname{Re}(\sigma)}}. \end{align*} $$
$$ \begin{align*} \operatorname{area} A&=\frac{(\gamma-\beta)|\sigma|^{2}}{2\operatorname{Re} \sigma}R^{2};\\[1pt] \operatorname{area} B&=\frac{\operatorname{Re} \sigma}{4\operatorname{Im}\sigma}(e^{2\gamma({\operatorname{Im}\sigma}/{\operatorname{Re}\sigma})} -e^{2\beta({\operatorname{Im}\sigma}/{\operatorname{Re}\sigma})})\cdot R^{{2}/{\operatorname{Re}(\sigma)}}. \end{align*} $$
Proof. Let C be the shaded domain in Figure 5, which is mapped by the exponential map to A. Then
 $$ \begin{align*}\operatorname{area} A&=\iint_{C}|(e^{z})^{\prime}|^{2}|\,dz|^{2}\\[3pt] &=\int_{-\infty}^{\log R}e^{2x}\int_{({\beta-x\operatorname{Im}(1/\sigma)})/{\operatorname{Re}(1/\sigma)}}^{({\gamma-x\operatorname{Im}(1/\sigma)})/{\operatorname{Re}(1/\sigma)}}\,dy\,dx=\frac{(\gamma-\beta)|\sigma|^{2}}{2\operatorname{Re} \sigma}R^{2}.\end{align*} $$
$$ \begin{align*}\operatorname{area} A&=\iint_{C}|(e^{z})^{\prime}|^{2}|\,dz|^{2}\\[3pt] &=\int_{-\infty}^{\log R}e^{2x}\int_{({\beta-x\operatorname{Im}(1/\sigma)})/{\operatorname{Re}(1/\sigma)}}^{({\gamma-x\operatorname{Im}(1/\sigma)})/{\operatorname{Re}(1/\sigma)}}\,dy\,dx=\frac{(\gamma-\beta)|\sigma|^{2}}{2\operatorname{Re} \sigma}R^{2}.\end{align*} $$
Similarly, by using the map
![]() $e^{z/\sigma }$
we can obtain the area formula for B. We omit the details here.
$e^{z/\sigma }$
we can obtain the area formula for B. We omit the details here.
We will also use in what follows some standard notions and notation from Nevanlinna theory [Reference Goldberg and OstrovskiiGO08, Reference HaymanHay64, Reference NevanlinnaNev70]. In particular,
![]() $n(r,f)$
denotes the number of poles of f in the disk
$n(r,f)$
denotes the number of poles of f in the disk
![]() $\overline {D}(0,r)$
,
$\overline {D}(0,r)$
,
![]() $m(r,f)$
the proximity function and
$m(r,f)$
the proximity function and
![]() $T(r,f)$
is the Nevanlinna characteristic of f. The order of a meromorphic function f is defined by
$T(r,f)$
is the Nevanlinna characteristic of f. The order of a meromorphic function f is defined by
 $$ \begin{align*}\rho(f)=\limsup_{r\to\infty}\frac{\log T(r,f)}{\log r}.\end{align*} $$
$$ \begin{align*}\rho(f)=\limsup_{r\to\infty}\frac{\log T(r,f)}{\log r}.\end{align*} $$
By using Proposition 3.3, we have the following estimate.
Proposition 3.4.
 $$\begin{align} n(r,f)=\mathcal{O}(r^{({\alpha^{2}+(\log|\tau|)^{2}})/{\pi\alpha}}) , \end{align} $$
$$\begin{align} n(r,f)=\mathcal{O}(r^{({\alpha^{2}+(\log|\tau|)^{2}})/{\pi\alpha}}) , \end{align} $$
 $$\begin{align} \rho(f)=\frac{\alpha^{2}+(\log|\tau|)^{2}}{\pi\alpha}. \end{align} $$
$$\begin{align} \rho(f)=\frac{\alpha^{2}+(\log|\tau|)^{2}}{\pi\alpha}. \end{align} $$
Proof. To estimate the number of poles of f in a certain disk, by (3.3) it suffices to estimate the poles for the map G for a sufficiently large disk. This can be obtained by comparing the area of the disk and the area of a preimage of a parallelogram for the Weierstrass elliptic function under the spiral function
![]() $h \circ q(z) = z^{\eta }$
, where
$h \circ q(z) = z^{\eta }$
, where
![]() $\eta = \mu \alpha /2\pi $
. Then it follows from Proposition 3.3 that
$\eta = \mu \alpha /2\pi $
. Then it follows from Proposition 3.3 that
 $$ \begin{align*}n(r,G)\sim C\,r^{{\alpha^{2}+(\log|\tau|)^{2}}/{\pi\alpha}},\end{align*} $$
$$ \begin{align*}n(r,G)\sim C\,r^{{\alpha^{2}+(\log|\tau|)^{2}}/{\pi\alpha}},\end{align*} $$
for large r and for some positive constant C. This gives (3.4a ).
To obtain (3.4b
), we need a result of Teichmüller [Reference TeichmüllerTei37] which states that for a meromorphic function
![]() $f\in \operatorname {\mathcal {S}}$
, if
$f\in \operatorname {\mathcal {S}}$
, if
![]() $\infty $
is not an asymptotic value and the multiplicities of poles are bounded, then
$\infty $
is not an asymptotic value and the multiplicities of poles are bounded, then
![]() $m(r,f)$
is bounded. This means that the order of f can be estimated by using the integrated counting function
$m(r,f)$
is bounded. This means that the order of f can be estimated by using the integrated counting function
![]() $N(r,f)$
of f, where
$N(r,f)$
of f, where
![]() $N(r,f)=T(r,f)-m(r,f)$
. Then classical results on the comparison on the growth scale of
$N(r,f)=T(r,f)-m(r,f)$
. Then classical results on the comparison on the growth scale of
![]() $N(r,f)$
and
$N(r,f)$
and
![]() $n(r,f)$
show that
$n(r,f)$
show that
 $$ \begin{align*}\rho(f)=\limsup_{r\to\infty}\frac{\log n(r,f)}{\log r}.\end{align*} $$
$$ \begin{align*}\rho(f)=\limsup_{r\to\infty}\frac{\log n(r,f)}{\log r}.\end{align*} $$
Now (3.4b
) follows from our estimate of
![]() $n(r,f)$
.
$n(r,f)$
.
In the above constructions, we have from the beginning fixed the parameters
![]() $\alpha $
and
$\alpha $
and
![]() $\tau $
. If we now vary these parameters, we can achieve every finite order. To be more specific, we have the following proposition.
$\tau $
. If we now vary these parameters, we can achieve every finite order. To be more specific, we have the following proposition.
Proposition 3.5. For any given
![]() $\rho \in (0,\infty )$
, there exist
$\rho \in (0,\infty )$
, there exist
![]() $\alpha \in (0,2\pi ]$
and
$\alpha \in (0,2\pi ]$
and
![]() $\tau $
satisfying (3.1) such that
$\tau $
satisfying (3.1) such that
 $$ \begin{align} \rho=\frac{\alpha^{2}+(\log|\tau|)^{2}}{\pi\alpha}. \end{align} $$
$$ \begin{align} \rho=\frac{\alpha^{2}+(\log|\tau|)^{2}}{\pi\alpha}. \end{align} $$
Moreover, there is a meromorphic function
![]() $f\in \operatorname {\mathcal {S}}_{4}$
such that
$f\in \operatorname {\mathcal {S}}_{4}$
such that
![]() $\rho (f)=\rho $
.
$\rho (f)=\rho $
.
We now put
 $$ \begin{align} \eta=\frac{\alpha\mu}{2\pi}=\frac{1}{2\pi}(\alpha-i\log|\tau|). \end{align} $$
$$ \begin{align} \eta=\frac{\alpha\mu}{2\pi}=\frac{1}{2\pi}(\alpha-i\log|\tau|). \end{align} $$
Later on we will also need to estimate
![]() $|a^{\eta }|$
in terms of the modulus of a. Note that
$|a^{\eta }|$
in terms of the modulus of a. Note that
![]() $\eta $
defined above is a complex number. We first prove the following result. For simplicity, we also use
$\eta $
defined above is a complex number. We first prove the following result. For simplicity, we also use
![]() $\rho $
as given in (3.5).
$\rho $
as given in (3.5).
Proposition 3.6. For
![]() $a\in \operatorname {\mathbb C}$
, we have
$a\in \operatorname {\mathbb C}$
, we have
Proof. Let S be the standard strip
![]() $S = \{ z= x + i y : 0 < y < 2\pi \}$
and put
$S = \{ z= x + i y : 0 < y < 2\pi \}$
and put
![]() $P = (1/\mu ) S = \{ z : \mu z \in S \}$
. First, recall that
$P = (1/\mu ) S = \{ z : \mu z \in S \}$
. First, recall that
![]() $\exp $
maps the oblique strip P onto
$\exp $
maps the oblique strip P onto
![]() $\operatorname {\mathbb C} \setminus \Gamma $
. It has a continuous extension to the boundary, by the definition of
$\operatorname {\mathbb C} \setminus \Gamma $
. It has a continuous extension to the boundary, by the definition of
![]() $\mu = 1-i \kappa $
(whose real part is equal to
$\mu = 1-i \kappa $
(whose real part is equal to
![]() $1$
). Here
$1$
). Here
![]() $\kappa =(\log |\tau |)/\alpha $
. To make it injective, let us extend
$\kappa =(\log |\tau |)/\alpha $
. To make it injective, let us extend
![]() $\exp $
only to the lower boundary of the strip P, so that, for instance, the preimage of
$\exp $
only to the lower boundary of the strip P, so that, for instance, the preimage of
![]() $z=1$
under exp has its preimage at the origin, that is, the argument of this preimage is
$z=1$
under exp has its preimage at the origin, that is, the argument of this preimage is
![]() $0$
. Then the argument of an arbitrary complex number
$0$
. Then the argument of an arbitrary complex number
![]() $a \in \mathbb {C}$
is the imaginary part of the ‘spiral branch’
$a \in \mathbb {C}$
is the imaginary part of the ‘spiral branch’
![]() $\log _{P}(a)$
of a; that is,
$\log _{P}(a)$
of a; that is,
![]() $\log _{p}$
is this particular inverse of
$\log _{p}$
is this particular inverse of
![]() $\exp $
mapping
$\exp $
mapping
![]() $\operatorname {\mathbb C} \setminus \Gamma $
onto P.
$\operatorname {\mathbb C} \setminus \Gamma $
onto P.
By definition
![]() $a^{\mu } = e^{\mu \log a} = e^{(1-i\kappa ) (\ln r + i \theta (r))}$
, where
$a^{\mu } = e^{\mu \log a} = e^{(1-i\kappa ) (\ln r + i \theta (r))}$
, where
![]() $\theta =\theta (r)$
now depends on
$\theta =\theta (r)$
now depends on
![]() $r:=|a|$
in such a way that, if
$r:=|a|$
in such a way that, if
![]() $\tilde {\theta } \in [0,2\pi )$
is the natural argument for a, then
$\tilde {\theta } \in [0,2\pi )$
is the natural argument for a, then
![]() $\theta (r) = \tilde {\theta } + 2\pi k $
, where k is the unique integer such that
$\theta (r) = \tilde {\theta } + 2\pi k $
, where k is the unique integer such that
Hence there is some
![]() $\delta \in [0,2\pi )$
such that
$\delta \in [0,2\pi )$
such that
 $$ \begin{align*} k = \frac{\kappa \log r - \tilde{\theta} + \delta}{2\pi}. \end{align*} $$
$$ \begin{align*} k = \frac{\kappa \log r - \tilde{\theta} + \delta}{2\pi}. \end{align*} $$
Replacing the expression for k in
![]() $\theta (r)$
, and with
$\theta (r)$
, and with
![]() $\kappa = (\log |\tau |)/\alpha $
, we have
$\kappa = (\log |\tau |)/\alpha $
, we have
 $$ \begin{align*} |a^{\eta}|= |a^{\mu \alpha/2\pi}| = r^{\alpha/2\pi} e^{\theta(r) \log|\tau|/2\pi} = r^{({\alpha^{2} + (\log|\tau|)^{2}})/{2\pi \alpha}} e^{{\delta \log |\tau|}/{2 \pi}}.\\[-38pt] \end{align*} $$
$$ \begin{align*} |a^{\eta}|= |a^{\mu \alpha/2\pi}| = r^{\alpha/2\pi} e^{\theta(r) \log|\tau|/2\pi} = r^{({\alpha^{2} + (\log|\tau|)^{2}})/{2\pi \alpha}} e^{{\delta \log |\tau|}/{2 \pi}}.\\[-38pt] \end{align*} $$
The strategy below follows in a similar way to [Reference Aspenberg and CuiAC21, §3]. We first estimate asymptotic behaviours of the constructed function f near its poles, which will be useful in estimating the Hausdorff dimension of escaping sets later on. Then we show that by varying parameters
![]() $\alpha $
and
$\alpha $
and
![]() $\tau $
we obtain functions in
$\tau $
we obtain functions in
![]() $\operatorname {\mathcal {S}}_{4}$
which are actually equivalent. This is crucial for completing the proof of Theorem 1.2.
$\operatorname {\mathcal {S}}_{4}$
which are actually equivalent. This is crucial for completing the proof of Theorem 1.2.
3.2. Local behaviours near poles
We first consider the local behaviours of the quasimeromorphic map G near its poles. In the following,
![]() $A\sim B$
means that A and B have comparable modulus. Let
$A\sim B$
means that A and B have comparable modulus. Let
![]() $z_{0}$
be a pole of G. By (3.2),
$z_{0}$
be a pole of G. By (3.2),
![]() $\Phi (h(q(z_{0})))$
is a pole of the function
$\Phi (h(q(z_{0})))$
is a pole of the function
![]() $\wp $
. Put
$\wp $
. Put
![]() $\zeta =\Phi (h(q(z)))$
and
$\zeta =\Phi (h(q(z)))$
and
![]() $\zeta _{0}=\Phi (h(q(z_{0})))$
. Since
$\zeta _{0}=\Phi (h(q(z_{0})))$
. Since
![]() $\zeta _{0}$
is a pole of
$\zeta _{0}$
is a pole of
![]() $\wp $
, we see that there exists a constant C such that
$\wp $
, we see that there exists a constant C such that
 $$ \begin{align} \wp(\zeta)\sim\bigg(\frac{C}{\zeta-\zeta_{0}}\bigg)^{2}\quad\text{as } \zeta\to\zeta_{0}. \end{align} $$
$$ \begin{align} \wp(\zeta)\sim\bigg(\frac{C}{\zeta-\zeta_{0}}\bigg)^{2}\quad\text{as } \zeta\to\zeta_{0}. \end{align} $$
By the construction of
![]() $\Phi $
, we have that
$\Phi $
, we have that
 $$ \begin{align*}\zeta-\zeta_{0}\sim C^{\prime}( h(q(z))-h(q(z_{0})))=C^{\prime}( z^{\alpha\mu/(2\pi)}-z_{0}^{\alpha\mu/(2\pi)} )\quad\text{as } z\to z_{0},\end{align*} $$
$$ \begin{align*}\zeta-\zeta_{0}\sim C^{\prime}( h(q(z))-h(q(z_{0})))=C^{\prime}( z^{\alpha\mu/(2\pi)}-z_{0}^{\alpha\mu/(2\pi)} )\quad\text{as } z\to z_{0},\end{align*} $$
where
![]() $C^{\prime }$
is some constant. This, together with (3.2) and (3.7), shows that
$C^{\prime }$
is some constant. This, together with (3.2) and (3.7), shows that
 $$ \begin{align} G(z)\sim\bigg(\frac{C^{\prime\prime}}{z^{\alpha\mu/(2\pi)}-z_{0}^{\alpha\mu/(2\pi)}}\bigg)^{2}\quad\text{as } z\to z_{0}, \end{align} $$
$$ \begin{align} G(z)\sim\bigg(\frac{C^{\prime\prime}}{z^{\alpha\mu/(2\pi)}-z_{0}^{\alpha\mu/(2\pi)}}\bigg)^{2}\quad\text{as } z\to z_{0}, \end{align} $$
where
![]() $C^{\prime \prime }$
depends only on C and
$C^{\prime \prime }$
depends only on C and
![]() $C^{\prime }$
. Note that
$C^{\prime }$
. Note that
![]() $z_{0}$
is a double pole of G. We may thus assume that
$z_{0}$
is a double pole of G. We may thus assume that
 $$ \begin{align} G(z)\sim\bigg(\frac{a(z)}{z-z_{0}}\bigg)^{2}\quad\text{as } z\to z_{0} \end{align} $$
$$ \begin{align} G(z)\sim\bigg(\frac{a(z)}{z-z_{0}}\bigg)^{2}\quad\text{as } z\to z_{0} \end{align} $$
for some function a which is holomorphic near in some neighbourhood of
![]() $z_{0}$
and, moreover,
$z_{0}$
and, moreover,
![]() $a(z_{0})\neq 0$
. By comparing (3.8) and (3.9), we see that
$a(z_{0})\neq 0$
. By comparing (3.8) and (3.9), we see that
 $$ \begin{align*}a(z)\sim C^{\prime\prime}\frac{z-z_{0}}{z^{\alpha\mu/(2\pi)}-z_{0}^{\alpha\mu/(2\pi)}}\quad\text{as } z\to z_{0}.\end{align*} $$
$$ \begin{align*}a(z)\sim C^{\prime\prime}\frac{z-z_{0}}{z^{\alpha\mu/(2\pi)}-z_{0}^{\alpha\mu/(2\pi)}}\quad\text{as } z\to z_{0}.\end{align*} $$
Recall that
![]() $\eta $
is defined in (3.6). By taking limit and using L’Hospital’s rule, we obtain
$\eta $
is defined in (3.6). By taking limit and using L’Hospital’s rule, we obtain
 $$ \begin{align*}a(z_{0})\sim C^{\prime\prime\prime} z_{0}^{1-\alpha\mu/(2\pi)}=C^{\prime\prime\prime} z_{0}^{1-\eta}.\end{align*} $$
$$ \begin{align*}a(z_{0})\sim C^{\prime\prime\prime} z_{0}^{1-\alpha\mu/(2\pi)}=C^{\prime\prime\prime} z_{0}^{1-\eta}.\end{align*} $$
Denote
![]() $w=\Phi (z)$
and
$w=\Phi (z)$
and
![]() $w_{0}=\Phi (z_{0})$
. Then
$w_{0}=\Phi (z_{0})$
. Then
![]() $w_{0}$
is a double pole of f. Assume that
$w_{0}$
is a double pole of f. Assume that
 $$ \begin{align*}f(w)\sim\bigg( \frac{b(w)}{w-w_{0}} \bigg)^{2}\quad\text{as } w\to w_{0}.\end{align*} $$
$$ \begin{align*}f(w)\sim\bigg( \frac{b(w)}{w-w_{0}} \bigg)^{2}\quad\text{as } w\to w_{0}.\end{align*} $$
Here
![]() $b(w)$
is a function holomorphic in
$b(w)$
is a function holomorphic in
![]() $w_{0}$
and
$w_{0}$
and
![]() $b(w_{0})\neq 0$
. So with (3.9) we see that
$b(w_{0})\neq 0$
. So with (3.9) we see that
 $$ \begin{align*}b(w)\sim a(z)\frac{w-w_{0}}{z-z_{0}}\end{align*} $$
$$ \begin{align*}b(w)\sim a(z)\frac{w-w_{0}}{z-z_{0}}\end{align*} $$
as
![]() $z\to z_{0}$
. Note that (3.3) implies that
$z\to z_{0}$
. Note that (3.3) implies that
![]() $w\to w_{0}$
as
$w\to w_{0}$
as
![]() $z\to z_{0}$
. Again, (3.3) will also imply that
$z\to z_{0}$
. Again, (3.3) will also imply that
 $$ \begin{align*}b(w_{0})\sim a(z_{0})\lim_{z\to z_{0}}\frac{w-w_{0}}{z-z_{0}}=a(z_{0}).\end{align*} $$
$$ \begin{align*}b(w_{0})\sim a(z_{0})\lim_{z\to z_{0}}\frac{w-w_{0}}{z-z_{0}}=a(z_{0}).\end{align*} $$
It follows that near a pole
![]() $w_{0}$
of f, we have the following asymptotic relation:
$w_{0}$
of f, we have the following asymptotic relation:
 $$ \begin{align} f(w)=\bigg( \frac{C_{1} w_{0}^{1-\eta}}{w-w_{0}} \bigg)^{2}\quad\text{as } w\to w_{0}, \end{align} $$
$$ \begin{align} f(w)=\bigg( \frac{C_{1} w_{0}^{1-\eta}}{w-w_{0}} \bigg)^{2}\quad\text{as } w\to w_{0}, \end{align} $$
where
![]() $C_{1}$
is some constant.
$C_{1}$
is some constant.
3.3. Equivalence
By choosing distinct parameters
![]() $(\alpha _{i},\tau _{i})$
we may obtain that the
$(\alpha _{i},\tau _{i})$
we may obtain that the
![]() $\rho _{i}$
as defined in (3.4b
) are different for
$\rho _{i}$
as defined in (3.4b
) are different for
![]() $i=1,2$
. So by the construction we can have two functions
$i=1,2$
. So by the construction we can have two functions
![]() $f_{i}\in \operatorname {\mathcal {S}}_{4}$
whose orders are
$f_{i}\in \operatorname {\mathcal {S}}_{4}$
whose orders are
![]() $\rho _{i}$
. Following the idea of proof given in [Reference Aspenberg and CuiAC21, Theorem 3.2], we see that
$\rho _{i}$
. Following the idea of proof given in [Reference Aspenberg and CuiAC21, Theorem 3.2], we see that
![]() $f_{1}$
is quasiconformally equivalent to
$f_{1}$
is quasiconformally equivalent to
![]() $f_{2}$
. We omit this proof here, merely stating the result below. We leave the details to the interested reader.
$f_{2}$
. We omit this proof here, merely stating the result below. We leave the details to the interested reader.
Proposition 3.7.
![]() $f_{1}$
is quasiconformally equivalent to
$f_{1}$
is quasiconformally equivalent to
![]() $f_{2}$
.
$f_{2}$
.
One may notice that the above constructions only give meromorphic functions in
![]() $\operatorname {\mathcal {S}}_{4}$
of finite but non-zero order. To achieve zero or full Hausdorff dimension of escaping sets, we may need functions of zero or infinite order. We mention several examples below which will suffice for our purposes.
$\operatorname {\mathcal {S}}_{4}$
of finite but non-zero order. To achieve zero or full Hausdorff dimension of escaping sets, we may need functions of zero or infinite order. We mention several examples below which will suffice for our purposes.
3.4. Zero order
To have a zero-order meromorphic function in
![]() $\operatorname {\mathcal {S}}_{4}$
, one can consider the one used in [Reference Aspenberg and CuiAC21, §4.1]. Roughly speaking, the function f is obtained by precomposing a suitably chosen Weierstraß elliptic function with an inverse branch of the function
$\operatorname {\mathcal {S}}_{4}$
, one can consider the one used in [Reference Aspenberg and CuiAC21, §4.1]. Roughly speaking, the function f is obtained by precomposing a suitably chosen Weierstraß elliptic function with an inverse branch of the function
![]() $\cosh $
. The obtained function is meromorphic in a certain slit plane. One can then use some basic properties of these two functions to show that it can be extended continuously across the slit and thus gives a meromorphic function in the plane. That this function belongs to
$\cosh $
. The obtained function is meromorphic in a certain slit plane. One can then use some basic properties of these two functions to show that it can be extended continuously across the slit and thus gives a meromorphic function in the plane. That this function belongs to
![]() $\operatorname {\mathcal {S}}_{4}$
is clear since all singular values are just critical values of the Weierstraß elliptic function. It is also clear that f has zero order by checking the counting function of poles, which can be computed explicitly. We omit the details here.
$\operatorname {\mathcal {S}}_{4}$
is clear since all singular values are just critical values of the Weierstraß elliptic function. It is also clear that f has zero order by checking the counting function of poles, which can be computed explicitly. We omit the details here.
3.5. Infinite order
As for infinite-order functions in
![]() $\operatorname {\mathcal {S}}_{4}$
, consider the function
$\operatorname {\mathcal {S}}_{4}$
, consider the function
where
![]() $\wp $
is a Weierstrass elliptic function with two periods
$\wp $
is a Weierstrass elliptic function with two periods
![]() $2\pi $
and
$2\pi $
and
![]() $\tau $
such that
$\tau $
such that
![]() $\tau $
is not a real multiple of
$\tau $
is not a real multiple of
![]() $2\pi $
. It follows by construction that f has four critical values which are exactly the critical values of
$2\pi $
. It follows by construction that f has four critical values which are exactly the critical values of
![]() $\wp $
and has no asymptotic values. That
$\wp $
and has no asymptotic values. That
![]() $\rho (f)=\infty $
follows directly from [Reference Edrei and FuchsEF64, Corollary 1.2]. This can also be obtained by checking the counting functions of poles.
$\rho (f)=\infty $
follows directly from [Reference Edrei and FuchsEF64, Corollary 1.2]. This can also be obtained by checking the counting functions of poles.
4. Estimate of the dimension
We will need to estimate the Hausdorff dimension of the escaping sets for the Speiser functions in
![]() $\operatorname {\mathcal {S}}_{4}$
constructed in the previous section, which then finishes the proof of Theorem 1.1. This will follow from the following estimate.
$\operatorname {\mathcal {S}}_{4}$
constructed in the previous section, which then finishes the proof of Theorem 1.1. This will follow from the following estimate.
Proposition 4.1. Let
![]() $\rho \in [0,\infty )$
. Then there exists a meromorphic function
$\rho \in [0,\infty )$
. Then there exists a meromorphic function
![]() $f\in \operatorname {\mathcal {S}}_{4}$
such that
$f\in \operatorname {\mathcal {S}}_{4}$
such that
![]() $\operatorname {dim}\operatorname {\mathcal {I}}(f)=({2\rho }/({1+\rho })$
.
$\operatorname {dim}\operatorname {\mathcal {I}}(f)=({2\rho }/({1+\rho })$
.
Before we prove this, we state the following direct consequence.
Corollary 4.1. For any
![]() $d\in [0,2)$
, there exists
$d\in [0,2)$
, there exists
![]() $f\in \operatorname {\mathcal {S}}_{4}$
such that
$f\in \operatorname {\mathcal {S}}_{4}$
such that
![]() $\operatorname {dim}\operatorname {\mathcal {I}}(f)=d$
.
$\operatorname {dim}\operatorname {\mathcal {I}}(f)=d$
.
Therefore, Theorem 1.1 is proved except for the case where
![]() $d=2$
, which will be discussed in the final part of this section. By combining this with Proposition 3.7, Theorem 1.2 follows.
$d=2$
, which will be discussed in the final part of this section. By combining this with Proposition 3.7, Theorem 1.2 follows.
The rest of the proof will be devoted to the proof of the above Proposition 4.1. We only give a sketch of the proof, as the estimate of the Hausdorff dimension for escaping sets for our constructed functions will use the same idea as in [Reference Aspenberg and CuiAC21]: the upper bound follows from a result of Bergweiler and Kotus [Reference Bergweiler and KotusBK12], while the lower bound uses the spherical version of a well-known result of McMullen [Reference McMullenMcM87].
Proof of Proposition 4.1
For any given
![]() $\rho \in [0,\infty )$
, there exist
$\rho \in [0,\infty )$
, there exist
![]() $\alpha $
and
$\alpha $
and
![]() $\mu $
satisfying
$\mu $
satisfying
 $$ \begin{align*}\rho=\frac{\alpha^{2}+(\log|\tau|)^{2}}{\pi\alpha}.\end{align*} $$
$$ \begin{align*}\rho=\frac{\alpha^{2}+(\log|\tau|)^{2}}{\pi\alpha}.\end{align*} $$
The constructions in §3 then gives us a Speiser function f in
![]() $\operatorname {\mathcal {S}}_{4}$
whose order is
$\operatorname {\mathcal {S}}_{4}$
whose order is
![]() $\rho $
. This function f has only critical values and no asymptotic values. Moreover, all poles have the multiplicity
$\rho $
. This function f has only critical values and no asymptotic values. Moreover, all poles have the multiplicity
![]() $2$
.
$2$
.
Upper bound. It is clear that the above function f satisfies the conditions of [Reference Bergweiler and KotusBK12, Theorem 1.1]. So we have
 $$ \begin{align*} \operatorname{dim}\operatorname{\mathcal{I}}(f)\leq \frac{2\rho}{1+\rho}. \end{align*} $$
$$ \begin{align*} \operatorname{dim}\operatorname{\mathcal{I}}(f)\leq \frac{2\rho}{1+\rho}. \end{align*} $$
Lower bound. Suppose that
![]() $a_{j}$
are the poles of f, where
$a_{j}$
are the poles of f, where
![]() $\cdots \leq |a_{j}|\leq |a_{j+1}|\leq \cdots $
. Then it follows from (3.10) and Proposition 3.6 that
$\cdots \leq |a_{j}|\leq |a_{j+1}|\leq \cdots $
. Then it follows from (3.10) and Proposition 3.6 that
 $$ \begin{align*}f(z)\sim \bigg(\frac{b_{j}}{z-a_{j}}\bigg)^{2}\quad\text{as } z\to z_{j},\end{align*} $$
$$ \begin{align*}f(z)\sim \bigg(\frac{b_{j}}{z-a_{j}}\bigg)^{2}\quad\text{as } z\to z_{j},\end{align*} $$
where
 $$ \begin{align*}|b_{j}|\sim |a_{j}^{1-\eta}|\sim |a_{j}|^{1-\rho/2}.\end{align*} $$
$$ \begin{align*}|b_{j}|\sim |a_{j}^{1-\eta}|\sim |a_{j}|^{1-\rho/2}.\end{align*} $$
Since f is Speiser, we may take a large
![]() $R_{0}>0$
such that
$R_{0}>0$
such that
![]() $D(0,R_{0})$
contains all singular values of f. Now with
$D(0,R_{0})$
contains all singular values of f. Now with
 $B(R)=\operatorname {\widehat {\mathbb C}}\setminus \overline {D}(0,R)$
and
$B(R)=\operatorname {\widehat {\mathbb C}}\setminus \overline {D}(0,R)$
and
![]() $R>R_{0}$
, each component of
$R>R_{0}$
, each component of
![]() $f^{-1}(B(R))$
is bounded, simply connected and contains one pole of f. Let
$f^{-1}(B(R))$
is bounded, simply connected and contains one pole of f. Let
![]() $U_{j}$
be the component containing the pole
$U_{j}$
be the component containing the pole
![]() $a_{j}$
. By using Koebe’s distortion and one-quarter theorem, we may obtain
$a_{j}$
. By using Koebe’s distortion and one-quarter theorem, we may obtain
 $$ \begin{align} D\bigg(a_{j},\frac{|b_{j}|}{4\sqrt{R}} \bigg)\subset U_{j}\subset D\bigg(a_{j},\frac{2|b_{j}|}{\sqrt{R}} \bigg). \end{align} $$
$$ \begin{align} D\bigg(a_{j},\frac{|b_{j}|}{4\sqrt{R}} \bigg)\subset U_{j}\subset D\bigg(a_{j},\frac{2|b_{j}|}{\sqrt{R}} \bigg). \end{align} $$
See [Reference Aspenberg and CuiAC21, §4] for more details. Moreover, if
![]() $g_{j}$
is an inverse branch of f from some domain
$g_{j}$
is an inverse branch of f from some domain
![]() $\Omega $
to
$\Omega $
to
![]() $U_{j}$
, where
$U_{j}$
, where
![]() $\Omega \subset B(R)$
, then
$\Omega \subset B(R)$
, then
 $$ \begin{align} |g^{\prime}_{j}(z)|\leq B_{1}\,\frac{|b_{j}|}{|z|^{3/2}}\quad\text{for } z\in \Omega. \end{align} $$
$$ \begin{align} |g^{\prime}_{j}(z)|\leq B_{1}\,\frac{|b_{j}|}{|z|^{3/2}}\quad\text{for } z\in \Omega. \end{align} $$
Here
![]() $B_{1}>0$
is some constant.
$B_{1}>0$
is some constant.
We denote by
![]() $\operatorname {diam} (E)$
the diameter of the set E in the plane and by
$\operatorname {diam} (E)$
the diameter of the set E in the plane and by
![]() $\operatorname {diam}_{\chi } (E)$
the spherical diameter of E. The above estimates (4.1) and (4.2) will give us good control over the sizes of the pullbacks of
$\operatorname {diam}_{\chi } (E)$
the spherical diameter of E. The above estimates (4.1) and (4.2) will give us good control over the sizes of the pullbacks of
![]() $U_{k}$
under f for large k. More precisely, for sufficiently large k, we have
$U_{k}$
under f for large k. More precisely, for sufficiently large k, we have
 $$ \begin{align*}\operatorname{diam} g_{j}(U_{k})\leq\sup_{z\in U_{k}}|g^{\prime}_{j}(z)|\operatorname{diam} U_{k} \leq B_{1}\frac{|b_{j}|}{|a_{k}|^{3/2}}\frac{|b_{k}|}{\sqrt{R}},\end{align*} $$
$$ \begin{align*}\operatorname{diam} g_{j}(U_{k})\leq\sup_{z\in U_{k}}|g^{\prime}_{j}(z)|\operatorname{diam} U_{k} \leq B_{1}\frac{|b_{j}|}{|a_{k}|^{3/2}}\frac{|b_{k}|}{\sqrt{R}},\end{align*} $$
and if the indices
![]() $j_{1},\,\ldots ,\,j_{\ell }$
are chosen such that
$j_{1},\,\ldots ,\,j_{\ell }$
are chosen such that
![]() $U_{j_{k}}$
is contained in
$U_{j_{k}}$
is contained in
![]() $B(R)$
, where
$B(R)$
, where
![]() $k=1,\ldots ,\ell $
, we obtain, in terms of the spherical metric,
$k=1,\ldots ,\ell $
, we obtain, in terms of the spherical metric,
 $$ \begin{align} \operatorname{diam}_{\chi}(g_{j_{1}}\circ g_{j_{2}}\circ\cdots\circ g_{j_{\ell-1}})(U_{j_{\ell}})\leq B_{1}^{\ell-1}\,\frac{32}{\sqrt{R}}\,\prod_{k=1}^{\ell}\,\frac{|b_{j_{k}}|}{|a_{j_{k}}|^{3/2}}. \end{align} $$
$$ \begin{align} \operatorname{diam}_{\chi}(g_{j_{1}}\circ g_{j_{2}}\circ\cdots\circ g_{j_{\ell-1}})(U_{j_{\ell}})\leq B_{1}^{\ell-1}\,\frac{32}{\sqrt{R}}\,\prod_{k=1}^{\ell}\,\frac{|b_{j_{k}}|}{|a_{j_{k}}|^{3/2}}. \end{align} $$
We now consider the set
In other words, we are considering those escaping points whose iterates always stay in
![]() $B(R)$
. Apparently, this is a subset of
$B(R)$
. Apparently, this is a subset of
![]() $\operatorname {\mathcal {I}}(f)$
. Let
$\operatorname {\mathcal {I}}(f)$
. Let
![]() $E_{l}$
be the collection of all components V of
$E_{l}$
be the collection of all components V of
![]() $f^{-l}(B(R))$
for which
$f^{-l}(B(R))$
for which
![]() $f^{k}(V)\subset B(R)$
holds for
$f^{k}(V)\subset B(R)$
holds for
![]() $0\leq k\leq l-1$
. We will estimate the sizes of components of
$0\leq k\leq l-1$
. We will estimate the sizes of components of
![]() $E_{l}$
by using (4.3). For such a component V, by definition there exist
$E_{l}$
by using (4.3). For such a component V, by definition there exist
![]() $j_{1},\,\ldots ,\,j_{l-1}$
such that
$j_{1},\,\ldots ,\,j_{l-1}$
such that
 $$ \begin{align*}f^{k}(V)\subset U_{j_{k+1}}\quad\text{for } k=0,1,\ldots,l-1.\end{align*} $$
$$ \begin{align*}f^{k}(V)\subset U_{j_{k+1}}\quad\text{for } k=0,1,\ldots,l-1.\end{align*} $$
So, using (4.3), one can have, for some constants
![]() $B_{2}$
and
$B_{2}$
and
![]() $B_{3}$
,
$B_{3}$
,
 $$ \begin{align*} \operatorname{diam}_{\chi}(V)\leq B_{1}^{\ell-1}\,\frac{32}{\sqrt{R}}\,\prod_{k=1}^{\ell}\,\frac{|b_{j_{k}}|}{|a_{j_{k}}|^{3/2}}=B_{1}^{\ell-1}\,\frac{32}{\sqrt{R}}\,\prod_{k=1}^{\ell}\,\frac{|B_{2}|^{\ell}}{|a_{j_{k}}|^{1/2+\rho/2}}\leq \bigg(\frac{B_{3}}{|R|^{1/2+\rho/2}}\bigg)^{\ell}. \end{align*} $$
$$ \begin{align*} \operatorname{diam}_{\chi}(V)\leq B_{1}^{\ell-1}\,\frac{32}{\sqrt{R}}\,\prod_{k=1}^{\ell}\,\frac{|b_{j_{k}}|}{|a_{j_{k}}|^{3/2}}=B_{1}^{\ell-1}\,\frac{32}{\sqrt{R}}\,\prod_{k=1}^{\ell}\,\frac{|B_{2}|^{\ell}}{|a_{j_{k}}|^{1/2+\rho/2}}\leq \bigg(\frac{B_{3}}{|R|^{1/2+\rho/2}}\bigg)^{\ell}. \end{align*} $$
Put
 $$ \begin{align} d_{\ell}=\bigg(\frac{|B_{3}|}{|R|^{1/2+\rho/2}}\bigg)^{\ell}. \end{align} $$
$$ \begin{align} d_{\ell}=\bigg(\frac{|B_{3}|}{|R|^{1/2+\rho/2}}\bigg)^{\ell}. \end{align} $$
In addition to the term
![]() $d_{\ell }$
defined above, McMullen’s lower-bound estimate for the Hausdorff dimension also involves a lower-bound estimate for the density of
$d_{\ell }$
defined above, McMullen’s lower-bound estimate for the Hausdorff dimension also involves a lower-bound estimate for the density of
![]() $\overline {E}_{l+1}$
in V. Here
$\overline {E}_{l+1}$
in V. Here
![]() $\overline {E}_{\ell }$
represents the union of all elements of
$\overline {E}_{\ell }$
represents the union of all elements of
![]() $E_{\ell }$
. We will also define
$E_{\ell }$
. We will also define
![]() . For this purpose, we consider an annulus
. For this purpose, we consider an annulus
![]() $A(s):=\{z: s<|z|<2s\}$
which is contained in
$A(s):=\{z: s<|z|<2s\}$
which is contained in
![]() $B(R)$
, that is,
$B(R)$
, that is,
![]() $s> R$
. Then the number of
$s> R$
. Then the number of
![]() $U_{j}$
contained in
$U_{j}$
contained in
![]() $A(s)$
is
$A(s)$
is
![]() $B_{4}(n(2s,f)-n(s,f))=B_{5} s^{\rho }$
, where
$B_{4}(n(2s,f)-n(s,f))=B_{5} s^{\rho }$
, where
![]() $B_{4}$
and
$B_{4}$
and
![]() $B_{5}$
are positive numbers. So we have
$B_{5}$
are positive numbers. So we have
 $$ \begin{align*}\operatorname{diam} U_{j}\geq\frac{|b_{j}|}{2\sqrt{R}}=B_{6}\frac{|a_{j}|^{1-\rho/2}}{2\sqrt{R}}\geq \frac{B_{7}}{s^{\rho/2-1/2}}.\end{align*} $$
$$ \begin{align*}\operatorname{diam} U_{j}\geq\frac{|b_{j}|}{2\sqrt{R}}=B_{6}\frac{|a_{j}|^{1-\rho/2}}{2\sqrt{R}}\geq \frac{B_{7}}{s^{\rho/2-1/2}}.\end{align*} $$
where
![]() $B_{6}, B_{7}$
are constants. Therefore,
$B_{6}, B_{7}$
are constants. Therefore,
 $$ \begin{align*}\operatorname{dens}(\overline{E}_{1}, A(s))=\frac{\operatorname{area}(\overline{E}_{1} \cap A(s))}{\operatorname{area} A(s)}\geq \frac{B_{5} s^{\rho}\,\pi(B_{7}/s^{\rho/2-1/2})^{2}}{3\pi s^{2}}=B_{8}\, s,\end{align*} $$
$$ \begin{align*}\operatorname{dens}(\overline{E}_{1}, A(s))=\frac{\operatorname{area}(\overline{E}_{1} \cap A(s))}{\operatorname{area} A(s)}\geq \frac{B_{5} s^{\rho}\,\pi(B_{7}/s^{\rho/2-1/2})^{2}}{3\pi s^{2}}=B_{8}\, s,\end{align*} $$
where
![]() $B_{8}>0$
is a constant. By repeating the argument used in [Reference Aspenberg and CuiAC21, §4], which we do not repeat here, we have the following estimate, for some constant
$B_{8}>0$
is a constant. By repeating the argument used in [Reference Aspenberg and CuiAC21, §4], which we do not repeat here, we have the following estimate, for some constant
![]() $B_{9}>0$
:
$B_{9}>0$
:
 $$ \begin{align} \operatorname{dens}_{\chi}(\overline{E}_{\ell+1}, V)\geq \frac{B_{9}}{R}=:\Delta_{\ell}.\end{align} $$
$$ \begin{align} \operatorname{dens}_{\chi}(\overline{E}_{\ell+1}, V)\geq \frac{B_{9}}{R}=:\Delta_{\ell}.\end{align} $$
Now we can apply McMullen’s result by using (4.4) and (4.5) to obtain
 $$ \begin{align*}\operatorname{dim} E\geq 2-\limsup_{\ell\to\infty}\frac{\sum_{j=1}^{\ell+1}|\log \Delta_{j}|}{|\log d_{\ell}|}\geq 2-\frac{\log B_{9} - \log R}{\log B_{3} - (({1}/{2})+({\rho}/{2}))\log R}.\end{align*} $$
$$ \begin{align*}\operatorname{dim} E\geq 2-\limsup_{\ell\to\infty}\frac{\sum_{j=1}^{\ell+1}|\log \Delta_{j}|}{|\log d_{\ell}|}\geq 2-\frac{\log B_{9} - \log R}{\log B_{3} - (({1}/{2})+({\rho}/{2}))\log R}.\end{align*} $$
With
![]() $R\to \infty $
, we have
$R\to \infty $
, we have
![]() $\operatorname {dim} E\geq {2\rho }/({1+\rho })$
. The next step is to use this estimate to give the estimate for the Hausdorff dimension of the escaping set by taking a sequence
$\operatorname {dim} E\geq {2\rho }/({1+\rho })$
. The next step is to use this estimate to give the estimate for the Hausdorff dimension of the escaping set by taking a sequence
![]() $(R_{k})$
which tends to infinity increasingly and consider those points whose k-iterate lies in
$(R_{k})$
which tends to infinity increasingly and consider those points whose k-iterate lies in
![]() $B(R_{k})$
. This goes in the same way as in the aforementioned reference and so we omit the details. We conclude directly that
$B(R_{k})$
. This goes in the same way as in the aforementioned reference and so we omit the details. We conclude directly that
 $$ \begin{align*}\operatorname{dim}\operatorname{\mathcal{I}}(f)\geq \frac{2\rho}{1+\rho}.\end{align*} $$
$$ \begin{align*}\operatorname{dim}\operatorname{\mathcal{I}}(f)\geq \frac{2\rho}{1+\rho}.\end{align*} $$
Combined with the upper bound discussed above, we have thus finished the proof.
To complete the proof of Theorem 1.1, we still need to find a function in
![]() $\operatorname {\mathcal {S}}_{4}$
with a full-dimensional escaping set. For this purpose, we put
$\operatorname {\mathcal {S}}_{4}$
with a full-dimensional escaping set. For this purpose, we put
This function belongs to
![]() $\operatorname {\mathcal {S}}_{4}$
, as mentioned before.
$\operatorname {\mathcal {S}}_{4}$
, as mentioned before.
Proposition 4.2.
The proof of this result is obtained in the same manner as in [Reference Aspenberg and CuiAC21, §4.3]. We leave the details to the interested reader.
Acknowledgements
We would like to thank the referee for many useful comments and corrections. The second author would also like to thank Vergstiftelsen for financial support.