Article contents
Dynamics and eigenvalues in dimension zero
Published online by Cambridge University Press: 04 January 2019
Abstract
Let 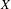 $X$ be a compact, metric and totally disconnected space and let
$X$ be a compact, metric and totally disconnected space and let 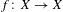 $f:X\rightarrow X$ be a continuous map. We relate the eigenvalues of
$f:X\rightarrow X$ be a continuous map. We relate the eigenvalues of 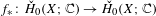 $f_{\ast }:\check{H}_{0}(X;\mathbb{C})\rightarrow \check{H}_{0}(X;\mathbb{C})$ to dynamical properties of
$f_{\ast }:\check{H}_{0}(X;\mathbb{C})\rightarrow \check{H}_{0}(X;\mathbb{C})$ to dynamical properties of 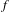 $f$, roughly showing that if the dynamics is complicated then every complex number of modulus different from 0, 1 is an eigenvalue. This stands in contrast with a classical inequality of Manning that bounds the entropy of
$f$, roughly showing that if the dynamics is complicated then every complex number of modulus different from 0, 1 is an eigenvalue. This stands in contrast with a classical inequality of Manning that bounds the entropy of 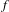 $f$ below by the spectral radius of
$f$ below by the spectral radius of 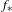 $f_{\ast }$.
$f_{\ast }$.
MSC classification
- Type
- Original Article
- Information
- Copyright
- © Cambridge University Press, 2019
References
- 1
- Cited by



