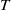Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Solecki, Sławomir
2014.
Unitary representations of the groups of measurable and continuous functions with values in the circle.
Journal of Functional Analysis,
Vol. 267,
Issue. 9,
p.
3105.
Gao, Su
and
Hill, Aaron
2016.
Topological isomorphism for rank-1 systems.
Journal d'Analyse Mathématique,
Vol. 128,
Issue. 1,
p.
1.
SCHNURR, MIKE
2019.
Generic properties of extensions.
Ergodic Theory and Dynamical Systems,
Vol. 39,
Issue. 11,
p.
3144.
ETEDADIALIABADI, MAHMOOD
2020.
Generic behavior of a measure-preserving transformation.
Ergodic Theory and Dynamical Systems,
Vol. 40,
Issue. 4,
p.
904.
Neretin, Yu. A.
2021.
Polyhomomorphisms of locally compact groups.
Sbornik: Mathematics,
Vol. 212,
Issue. 2,
p.
185.
Stepin, Anatoly
and
Tikhonov, Sergey
2021.
Topology, Geometry, and Dynamics.
Vol. 772,
Issue. ,
p.
311.
Neretin, Yurii Aleksandrovich
2021.
Полигомоморфизмы локально компактных групп.
Математический сборник,
Vol. 212,
Issue. 2,
p.
53.
Glasner, E.
Thouvenot, J.-P.
and
Weiss, B.
2022.
On some generic classes of ergodic measure preserving transformations.
Transactions of the Moscow Mathematical Society,
Vol. 82,
Issue. 0,
p.
15.
Solecki, Sławomir
2023.
Generic measure preserving transformations and the closed groups they generate.
Inventiones mathematicae,
Vol. 231,
Issue. 2,
p.
805.