Published online by Cambridge University Press: 15 June 2020
Furstenberg [Disjointness in ergodic theory, minimal sets, and a problem in Diophantine approximation. Math. Syst. Theory1 (1967), 1–49] calculated the Hausdorff and Minkowski dimensions of one-sided subshifts in terms of topological entropy. We generalize this to 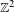 $\mathbb{Z}^{2}$-subshifts. Our generalization involves mean dimension theory. We calculate the metric mean dimension and the mean Hausdorff dimension of
$\mathbb{Z}^{2}$-subshifts. Our generalization involves mean dimension theory. We calculate the metric mean dimension and the mean Hausdorff dimension of 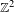 $\mathbb{Z}^{2}$-subshifts with respect to a subaction of
$\mathbb{Z}^{2}$-subshifts with respect to a subaction of  $\mathbb{Z}$. The resulting formula is quite analogous to Furstenberg’s theorem. We also calculate the rate distortion dimension of
$\mathbb{Z}$. The resulting formula is quite analogous to Furstenberg’s theorem. We also calculate the rate distortion dimension of 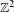 $\mathbb{Z}^{2}$-subshifts in terms of Kolmogorov–Sinai entropy.
$\mathbb{Z}^{2}$-subshifts in terms of Kolmogorov–Sinai entropy.