No CrossRef data available.
Article contents
Global dynamical properties of Euler and backward Euler
Published online by Cambridge University Press: 19 September 2008
Abstract
We investigate the global dynamics of both the Euler and backward Euler algorithms as applied to polynomial vector fields on the Riemann sphere 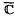 = ℂ ∪ {∞}. The geometry and dynamics of solutions at infinity is seen to play an important role in organizing the global dynamics of the flow, and we show how to modify both algorithms to account for this structure, thereby obtaining global approximations to the flow.
= ℂ ∪ {∞}. The geometry and dynamics of solutions at infinity is seen to play an important role in organizing the global dynamics of the flow, and we show how to modify both algorithms to account for this structure, thereby obtaining global approximations to the flow.
- Type
- Research Article
- Information
- Copyright
- Copyright © Cambridge University Press 1993


