Article contents
Closest integer polynomial multiple recurrence along shifted primes
Published online by Cambridge University Press: 20 September 2016
Abstract
Following an approach presented by Frantzikinakis et al [The polynomial multidimensional Szemerédi theorem along shifted primes. Israel J. Math.194(1) (2013), 331–348], we show that the parameters in the multidimensional Szemerédi theorem for closest integer polynomials have non-empty intersection with the set of shifted primes 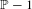 $\mathbb{P}-1$ (or, similarly, of
$\mathbb{P}-1$ (or, similarly, of 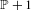 $\mathbb{P}+1$). Using the Furstenberg correspondence principle, we show this result by recasting it as a polynomial multiple recurrence result in measure ergodic theory. Furthermore, we obtain integer part polynomial convergence results by the same method, which is a transference principle that enables one to deduce results for
$\mathbb{P}+1$). Using the Furstenberg correspondence principle, we show this result by recasting it as a polynomial multiple recurrence result in measure ergodic theory. Furthermore, we obtain integer part polynomial convergence results by the same method, which is a transference principle that enables one to deduce results for  $\mathbb{Z}$-actions from results for flows. We also give some applications of our approach to Gowers uniform sets.
$\mathbb{Z}$-actions from results for flows. We also give some applications of our approach to Gowers uniform sets.
- Type
- Original Article
- Information
- Copyright
- © Cambridge University Press, 2016
References
- 7
- Cited by


