Article contents
The bifurcation locus for numbers of bounded type
Published online by Cambridge University Press: 08 April 2021
Abstract
We define a family
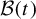 $\mathcal {B}(t)$
of compact subsets of the unit interval which provides a filtration of the set of numbers whose continued fraction expansion has bounded digits. We study how the set
$\mathcal {B}(t)$
of compact subsets of the unit interval which provides a filtration of the set of numbers whose continued fraction expansion has bounded digits. We study how the set
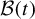 $\mathcal {B}(t)$
changes as the parameter t ranges in
$\mathcal {B}(t)$
changes as the parameter t ranges in
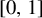 $[0,1]$
, and see that the family undergoes period-doubling bifurcations and displays the same transition pattern from periodic to chaotic behaviour as the family of real quadratic polynomials. The set
$[0,1]$
, and see that the family undergoes period-doubling bifurcations and displays the same transition pattern from periodic to chaotic behaviour as the family of real quadratic polynomials. The set
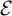 $\mathcal {E}$
of bifurcation parameters is a fractal set of measure zero and Hausdorff dimension
$\mathcal {E}$
of bifurcation parameters is a fractal set of measure zero and Hausdorff dimension
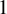 $1$
. The Hausdorff dimension of
$1$
. The Hausdorff dimension of
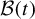 $\mathcal {B}(t)$
varies continuously with the parameter, and we show that the dimension of each individual set equals the dimension of the corresponding section of the bifurcation set
$\mathcal {B}(t)$
varies continuously with the parameter, and we show that the dimension of each individual set equals the dimension of the corresponding section of the bifurcation set
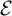 $\mathcal {E}$
.
$\mathcal {E}$
.
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
- 4
- Cited by



