INTRODUCTION
Dengue is a human disease caused by four related but distinct strains of flavivirus and is transmitted by urban vectors [Reference Monath, Heinz, Fields and Howley1–Reference Amaku3]. It is currently considered the most important vector-borne infection, affecting almost 400 million people every year in tropical countries [Reference Bhatt4]. Dengue outbreaks recur with patterns of different magnitude and frequency that challenge our understanding based on the current knowledge of environment–mosquito–human interactions.
The Brazilian government maintains a database of the weekly incidence of dengue for a large number of cities in all regions of the country. This database reveals a great variety of patterns as shown in the four examples given in Figure 1.

Fig. 1. Four different patterns of time distribution of dengue outbreaks in Brazil, 2000–2014.
This paper has three aims:
-
(1) To understand how so many different patterns originate and to determine the mechanism underlying this diversity.
-
(2) To propose a mathematical model to explain the patterns and to investigate if the mechanisms involved are unique.
-
(3) To identify the variables and parameters that can be used to predict when dengue transmission will cease in a certain city and, if it persists, where it will occur in the future with a certain probability. Because these probabilities depend on particular measurements that may be demanding, our third goal should be entitled: how to forecast dengue epidemics.
The paper is organized as follows. In the following section, we describe a very simple model of dengue epidemics that incorporates elements that are novel to the usual dengue models. These elements have been partly described in two previous papers by Amaku and colleagues [Reference Amaku3, Reference Massad5]. This model is in fact the classical Ross–Macdonald model, but it has been modified to avoid simple pitfalls in its application [Reference Massad5].
Next, we analyse the model and show that it can predict any pattern of epidemics. We also illustrate the production of patterns using two mechanisms: the movement of people and seasonality. In the Results section, we introduce the calculation of a few quantities that should allow public authorities to make predictions about future events so that resources can be better allocated. Finally, we present a summary of our findings.
HUMANS ARE THE REAL VECTOR OF DENGUE
Aedes aegypti, the dengue mosquito, has a very short lifespan typically lasting for 1 week [Reference Amaku3] and has a short flight range of ~100 m. During these short spans of life and flight range the mosquito covers a very small area of the region where dengue epidemics occur. Hence, considering that in large urban areas dengue circulates from one neighbourhood to another, we must assume that dengue is carried by humans who are infected but are still able to circulate.
Based on this assumption, we propose a very simple model that consists of N regions of a city that are more or less geographically separate from one another other, in the sense that the inhabitants of each of those regions rarely visit the other regions (or visit at the ‘wrong’ time of day). By this, we mean visits to other regions at a time which would allow humans to be bitten by mosquitoes and acquire the infection. We will show that this explains why, in some cities, there can be a dengue epidemic in one district and not in another nearby neighbourhood during the same transmission season.
The model consists of the following system of differential equations. To help the reader, the meaning of the symbols are given in Table 1. H Si , HIi and H Ri are the densities of susceptible, infected and recovered individuals, respectively, who live in neighbourhood i. M Si , MLi and M Ii are the densities of susceptible, latent and infected mosquitoes, respectively, that live in neighbourhood i. The neighbourhoods are assumed to be homogeneous, and the population density is obtained by multiplying the density by the area of each neighbourhood.
Table 1. Variables, parameters, their biological meaning and the values of system (1)

* ϕ is usually taken to be exp(–μ M τ).
The equations that describe the system are:
 $$\left.{\eqalign{\displaystyle{{{\rm d}H_{Si}} \over {{\rm d}t}} &= - a_1bH_{Si}\sum\limits_j {\beta _{ij}^H \displaystyle{{M_{Ij}} \over {N_{Hj}}}} - \mu _HH_{Si} + \Lambda _i^H, \cr \displaystyle{{{\rm d}H_{Ii}} \over {{\rm d}t}} &= a_1bH_{Si}\sum\limits_j {\beta _{ij}^H \displaystyle{{M_{Ij}} \over {N_{Hj}}}} - \left( {\mu _H + \gamma _H + \alpha _H} \right)H_{Ii}, \cr \displaystyle{{{\rm d}H_{Ri}} \over {{\rm d}t}} &= \gamma _HH_{Ii} - \mu _HH_{Ri}, \cr \displaystyle{{{\rm d}M_{Si}} \over {{\rm d}t}} &= - a_2c\displaystyle{{M_{Si}} \over {N_{Hi}}}\sum\limits_j {\beta _{ij}^M H_{Ij}} - \mu _MM_{Si} + \Lambda _i^M, \cr \displaystyle{{{\rm d}M_{Li}} \over {{\rm d}t}} &= a_2c\displaystyle{{M_{Si}} \over {N_{Hi}}}\sum\limits_j {\beta _{ij}^M H_{Ij}} - a_2c\phi \displaystyle{{M_{Si}\left( {t - \tau} \right)} \over {N_{Hi}\left( {t - \tau} \right)}}\sum\limits_j {\beta _{ij}^M H_{Ij}\left( {t - \tau} \right)} - \mu _MM_{Li}, \cr \displaystyle{{{\rm d}M_{Ii}} \over {{\rm d}t}} &= a_2c\phi \displaystyle{{M_{Si}\left( {t - \tau} \right)} \over {N_{Hi}\left( {t - \tau} \right)}}\sum\limits_j {\beta _{ij}^M H_{Ij}\left( {t - \tau} \right)} - \mu _MM_{Ii}.}}\right\}$$
$$\left.{\eqalign{\displaystyle{{{\rm d}H_{Si}} \over {{\rm d}t}} &= - a_1bH_{Si}\sum\limits_j {\beta _{ij}^H \displaystyle{{M_{Ij}} \over {N_{Hj}}}} - \mu _HH_{Si} + \Lambda _i^H, \cr \displaystyle{{{\rm d}H_{Ii}} \over {{\rm d}t}} &= a_1bH_{Si}\sum\limits_j {\beta _{ij}^H \displaystyle{{M_{Ij}} \over {N_{Hj}}}} - \left( {\mu _H + \gamma _H + \alpha _H} \right)H_{Ii}, \cr \displaystyle{{{\rm d}H_{Ri}} \over {{\rm d}t}} &= \gamma _HH_{Ii} - \mu _HH_{Ri}, \cr \displaystyle{{{\rm d}M_{Si}} \over {{\rm d}t}} &= - a_2c\displaystyle{{M_{Si}} \over {N_{Hi}}}\sum\limits_j {\beta _{ij}^M H_{Ij}} - \mu _MM_{Si} + \Lambda _i^M, \cr \displaystyle{{{\rm d}M_{Li}} \over {{\rm d}t}} &= a_2c\displaystyle{{M_{Si}} \over {N_{Hi}}}\sum\limits_j {\beta _{ij}^M H_{Ij}} - a_2c\phi \displaystyle{{M_{Si}\left( {t - \tau} \right)} \over {N_{Hi}\left( {t - \tau} \right)}}\sum\limits_j {\beta _{ij}^M H_{Ij}\left( {t - \tau} \right)} - \mu _MM_{Li}, \cr \displaystyle{{{\rm d}M_{Ii}} \over {{\rm d}t}} &= a_2c\phi \displaystyle{{M_{Si}\left( {t - \tau} \right)} \over {N_{Hi}\left( {t - \tau} \right)}}\sum\limits_j {\beta _{ij}^M H_{Ij}\left( {t - \tau} \right)} - \mu _MM_{Ii}.}}\right\}$$
where the indices i,j = 1, … , N correspond to different neighbourhoods, ϕ is the proportion of latent mosquitoes that survive the incubation period τ, and
As an example to clarify the above equations, let us consider two neighbourhoods and two human and insect populations. Then, we have:
 $$\eqalign{ \displaystyle{{{\rm d}H_{S1}} \over {{\rm d}t}} &= - a_1bH_{S1}\left[ {\left( {1 - \beta _{12}^H} \right)\displaystyle{{M_{I1}} \over {N_{H1}}} + \beta _{12}^H \displaystyle{{M_{I2}} \over {N_{H2}}}} \right] - \mu _HH_{S1} + \Lambda _1^H, \cr \displaystyle{{{\rm d}H_{S2}} \over {{\rm d}t}} &= - a_1bH_{S2}\left[ {\beta _{21}^H \displaystyle{{M_{I1}} \over {N_{H1}}} + \left( {1 - \beta _{21}^H} \right)\displaystyle{{M_{I2}} \over {N_{H2}}}} \right] - \mu _HH_{S2} + \Lambda _2^H, \cr \displaystyle{{{\rm d}H_{I1}} \over {{\rm d}t}} &= a_1bH_{S1}\left[ {\left( {1 - \beta _{12}^H} \right)\displaystyle{{M_{I1}} \over {N_{H1}}} + \beta _{12}^H \displaystyle{{M_{I2}} \over {N_{H2}}}} \right] - \left( {\mu _H + \gamma _H + \alpha _H} \right)H_{I1}, \cr \displaystyle{{{\rm d}H_{I2}} \over {{\rm d}t}} &= a_1bH_{S2}\left[ {\beta _{21}^H \displaystyle{{M_{I1}} \over {N_{H1}}} + \left( {1 - \beta _{21}^H} \right)\displaystyle{{M_{I2}} \over {N_{H2}}}} \right] - \left( {\mu _H + \gamma _H + \alpha _H} \right)H_{I2}, \cr \displaystyle{{{\rm d}H_{R1}} \over {{\rm d}t}} &= \gamma _HH_{I1} - \mu _HH_{R1}, \cr \displaystyle{{{\rm d}H_{R2}} \over {{\rm d}t}} &= \gamma _HH_{I2} - \mu _HH_{R2}.} $$
$$\eqalign{ \displaystyle{{{\rm d}H_{S1}} \over {{\rm d}t}} &= - a_1bH_{S1}\left[ {\left( {1 - \beta _{12}^H} \right)\displaystyle{{M_{I1}} \over {N_{H1}}} + \beta _{12}^H \displaystyle{{M_{I2}} \over {N_{H2}}}} \right] - \mu _HH_{S1} + \Lambda _1^H, \cr \displaystyle{{{\rm d}H_{S2}} \over {{\rm d}t}} &= - a_1bH_{S2}\left[ {\beta _{21}^H \displaystyle{{M_{I1}} \over {N_{H1}}} + \left( {1 - \beta _{21}^H} \right)\displaystyle{{M_{I2}} \over {N_{H2}}}} \right] - \mu _HH_{S2} + \Lambda _2^H, \cr \displaystyle{{{\rm d}H_{I1}} \over {{\rm d}t}} &= a_1bH_{S1}\left[ {\left( {1 - \beta _{12}^H} \right)\displaystyle{{M_{I1}} \over {N_{H1}}} + \beta _{12}^H \displaystyle{{M_{I2}} \over {N_{H2}}}} \right] - \left( {\mu _H + \gamma _H + \alpha _H} \right)H_{I1}, \cr \displaystyle{{{\rm d}H_{I2}} \over {{\rm d}t}} &= a_1bH_{S2}\left[ {\beta _{21}^H \displaystyle{{M_{I1}} \over {N_{H1}}} + \left( {1 - \beta _{21}^H} \right)\displaystyle{{M_{I2}} \over {N_{H2}}}} \right] - \left( {\mu _H + \gamma _H + \alpha _H} \right)H_{I2}, \cr \displaystyle{{{\rm d}H_{R1}} \over {{\rm d}t}} &= \gamma _HH_{I1} - \mu _HH_{R1}, \cr \displaystyle{{{\rm d}H_{R2}} \over {{\rm d}t}} &= \gamma _HH_{I2} - \mu _HH_{R2}.} $$
and
 $$\left.{\eqalign{ \displaystyle{{{\rm d}M_{S1}} \over {{\rm d}t}} &= - a_2c\displaystyle{{M_{S1}} \over {N_{H1}}}\left[ {\left( {1 - \beta _{12}^M} \right)H_{I1} + \beta _{12}^M H_{I2}} \right] - \mu _MM_{S1} + \Lambda _1^M, \cr \displaystyle{{{\rm d}M_{S2}} \over {{\rm d}t}} &= - a_2c\displaystyle{{M_{S2}} \over {N_{H2}}}\left[ {\beta _{21}^M H_{I1} + \left( {1 - \beta _{21}^M} \right)H_{I2}} \right] - \mu _MM_{S2} + \Lambda _2^M, \cr \displaystyle{{{\rm d}M_{L1}} \over {{\rm d}t}} &= a_2c\displaystyle{{M_{S1}} \over {N_{H1}}}\left[ {\left( {1 - \beta _{12}^M} \right)H_{I1} + \beta _{12}^M H_{I2}} \right] - a_2c\phi \displaystyle{{M_{S1}\left( {t - \tau} \right)} \over {N_{H1}\left( {t - \tau} \right)}}\left[ {\left( {1 - \beta _{12}^M} \right)H_{I1}\left( {t - \tau} \right) + \beta _{12}^M H_{I2}\left( {t - \tau} \right)} \right] - \mu _MM_{L1}, \cr {\rm} \displaystyle{{{\rm d}M_{L2}} \over {{\rm d}t}} &= a_2c\displaystyle{{M_{S2}} \over {N_{H2}}}\left[ {\beta _{21}^M H_{I1}+ \left( {1 - \beta _{21}^M} \right) H_{I2}} \right] - a_2c\phi \displaystyle{{M_{S2}\left( {t - \tau} \right)} \over {N_{H2}\left( {t - \tau} \right)}}\left[ {\beta _{21}^M H_{I1}\left( {t - \tau} \right) + \left( {1 - \beta _{21}^M} \right)H_{I2}\left( {t - \tau} \right)} \right] - \mu _MM_{L2}, \cr \displaystyle{{{\rm d}M_{I1}} \over {{\rm d}t}} &= a_2c\phi \displaystyle{{M_{S1}\left( {t - \tau} \right)} \over {N_{H1}\left( {t - \tau} \right)}} \left[ {\left( {1 - \beta _{12}^M} \right)H_{I1}\left( {t - \tau} \right) + \beta _{12}^M H_{I2}\left( {t - \tau} \right)} \right] - \mu _MM_{I1} \cr \displaystyle{{{\rm d}M_{I2}} \over {{\rm d}t}} &= a_2c\phi \displaystyle{{M_{S2}\left( {t - \tau} \right)} \over {N_{H2}\left( {t - \tau} \right)}} \left[ {\beta _{21}^M H_{I1}\left( {t - \tau} \right) + \left( {1 - \beta _{21}^M} \right)H_{I2}\left( {t - \tau} \right)} \right] - \mu _MM_{I2}.\quad}}\right\}$$
$$\left.{\eqalign{ \displaystyle{{{\rm d}M_{S1}} \over {{\rm d}t}} &= - a_2c\displaystyle{{M_{S1}} \over {N_{H1}}}\left[ {\left( {1 - \beta _{12}^M} \right)H_{I1} + \beta _{12}^M H_{I2}} \right] - \mu _MM_{S1} + \Lambda _1^M, \cr \displaystyle{{{\rm d}M_{S2}} \over {{\rm d}t}} &= - a_2c\displaystyle{{M_{S2}} \over {N_{H2}}}\left[ {\beta _{21}^M H_{I1} + \left( {1 - \beta _{21}^M} \right)H_{I2}} \right] - \mu _MM_{S2} + \Lambda _2^M, \cr \displaystyle{{{\rm d}M_{L1}} \over {{\rm d}t}} &= a_2c\displaystyle{{M_{S1}} \over {N_{H1}}}\left[ {\left( {1 - \beta _{12}^M} \right)H_{I1} + \beta _{12}^M H_{I2}} \right] - a_2c\phi \displaystyle{{M_{S1}\left( {t - \tau} \right)} \over {N_{H1}\left( {t - \tau} \right)}}\left[ {\left( {1 - \beta _{12}^M} \right)H_{I1}\left( {t - \tau} \right) + \beta _{12}^M H_{I2}\left( {t - \tau} \right)} \right] - \mu _MM_{L1}, \cr {\rm} \displaystyle{{{\rm d}M_{L2}} \over {{\rm d}t}} &= a_2c\displaystyle{{M_{S2}} \over {N_{H2}}}\left[ {\beta _{21}^M H_{I1}+ \left( {1 - \beta _{21}^M} \right) H_{I2}} \right] - a_2c\phi \displaystyle{{M_{S2}\left( {t - \tau} \right)} \over {N_{H2}\left( {t - \tau} \right)}}\left[ {\beta _{21}^M H_{I1}\left( {t - \tau} \right) + \left( {1 - \beta _{21}^M} \right)H_{I2}\left( {t - \tau} \right)} \right] - \mu _MM_{L2}, \cr \displaystyle{{{\rm d}M_{I1}} \over {{\rm d}t}} &= a_2c\phi \displaystyle{{M_{S1}\left( {t - \tau} \right)} \over {N_{H1}\left( {t - \tau} \right)}} \left[ {\left( {1 - \beta _{12}^M} \right)H_{I1}\left( {t - \tau} \right) + \beta _{12}^M H_{I2}\left( {t - \tau} \right)} \right] - \mu _MM_{I1} \cr \displaystyle{{{\rm d}M_{I2}} \over {{\rm d}t}} &= a_2c\phi \displaystyle{{M_{S2}\left( {t - \tau} \right)} \over {N_{H2}\left( {t - \tau} \right)}} \left[ {\beta _{21}^M H_{I1}\left( {t - \tau} \right) + \left( {1 - \beta _{21}^M} \right)H_{I2}\left( {t - \tau} \right)} \right] - \mu _MM_{I2}.\quad}}\right\}$$
From the above equations, it becomes clear that only humans travel from one neighbourhood to another. For example, the proportion of susceptible and infected humans from neighbourhood 1 that visit neighbourhood 2 is denoted as
![]() $\beta _{12}^H $
. In addition, we assume that
$\beta _{12}^H $
. In addition, we assume that
Seasonal fluctuations in the number of mosquitoes is very common and may influence the pattern and duration of outbreaks. To introduce these fluctuations, we replace the mosquito equations with:
 $$\left.{\eqalign{ \displaystyle{{{\rm d}M_{S1}} \over {{\rm d}t}} &= \left[ {1 + M_2^1 \left( {\displaystyle{{2\pi f} \over {\mu _M}}} \right)\cos \left( {2\pi ft} \right)} \right]\mu _M(M_{S1} + M_{L1} + M_{I1}) - a_2c\displaystyle{{M_{S1}} \over {N_{H1}}}\left[ {\left( {1 - \beta _{12}^M} \right)H_{I1} + \beta _{12}^M H_{I2}} \right] - \mu _MM_{S1}\;,\,\cr &\;\quad \quad M_2^1 \left( {\displaystyle{{2\pi f} \over {\mu _M}}} \right) \lt 1, \cr \displaystyle{{{\rm d}M_{S2}} \over {{\rm d}t}} &= \left[ {1 + M_2^2 \left( {\displaystyle{{2\pi f} \over {\mu _M}}} \right)\cos \left( {2\pi ft} \right)} \right] \mu _M(M_{S1} + M_{L1} + M_{I1}) - a_2c\displaystyle{{M_{S2}} \over {N_{H2}}}\left[ {\beta _{21}^M H_{I1} + \left( {1 - \beta _{21}^M} \right)H_{I2}} \right] - \mu _MM_{S2}\;, \;\;\cr &\quad \quad M_2^2 \left( {\displaystyle{{2\pi f} \over {\mu _M}}} \right) \lt 1, \cr \displaystyle{{{\rm d}M_{L1}} \over {{\rm d}t}} &= a_2c\displaystyle{{M_{S1}} \over {N_{H1}}}\left[ {\left( {1 - \beta _{12}^M} \right)H_{I1} + \beta _{12}^M H_{I2}} \right] - a_2c\phi \displaystyle{{M_{S1}\left( {t - \tau} \right)} \over {N_{H1}\left( {t - \tau} \right)}}\left[ {\left( {1 - \beta _{12}^M} \right)H_{I1}\left( {t - \tau} \right) + \beta _{12}^M H_{I2}\left( {t - \tau} \right)} \right] - \mu _MM_{L1}{\rm,} \cr \displaystyle{{{\rm d}M_{L2}} \over {{\rm d}t}} &= a_2c\displaystyle{{M_{S2}} \over {N_{H2}}}\left[ {\beta _{21}^M H_{I1} + \left( {1 - \beta _{21}^M} \right)H_{I2}} \right] - a_2c\phi \displaystyle{{M_{S2}\left( {t - \tau} \right)} \over {N_{H2}\left( {t - \tau} \right)}}\left[ {\beta _{21}^M H_{I1}\left( {t - \tau} \right) + \left( {1 - \beta _{21}^M} \right)H_{I2}\left( {t - \tau} \right)} \right] - \mu _MM_{L2}, \cr \displaystyle{{{\rm d}M_{I1}} \over {{\rm d}t}} &= a_2c\phi \displaystyle{{M_{S1}\left( {t - \tau} \right)} \over {N_{H1}\left( {t - \tau} \right)}}\left[ {\left( {1 - \beta _{12}^M} \right)H_{I1}\left( {t - \tau} \right) + \beta _{12}^M H_{I2}\left( {t - \tau} \right)} \right] - \mu _MM_{I1}, \cr \displaystyle{{{\rm d}M_{I2}} \over {{\rm d}t}} &= a_2c\phi \displaystyle{{M_{S2}\left( {t - \tau} \right)} \over {N_{H2}\left( {t - \tau} \right)}} \left[ {\beta _{21}^M H_{I1}\left( {t - \tau} \right) + \left( {1 - \beta _{21}^M} \right)H_{I2}\left( {t - \tau} \right)} \right] - \mu _MM_{I2}.\quad \cr &\cr& M_{L1}(0) = M_{L2}(0) = 1 \cr & M_{I1}(0) = M_{I2}(0) = 0}}\right\}$$
$$\left.{\eqalign{ \displaystyle{{{\rm d}M_{S1}} \over {{\rm d}t}} &= \left[ {1 + M_2^1 \left( {\displaystyle{{2\pi f} \over {\mu _M}}} \right)\cos \left( {2\pi ft} \right)} \right]\mu _M(M_{S1} + M_{L1} + M_{I1}) - a_2c\displaystyle{{M_{S1}} \over {N_{H1}}}\left[ {\left( {1 - \beta _{12}^M} \right)H_{I1} + \beta _{12}^M H_{I2}} \right] - \mu _MM_{S1}\;,\,\cr &\;\quad \quad M_2^1 \left( {\displaystyle{{2\pi f} \over {\mu _M}}} \right) \lt 1, \cr \displaystyle{{{\rm d}M_{S2}} \over {{\rm d}t}} &= \left[ {1 + M_2^2 \left( {\displaystyle{{2\pi f} \over {\mu _M}}} \right)\cos \left( {2\pi ft} \right)} \right] \mu _M(M_{S1} + M_{L1} + M_{I1}) - a_2c\displaystyle{{M_{S2}} \over {N_{H2}}}\left[ {\beta _{21}^M H_{I1} + \left( {1 - \beta _{21}^M} \right)H_{I2}} \right] - \mu _MM_{S2}\;, \;\;\cr &\quad \quad M_2^2 \left( {\displaystyle{{2\pi f} \over {\mu _M}}} \right) \lt 1, \cr \displaystyle{{{\rm d}M_{L1}} \over {{\rm d}t}} &= a_2c\displaystyle{{M_{S1}} \over {N_{H1}}}\left[ {\left( {1 - \beta _{12}^M} \right)H_{I1} + \beta _{12}^M H_{I2}} \right] - a_2c\phi \displaystyle{{M_{S1}\left( {t - \tau} \right)} \over {N_{H1}\left( {t - \tau} \right)}}\left[ {\left( {1 - \beta _{12}^M} \right)H_{I1}\left( {t - \tau} \right) + \beta _{12}^M H_{I2}\left( {t - \tau} \right)} \right] - \mu _MM_{L1}{\rm,} \cr \displaystyle{{{\rm d}M_{L2}} \over {{\rm d}t}} &= a_2c\displaystyle{{M_{S2}} \over {N_{H2}}}\left[ {\beta _{21}^M H_{I1} + \left( {1 - \beta _{21}^M} \right)H_{I2}} \right] - a_2c\phi \displaystyle{{M_{S2}\left( {t - \tau} \right)} \over {N_{H2}\left( {t - \tau} \right)}}\left[ {\beta _{21}^M H_{I1}\left( {t - \tau} \right) + \left( {1 - \beta _{21}^M} \right)H_{I2}\left( {t - \tau} \right)} \right] - \mu _MM_{L2}, \cr \displaystyle{{{\rm d}M_{I1}} \over {{\rm d}t}} &= a_2c\phi \displaystyle{{M_{S1}\left( {t - \tau} \right)} \over {N_{H1}\left( {t - \tau} \right)}}\left[ {\left( {1 - \beta _{12}^M} \right)H_{I1}\left( {t - \tau} \right) + \beta _{12}^M H_{I2}\left( {t - \tau} \right)} \right] - \mu _MM_{I1}, \cr \displaystyle{{{\rm d}M_{I2}} \over {{\rm d}t}} &= a_2c\phi \displaystyle{{M_{S2}\left( {t - \tau} \right)} \over {N_{H2}\left( {t - \tau} \right)}} \left[ {\beta _{21}^M H_{I1}\left( {t - \tau} \right) + \left( {1 - \beta _{21}^M} \right)H_{I2}\left( {t - \tau} \right)} \right] - \mu _MM_{I2}.\quad \cr &\cr& M_{L1}(0) = M_{L2}(0) = 1 \cr & M_{I1}(0) = M_{I2}(0) = 0}}\right\}$$
In system (3),
![]() $M_2^1 $
and
$M_2^1 $
and
![]() $M_2^2 $
define the amplitude of the oscillations in the density of mosquitoes due to seasonality (this is a schematic model). In the absence of infection, the equation for the mosquito populations can be solved exactly. The equation for the density of mosquitoes and its solutions are:
$M_2^2 $
define the amplitude of the oscillations in the density of mosquitoes due to seasonality (this is a schematic model). In the absence of infection, the equation for the mosquito populations can be solved exactly. The equation for the density of mosquitoes and its solutions are:
and
The above model for seasonality can be easily modified. For instance, an upper limit to the mosquito population can be introduced such that the model becomes more realistic. We did this and the qualitative results described in Figure 6 below showed very little change.
Note that, in system (3), the total number of mosquitoes is not affected by the infection. This is a very good approximation for dengue because only a very small number of mosquitoes are infected, and their life expectancy is not affected by the disease. However, the total number of infections varies with the climatic factor compared to the case; in which, the number of mosquitoes is constant. It also varies with the moment of time that the infection is ‘introduced’ into the population.
If the disease is introduced, for example in district 1, it will eventually spread to other districts. This, however, can be a very slow process and because the data reported represent the number of cases in a given city per month, the duration of epidemics can be very long because the disease is ‘travelling’ through the city, carried by humans.
Remark 1 Choosing
![]() $\Lambda _i^H $
and
$\Lambda _i^H $
and
![]() $\Lambda _i^M $
in such a way that the human and the mosquito populations are kept constant, then dividing the equations of system (1) by N
Hi
and N
Mi
, we obtain equations for the proportions. Of course, if there is seasonality, this cannot be done for the mosquito population.
$\Lambda _i^M $
in such a way that the human and the mosquito populations are kept constant, then dividing the equations of system (1) by N
Hi
and N
Mi
, we obtain equations for the proportions. Of course, if there is seasonality, this cannot be done for the mosquito population.
Remark 2 The above equations refer to a single dengue strain circulating in a given population. In some places, however, more than one serotype can circulate simultaneously in the same community. If we assume that the circulation of one virus does not interfere with the other, then the two viruses can be treated separately.
Remark 3 In this paper, we assumed two different biting rates (denoted a 1 and a 2) for the infected and non-infected mosquitoes, respectively. This was done for the sake of generality. In the case of dengue, it is accepted that they are both equal, although this may not be true for other vector-borne infections (e.g. in the case of plague [Reference Massad5]).
ANALYSIS OF THE MODEL
The system of equations given above does not have an analytical solution, even when there is just one neighbourhood and no seasonal fluctuations. Even if an analytical solution existed, it would be so complicated that it would be of no use. We, therefore, list a number of numerical results derived using the system and show how they can be used.
The simple Ross–Macdonald model
Consider that we have just one human and one mosquito population. As noted by Amaku et al. [Reference Amaku6], this simple system is solved by assuming that an initial population of infected hosts (either humans or mosquitoes) is uniformly distributed over the area that is being studied. The result is a large outbreak, as shown in Figure 1. This can be explained as follows:
If the basic reproduction number [Reference Lopez7–Reference Garba9] of this model is >1, the outbreak increases up to a certain point where the number of susceptible individuals diminishes to a certain value. The infection then disappears for a number of years. This is not what is observed in real outbreaks of dengue, as discussed earlier. This will be elaborated upon later in the paper.
To determine when the number of new cases begins to diminish, we use the following approximate threshold [Reference Coutinho10]:
 $$\eqalign{Th(t) & = \displaystyle{{\phi a_1a_2bc} \over {\mu _M(\mu _H + \gamma _H + \alpha _H)}}\displaystyle{{M_S(t)} \over {N_H(t)}}\displaystyle{{H_S(t)} \over {N_H(t)}} \cr & = R_0\displaystyle{{M_S(t)} \over {N_H(t)}}\displaystyle{{H_S(t)} \over {N_H(t)}}\displaystyle{{N_H\left( 0 \right)} \over {N_M\left( 0 \right)}}.}$$
$$\eqalign{Th(t) & = \displaystyle{{\phi a_1a_2bc} \over {\mu _M(\mu _H + \gamma _H + \alpha _H)}}\displaystyle{{M_S(t)} \over {N_H(t)}}\displaystyle{{H_S(t)} \over {N_H(t)}} \cr & = R_0\displaystyle{{M_S(t)} \over {N_H(t)}}\displaystyle{{H_S(t)} \over {N_H(t)}}\displaystyle{{N_H\left( 0 \right)} \over {N_M\left( 0 \right)}}.}$$
When R(t) crosses one from above (below), the incidence and prevalence reach a maximum (minimum). We consider only the first outbreak, namely the only one that has physical meaning.
It is important to note three things:
-
(1) If nothing changes in the neighbourhood that we are studying, then when the threshold, Th(t), is reached, the outbreak is interrupted and the infection rapidly disappears. The number of residual susceptible individuals, H′ S , results in a new R 0 that we call R 0b = R 0 H′ S /N H , which is <1 in the following year. Therefore, no outbreak is expected with a likelihood that is numerically equal to this new R 0b (see discussion below). Conversely, if something changes during the outbreak (heavy rain, public health interventions, drought, etc.), then the threshold may be reached, for example by variation of the factor M S (t)/N H (t) in equation (5). In this case, the remaining number of susceptible individuals is large enough, and we expect another outbreak in the following year because the population of mosquitoes increases very rapidly (see discussion below).
-
(2) The number of cases predicted by the model, if nothing changes, is much larger than the number of cases actually observed and reported in all dengue outbreaks of which we are aware. This appears strange because the parameters used in the model are obtained empirically; an explanation for this will be given later.
-
(3) The total number of cases in the first outbreak predicted by this simple model increases with the two components of R 0 [Reference Ball11, Reference Massad12]:
(6) $$T_{H \to M} = \displaystyle{{N_Va_2c} \over {N_H\left( {\gamma _H + \mu _H + \alpha _H} \right)}},$$
(7)
$$T_{H \to M} = \displaystyle{{N_Va_2c} \over {N_H\left( {\gamma _H + \mu _H + \alpha _H} \right)}},$$
(7) $$T_{M \to H} = \displaystyle{{a_1b\phi} \over {\mu _M}},$$
$$T_{M \to H} = \displaystyle{{a_1b\phi} \over {\mu _M}},$$
with
as shown in Table 2.
Table 2. Percentage of (a) infected individuals, (b) latent mosquitoes, and (c) infected mosquitoes in the first outbreak
The epidemics for a large R 0 eventually saturate the population; in other words, the proportion of infected people approaches 1, as shown in Figure 2.

Fig. 2. Proportion of infected individuals in the first outbreak as a function of T H→M and T M→H .
This result implies that for large values of R 0, which is the product of T H→M and T M→H , it is very unlikely that the infection will return in the subsequent year after the outbreak. We will return to this point later in the paper.
Simulating some observed patterns of dengue recurrence
The epidemic patterns (time distribution of yearly incidence of the infection) in many cities in Brazil are extremely complicated. However, the model given by the system of equation (1) can be used to fit any observed pattern. In the Results section, we show two examples of such a fitting for two different cities with completely different patterns: Natal and Recife (both in northeast Brazil)
We now explain how this can be accomplished. As stated above, the classical Ross–Macdonald model, which is only one population of humans and one population of mosquitoes with R 0 > 1, produces a large outbreak followed by smaller blips of infection that are widely separated in time (typically decades) and are, therefore, non-physical. This large outbreak occurs because, as noted by Amaku et al. [Reference Amaku6], this equation is solved by assuming an initial population of infected individuals uniformly distributed over the region is being studied. Therefore, the disease occurs simultaneously everywhere in the area and produces a single very large outbreak, as shown in Figure 3. After this peak, the infection dies out, which means that the number of cases falls to zero and remains close to zero for several years. This happens when the threshold [Reference Coutinho10] is reached, which occurs even when R 0 is only slightly >1.
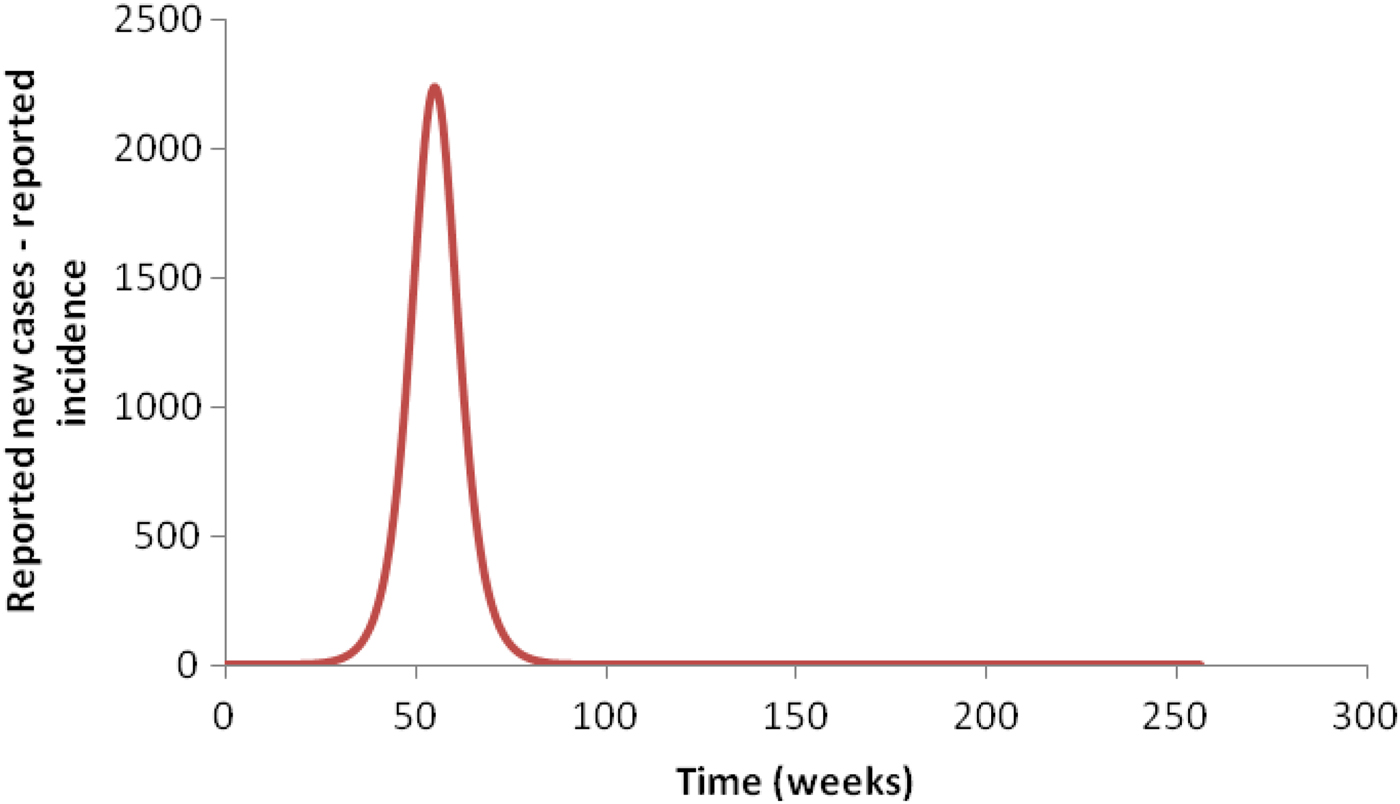
Fig. 3. Simulation of an outbreak when the initial condition is spread throughout the area: a single large peak is obtained.
As mentioned above, however, other factors may cause Th(t) to fall <1. For instance, factors affecting survival of the mosquitoes, such as heavy rain, drought, sanitary interventions and cold weather, may result in Th(t) < 1. As a consequence, it is possible to have a residual
![]() $H^{\prime}_S(t)/N_H(t)$
after an outbreak that is large enough to guarantee an outbreak in the following year. However, due to smaller density of mosquitoes, the outbreak may not occur. To summarize, if external factors do not interfere with the intensity of transmission, the outbreak is interrupted by the lack of enough susceptible individuals to maintain it. In such a case, we will have a residual
$H^{\prime}_S(t)/N_H(t)$
after an outbreak that is large enough to guarantee an outbreak in the following year. However, due to smaller density of mosquitoes, the outbreak may not occur. To summarize, if external factors do not interfere with the intensity of transmission, the outbreak is interrupted by the lack of enough susceptible individuals to maintain it. In such a case, we will have a residual
![]() $H^{\prime}_S(t)/N_H(t)$
low enough that an outbreak in the following year is rendered unlikely. If, however, the outbreak is interrupted by external factors before
$H^{\prime}_S(t)/N_H(t)$
low enough that an outbreak in the following year is rendered unlikely. If, however, the outbreak is interrupted by external factors before
![]() $H^{\prime}_S(t)/N_H(t)$
is low enough, then the new R
0b
will be >1, and an outbreak in the following year may occur. The size of the new outbreak will be dependent on the number of susceptible individuals available to be infected and may be larger or smaller than the first outbreak.
$H^{\prime}_S(t)/N_H(t)$
is low enough, then the new R
0b
will be >1, and an outbreak in the following year may occur. The size of the new outbreak will be dependent on the number of susceptible individuals available to be infected and may be larger or smaller than the first outbreak.
If we subdivide the populations into several sub-populations and introduce the disease in just one of them, then we have as many peaks as the number of sub-populations. In this case, the total population is referred to as a ‘meta-population’ in the literature [Reference Ball11]. Figure 4 illustrates the pattern obtained with three identical sub-populations.

Fig. 4. Simulated pattern obtained with three identical sub-populations geographically separated. The infection was introduced in the first sub-population and propagated to the others.
Introducing seasonality completely changes the pattern in Figure 4, as illustrated in Figure 5.
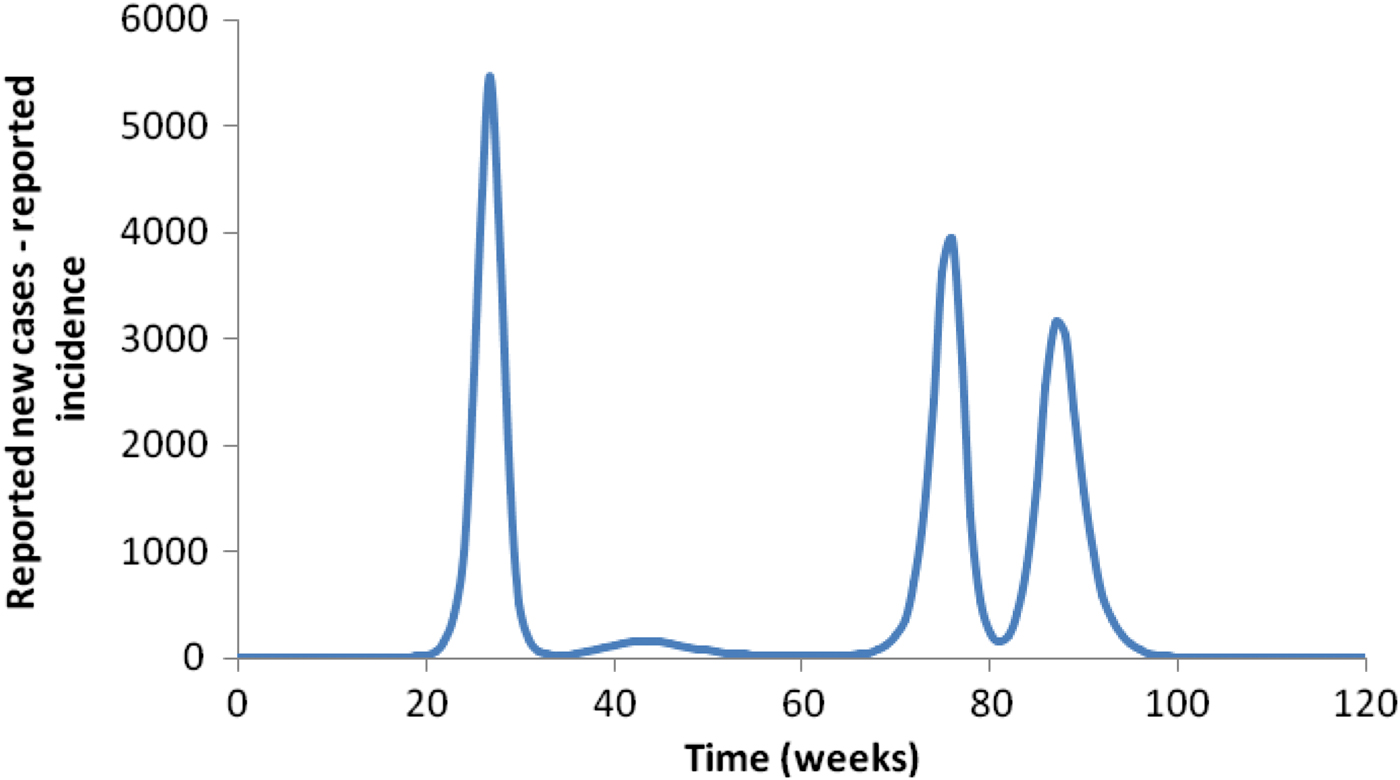
Fig. 5. The effect of seasonality on the pattern shown in Figure 4.
An important observation: invariance of the total number of cases after the first outbreak
It is important to note that the total number of cases is independent of the pattern of outbreaks (time distribution of incidence of cases) if there is no seasonality. Instead, it depends on the values of the parameter that determine the intensity of transmission at the beginning of the epidemic. In fact, the number of cases in the single outbreak produced by the simple Ross–Macdonald model is almost the same as the total number of cases resulting from summing the three peaks in the case illustrated by Figure 4. A small difference occurs because the single peak of the Ross–Macdonald model has a small duration of time, whereas in the other cases, the outbreaks last for a few years and, therefore, demographic effects (people are born and die) take place in between. Obviously, when the mortality and birth rates are negligible, the total number of cases in the first and only outbreak is independent of the pattern of dengue recurrence.
However, when the basic reproduction number is too low (only slightly >1), although the threshold given by equation (5) is reached, the number of remaining susceptible individuals after the outbreak may be large (see Fig. 2).
Effect of seasonality
When seasonality is considered, the total number of mosquitoes is no longer constant and can vary considerably over the course of the year. In Figure 5, we introduced seasonality to modify the patterns shown in Figure 4. The total number of cases after 3 years of simulation is significantly higher than when seasonality is not considered. The total number of cases depends on the time of the year that the infection is ‘introduced’. In Figure 6, we show the variation in the number of cases as a function of the moment the infection is introduced for four different mosquito:human ratios at time t = 0. In the figure, the dotted lines represent the averages around which the number of cases oscillate.

Fig. 6. The effect of seasonality on the total number of cases for four mosquito:human ratios at time t = 0. The mosquito:human ratio varied from a minimum of 0·3 to a maximum of 8·0 over the year due to seasonal variation in the mosquito population size. The continuous lines represent the total number of cases when seasonality is considered. They oscillate around the averages (dotted lines) depending on the time the infection is ‘introduced’.
Although we do not know for certain whether there is any preferential moment for the infection to be introduced in a non-affected area by an infected individual, it is expected that there is a higher probability of introduction during periods of higher infection incidence. Note that the number of cases depends on this moment, which is sufficient to influence the number of cases if the number of susceptible individuals is high enough (above the threshold).
Asymptomatic cases: dark matter
Using the accepted values for the parameters that enter the Ross–Macdonald model for dengue, we always obtain a number of infections that is much greater than what has been reported in any endemic area [Reference Bhatt4]. In this paper, we assume that a proportion of those cases is either not identified or not notified, or both, as dengue cases (these unidentified cases correspond to asymptomatic or undiagnosed acute febrile cases). This proportion varies in the literature from 1:3 to 1:13 [Reference Bhatt4, Reference Chastel13]. We call these unreported/unidentified cases ‘dark matter’, to use the jargon of cosmologists. In the examples that follow, we calculate this proportion in some locations. Unfortunately, we have only one place in Brazil where both seroprevalence data and reported cases of dengue exist [Reference Braga14].
More than one strain of dengue virus or different viruses (Chikungunya, Zika, Yellow fever, etc.)
If there is a super-infection by other dengue strains of viruses in either humans or mosquitoes, there are two distinct possibilities: (1) no competition exists between strains or viruses or (2) competition between strains or viruses does exist. In the former case, each outbreak can be treated separately. For example, if Zika virus does not compete with dengue or other viruses, then we can predict that the outbreak of Zika will be very similar to the outbreak of dengue in the same region. In the second case, an entirely new calculation has to be performed. A possible mechanism for competition can be found in [Reference Burattini, Coutinho and Massad15] and [Reference Amaku16] and will be used in a future paper.
RESULTS: UNDERSTANDING THE DENGUE OSCILLATOR
The main qualitative results of this paper are the following.
An outbreak in a limited district
If the number of mosquitoes in an area of a certain district is such that the R 0 of this area is >1, the disease may invade and an outbreak will occur. In this case, the incidence of the disease will increase until the proportion of susceptible individuals in the host population decreases to a certain level, approximately given by Coutinho et al. [Reference Coutinho10]:
Then, the outbreak will decrease and disappear from this district for a number of years. Immediately after the outbreak, the proportion of remaining susceptible individuals can be calculated as 1 minus the values shown in Table 2a .
Conversely, if for some reason after the outbreak the new R 0b is increased by at least a factor of N Hi/H Si , then another outbreak may occur. In this case, depending on the remaining proportion of susceptible individuals and the new R 0b , the number of individuals affected by the new outbreak may be larger or smaller than the first outbreak, and the number of resistant individuals will approach saturation.
The important point is that, when the R 0 of this area is sufficiently >1, the total number of cases in humans turns out to be independent of variations in the transmission components T H→M and T M→H , provided their values are not significantly altered. For example, if the mosquito density with respect to humans is lower in one district than in the other, then the outbreak will take more time to disappear, but the number of cases will be smaller (see Table 2a ). Note that any outbreak occurring afterwards will depend on the increase of the new R 0b after the outbreak.
Using these results, we can attempt to make certain predictions at a certain point during the epidemic about what will happen in the near future. To illustrate, suppose we have a given district with an intensity of transmission, such that R 0b for this district is >1. Then, we are able to calculate what the number of cases reported in this district at the end of the outbreak will be. If at some point during the epidemic, the total number of cases is above a certain threshold, we can say that the epidemic is over, or, with great probability, if it will continue over time and how many more cases will occur.
Examples of the calculation
The calculation reported below follow these steps:
-
(a) Looking at the data, we tentatively identify epidemics that presumably were interrupted because they reached the threshold given by equation (5). These epidemics are identified by long periods of very low dengue activity between two successive outbreaks.
-
(b) The epidemics may consist of outbreaks that last a few years, but if they recur for more than five consecutive years, the calculation described below breaks down.
-
(c) The calculation assumes a proportion (1 – η) of dark matter and that the epidemic is considered over when the number of susceptible individuals falls below a certain threshold [equation (5)]. Of course, η, the proportion of notified cases, should be confirmed by actual observations. However, the examples below seem to indicate that for a given geographical region, the value of η does not vary very much from place to place.
A single outbreak: the case of the Recife dengue outbreak, 2001–2002
This outbreak consisted of only one peak of cases followed by several years with only marginal dengue transmission. We can therefore tentatively assume that the number of susceptible individuals fell to a level that interrupted the transmission due to herd immunity. In Figure 7, we fitted this outbreak, calculated the total number of cases and discovered that by only by assuming a value of 1:24 for the proportion of dark matter, we recovered the notification data.
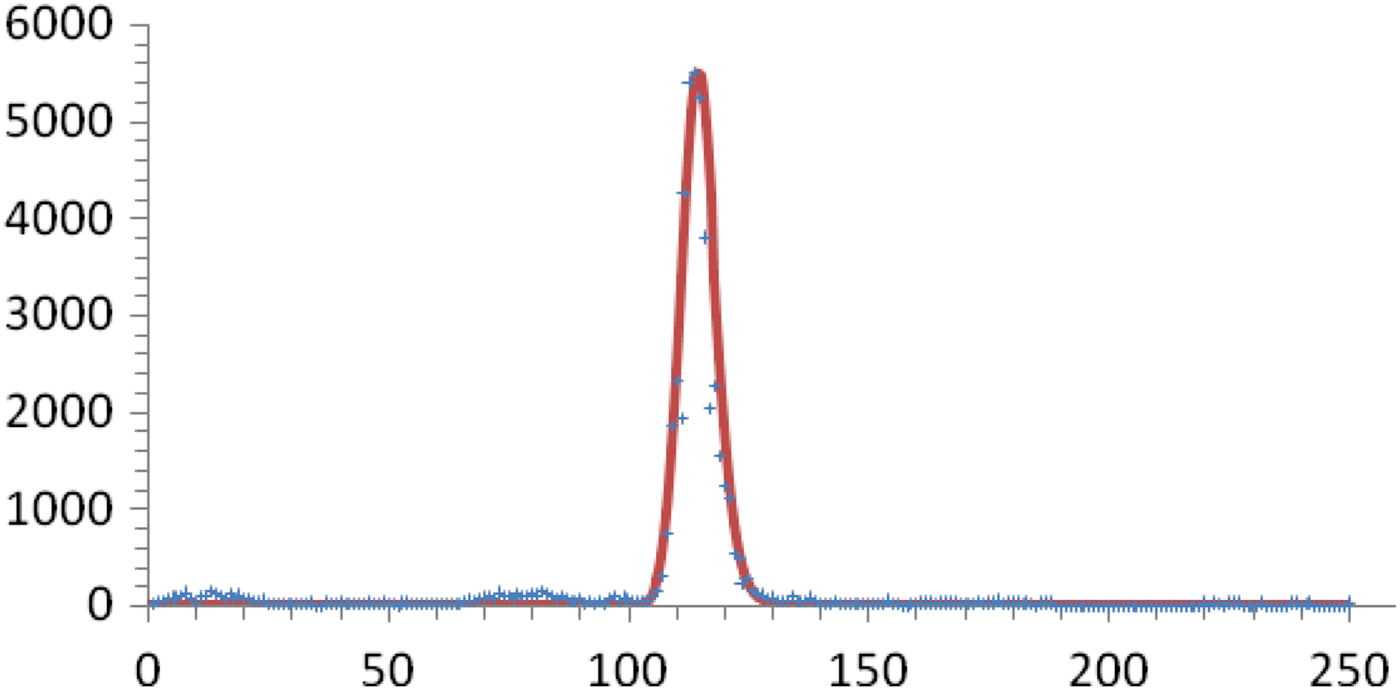
Fig. 7. Number of weekly real (crosses) and calculated (continuous line) reported cases for the 2001–2002 outbreak in Recife, Brazil. The total number of notified cases was 48 500. The total number of cases given by the model, considering η = 0·04, is 1 260 000.
This enormous number of cases represents more than 85% of the total Recife population at the time, indicating that the threshold was reached. Incidentally, it could be predicted that this particular strain of dengue virus would take some time to return, which in fact is what happened. On the other hand, this proportion agrees with the survey carried out by Braga et al. [Reference Braga14] and had a herd immunity corresponding to R 0 > 4.
Multiple outbreaks: the case of the Natal dengue outbreak, 2000–2007
In contrast to the single Recife outbreak described above, dengue in Natal during the period between 2000 and 2007 presented a recurrent pattern with annual outbreaks of smaller magnitude. This pattern was reproduced by the model using nine geographical regions (neighbourhoods) and by assuming that the infection propagates through the movement of infected human hosts in those regions [see equation (1)]. The period between weeks 200 and 330 was fitted by reducing the mosquito density (Fig. 8). Of course, there are other mechanisms that could be used to fit this pattern. The important point is that the number of asymptomatic cases (dark matter) added to the reported cases is greater than the total population in Natal. This can be explained by the fact that there is more than one strain of dengue virus circulating and that the population increased 1% per year during the period. We shall return to this point later in the paper.

Fig. 8. Simulation of the outbreaks in Natal, NE Brazil.
Forecasting outbreaks in a small neighbourhood
Next, we consider a small homogeneous neighbourhood. To predict outbreaks and their intensity, we need basically three quantities: transmission components T H→M and T M→H of the neighbourhood and the value of η, which gives the proportion of dark matter (asymptomatic cases). The challenge is how to measure or estimate these three quantities. Assume we have a neighbourhood where an outbreak occurred and faded away for a few consecutive years – we can then proceed in the following way. We can compare the fraction of reported cases with the fraction predicted by the model in Table 1. If the outbreak occurred a number of years ago, it is safe to consider that the value of η is large. Assuming several η's, we can calculate the likelihood of another outbreak and its magnitude.
Unfortunately, the value of η must be measured, and that may be expensive. However, we can assume several values of η and calculate the corresponding R 0 that explains each η. The value of R 0 can also be calculated by another method; then, the value of η can be deduced.
Even when the outbreak saturates a given neighbourhood of a city, new outbreaks of dengue may be reported in the same city. These outbreaks occur in other neighbourhoods due to the movement of people. In the next section, we examine this problem.
Forecasting outbreaks in large cities
Example 1 São Paulo (Brazil), 2014–2015.
In this case, due to human movement, there are a number of peaks before the entire outbreak fades out. Of course, we have to fit the patterns by considering the different neighbourhoods; however, to make predictions, it is necessary to know in which neighbourhood a particular outbreak occurs. If this is known, then the calculation described in the previous sub-section can be carried out for each region. However, if the city is very large, the outbreaks may be restricted to certain boroughs. In this case, we have to consider the population in the neighbourhoods that are not affected in order to calculate the total number of cases that may occur in the future. Unfortunately, without further information, it is impossible to predict the order of the outbreaks in time and space. We will illustrate this situation with an extreme case, namely the 2013, 2014 and 2015 dengue outbreaks in the megalopolis of São Paulo (Brazil), where we can see that the outbreaks ‘travel’ from place to place in subsequent years (Fig. 9).
Example 2 Rio de Janeiro (Brazil) 2000, 2008 and 2011–2013.
In this example, we illustrate several features of the model.

Fig. 9. Evolution of the dengue outbreak in São Paulo. The situation at the end of (a) 2013, (b) 2014, (c) 2015. The colours represent the number of cases per 100 000 inhabitants.
Rio de Janeiro had three outbreaks which occurred during 2000, 2008 and 2011–2013, respectively. The two epidemics in 2000 and 2008 consisted essentially of two large peaks. We assume, based on some data, that the 2000 outbreak was essentially due to serotype 3, and the 2008 outbreak was mainly due to serotype 2. The three outbreaks in 2011–2013 are assumed to be serotypes 4 and 1 simultaneously.
The sum of the reported cases can be observed in Figure 10. It shows that:
-
(1) The outbreaks show different slopes in several parts before reaching a plateau. This can be interpreted as the epidemic moving through the city.
-
(2) The outbreaks of 2000 and 2008 reached approximately the same number of cases. From this we can deduce a value for η.
-
(3) The outbreaks of 2011–2013 did not reach the entire city. In Figure 11(a,b), shows the accumulated number of cases for two different districts of Rio, namely, Ilha do Governador and Centro.
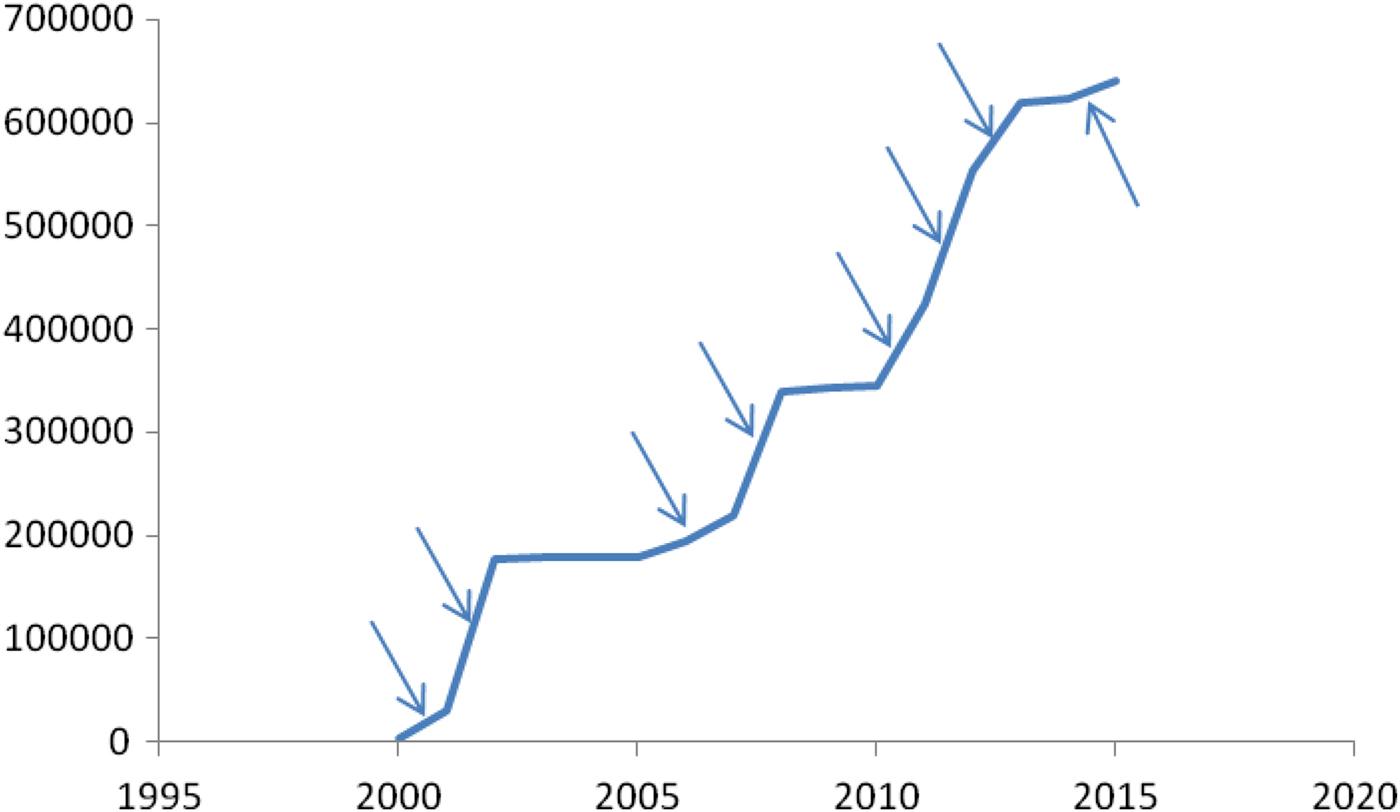
Fig. 10. Accumulated reported cases in Rio de Janeiro (Brazil), 2000–2015.

Fig. 11. (a) Accumulated number of dengue cases in the Ilha do Governador borough. Arrows indicate the epidemic spreading to other regions of the borough. The outbreaks of 2011–2013 are approximately double that of the previous outbreaks. This indicates that there were two strains circulating. (b) The number of accumulated dengue cases in the central region of Rio de Janeiro. Arrows indicate the epidemic spreading to other regions of the borough. Note that in this case, the outbreaks of 2011–2013 are approximately of the same magnitude as those of previous outbreaks. This indicates that there was only one strain circulating in this region.
FORECASTING
Forecasting outbreaks in large cities, as we have shown above, may be very difficult. We recapitulate the reasons for this:
-
(a) When an epidemic enters a large city, it will enter into a small neighbourhood and then propagate to the rest of the city. This movement can lead to peaks in the same city for 3–4 years before the epidemic fades out, which occurs when the condition given by equation (5) reaches 1 everywhere in the city.
-
(b) Large cities are rarely homogeneous; therefore, the interruption of epidemics may occur with different proportions of immune people in different parts of the city.
-
(c) Even in a given neighbourhood, as explained previously, the epidemic can be interrupted by climatic factors. If this happens, there will be a number of peaks until the threshold given by equation (5) crosses one downwards from above, and then the infection disappears.
Therefore, to predict epidemics in large cities, proceed as follows:
-
(1) Choose a well-described past outbreak and divide the city into homogeneous regions with respect to the number of cases observed, or better, with respect to the proportion of remaining susceptible individuals at the end of the outbreak.
-
(2) For each region, calculate the remaining number of susceptible individuals. The difficulty here is to know the exact number of subclinical infections. If this is known, then the total number of cases can be adjusted.
-
(3) If the number of subclinical infections is not known, then neighbourhoods free from infection for a few years must be selected. Therefore:
-
• assume values of η, and calculate R 0 for these regions. Of course, the value of η cannot be too large because we would end up with more people infected than the total population;
-
• given the population size of this region, the maximum value of R 0 can be calculated for this particular region;
-
• for each R 0 the likelihood of an outbreak in the following year and its maximum size can be estimated.
-
SUMMARY AND CONCLUSIONS
For several years, the number of dengue cases in a city (or in a borough of a city) has been reported weekly for the entire country. The reported data form a time series and show the annual outbreaks (sometimes more than one outbreak in a single year) with a very irregular nature. As mentioned before, we call these series the dengue oscillator.
The purpose of this paper is to explain these outbreaks from a semi-quantitative point of view. Towards that end, we used the classical Ross–Macdonald model. This model, as usually formulated, predicts a large outbreak followed by smaller outbreaks that occur decades later and is clearly unrealistic. The reason why the model is unrealistic when it is naively applied is that the initial conditions assume that the infection enters the city or borough uniformly, as noted by Amaku et al. [Reference Amaku6]. The model also predicts a much larger number of cases than are actually observed, although it uses measured parameters. In this paper, we show that by dividing the population into small areas, introducing the infection in just one area (or in just a few), and introducing seasonality we are able to reproduce any pattern observed. The true vector of dengue is the human host who carries the infection around the city. The large number of cases is explained by the asymptomatic cases that range from factor 4 to factor 13 with respect to the symptomatic cases. It may appear that we have unfairly criticized the classical Ross–Macdonald model – this is not the case. In fact we show, in this paper, that the classical Ross–Macdonald model, if properly applied, can explain the patterns of outbreaks observed in real-world settings. The basic trick was to divide the whole population into sub-populations and/or to introduce seasonal variations. A price had to be paid since a number of new parameters had to be introduced. However, one of the major findings of this paper was that no matter how complex the patterns of outbreaks are, the final total number of cases was the same that would be obtained by using the simple version of the Ross–Macdonald model. The classical Ross–Macdonald model was modified by introducing spatial heterogeneities and seasonality. This is sufficient to explain any patterns observed so far. Other heterogeneities like age-dependent biting preferences by the mosquitoes, human differential susceptibility, etc., might complicate the model so much that the qualitative insights provided by this simpler version could be compromised.
Understanding the mechanism of dengue transmission is the first step to forecasting future outbreaks.
The methods described in this paper allow other types of inferences. For instance, if in a given year, the number of cases is far too high to be explained by the dengue mechanisms explained above, it can be suspected that another virus was introduced into the population. This may either be another strain of dengue or, as we suspected, a new infection such as Zika virus (see Fig. 10).
Finally, a word of caution related to the values of the parameters used in this paper. It is true that, on the one hand, the assignment of values to parameters borrowed from the literature is a practice that does not have any statistical ground. On the other hand, however, the parameters necessary to run the model are relatively well known from many decades of entomological studies (about this, we included in the new version the phrase which values are accepted from the literature). Consider, for instance, the biting rate of mosquitoes. This parameter has physical limits well established for Ae. aegypti and varies from 0 to 3 bites per day, on average. Although we used the average value of 1 bite per day, even changing this value would not alter the qualitative behaviour of the model too much. The same comment is valid for the demographic parameters of mosquitoes and hosts, the probabilities of mosquito infections from infective hosts, and the probability of host infections from infective mosquitoes, and the parameters related to dengue disease (duration of infection and mortality rates). The new parameters introduced in this paper, the proportion of individuals from neighbourhood i that visit neighbourhood j,
![]() $\beta _{ij}^H $
, and the proportion of mosquitoes from neighbourhood i that bite humans from neighborhood j,
$\beta _{ij}^H $
, and the proportion of mosquitoes from neighbourhood i that bite humans from neighborhood j,
![]() $\beta _{ij}^M $
, are, however, variable from place to place and are almost impossible to be estimated with any statistical significance. In addition, the aims of our work can be summarized as follows: to understand dengue oscillatory and recurrent patterns; to propose a model to explain qualitatively those patterns; and to identify which variables and parameters need to be known to help in outbreak prediction. Note that the current paper is not intended to provide tools for decision making but rather to understand dengue oscillatory behaviour. The part of the paper related to forecasting, however, uses reported numbers of cases and does not depend on fine details of the components of the model, at least not from the formal statistical point of view.
$\beta _{ij}^M $
, are, however, variable from place to place and are almost impossible to be estimated with any statistical significance. In addition, the aims of our work can be summarized as follows: to understand dengue oscillatory and recurrent patterns; to propose a model to explain qualitatively those patterns; and to identify which variables and parameters need to be known to help in outbreak prediction. Note that the current paper is not intended to provide tools for decision making but rather to understand dengue oscillatory behaviour. The part of the paper related to forecasting, however, uses reported numbers of cases and does not depend on fine details of the components of the model, at least not from the formal statistical point of view.
ACKNOWLEDGEMENTS
This work was partially supported by LIM01 HCFMUSP, Fapesp (2014/26229-7 and 2014/26327-9), CNPq, Dengue Tools under the Seventh Framework Programme of the European Community, grant agreement no. 282589, and MS/ FNS (grant no. 777588/2012).
DECLARATION OF INTEREST
None.


















