INTRODUCTION
The purpose of this paper is to examine the role of mathematical models in evaluating control strategies for diseases, illuminating their limitations and possible errors that can occur if these limitations are not carefully considered.
For diseases involving vectors, the number of variables can be large and it is sometimes unnecessary and misleading to use all the complexities of the real biological system.
As noted by Mazilu et al. [Reference Mazilu, Zamora and Mazilu1], this is far from a trivial matter: ‘Building simple models that capture the essence of a physical phenomenon is not an easy task: there is a fine line between an accurate model that is as simple as possible, and an unrealistic model.’
This paper is arranged in three main sections.
In the following section (General considerations about modelling vector-borne infections), we show how, considering the purpose of the model, we can simplify the description of a complicated system as a vector-borne disease. We then illustrate how to limit the model variables according to our needs. In so doing, we aim to explain why there are many models of the same (or similar) systems with different numbers of variables [Reference Ross2–Reference Coutinho4].
The next section (Estimating R 0 from the initial growing phase of an outbreak: several pitfalls), examines one example found in a recent paper [Reference Pinho5] that illustrates the dangers of basing control strategies on models without considering their limitations. We show that the method used cannot be applied as done by the authors, and that as a consequence, some of the conclusions reached are not correct. Unfortunately, the incorrect results, if taken as true by public health authorities, would greatly harm the affected populations and the reputation of the use of models in this field.
Finally, in the ‘Backward bifurcation’ section, we review an interesting paper by Garba et al. [Reference Garba, Gumel and Abu Bakar6] that contains some biological assumptions that are inappropriate for dengue but may apply to other vector-borne infections. In addition, it contains some algebraic misprints that make it difficult to read. The paper's conclusion is that a backward bifurcation exists in the system; this is examined in our paper from a different point of view. Furthermore, the conclusions of Garba et al., which do not apply to dengue, would make the control of even those diseases to which Garba's parameters do apply extremely difficult. We argue that the values of the biological parameters used by Garba et al. are not realistic for dengue.
We will show in the ‘Estimating R 0 …’ section that the variables in the equations of the models are densities, i.e. vectors/humans per unit area. Therefore, if these densities are spatially homogeneous and the area investigated is small, total numbers can be obtained by multiplying the variables by the area of the region under consideration. However, when we investigate the outbreak of an epidemic, we should consider that the initial infection is not distributed homogeneously throughout the area under consideration. In the literature, this is often disregarded and epidemics are investigated by assuming that the disease invades an area homogeneously. In Appendix I, we show the effects of the initial distribution of the disease on the size and duration of the epidemic.
GENERAL CONSIDERATIONS ABOUT MODELLING VECTOR-BORNE INFECTIONS
We will use dengue as an example of a vector-borne disease to illustrate points that are also valid for other vector-borne diseases, such as malaria and yellow fever. We do this to simplify the notation and make the points we want to emphasize simpler to understand.
In the dengue system, there are several populations involved: a human population, an adult mosquito population, at least six aquatic forms and mosquito eggs. In addition, there is the virus, which in dengue's case will be one of four known serotypes.
Our first point is the question of how to choose the populations that will enter the model. In the seminal papers by Ross [Reference Ross2] and Macdonald [Reference Macdonald3] (that address malaria), only adult mosquitoes, humans and parasites were considered. This was because they wanted to investigate the existence of critical sizes of these populations, below which the disease would disappear. In the mathematical literature, a model exhibiting this feature is said to have a threshold and, in the case of diseases, this threshold is given by the well-known basic reproduction number, R 0 [Reference Anderson and May7]. Let us briefly recall a slightly generalized form of the classical Ross–Macdonald model [Reference Ross2, Reference Macdonald3]. The variables are described in Table 1 and are usually denoted as ‘compartments’ of the model.
Table 1. Variables of the model and their biological description

The equations that govern the dynamics of the system are given below and explained immediately afterwards.
 $$\left.\eqalign{\displaystyle{ {d{S_H}} \over {dt}} = & - ab({I_M} + {\eta _M}{L_M})\displaystyle{{{S_H}} \over {{N_H}}} - {\mu _H}{S_H} + {\sigma _H}{R_H} \cr&+ {\theta _H}{I_H} + {\Lambda _H}\comma \cr \displaystyle{{d{L_H}} \over {dt}} = & \;ab({I_M} + {\eta _M}{L_M})\displaystyle{{{S_H}} \over {{N_H}}} - ({\mu _H} + {\delta _H}){L_H}\comma \cr \displaystyle{{d{I_H}} \over {dt}} = & \;{\delta _H}{L_H} - ({\mu _H} + {\alpha _H} + {\gamma _H} + {\theta _H}){I_H}\comma \cr \displaystyle{{d{R_H}} \over {dt}} = & \;{\gamma _H}{I_H} - ({\mu _H} + {\sigma _H}){R_H}\comma\cr \displaystyle{{d{S_M}} \over {dt}} = & - ac\displaystyle{{({I_H} + {\eta _H}{L_H})} \over {{N_H}}}{S_M} - {\mu _M}{S_M} + {\Lambda _M}\comma \cr \displaystyle{{d{L_M}} \over {dt}} = & \;ac\displaystyle{{({I_H} + {\eta _H}{L_H})} \over {{N_H}}}{S_M} - ({\mu _M} + {\gamma _M}){L_M}\comma \cr \displaystyle{{d{I_M}} \over {dt}} = & \;{\gamma _M}{L_M} - {\mu _M}{I_M}.}\right\}$$
$$\left.\eqalign{\displaystyle{ {d{S_H}} \over {dt}} = & - ab({I_M} + {\eta _M}{L_M})\displaystyle{{{S_H}} \over {{N_H}}} - {\mu _H}{S_H} + {\sigma _H}{R_H} \cr&+ {\theta _H}{I_H} + {\Lambda _H}\comma \cr \displaystyle{{d{L_H}} \over {dt}} = & \;ab({I_M} + {\eta _M}{L_M})\displaystyle{{{S_H}} \over {{N_H}}} - ({\mu _H} + {\delta _H}){L_H}\comma \cr \displaystyle{{d{I_H}} \over {dt}} = & \;{\delta _H}{L_H} - ({\mu _H} + {\alpha _H} + {\gamma _H} + {\theta _H}){I_H}\comma \cr \displaystyle{{d{R_H}} \over {dt}} = & \;{\gamma _H}{I_H} - ({\mu _H} + {\sigma _H}){R_H}\comma\cr \displaystyle{{d{S_M}} \over {dt}} = & - ac\displaystyle{{({I_H} + {\eta _H}{L_H})} \over {{N_H}}}{S_M} - {\mu _M}{S_M} + {\Lambda _M}\comma \cr \displaystyle{{d{L_M}} \over {dt}} = & \;ac\displaystyle{{({I_H} + {\eta _H}{L_H})} \over {{N_H}}}{S_M} - ({\mu _M} + {\gamma _M}){L_M}\comma \cr \displaystyle{{d{I_M}} \over {dt}} = & \;{\gamma _M}{L_M} - {\mu _M}{I_M}.}\right\}$$
The model parameters and their biological interpretation are given in Table 2.
Table 2. Model parameters and their biological interpretation

Let us explain the meaning and limitations of the above model. First, as explained, the variables are densities, i.e. the number of humans/vectors per unit area. Therefore, to use the model as it is written above, we should consider an area where the population is approximately homogenously distributed and multiply each variable by this area. A qualitatively comprehensive attempt to discuss the challenge of calculating parameters taking into account spatial heterogeneities can be found in [Reference Riley8]. One particularly important point is raised by the term
Let us explain the meaning of this term. The parameter a is a composed quantity. Let a be the area explored by a mosquito via the joint movement of humans and mosquitoes. Let ξ be the number of bites a mosquito inflicts per unit time and per unit area in the human population. Then, ξ AI M is the number of bites that AI M infected mosquitoes inflict on N H A people. Hence, the fraction of bites inflicted on susceptible humans is ξAI M (S H A/NHA) = αI M (S H /NH ), where
Therefore, the number of susceptible humans that acquire the infection from infected mosquitoes per unit time is abI M (S H /N H ), where b is the probability that a bite from an infected mosquito results in an infected (latent) human. Assuming that latent mosquitoes also transmit the infection, although with a lower probability, expressed by η M , we see that equation (2) represents the density of new infections per unit time due to mosquito bites.
Analogously, the term
![]() $ac{\textstyle{{({I_H} + {\eta _H}{L_H})} \over {{N_H}}}}{S_M}$
represents the density of new infections per unit time in mosquitoes due to mosquito bites on infective humans.
$ac{\textstyle{{({I_H} + {\eta _H}{L_H})} \over {{N_H}}}}{S_M}$
represents the density of new infections per unit time in mosquitoes due to mosquito bites on infective humans.
The two quantities Λ
H
and Λ
M
are the number of humans and vectors born or otherwise introduced per unit area per unit time into the susceptible compartments. It is usual to assume that Λ
H
is a logistic term of the type
![]() ${r_H}{N_H}(1 - {\textstyle{{{N_H}} \over {{K_H}}}})$
, where r
H
is the Malthusian parameter and K
H
is the carrying capacity. Analogously, Λ
M
is the quantity of vectors that are born or otherwise introduced per unit area per unit time.
${r_H}{N_H}(1 - {\textstyle{{{N_H}} \over {{K_H}}}})$
, where r
H
is the Malthusian parameter and K
H
is the carrying capacity. Analogously, Λ
M
is the quantity of vectors that are born or otherwise introduced per unit area per unit time.
The other terms are transition terms between the compartments as explained, for example, in [Reference Lopez9].
From equation (1), we can deduce [Reference Coutinho4, Reference Lopez9, Reference Amaku10] that the disease cannot invade the host population if R 0 is <1, where R 0 is
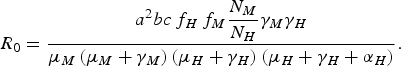 $${R_0} = \displaystyle{{{a^2}bc{\,f_H}{\,f_M}\displaystyle{{{N_M}} \over {{N_H}}}{\gamma _M}{\gamma _H}} \over {{\mu _M}\left( {{\mu _M} + {\gamma _M}} \right)\left( {{\mu _H} + {\gamma _H}} \right)\left( {{\mu _H} + {\gamma _H} + {\alpha _H}} \right)}}.$$
$${R_0} = \displaystyle{{{a^2}bc{\,f_H}{\,f_M}\displaystyle{{{N_M}} \over {{N_H}}}{\gamma _M}{\gamma _H}} \over {{\mu _M}\left( {{\mu _M} + {\gamma _M}} \right)\left( {{\mu _H} + {\gamma _H}} \right)\left( {{\mu _H} + {\gamma _H} + {\alpha _H}} \right)}}.$$
The terms f H and f M are defined as
In the limit when η M = 0 and δ H →∞, we obtain the expression of R 0 of the original Macdonald model [Reference Macdonald3]:
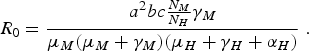 $${R_0} = \displaystyle{{{a^2}bc{\textstyle{{{N_M}} \over {{N_H}}}}{\gamma _M}} \over {{\mu _M}({\mu _M} + {\gamma _M})({\mu _H} + {\gamma _H} + {\alpha _H})}}\;.$$
$${R_0} = \displaystyle{{{a^2}bc{\textstyle{{{N_M}} \over {{N_H}}}}{\gamma _M}} \over {{\mu _M}({\mu _M} + {\gamma _M})({\mu _H} + {\gamma _H} + {\alpha _H})}}\;.$$
The above result is very important because it indicates that we do not have to completely eradicate the mosquito population to prevent the disease from invading the host population [Reference Ross2]. Note, however, that the model is valid only when applied to a region where the populations involved (mosquitoes and humans) are spatially homogeneous, and in any case, border effects were neglected. We shall expand on this later in the paper.
In some regions of the world, seasonality affects the mosquito population considerably and, in some cases, the mosquito density falls so much that transmission is interrupted in the dry season. The disease, however, overwinters and reappears in the next season. A hypothesis to explain this phenomenon is transovarian transmission in the mosquitoes [Reference Coutinho4]. In this case, we are therefore forced to consider in the model the aquatic stages of the vector. Control measures that aim for the destruction of breeding places also force us to include aquatic forms in the model, even if seasonality is negligible. The model described in equation (1) has to be modified to include the immature forms. This can be done by modifying the last three equations related to the vectors in system (1) as follows:
 $$\left.\eqalign{\displaystyle{{d{S_M}} \over {dt}} = & - ac\displaystyle{{({I_H} + {\eta _H}{L_H})} \over {{N_H}}}{S_M} - {\mu _M}{S_M} + {\Lambda _M}\comma \cr \displaystyle{{d{L_M}} \over {dt}} = & \;ac\displaystyle{{({I_H} + {\eta _H}{L_H})} \over {{N_H}}}{S_M} - ({\mu _M} + {\gamma _M}){L_M}\comma \cr \displaystyle{{d{I_M}} \over {dt}} = & \;{\gamma _M}{L_M} - {\mu _M}{I_M}.}\right\} $$
$$\left.\eqalign{\displaystyle{{d{S_M}} \over {dt}} = & - ac\displaystyle{{({I_H} + {\eta _H}{L_H})} \over {{N_H}}}{S_M} - {\mu _M}{S_M} + {\Lambda _M}\comma \cr \displaystyle{{d{L_M}} \over {dt}} = & \;ac\displaystyle{{({I_H} + {\eta _H}{L_H})} \over {{N_H}}}{S_M} - ({\mu _M} + {\gamma _M}){L_M}\comma \cr \displaystyle{{d{I_M}} \over {dt}} = & \;{\gamma _M}{L_M} - {\mu _M}{I_M}.}\right\} $$
First, we introduce two new system variables (compartments) representing non-infected and infected aquatic forms: S E and I E , respectively. For simplicity, we consider all the aquatic forms, i.e. eggs, larvae and pupae, as a single compartment (we use a subscript E to represent eggs). The new system reads
 $$\left.\eqalign{\displaystyle{{d{S_M}} \over {dt}} = & - ac\displaystyle{{({I_H} + {\eta _H}{L_H})} \over {{N_H}}}{S_M} - {\mu _M}{S_M} + p{c_s}(t){S_E}\comma \cr \displaystyle{{d{L_M}} \over {dt}} = & \;ac\displaystyle{{({I_H} + {\eta _H}{L_H})} \over {{N_H}}}{S_M} - ({\mu _M} + {\gamma _M}){L_M}\comma \cr \displaystyle{{d{I_M}} \over {dt}} = &\; {\gamma _M}{L_M} - {\mu _M}{I_M} + p{c_s}(t){I_E} \comma \cr \displaystyle{{d{S_E}} \over {dt}} = &\; [{r_M}{S_M} + (1 - g){r_M}({I_M} + {L_M})]\cr &\times\left( {1 - \displaystyle{{{S_E} + {I_E}} \over {{K_E}}}} \right) - {\mu _E}{S_E} - p{c_s}(t){S_E}\comma \cr \displaystyle{{d{I_E}} \over {dt}} = & \;[g{r_M}({I_M} + {L_M})]\left( {1 - \displaystyle{{{S_E} + {I_E}} \over {{K_E}}}} \right) - {\mu _E}{I_E} \cr &- p{c_s}(t){I_E}.}\right\} $$
$$\left.\eqalign{\displaystyle{{d{S_M}} \over {dt}} = & - ac\displaystyle{{({I_H} + {\eta _H}{L_H})} \over {{N_H}}}{S_M} - {\mu _M}{S_M} + p{c_s}(t){S_E}\comma \cr \displaystyle{{d{L_M}} \over {dt}} = & \;ac\displaystyle{{({I_H} + {\eta _H}{L_H})} \over {{N_H}}}{S_M} - ({\mu _M} + {\gamma _M}){L_M}\comma \cr \displaystyle{{d{I_M}} \over {dt}} = &\; {\gamma _M}{L_M} - {\mu _M}{I_M} + p{c_s}(t){I_E} \comma \cr \displaystyle{{d{S_E}} \over {dt}} = &\; [{r_M}{S_M} + (1 - g){r_M}({I_M} + {L_M})]\cr &\times\left( {1 - \displaystyle{{{S_E} + {I_E}} \over {{K_E}}}} \right) - {\mu _E}{S_E} - p{c_s}(t){S_E}\comma \cr \displaystyle{{d{I_E}} \over {dt}} = & \;[g{r_M}({I_M} + {L_M})]\left( {1 - \displaystyle{{{S_E} + {I_E}} \over {{K_E}}}} \right) - {\mu _E}{I_E} \cr &- p{c_s}(t){I_E}.}\right\} $$
The new parameters in system (7) are described in Table 3.
Table 3. Parameters and their biological meaning in the model with aquatic forms

Let us now describe the meaning of some terms of system (7). The term pc
s
(t)S
E
represents the number of non-infected eggs per unit area per unit time that reach the adult stage. The parameter c
s
(t) was introduced to mimic seasonality (see [Reference Coutinho4]). The term pc
s
(t)I
E
represents the number of infected eggs per unit area per unit time that reach the infected adult stage. The term
![]() $[{r_M}{S_M} + (1 - g){r_M}({I_M} + {L_M})]\left( {1 - {\textstyle{{{S_E} + {I_E}} \over {{K_E}}}}} \right)$
is a logistic-like term that represents the rate of mosquito reproduction in the form of non-infected eggs. Similarly,
$[{r_M}{S_M} + (1 - g){r_M}({I_M} + {L_M})]\left( {1 - {\textstyle{{{S_E} + {I_E}} \over {{K_E}}}}} \right)$
is a logistic-like term that represents the rate of mosquito reproduction in the form of non-infected eggs. Similarly,
![]() $[g{r_M}({I_M} + {L_M})]\left( {1 - {\textstyle{{{S_E} + {I_E}} \over {{K_E}}}}} \right)$
is a logistic-like term that represents the rate of mosquito reproduction in the form of infected eggs. K
E
is the carrying capacity of the environment. The remaining terms are transition rates between the compartments. This modified system also predicts a threshold for the infection to invade the host population (for details, see [Reference Coutinho4]). Note that we assume that the mortality of infected eggs is the same as the mortality of non-infected eggs. This is easily modified but, in the spirit of avoiding unnecessary experimentally unknown facts, we prefer to assume them equal. The proportional distribution of infected eggs into non-infected and infected mosquitoes was briefly discussed in [Reference Coutinho4]. In this reference, it was shown that this parameter is very important to explain semi-quantitatively dengue overwintering.
$[g{r_M}({I_M} + {L_M})]\left( {1 - {\textstyle{{{S_E} + {I_E}} \over {{K_E}}}}} \right)$
is a logistic-like term that represents the rate of mosquito reproduction in the form of infected eggs. K
E
is the carrying capacity of the environment. The remaining terms are transition rates between the compartments. This modified system also predicts a threshold for the infection to invade the host population (for details, see [Reference Coutinho4]). Note that we assume that the mortality of infected eggs is the same as the mortality of non-infected eggs. This is easily modified but, in the spirit of avoiding unnecessary experimentally unknown facts, we prefer to assume them equal. The proportional distribution of infected eggs into non-infected and infected mosquitoes was briefly discussed in [Reference Coutinho4]. In this reference, it was shown that this parameter is very important to explain semi-quantitatively dengue overwintering.
ESTIMATING R 0 FROM THE INITIAL GROWING PHASE OF AN OUTBREAK: SEVERAL PITFALLS
From the discussion in the previous section, we can see that calculating R 0 for a given population is an important task. This can be done in several ways. A simple way first proposed by May & Anderson [Reference May and Anderson11] for directly transmitted infection was adapted by Massad et al. [Reference Massad12] and further refined by Favier et al. [Reference Favier13] for vector-borne infections. The first pitfall we will discuss was the use made by Pinho et al. [Reference Pinho5] of this method as described below.
In their paper, Pinho et al. [Reference Pinho5] analysed the dengue epidemic in Salvador, Brazil, and concluded that
The value of R 0 is greater than 1 for the epidemic in 1995–1996 for any chosen value of the vector-control parameter, indicating that other strategies would be necessary besides the adult vector-control, as such as the control of the mosquito's aquatic phase, to reduce its force of infection and therefore to control the epidemic.
The aim of this section is to show that this conclusion cannot be deduced from either the model they used or from the calculations presented in their paper.
In fact, the equilibrium solutions of the model given by their equations (2.1) can be deduced analytically [Reference Amaku10]. It is also possible, and easier, to deduce two thresholds. The first (denoted ‘basic offspring’ or demographic reproduction number) determines the permanence or extinction of the mosquito population. The second is a variant of the classical Macdonald [Reference Macdonald3] basic reproduction number (R 0) and determines the establishment or extinction of the infection. From these results, and also from numerical simulations of the model, it is easy to see that by increasing the adult mortality rate, μ M , or the aquatic phase mortality rate, μ a , we can reach Macdonald's threshold before reaching the basic offspring threshold. Therefore, the disease dies out without eliminating the mosquito population (see Fig. 1 below from Pinho et al.'s model). Thus, Macdonald's threshold is useful. It would be useless if Pinho et al. [Reference Pinho5, pp. 5692] were correct.

Fig. 1. The values of c M such that the disease dies out but the mosquito population is still present.
The authors reached their conclusion by using their equation (3.8)
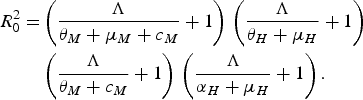 $$\eqalign{R_0^2 = & \left( {\displaystyle{\Lambda \over {{\theta _M} + {\mu _M} + {c_M}}} + 1} \right)\,\left( {\displaystyle{\Lambda \over {{\theta _H} + {\mu _H}}} + 1} \right)\, \cr & \left( {\displaystyle{\Lambda \over {{\theta _M} + {c_M}}} + 1} \right)\,\left( {\displaystyle{\Lambda \over {{\alpha _H} + {\mu _H}}} + 1} \right).}$$
$$\eqalign{R_0^2 = & \left( {\displaystyle{\Lambda \over {{\theta _M} + {\mu _M} + {c_M}}} + 1} \right)\,\left( {\displaystyle{\Lambda \over {{\theta _H} + {\mu _H}}} + 1} \right)\, \cr & \left( {\displaystyle{\Lambda \over {{\theta _M} + {c_M}}} + 1} \right)\,\left( {\displaystyle{\Lambda \over {{\alpha _H} + {\mu _H}}} + 1} \right).}$$
This equation, or rather a simplified version of it, was obtained in [Reference Favier13–Reference Massad15]. This technique assumes a force of infection Λ > 0 and, therefore, no value of the control parameter, c M (which Pinho et al. [Reference Pinho5] added to the adult mortality rate, μ M ), can reduce R 0 below unity. To investigate the case in which Λ < 0 and, therefore, R 0 < 1, another method must be used, as described in [Reference Massad15]. Therefore, Pinho et al.'s conclusion that ‘other strategies would be necessary besides the adult vector-control […] to reduce the force of infection’ cannot be deduced from their equation (3.8) and is, in fact, wrong. Again, we stress that Macdonald's threshold would be useless if Pinho et al.'s [Reference Pinho5] conclusion were true.
When R 0 < 1, as explained in [Reference Massad15, Reference Burattini, Coutinho and Massad16], although an outbreak can occur, it will naturally fade away.
We shall return to the above method of estimating R 0. Here we only mention that this method is correct if the disease is introduced in a small portion of the region, as it usually is, that is going to be invaded. This is because the exponential growth is deduced by assuming that the disease is introduced in a uniform region. However, as we shall see in Appendix I, when introduced in just a small portion of the region, the development of the disease proceeds as a wave. Since what is usually reported is the number of cases per unit time (epidemiological week, for instance) this method can only be used if the disease propagates slowly in space because (see Appendix I) the entire epidemic curve is not exponential but is so only in the very first initial phase.
Finally, to end this section, we note that the sensitivity of the mortality rates of mosquito phases was investigated in [Reference Amaku10, Reference Massad17, Reference Massad and Coutinho18]. From these papers, we conclude that the adult mosquito mortality rate is the parameter to which R 0 (and also the force of infection) is, by far, most sensitive. Compared with the aquatic phase mortality rate, this is rather intuitive because, in equilibrium, killing one mosquito prevents the appearance of hundreds of eggs and other aquatic phases, whereas killing one egg prevents the appearance of just one mosquito. Orders of magnitude of the relative effect between control measures directed against mosquitoes vs. control measures directed against eggs were given in [Reference Amaku10]. In this paper, we compared the sensitivity of R 0, the force of infection and the steady-state prevalence to the control parameters. In general, the sensitivity to control measures (increase of mortality rates) directed against mosquitoes is more efficient by 2–3 orders of magnitude. However, these calculations did not take into account the logistic and financial costs of any of the above-mentioned strategies.
BACKWARD BIFURCATIONS
In an influential and interesting paper, Garba et al. [Reference Garba, Gumel and Abu Bakar6] claim that a model very similar to the one given by equation (1) exhibits so-called backward bifurcation (subcritical bifurcation). In this section, we find the stationary solutions of system (1) and prefer not to call the observed phenomena backward bifurcation. We examine this very interesting system from a different point of view and also discuss the possible origin of the phenomena exhibited by Garba et al.'s model [Reference Garba, Gumel and Abu Bakar6].
The stationary solution for the prevalence of the infection in humans, I H /N H , is obtained by replacing the derivatives on the right side of the system (1) equations and solving the resulting nonlinear system of equations. The results (see [Reference Amaku10, Reference Amaku19] for more details) are:
 $$\displaystyle{{{I_H}} \over {{N_H}}} = \displaystyle{{({\gamma _M} + g{\mu _M}){a^2}bc{\textstyle{{{N_M}} \over {{N_H}}}} - Q\left( {{\mu _M} + {\gamma _M}} \right)\,{\mu _M}(1 - g)} \over {({\gamma _M} + g{\mu _M}){a^2}bc{\textstyle{{{N_M}} \over {{N_H}}}}Z + acQ\left( {{\mu _M} + {\gamma _M}} \right)}},\,$$
$$\displaystyle{{{I_H}} \over {{N_H}}} = \displaystyle{{({\gamma _M} + g{\mu _M}){a^2}bc{\textstyle{{{N_M}} \over {{N_H}}}} - Q\left( {{\mu _M} + {\gamma _M}} \right)\,{\mu _M}(1 - g)} \over {({\gamma _M} + g{\mu _M}){a^2}bc{\textstyle{{{N_M}} \over {{N_H}}}}Z + acQ\left( {{\mu _M} + {\gamma _M}} \right)}},\,$$
which is the equilibrium prevalence of the infection in humans, where
and
To obtain equation (9), we assumed a logistic birth (or immigration) rate for Λ H
where r H is the per capita birth (or immigration) rate of humans and K H is the carrying capacity of humans.
The stationary solution for the total human population, N H , is
where
 $$\left.\eqalign{A = & \;ac{r_H}\Omega\comma \cr B = & - ac\Omega {K_H}\left( {{r_H} - {\mu _H}} \right) + \Gamma Z{r_H}\cr &- \Omega {\mu _M}\left( {1 - g} \right)\,{\alpha _H}{K_H} \comma\cr C = & - \Gamma {K_H}\left( {{r_H} - {\mu _H}} \right)\,Z + \Gamma {\alpha _H}{K_H}.}\right\} $$
$$\left.\eqalign{A = & \;ac{r_H}\Omega\comma \cr B = & - ac\Omega {K_H}\left( {{r_H} - {\mu _H}} \right) + \Gamma Z{r_H}\cr &- \Omega {\mu _M}\left( {1 - g} \right)\,{\alpha _H}{K_H} \comma\cr C = & - \Gamma {K_H}\left( {{r_H} - {\mu _H}} \right)\,Z + \Gamma {\alpha _H}{K_H}.}\right\} $$
and
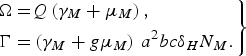 $$\left.\eqalign{\Omega = & Q\left( {{\gamma _M} + {\mu _M}} \right)\comma \cr \Gamma = & \left( {{\gamma _M} + g{\mu _M}} \right)\,{a^2}bc{\delta _H}{N_M}.}\right\} $$
$$\left.\eqalign{\Omega = & Q\left( {{\gamma _M} + {\mu _M}} \right)\comma \cr \Gamma = & \left( {{\gamma _M} + g{\mu _M}} \right)\,{a^2}bc{\delta _H}{N_M}.}\right\} $$
The stationary solution for the specific case of dengue prevalence in humans, I H /N H , is obtained by making δ H → ∞ and θ H = σ H = 0 in equation (9)
 $$\eqalign{\displaystyle{{{I_H}} \over {{N_H}}} = \displaystyle{ \matrix{({\gamma _M} + g{\mu _M}){a^2}bc{\textstyle{{{N_M}} \over {{N_H}}}} - \left( {{\mu _H} + {\gamma _H} + {\alpha _H}} \right)\cr \left( {{\mu _M} + {\gamma _M}} \right)\,{\mu _M}(1 - g)} \over \matrix{({\gamma _M} + g{\mu _M}){a^2}bc{\textstyle{{{N_M}} \over {{N_H}}}}\left( {1 + {\textstyle{{{\gamma _H}} \over {{\mu _H}}}}} \right) \cr + \;ac\left( {{\mu _H} + {\gamma _H} + {\alpha _H}} \right)\,\left( {{\mu _M} + {\gamma _M}} \right)} }}.$$
$$\eqalign{\displaystyle{{{I_H}} \over {{N_H}}} = \displaystyle{ \matrix{({\gamma _M} + g{\mu _M}){a^2}bc{\textstyle{{{N_M}} \over {{N_H}}}} - \left( {{\mu _H} + {\gamma _H} + {\alpha _H}} \right)\cr \left( {{\mu _M} + {\gamma _M}} \right)\,{\mu _M}(1 - g)} \over \matrix{({\gamma _M} + g{\mu _M}){a^2}bc{\textstyle{{{N_M}} \over {{N_H}}}}\left( {1 + {\textstyle{{{\gamma _H}} \over {{\mu _H}}}}} \right) \cr + \;ac\left( {{\mu _H} + {\gamma _H} + {\alpha _H}} \right)\,\left( {{\mu _M} + {\gamma _M}} \right)} }}.$$
The basic reproduction number can be deduced by making the numerator of the previous equation equal to zero, resulting in equation (5).
In the specific case of dengue, the value of N H reduces to:
 $${N_{H,\,d}} = \displaystyle{{ - {B_d} + \sqrt {B_d^2 - 4{A_d}{C_d}}} \over {2{A_d}}},$$
$${N_{H,\,d}} = \displaystyle{{ - {B_d} + \sqrt {B_d^2 - 4{A_d}{C_d}}} \over {2{A_d}}},$$
where
 $$\left.\eqalign{{A_d} = & \;ac{r_H}{\Omega _d}\comma \cr {B_d} = & - ac{\Omega _d}{K_H}\left( {{r_H} - {\mu _H}} \right) + \Gamma {Z_d}{r_H} \cr&- {\Omega _d}{\mu _M}\left( {1 - g} \right)\,{\alpha _H}{K_H}\comma \cr {C_d} = & - \Gamma {K_H}\left( {{r_H} - {\mu _H}} \right)\,{Z_d} + \Gamma {\alpha _H}{K_H}. }\right\} $$
$$\left.\eqalign{{A_d} = & \;ac{r_H}{\Omega _d}\comma \cr {B_d} = & - ac{\Omega _d}{K_H}\left( {{r_H} - {\mu _H}} \right) + \Gamma {Z_d}{r_H} \cr&- {\Omega _d}{\mu _M}\left( {1 - g} \right)\,{\alpha _H}{K_H}\comma \cr {C_d} = & - \Gamma {K_H}\left( {{r_H} - {\mu _H}} \right)\,{Z_d} + \Gamma {\alpha _H}{K_H}. }\right\} $$
and
 $$\left.\eqalign{{\Omega _d} = & \;\left( {{\mu _H} + {\gamma _H} + {\alpha _H}} \right)\,\left( {{\gamma _M} + {\mu _M}} \right)\comma \, \cr {Z_d} = &\; \left( {1 + \displaystyle{{{\gamma _H}} \over {{\mu _H}}}} \right).}\right\} $$
$$\left.\eqalign{{\Omega _d} = & \;\left( {{\mu _H} + {\gamma _H} + {\alpha _H}} \right)\,\left( {{\gamma _M} + {\mu _M}} \right)\comma \, \cr {Z_d} = &\; \left( {1 + \displaystyle{{{\gamma _H}} \over {{\mu _H}}}} \right).}\right\} $$
Equation (17) does not show any backward bifurcation.
A possible misprint in Garba et al.'s [Reference Garba, Gumel and Abu Bakar6] paper results from writing Λ H [their equation (1)] as
The correct equation should have N H instead of N M in the denominator because, as can be noted in system (1), the total number of bites inflicted by infected mosquitoes is a(I M +η M L M ), a fraction of which, S H /N H , are on susceptible humans, of which a fraction b is actually infective.
Garba et al.'s [Reference Garba, Gumel and Abu Bakar6] assumption that the total number of bites that mosquitoes inflict in people is, of course, equal to the total number of bites that people receive is correct. However, the force of infection from mosquito to human, ab/N H (I M + η M LM ), depends on b, whereas the force of infection from human to mosquito, ac/N H (I H + η H LH ), depends on c. Therefore, equation (4) in Garba et al.'s [Reference Garba, Gumel and Abu Bakar6] paper is correct only in the particular case when b = c. In addition, Garba et al. [Reference Garba, Gumel and Abu Bakar6] assumed that susceptible and infected mosquitoes bite with different rates, although this is not explicitly used in their model. The points mentioned in the above remarks on Garba et al.'s [Reference Garba, Gumel and Abu Bakar6] paper have no influence on the existence of backward bifurcation. We mention these facts for completeness and to describe the Garba et al. [Reference Garba, Gumel and Abu Bakar6] paper fairly, i.e. describing all the biological realities that they introduce in their model.
To compare our model with that in the paper by Garba et al. [Reference Garba, Gumel and Abu Bakar6], in more detail, we take, Λ H = const., instead of the one given by equation (13), and make Λ M also constant. The system can be solved, and the stationary state value of I H /N H (the translation to Garba et al.'s [Reference Garba, Gumel and Abu Bakar6] notation is shown in Appendix II) is:
 $$\displaystyle{{{I_H}} \over {{N_H}}} = \displaystyle{{ - {B_g} \pm \sqrt {B_g^2 - 4{A_g}{C_g}}} \over {2{A_g}}},\,$$
$$\displaystyle{{{I_H}} \over {{N_H}}} = \displaystyle{{ - {B_g} \pm \sqrt {B_g^2 - 4{A_g}{C_g}}} \over {2{A_g}}},\,$$
where
 $$\left.\eqalign{&{A_g} = \displaystyle{{C_{HM}^2 {\,f_1}} \over {{\mu _V}}}Q{B_ *} ({B_ *} - {\alpha _M})\cr &\;\qquad+ {C_{MH}}C_{HM}^2 f_1^2 {\,f_2}\displaystyle{{{N_M}} \over {{N_H}}}\, {B_ *} \displaystyle{{(Q - {\alpha _H})} \over {{\mu _H}}}\comma \cr &{B_g}={C_{HM}}{\,f_1}QB_ * ^2 + {C_{MH}}{C_{HM}}{\,f_1}{\,f_2}\displaystyle{{{N_M}} \over {{N_H}}} \cr &\;\,\qquad {B_ *} \displaystyle{{{\mu _M}} \over {{\mu _H}}}(Q - {\alpha _H}) - {C_{MH}}C_{HM}^2 f_1^2 {\,f_2}\displaystyle{{{N_M}} \over {{N_H}}}{B_ *} \cr &\,\qquad+ Q{B_ *} {C_{HM}}{\,f_1}({B_ *} - {\alpha _M})\comma \cr &{C_g} = - {C_{MH}}{C_{HM}}{\,f_1}{\,f_2}\displaystyle{{{N_M}} \over {{N_H}}}{B_ *} {\mu _M} + QB_ * ^2 {\mu _M}\comma \cr &{B_ *} = \,\displaystyle{{\left( {{\mu _M} + {\gamma _M}} \right)\,\left( {{\mu _M} + {\alpha _M}} \right)} \over {{\gamma _M}}} \comma \cr &Q = \,\displaystyle{{\left( {{\mu _H} + {\delta _H}} \right)\,\left( {{\mu _H} + {\gamma _H} + {\alpha _H}} \right)} \over {{\delta _H}}}\comma \cr &{\,f_1} = \, 1 + \displaystyle{{{\eta _H}} \over {{\delta _H}}}\left( {{\mu _H} + {\gamma _H} + {\alpha _H}} \right)\,\comma \cr &{\,f_2} = \,1 + \displaystyle{{{\eta _M}} \over {{\gamma _M}}}\left( {{\mu _M} + {\alpha _M}} \right)\,\comma \cr &{C_{MH}} = \; ab\comma \cr &{C_{HM}} = \;ac.}\right\} $$
$$\left.\eqalign{&{A_g} = \displaystyle{{C_{HM}^2 {\,f_1}} \over {{\mu _V}}}Q{B_ *} ({B_ *} - {\alpha _M})\cr &\;\qquad+ {C_{MH}}C_{HM}^2 f_1^2 {\,f_2}\displaystyle{{{N_M}} \over {{N_H}}}\, {B_ *} \displaystyle{{(Q - {\alpha _H})} \over {{\mu _H}}}\comma \cr &{B_g}={C_{HM}}{\,f_1}QB_ * ^2 + {C_{MH}}{C_{HM}}{\,f_1}{\,f_2}\displaystyle{{{N_M}} \over {{N_H}}} \cr &\;\,\qquad {B_ *} \displaystyle{{{\mu _M}} \over {{\mu _H}}}(Q - {\alpha _H}) - {C_{MH}}C_{HM}^2 f_1^2 {\,f_2}\displaystyle{{{N_M}} \over {{N_H}}}{B_ *} \cr &\,\qquad+ Q{B_ *} {C_{HM}}{\,f_1}({B_ *} - {\alpha _M})\comma \cr &{C_g} = - {C_{MH}}{C_{HM}}{\,f_1}{\,f_2}\displaystyle{{{N_M}} \over {{N_H}}}{B_ *} {\mu _M} + QB_ * ^2 {\mu _M}\comma \cr &{B_ *} = \,\displaystyle{{\left( {{\mu _M} + {\gamma _M}} \right)\,\left( {{\mu _M} + {\alpha _M}} \right)} \over {{\gamma _M}}} \comma \cr &Q = \,\displaystyle{{\left( {{\mu _H} + {\delta _H}} \right)\,\left( {{\mu _H} + {\gamma _H} + {\alpha _H}} \right)} \over {{\delta _H}}}\comma \cr &{\,f_1} = \, 1 + \displaystyle{{{\eta _H}} \over {{\delta _H}}}\left( {{\mu _H} + {\gamma _H} + {\alpha _H}} \right)\,\comma \cr &{\,f_2} = \,1 + \displaystyle{{{\eta _M}} \over {{\gamma _M}}}\left( {{\mu _M} + {\alpha _M}} \right)\,\comma \cr &{C_{MH}} = \; ab\comma \cr &{C_{HM}} = \;ac.}\right\} $$
It is easy to demonstrate that one of the roots of equation (21) is negative. Making the positive solution equal to zero, we can deduce the threshold. In fact, the threshold (and therefore R
0) can be deduced by making
![]() $ - {B_g} + \sqrt {B_g^2 - 4{A_g}{C_g}} = 0$
, i.e. C
g
= 0. The result is
$ - {B_g} + \sqrt {B_g^2 - 4{A_g}{C_g}} = 0$
, i.e. C
g
= 0. The result is
 $${R_0} = \displaystyle{{{C_{MH}}{C_{HM}}{\,f_1}{\,f_2}{\textstyle{{{N_M}} \over {{N_H}}}}{\gamma _M}{\delta _H}} \over {\left( {{\mu _M} + {\gamma _M}} \right)\,\left( {{\mu _M} + {\alpha _M}} \right)\,\left( {{\mu _H} + {\delta _H}} \right)\,\left( {{\mu _H} + {\gamma _H} + {\alpha _H}} \right)}}.$$
$${R_0} = \displaystyle{{{C_{MH}}{C_{HM}}{\,f_1}{\,f_2}{\textstyle{{{N_M}} \over {{N_H}}}}{\gamma _M}{\delta _H}} \over {\left( {{\mu _M} + {\gamma _M}} \right)\,\left( {{\mu _M} + {\alpha _M}} \right)\,\left( {{\mu _H} + {\delta _H}} \right)\,\left( {{\mu _H} + {\gamma _H} + {\alpha _H}} \right)}}.$$
This value of R 0 can also be deduced by linearizing the system (1), using Garba et al.'s [Reference Garba, Gumel and Abu Bakar6] notation, around the trivial solution (no disease). The value of N M /N H is crucial. Garba et al. [Reference Garba, Gumel and Abu Bakar6] use Λ M μH /Λ H μ M (see [Reference Garba, Gumel and Abu Bakar6, p. 14]). However, to obtain the other points in their figure 2, it is necessary to increase the initial value of N M with respect to N H . This is what we think Garba et al. [Reference Garba, Gumel and Abu Bakar6] did: they varied the parameters and calculated R 0 using N M /NH = Λ M μ H /Λ H μ M , but introduced infected mosquitoes into the initial condition. Introducing infected mosquitoes into the initial condition changes R 0 by increasing N M /N H . Therefore, the values given by R 0 in Figure 2 are actually greater than 1.

Fig. 2. The three behaviours of the system described in the text.
Consider the value of R 0 [equation (23)]. Because the disease affects both populations involved, we must note that, if N M /N H calculated at time t = 0 makes R 0 > 1, then the disease will invade the population in the sense that immediately after 0 the values of I M and I H will be greater than their values at t = 0.
If the disease invades the population, two things can happen. If the value N M (t)/N H (t) is such that, at some value of t, the value of R 0 falls below 1, the disease will disappear. If this does not happen, the disease will go to the steady state. This depends on the initial condition. For the values given by Garba et al. [Reference Garba, Gumel and Abu Bakar6], who do not use densities, the transition occurs for S V (0) = 2717.8445, E V (0) = 0, I V (0) = 100, S H (0) = 511.82, E H (0) = 0, I H (0) = 1, R H (0) = 0. Note that without disease, the equilibrium values are N V = 1875 and N H = 512.82. The resulting figure is shown below.
A summary of the above results will now be given. First, we define a function of t, R(t), as
 $${R(t) = \displaystyle{{{C_{MH}}{C_{HM}}{\,f_1}{\,f_2}{\textstyle{{{N_M}(t)} \over {{N_H}(t)}}}{\gamma _M}{\delta _H}} \over {\left( {{\mu _M} + {\gamma _M}} \right)\,\left( {{\mu _M} + {\alpha _M}} \right)\,\left( {{\mu _H} + {\delta _H}} \right)\,\left( {{\mu _H} + {\gamma _H} + {\alpha _H}} \right)}}.}$$
$${R(t) = \displaystyle{{{C_{MH}}{C_{HM}}{\,f_1}{\,f_2}{\textstyle{{{N_M}(t)} \over {{N_H}(t)}}}{\gamma _M}{\delta _H}} \over {\left( {{\mu _M} + {\gamma _M}} \right)\,\left( {{\mu _M} + {\alpha _M}} \right)\,\left( {{\mu _H} + {\delta _H}} \right)\,\left( {{\mu _H} + {\gamma _H} + {\alpha _H}} \right)}}.}$$
We can understand the behaviour of this system by using this function as explained below.
-
(1) If R(t = 0) (which happens to be R 0) is less than 1, then the disease will not invade (see the two lowest curves in Fig. 2);
-
(2) If R(t = 0) is greater than 1, the disease will invade the population, but we have to distinguish between two cases:
-
(3) There is a threshold value for N M (0)/N H (0), below which case (2.1) occurs and above which case (2.2) occurs. We found this threshold numerically but we suspect that, by using Garba et al.'s [Reference Garba, Gumel and Abu Bakar6] method, this can be obtained analytically.
In Appendix II, we show in detail why we prefer not to call the phenomena described above and in Garba et al.'s [Reference Garba, Gumel and Abu Bakar6] paper a backward bifurcation, as is suggested by Garba et al. [Reference Garba, Gumel and Abu Bakar6].
CONCLUSIONS
Mathematical models in sciences must have their complexity adjusted to their goals, and, as we have seen, we have basically two classes of models. At one extreme we have models that are intended to check if our intuition about why a certain phenomenon occurs is correct. This model must be as simple as possible, otherwise it may fail. An example of such a model is a model designed to test dengue overwintering [Reference Coutinho4]. At the other extreme, we have models whose goals are to predict future outcomes. These models are necessarily very complex. An example of such a model (for dengue vaccination) is given by [Reference Coudeville and Garnett20]. Of course there are models in between these classes.
In this paper, the model belonging to the second class of models (to estimate the basic reproduction number from the initial phase of the infection) fails by not including sufficient complexities that are necessary to deal with the data.
We have seen in Appendix I why the effects of the spatial distribution of a vector-borne infection should be taken into account when estimating the basic reproduction number from the initial size of the epidemics. Another crucial effect that has to be taken into account is that the size and duration of the epidemic depend on the initial distribution of the invasion of the infection, i.e. where and how it was introduced in a given region previously free of the infection.
The model belonging to the first class that is examined in this paper is one that tries to clarify the role of the so-called backward bifurcation. In the ‘Backward bifurcations’ section, we examined in detail the paper by Garba et al. [Reference Garba, Gumel and Abu Bakar6] which analyses this possible role of the so-called backward bifurcation in dengue.
To summarize the above considerations, we list some recommendations, using vector-borne diseases models, to avoid some of our misgivings about the use of models:
-
(1) Complicated models of vector-borne infections should be used when attempting to make predictions about future events. They are error-prone if not all necessary biological realities are included otherwise their predictions may be unreliable. Many models of vector-borne diseases are designed to estimate parameters that are important to plan control measures. In the example we use in this paper, the estimation of the basic reproduction number from the initial phase of an epidemic is examined and examples of biological realities that should be included are given. Alternatively, we suggested another method to collect data: ideally a uniform region should be chosen with both populations uniformly distributed and only count cases from this region, from the beginning of the outbreak. Because people commute into and out this region, the above method underestimates the basic reproduction number. This error depends on the size of the region that should be carefully estimated. The region cannot be too large because of the propagation of epidemic waves as explained above. On the other hand, it cannot be too small to minimize the effect of people commuting into and out of the region. We plan to publish details of how to choose such a region in another paper. We should stress that most published calculations of the basic reproduction number are not bad approximations of R 0, but should be carefully interpreted to account for error bounds.
-
(2) Models that have as a goal examination of the mechanism behind certain phenomenon should be as simply as possible. The model of this type examined in this paper deals with the existence of backward bifurcation. The model has, perhaps, too many variables. For instance, differential mortality in humans by dengue is known to be small and in the model studied is perhaps the cause of the so-called backward bifurcation. We conclude that this additional mortality should have not been introduced in the model for dengue. Of course the model may be useful for other diseases.
APPENDIX I. The initial condition
As explained before, most models of vector-borne infections assume (sometimes without saying so) that the variables are population densities and usually homogeneously distributed over a sufficiently large area. This approach has two problems: the first, solved in this Appendix, is that modifications of this model are needed before it can be applied to situations where inhomogeneous populations occur; the second problem is that authors usually assume that the disease is also introduced into the region in a uniformly distributed manner. In fact, the disease is introduced in a small area of the region and the disease propagates through the region as a wave [Reference Lopez21]. Let us explain the latter statement in detail.
When the disease is introduced in a virgin area (village, city, etc.), it is introduced in a small geographical area of this region and then propagates as a wave to other places of the region. Since what is usually reported is the number of cases per unit time (epidemiological week, for instance) the method discussed in the ‘Estimating R 0 …’ section can only be used if the disease propagates slowly in space. This is the reason why only a few points of the epidemic curve can be used. When not used properly, the method can fail to produce a good measure of the basic reproduction number and in any case the number so derived applies only to the small region where the infection was introduced. Of course if the region is uniform this number is valid for the whole region. In this Appendix we show how to model the propagation of the infection although in this paper this is done in a very sketchy manner; however, this is important as explained above. However, the propagation of an epidemic throughout a region is of central importance in understanding the infection dynamics and in interpreting the available data. It is extremely difficult to include the mobility of humans and vector populations and we suspect that in some cases no general statements can be made. This section, however, is important in highlighting that some general consequences can already be deduced without investigating in detail some points, namely, land use, population density, overlay, etc.
In this Appendix, we compare the outcomes of two epidemics, one of which assumes that the disease is introduced uniformly in the region and the second which assumes the disease is introduced in just a small area and then propagates. Thus, by comparing the two results we can estimate the effect of the fact that epidemics usually start in small regions.
We begin estimating this effect on a one-dimensional road of length D. In the case in which we assume that the disease is introduced uniformly, the system of equations (1) can be numerically integrated, and the resulting epidemic compared. To calculate the effect of introducing the disease in just small regions, the system of equations (1) has to be modified to consider the spatial dimension. Let S H (x,t)dx be the number of susceptible humans living between x and x + dx at time t. The other variables are defined similarly.
 $$\left.\eqalign{\displaystyle{{\partial {S_H}(x,\,t)} \over {\partial t}} = & - {\lambda _H}(x,\,t){S_H}(x,\,t) - {\mu _H}{S_H}(x,\,t)\cr &+ {\Lambda _H}(x,\,t)\comma \cr \displaystyle{{\partial {L_H}(x,\,t)} \over {\partial t}} = &\; {\lambda _H}(x,\,t){S_H}(x,\,t) - ({\mu _H} + {\gamma _H}){L_H}(x,\,t)\comma \cr \displaystyle{{\partial {I_H}(x,\,t)} \over {\partial t}} = & \;{\gamma _H}{L_H}(x,\,t) - ({\mu _H} + {\alpha _H} + {\delta _H}){I_H}(x,\,t)\comma \cr \displaystyle{{\partial {R_H}(x,\,t)} \over {\partial t}} = & \;{\delta _H}{I_H}(x,\,t) - {\mu _H}{R_H}(x,\,t)\comma \cr \displaystyle{{\partial {S_M}(x,\,t)} \over {\partial t}} = & - {\lambda _M}(x,\,t){S_M}(x,\,t) - {\mu _M}{S_M}(x,\,t) \cr & + {\Lambda _M}(x,\,t)\comma \cr \displaystyle{{\partial {L_M}(x,\,t)} \over {\partial t}} = & \;{\lambda _M}(x,\,t){S_M}(x,\,t) - ({\mu _M} + {\gamma _M}){L_M}(x,\,t)\comma \cr \displaystyle{{\partial {I_M}(x,\,t)} \over {\partial t}} = & \;{\gamma _M}{L_M}(x,\,t) - {\mu _M}{I_M}(x,\,t).\,}\right\}$$
$$\left.\eqalign{\displaystyle{{\partial {S_H}(x,\,t)} \over {\partial t}} = & - {\lambda _H}(x,\,t){S_H}(x,\,t) - {\mu _H}{S_H}(x,\,t)\cr &+ {\Lambda _H}(x,\,t)\comma \cr \displaystyle{{\partial {L_H}(x,\,t)} \over {\partial t}} = &\; {\lambda _H}(x,\,t){S_H}(x,\,t) - ({\mu _H} + {\gamma _H}){L_H}(x,\,t)\comma \cr \displaystyle{{\partial {I_H}(x,\,t)} \over {\partial t}} = & \;{\gamma _H}{L_H}(x,\,t) - ({\mu _H} + {\alpha _H} + {\delta _H}){I_H}(x,\,t)\comma \cr \displaystyle{{\partial {R_H}(x,\,t)} \over {\partial t}} = & \;{\delta _H}{I_H}(x,\,t) - {\mu _H}{R_H}(x,\,t)\comma \cr \displaystyle{{\partial {S_M}(x,\,t)} \over {\partial t}} = & - {\lambda _M}(x,\,t){S_M}(x,\,t) - {\mu _M}{S_M}(x,\,t) \cr & + {\Lambda _M}(x,\,t)\comma \cr \displaystyle{{\partial {L_M}(x,\,t)} \over {\partial t}} = & \;{\lambda _M}(x,\,t){S_M}(x,\,t) - ({\mu _M} + {\gamma _M}){L_M}(x,\,t)\comma \cr \displaystyle{{\partial {I_M}(x,\,t)} \over {\partial t}} = & \;{\gamma _M}{L_M}(x,\,t) - {\mu _M}{I_M}(x,\,t).\,}\right\}$$
where
and
In equation (26), a β H (x,x′) is the number of bites per unit time that I M (x′,t)dx′ infected mosquitoes inflict in S H (x,t)dx susceptible humans (note that infected mosquitoes are in position x′ and susceptible humans are in position x). Similarly, in equation (a β M (x,x′) is the number of bites per unit time that S M (x′,t)dx′ susceptible mosquitoes inflict in I H (x,t)dx infected humans (susceptible mosquitoes are in position x′ and infected humans are in position x). As a first approximation, we may assume that β H (x,x′) and β M (x,x′) are the same functions. For simplicity, we also assume that β H (x,x′) = β H (|x−x′|) and β M (x,x′) = β M (|x−x′|) are functions of the distance |x−x′ only.
The standard way to solve system (25) is by choosing one of its variables [say, I H (x,t) and writing an integral equation for it. The result in this case is an integral equation with 16 terms that will be analysed in a future publication.
We can, however, estimate the phenomena we are investigating by selecting a less complicated system [Reference Lopez21] that describes a simple SIR model, given by equation (3) of the above reference.
As mentioned by Postnikov & Sokolov [Reference Postnikov and Sokolov22, pp. 209], equations (3), (4) and (10) of [Reference Lopez21] are more general than the equations most commonly seen in the literature.
In a two-dimensional region, which, for simplicity, will be considered circular, the system of equations (25) is modified by replacing x with r, the distance from an arbitrary point to the centre, and adding an angular variable θ. Thus, S H (r,θ,t)ds is the number of susceptible humans living in a small area ds = r dr dθ around the point (r, θ) at time t. This unfolds similarly for the other variables.
On the other hand, equations (26) and (27) become
 $$\eqalign{&{\lambda _H}(r,\,\theta, \,t) = \displaystyle{1 \over N_H}\mathop {\int}\nolimits_0^D r^{\prime}dr^{\prime} \mathop {\int}\nolimits_0^{2\pi} d\theta^{\prime} ab{\beta _H}\cr&\quad\times\left( {\sqrt {{r^2} + {r^{^{\prime}2}} - 2rr^{\prime}\cos (\theta - \theta^{\prime})}} \right)\,{I_M}(r^{\prime},\,\theta^{\prime},\,t)},$$
$$\eqalign{&{\lambda _H}(r,\,\theta, \,t) = \displaystyle{1 \over N_H}\mathop {\int}\nolimits_0^D r^{\prime}dr^{\prime} \mathop {\int}\nolimits_0^{2\pi} d\theta^{\prime} ab{\beta _H}\cr&\quad\times\left( {\sqrt {{r^2} + {r^{^{\prime}2}} - 2rr^{\prime}\cos (\theta - \theta^{\prime})}} \right)\,{I_M}(r^{\prime},\,\theta^{\prime},\,t)},$$
and
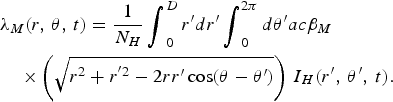 $$\eqalign{&{\lambda _M}(r,\,\theta, \,t) =\displaystyle{1 \over N_H}\mathop {\int}\nolimits_0^D r^{\prime}dr^{\prime}\mathop {\int}\nolimits_0^{2\pi} d\theta^{\prime} ac{\beta _M}\cr&\quad\times\left( {\sqrt {{r^2} + {r^{^{\prime}2}} - 2rr^{\prime}\cos (\theta - \theta^{\prime})}} \right)\,{I_H}(r^{\prime},\,\theta^{\prime},\,t).}$$
$$\eqalign{&{\lambda _M}(r,\,\theta, \,t) =\displaystyle{1 \over N_H}\mathop {\int}\nolimits_0^D r^{\prime}dr^{\prime}\mathop {\int}\nolimits_0^{2\pi} d\theta^{\prime} ac{\beta _M}\cr&\quad\times\left( {\sqrt {{r^2} + {r^{^{\prime}2}} - 2rr^{\prime}\cos (\theta - \theta^{\prime})}} \right)\,{I_H}(r^{\prime},\,\theta^{\prime},\,t).}$$
Returning to the one-dimensional case, we obtain, by solving numerically equation (10) of reference [Reference Lopez21], the results reproduced in Figure 3a
for the case where the initial condition covers the entire road. The epidemic,
![]() $I(t) = \int_0^L {I(x,t)}dx$
, consists of a huge peak that almost disappears and later returns after a significantly long time. This is not what is observed in the real world.
$I(t) = \int_0^L {I(x,t)}dx$
, consists of a huge peak that almost disappears and later returns after a significantly long time. This is not what is observed in the real world.

Fig. 3. Numerical solution for the one-dimensional case when: (a) the initial condition covers the entire road; (b) the disease is introduced on one end of the road. Figures not to the same scale.
When the disease is introduced only at one end of the road, Figure 3b
shows the epidemic [number of cases vs. time t, i.e.
![]() $I(t) = \int_0^L I(x,\,t)dx$
]. In this case, we can see that the epidemic rises much slower and lasts for a very long time, being interrupted only if seasonality is considered. This can be understood in the following way: the epidemic wave travels from, for example, the left side of the road to the right side. The epidemic that started because of the initial condition, at the left side, vanishes, but it is still recorded by the cases that are happening on the wave front. It may happen that the disease reappears on the left side before the wave reaches the right side. We then have the impression that the disease reaches steady state.
$I(t) = \int_0^L I(x,\,t)dx$
]. In this case, we can see that the epidemic rises much slower and lasts for a very long time, being interrupted only if seasonality is considered. This can be understood in the following way: the epidemic wave travels from, for example, the left side of the road to the right side. The epidemic that started because of the initial condition, at the left side, vanishes, but it is still recorded by the cases that are happening on the wave front. It may happen that the disease reappears on the left side before the wave reaches the right side. We then have the impression that the disease reaches steady state.
Returning to the case of the calculation of R 0 from the initial phase of the outbreak, we can see that, in nature, the disease is frequently introduced in a small part of the environment and that because of what was stated above, one has to consider only the very beginning of the outbreak. Alternatively, we can modify the way data are collected. Ideally one should choose a uniform region with both populations uniformly distributed and collect cases only from this region from the beginning of the outbreak. Because people commute into and out this region, the above method underestimates the basic reproduction number. This error depends on the size of the region that should be carefully estimated. Other challenges of introducing spatial heterogeneities in epidemic models are qualitatively analysed in [Reference Riley8].
APPENDIX II. Further comments on Garba et al.'s [Reference Garba, Gumel and Abu Bakar6] findings
For a more detailed comparison with the paper by Garba et al. [Reference Garba, Gumel and Abu Bakar6], we consider the following system of differential equations:
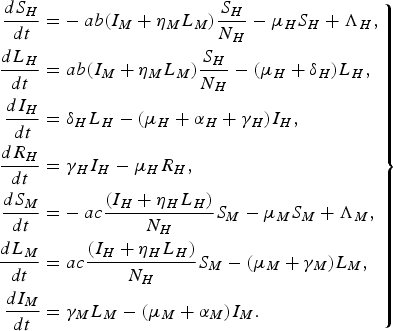 $$\left.\eqalign{\displaystyle{{d{S_H}} \over {dt}} = & - ab({I_M} + {\eta _M}{L_M})\displaystyle{{{S_H}} \over {{N_H}}} - {\mu _H}{S_H} + {\Lambda _H}\comma \cr \displaystyle{{d{L_H}} \over {dt}} = & \;ab({I_M} + {\eta _M}{L_M})\displaystyle{{{S_H}} \over {{N_H}}} - ({\mu _H} + {\delta _H}){L_H}\comma \cr \displaystyle{{d{I_H}} \over {dt}} = & \;{\delta _H}{L_H} - ({\mu _H} + {\alpha _H} + {\gamma _H}){I_H}\comma \cr \displaystyle{{d{R_H}} \over {dt}} = & \;{\gamma _H}{I_H} - {\mu _H}{R_H}\comma \cr \displaystyle{{d{S_M}} \over {dt}} = & - ac\displaystyle{{({I_H} + {\eta _H}{L_H})} \over {{N_H}}}{S_M} - {\mu _M}{S_M} + {\Lambda _M}\comma \cr \displaystyle{{d{L_M}} \over {dt}} = & \;ac\displaystyle{{({I_H} + {\eta _H}{L_H})} \over {{N_H}}}{S_M} - ({\mu _M} + {\gamma _M}){L_M}\comma \cr \displaystyle{{d{I_M}} \over {dt}} = & \; {\gamma _M}{L_M} - ({\mu _M} + {\alpha _M}){I_M}.}\right\} $$
$$\left.\eqalign{\displaystyle{{d{S_H}} \over {dt}} = & - ab({I_M} + {\eta _M}{L_M})\displaystyle{{{S_H}} \over {{N_H}}} - {\mu _H}{S_H} + {\Lambda _H}\comma \cr \displaystyle{{d{L_H}} \over {dt}} = & \;ab({I_M} + {\eta _M}{L_M})\displaystyle{{{S_H}} \over {{N_H}}} - ({\mu _H} + {\delta _H}){L_H}\comma \cr \displaystyle{{d{I_H}} \over {dt}} = & \;{\delta _H}{L_H} - ({\mu _H} + {\alpha _H} + {\gamma _H}){I_H}\comma \cr \displaystyle{{d{R_H}} \over {dt}} = & \;{\gamma _H}{I_H} - {\mu _H}{R_H}\comma \cr \displaystyle{{d{S_M}} \over {dt}} = & - ac\displaystyle{{({I_H} + {\eta _H}{L_H})} \over {{N_H}}}{S_M} - {\mu _M}{S_M} + {\Lambda _M}\comma \cr \displaystyle{{d{L_M}} \over {dt}} = & \;ac\displaystyle{{({I_H} + {\eta _H}{L_H})} \over {{N_H}}}{S_M} - ({\mu _M} + {\gamma _M}){L_M}\comma \cr \displaystyle{{d{I_M}} \over {dt}} = & \; {\gamma _M}{L_M} - ({\mu _M} + {\alpha _M}){I_M}.}\right\} $$
We intend to show that the above system presents a threshold that has a branch with negative values.
In the case of dengue, the disease-induced mortality rates in the populations, α M in the vector population and α H in the human population, are usually assumed to be zero. In the calculations below, we keep those as different from zero, for completeness.
The stationary solution for human prevalence is given by
 $${A_1}{\left( {\displaystyle{{{I_H}} \over {{N_H}}}} \right)^2} + {A_2}\left( {\displaystyle{{{I_H}} \over {{N_H}}}} \right) + {A_3} = 0,$$
$${A_1}{\left( {\displaystyle{{{I_H}} \over {{N_H}}}} \right)^2} + {A_2}\left( {\displaystyle{{{I_H}} \over {{N_H}}}} \right) + {A_3} = 0,$$
where
 $$\left.\eqalign{{A_1} = &\; \displaystyle{{{a^2}{c^2}f_H^2} \over {{\mu _M}}}XY\left( {Y - {\alpha _M}} \right) + {a^2}bcf_H^2 {\,f_M}\displaystyle{{{N_M}} \over {{N_H}}}\cr&\times Y\displaystyle{{(X - {\alpha _H})} \over {{\mu _H}}}\comma \cr {A_2} = & \;ac{\,f_H}X{Y^2} + {a^2}bc{\,f_H}{\,f_M}\displaystyle{{{N_M}} \over {{N_H}}}Y\displaystyle{{{\mu _M}} \over {{\mu _H}}}(X - {\alpha _H}) \cr&- acY{\,f_H}\left( {{a^2}b{\,f_H}{\,f_M}\displaystyle{{{N_M}} \over {{N_H}}} - XY + {\alpha _M}X} \right)\,\comma \cr {A_3} = & \;Y{\mu _M}\left( { - {a^2}bc{\,f_H}{\,f_M}\displaystyle{{{N_M}} \over {{N_H}}} + XY} \right)\,\comma \cr X = & \;\displaystyle{{({\mu _H} + {\delta _H})({\mu _H} + {\gamma _H} + {\alpha _H})} \over {{\delta _H}}}\comma \cr Y = & \;\displaystyle{{({\mu _M} + {\gamma _M})\left( {{\mu _M} + {\alpha _M}} \right)} \over {{\gamma _M}}}.}\right\}$$
$$\left.\eqalign{{A_1} = &\; \displaystyle{{{a^2}{c^2}f_H^2} \over {{\mu _M}}}XY\left( {Y - {\alpha _M}} \right) + {a^2}bcf_H^2 {\,f_M}\displaystyle{{{N_M}} \over {{N_H}}}\cr&\times Y\displaystyle{{(X - {\alpha _H})} \over {{\mu _H}}}\comma \cr {A_2} = & \;ac{\,f_H}X{Y^2} + {a^2}bc{\,f_H}{\,f_M}\displaystyle{{{N_M}} \over {{N_H}}}Y\displaystyle{{{\mu _M}} \over {{\mu _H}}}(X - {\alpha _H}) \cr&- acY{\,f_H}\left( {{a^2}b{\,f_H}{\,f_M}\displaystyle{{{N_M}} \over {{N_H}}} - XY + {\alpha _M}X} \right)\,\comma \cr {A_3} = & \;Y{\mu _M}\left( { - {a^2}bc{\,f_H}{\,f_M}\displaystyle{{{N_M}} \over {{N_H}}} + XY} \right)\,\comma \cr X = & \;\displaystyle{{({\mu _H} + {\delta _H})({\mu _H} + {\gamma _H} + {\alpha _H})} \over {{\delta _H}}}\comma \cr Y = & \;\displaystyle{{({\mu _M} + {\gamma _M})\left( {{\mu _M} + {\alpha _M}} \right)} \over {{\gamma _M}}}.}\right\}$$
When A 3 = 0, we have
which is equivalent to
 $$\displaystyle{{{a^2}b{c_H}{\,f_M}{\textstyle{{{N_M}} \over {{N_H}}}}{\gamma _M}{\delta _H}} \over {{\mu _M}({\mu _M} + {\gamma _M})({\mu _H} + {\delta _H})({\mu _H} + {\gamma _H} + {\alpha _H})}} = 1,\,$$
$$\displaystyle{{{a^2}b{c_H}{\,f_M}{\textstyle{{{N_M}} \over {{N_H}}}}{\gamma _M}{\delta _H}} \over {{\mu _M}({\mu _M} + {\gamma _M})({\mu _H} + {\delta _H})({\mu _H} + {\gamma _H} + {\alpha _H})}} = 1,\,$$
the threshold condition for the basic reproduction number is R 0 = 1. In this case (A 3 = 0), the coefficient A 2 becomes
 $$\eqalign{{A_2} = &\; ac{\,f_H}X{Y^2} + {a^2}bc{\,f_H}{\,f_M}\displaystyle{{{N_M}} \over {{N_H}}}Y\displaystyle{{{\mu _M}} \over {{\mu _H}}}(X - {\alpha _H}) \cr&- acXY{\,f_H}{\alpha _M} = ac{\,f_H}XY(Y - {\alpha _M}) \cr&+ {a^2}bc{\,f_H}{\,f_M}\displaystyle{{{N_M}} \over {{N_H}}}Y\displaystyle{{{\mu _M}} \over {{\mu _H}}}(X - {\alpha _H}).} $$
$$\eqalign{{A_2} = &\; ac{\,f_H}X{Y^2} + {a^2}bc{\,f_H}{\,f_M}\displaystyle{{{N_M}} \over {{N_H}}}Y\displaystyle{{{\mu _M}} \over {{\mu _H}}}(X - {\alpha _H}) \cr&- acXY{\,f_H}{\alpha _M} = ac{\,f_H}XY(Y - {\alpha _M}) \cr&+ {a^2}bc{\,f_H}{\,f_M}\displaystyle{{{N_M}} \over {{N_H}}}Y\displaystyle{{{\mu _M}} \over {{\mu _H}}}(X - {\alpha _H}).} $$
For A 3 = 0, one root of I H /N H is zero and the second root of equation (31) is
The expression for X−α H is
and the expression for Y−α M is
Both X−α H and Y−α M are positive, and, as a consequence, the coefficients A 1 and A 2 are positive. Hence, the second root [equation (36)] of I H /N H is negative. Thus, we prefer not to call the interesting findings by Garba et al. [Reference Garba, Gumel and Abu Bakar6] a backward bifurcation. Our interpretation of the phenomena observed by Garba et al. is described in the present paper in the last four paragraphs of the section ‘Backward bifurcations’.
The translation from the notation of this paper to the notation used by Garba et al. [Reference Garba, Gumel and Abu Bakar6] is presented in Tables 4 and 5.
Table 4. Translation from the notation of this paper to the notation used by Garba et al. for the variables

Table 5. Translation from the notation of this paper to the notation used by Garba et al. for the parameters

The results obtained by Garba et al. [Reference Garba, Gumel and Abu Bakar6] may not be entirely correct because they come from writing λ H [their equation (1)] as
The correct equation should have N H instead of N M in the denominator because, as can be noted in system (1), the total number of bites inflicted by infected mosquitoes is a(I M + η M L M ), a fraction S H /N H of which are on susceptible humans, of which a fraction b is actually infective. Therefore, as mentioned previously, equation (4) in Garba et al.'s [Reference Garba, Gumel and Abu Bakar6] paper is correct only if b = c.
ACKNOWLEDGEMENTS
This work was partially supported by LIM01 HCFMUSP, Fapesp, CNPq, Dengue Tools under the Seventh Framework Programme of the European Community, grant agreement no. 282589, and MS/FNS (grant no. 27835/2012).
DECLARATION OF INTEREST
None.











