INTRODUCTION
Disease simulation models are widely used as decision support tools to aid in planning for disease outbreaks, predicting or assessing outbreaks in real-time and as training tools in simulation exercises [Reference Boklund1, Reference Gloster2]. Simulation models can offer valuable insights into the effectiveness of different control strategies and act as important decision support tools by comparing and evaluating outbreak scenarios and control strategies [Reference Morris3–Reference Garner and Hamilton5]. Decision makers need to have confidence that advice based on model outputs is reliable if models are to be used to inform disease control policy. Underlying assumptions and model limitations also need to be made transparent and communicated effectively to decision makers.
Criticism of the use and value of modelling is not uncommon [Reference de Jong6, Reference Kitching7]. Careful evaluation of a model is important to ensure it represents the real-life system appropriately, is fit for purpose, and its operation and outputs are transparent and well communicated to decision makers. Part of this evaluation includes model verification, a process that checks whether a model is correctly implemented and matches underlying assumptions and specifications relative to the model concept. This may involve a structured assessment of the programme, checking the model with experts, examining model outputs for ‘correctness’, and comparing models against others under the same set of starting parameters [Reference Garner and Hamilton5]. A number of studies have used this latter approach [Reference Boklund1, Reference Gloster2, Reference Dubé8, Reference Sanson9]. Model validation checks the accuracy of a model's representation of the real system. As explained in Dubé et al. [Reference Dubé8] ‘an infectious disease model is said to be internally valid when its outputs make epidemiological sense given the underlying population dataset and parameters used to initiate the simulations. External validity is assessed when model predictions are comparable with one or more real epidemics.’
Spanning 2005–2010, members of the Quadrilateral Group of countries (QUADS: Australia, Canada, New Zealand, USA) were involved in a study comparing foot-and-mouth (FMD) simulation models [Reference Dubé8]. Building on this experience, a new study on the use of vaccination in FMD control was initiated through QUADS, and also included the UK and The Netherlands. The study used a multi-model comparison approach to compare different vaccination strategies in a FMD outbreak based on the UK's 2010 FMD simulation exercise, ‘Exercise Silver Birch’ [10]. Exercise Silver Birch was chosen as it provided a plausible multi-focal outbreak and ready-to-use data. Each model was set up and parameterized to represent the scenario. Parameter input values for the models reflected UK settings and FMD contingency plans to ensure consistency between models and their outputs. The study aimed to compare models under a common scenario, and understand how these model differences might influence the effectiveness of vaccination in controlling an FMD outbreak.
The use of vaccination to augment control of an FMD outbreak in a previously FMD-free country is increasingly being recognized as a potentially important component of the response. This is particularly so when standard zoo-sanitary measures have been unsuccessful in eradicating the disease and community concern over the large-scale slaughter of animals has grown, as was seen in the recent Korean [Reference Sakamoto11] and Japanese FMD outbreaks [Reference Akashi12]. Recent changes in the international guidelines on regaining FMD-free status following an outbreak have also reduced the time period before countries can regain their FMD-free status when using vaccination [13]. Many countries have or are developing contingency plans and vaccine supply arrangements. However, there is considerable uncertainty as to when and how vaccination should be used, and how vaccinated animals should be managed. For countries with significant exports of livestock and livestock products this is of particular concern, because under the current conditions the presence of FMD-vaccinated animals in the population could be expected to cause market access difficulties [Reference Boklund1]. Under a ‘vaccinate-to-live’ policy, where vaccinated animals remain in the population, FMD-free status can be recovered 6 months after the last reported case, compared to 3 months under a ‘stamping-out’ policy [13]. Although a 3-month recovery period applies in a ‘vaccinate-to-cull’ policy, market delays are expected due to the added surveillance requirements for proof of freedom status and delays in removing vaccinates following the outbreak [Reference Boklund1]. Consequently, this is an important issue for policy planners and disease managers.
The success of a vaccination programme to control FMD is expected to vary depending on the approach taken, response goals and programme management. A number of recently published articles demonstrate the various vaccination approaches that can be used in the control of FMD [Reference Boklund1, Reference Dürr14–Reference Backer16]. For this study, advice was sought from disease managers in the participating countries and directly from chief veterinary officers at the 2012 QUADS Annual Meeting in Canada. The key factors that were considered for a vaccination programme included the vaccination approach (suppressive vs. protective), timing (when vaccination is carried out relative to the date of first detection), species to vaccinate, vaccination zone sizes, deployment methods, and resourcing. These factors were used to develop a series of 12 control strategies suitable for each model's configuration and requirements. A model comparison approach was used to evaluate the effectiveness of the strategies in controlling a FMD outbreak in the UK. The study also aimed to identify and explain any differences in results between models.
MATERIALS AND METHODS
FMD models
Models from five countries participated in the study:
-
(1) AusSpread – Australian Department of Agriculture [Reference Garner and Beckett4, Reference Roche17, Reference Beckett and Garner18]. AusSpread is a stochastic spatial simulation model that simulates the spread and control of FMD in livestock populations at a regional scale. AusSpread uses the farm as its unit of interest and FMD transmission is modelled through five discrete pathways: farm-to-farm animal movements, local spread (infection of farms within close geographical proximity by unspecified means), indirect contact (via contaminated fomites or animal products), animal movements via saleyards or markets and windborne spread. For FMD control, AusSpread is configured to support the range of mitigations described in Australia's contingency plans for FMD with the effectiveness of these measures dependent on resources [19].
-
(2) NAADSM – North American Animal Disease Spread Model (NAADSM) Development Team [Reference Harvey20]. NAADSM is a stochastic, spatial, state-transition simulation model designed to simulate the spread and control of highly contagious diseases between herds in a population of susceptible animals. User-established parameters define model behaviour in terms of disease progression; disease spread by direct contact, indirect contact, and windborne dissemination; and the application of control measures such as quarantine, movement restrictions, depopulation, and vaccination. NAADSM has been developed through a continuing international collaboration involving researchers from the USA and Canada, along with support, involvement, and advice from a broad international pool of subject-matter experts.
-
(3) InterSpread Plus (IS+). IS+ is a spatial and stochastic simulation model of infectious disease in domestic animal populations [Reference Sanson21, Reference Stevenson22]. IS+ is a state-transition model [Reference Isham23] meaning that the epidemiological units of interest (farm locations) exist in either the susceptible, infected and not-at-risk state at any given time. Similar to AusSpread and NAADSM, IS+ uses a series of user-defined parameters to define the spread of infectious agent from one farm location to another: local spread, windborne spread, and direct and indirect contacts. Control measures such as depopulation, vaccination, and movement restrictions in addition to varying disease surveillance intensity can be simulated, with the ability to carry out each of these activities subject to user-defined resource constraints.
-
(4) Exodis. Exodis-FMD™ is a stochastic, spatial, state-transition simulation model for FMD outbreaks in the UK. Virus transmission is simulated between and within herds, which are represented to an individual species level. User-defined epidemiological parameters are used to describe disease progression and transmission. Control measures for FMD are explicitly included in the model as specified in the UK FMD Disease Control Strategy for Great Britain (Defra, crown copyright 2011). Exodis was developed by Risk Solutions after the 2001 FMD epidemic in the UK, commissioned by the Department for Environment, Food and Rural Affairs (Defra), with the involvement of technical experts.
-
(5) The Netherlands model (NL) – Central Veterinary Institute of Wageningen UR [Reference Backer16, Reference Backer24]. NL is an individual-based stochastic spatial simulation model that describes FMD virus transmission on two levels: between animals and between herds. Results from vaccination and transmission experiments serve to parameterize the transmission model between animals, whereas the parameters for the between-herd model are estimated from the 2001 FMD epidemic in The Netherlands. The model distinguishes between cattle, sheep and pigs, and takes the relative infectivity and susceptibility of herd types and assortative mixing between herd types into account.
All models simulate the spread of disease between farms; however, the Exodis and NL models also simulate the spread of disease within farms. The remaining models approximated this process by using prevalence curves for each farm type to represent the varying infection pressure generated by an infected farm over time. The first three models can be described as micro-simulation models where discrete spread pathways are used to simulate FMD transmission – including direct animal movements, indirect contact transmission between farms, local spread, and windborne spread. For more details on these models refer to Dubé et al. [Reference Dubé8]. The NL model uses a single spatial kernel where all transmission routes are aggregated with a probability of transmission depending on the distance between infected and susceptible farms. Exodis takes a hybrid approach using a spatial kernel to represent local spread and indirect contact transmission and separate pathways for windborne spread and direct animal movement transmission.
Three of the models used in this study (AusSpread, IS+, NAADSM) have been used previously in various model comparison studies [Reference Gloster2, Reference Dubé8–Reference Sanson9]. For the remaining models, this study provided an opportunity to compare models through a relative validation process [Reference Sanson9].
Outbreak scenario
Data from the 2010 UK FMD exercise, Exercise Silver Birch, was used as the basis for the study [10]. The exercise was based on a multifocal outbreak with detailed outbreak history and documented spread of disease that could be used by the modelling teams to set up their respective models. The UK provided population data and transmission parameter values. During the set-up phase the capabilities of each model were discussed and parameter estimates and control strategies defined so that each team could configure their model to represent the same set of epidemiological assumptions and inputs. Individual models attempted to follow these settings as closely as possible, but due to model differences it was not always possible to represent the start-up conditions exactly. Where results varied significantly between models these differences are considered in the Discussion.
The study area represented 38 counties in central England and Wales. The population data was derived from the 2006 UK census with almost 65 000 premises comprising dairy, beef, sheep, pigs, and mixed cattle, sheep and pig farms (Table 1).
Table 1. UK farm population data used in a simulated outbreak of foot-and-mouth disease in the UK
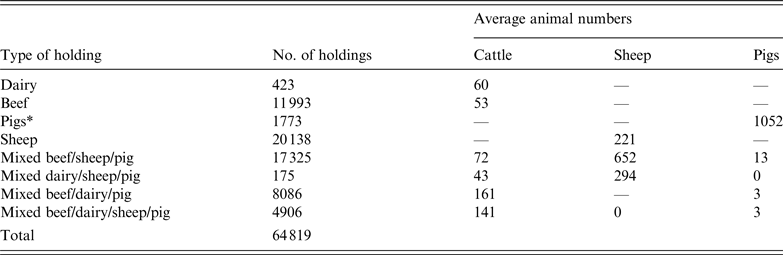
*Defined as holdings with >1000 pigs. Holdings with <1000 pigs were classified as mixed based on other species present.
Disease transmission occurred via direct contact, indirect contact, windborne and local area spread. To simplify matching of the models, long-range windborne spread was not included, because runs of Exodis during Exercise Silver Birch showed negligible numbers of cases due to that mechanism. The scenario definition used in Exercise Silver Birch included an 18-day delay from introduction until the incursion was detected by veterinary authorities (silent spread phase), by which time there were 20 undetected infected holdings in three separate foci in the study area. At the time of first detection only one infected premise (IP) had been confirmed. For consistency, this scenario was used as the initial outbreak situation for evaluating control strategies. That is, each team set up their model with the infection status and histories of these premises and all subsequent modelling scenarios began by simulating forward from the day of first detection.
Control measures
The simulated control programme was consistent with UK contingency plans [25]. It was assumed that a national livestock movement standstill would be in place for the duration of the epidemic. Control measures included livestock movement restrictions around IPs (with 100% compliance), surveillance and tracing operations, and stamping out of all FMD susceptible livestock on IPs. This approach represented the stamping-out control strategy with no vaccination (SO). Estimates of resources to conduct depopulation, surveillance and vaccination were provided by the UK. Initial estimates were subsequently reduced because they were considered overly optimistic compared to expected capacity of the other participating countries, as well as to take account of recent reductions in government-supported resources in the UK.
Vaccination strategies
To assess the effect of vaccination on FMD control, 11 vaccination strategies were defined based on a number of operational factors and taking into account the contingency plans and policy priorities in participating countries. These factors included the approach to vaccination, timing, size of vaccination zones, species vaccinated, and deployment of vaccination.
The approach to vaccination may be suppressive (SV), where at-risk animals are vaccinated within defined areas around IPs to control the spread of disease and reduce viral excretion, or protective (PV), where at-risk animals in defined areas beyond the immediate surroundings of IPs are vaccinated in advance of potential exposure to protect animals from infection [19]. The sizes of the vaccination zones evaluated were 1 km, 3 km, or 5 km in radius around IPs for SV, or a band with a 3-km inner radius and a 7-km outer radius for PV. Three delays in initiation of a vaccination programme following the first detection were considered – 1, 2 or 4 weeks. Two species-related vaccination approaches were compared: vaccination of all susceptible species or cattle-only. This was based on advice provided by disease managers. Cattle-only vaccination represents the preferred UK approach (F. Gauntlett, personal communication). Under the scenario considered, relatively few pig farms were infected compared to other species and culling was considered to be a more effective approach than vaccination for managing them. Sheep were considered a lower priority for vaccination due to their lower infectiousness, susceptibility and value compared to cattle. The deployment of vaccine could progress in a random fashion, from the outside of the ring inwards or vice versa, or vaccination of larger farms before smaller farms. The other deployment option was vaccination around all IPs from the onset of the control programme (retrospective) or only around newly declared IPs (prospective).
In total, 12 control strategies (one without vaccination and 11 with vaccination) were assessed (Table 2). The SO strategy was run for comparison and calibration of the models. It should be noted that all vaccination strategies operated in conjunction with standard zoo-sanitary measures including the culling of all FMD-susceptible animals on IPs. NAADSM could only run six of the strategies due to limitations in the model's ability to simulate the vaccination approach and deployment. For each strategy, 100 iterations were run. Each simulation was run until FMD was eradicated. The following outputs from each model were recorded:
-
(1) number of IPs;
-
(2) spatial distribution of IPs;
-
(3) outbreak duration (number of days from the start of the control programme until the last case is detected plus 21 days). It was assumed it would take 21 days following the last case to complete all decontamination, disposal, surveillance and vaccination activities;
-
(4) number of vaccinated farms.
A list of the key parameter inputs for disease spread and control measures are provided in Table 3.
Table 2. Description of the stamping-out (SO) and vaccination scenarios used in simulated outbreaks of foot-and-mouth disease in the UK
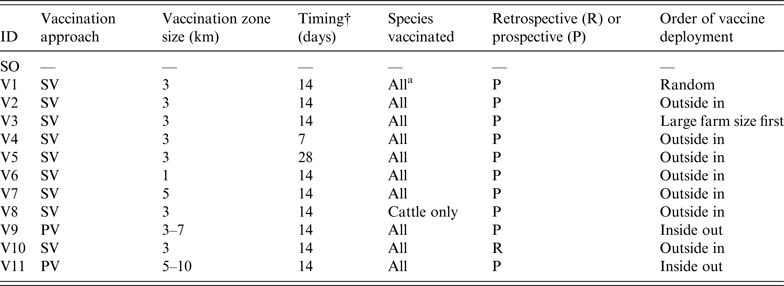
SV, Suppressive vaccination; PV, protective vaccination.
*Cattle, sheep, pigs.
†Delay between first detection in the population and initiation of a vaccination campaign.
Table 3. Key input parameters used in simulated outbreaks of foot-and-mouth disease in the UK

*Resources for vaccination do not compete with those for surveillance and culling operations.
Statistical and spatial analyses
The size of predicted outbreak areas for each iteration of each model for the 12 strategies (one SO and 11 vaccination strategies) were quantified by plotting the point locations of predicted IPs using a geographical information system (GIS). A 10-km buffer was created around each point location and contiguous buffered areas dissolved to create predicted outbreak areas. The sizes of the predicted outbreak areas (in km2) were calculated using GIS.
Strategies were organized into five logical groupings (as shown in Figs 3–7) for comparison. For each strategy group two-way ANOVAs were performed using the predicted number of IPs, the predicted epidemic duration and predicted outbreak area as the outcomes. Model (with five levels) and strategy (with three levels) were included as explanatory variables. Because outcomes from the SO strategy were expected to differ from the vaccination strategies and because it was of interest to identify differences among vaccination strategies, SO was excluded in each of the ANOVA calculations. Each of the outcome variables was log-transformed to ensure that the error values from ANOVAs were homogeneous and normally distributed.
Intensity maps showing the predicted number of infected farms/km2 were calculated using the spatstat package [Reference Baddeley and Turner26] implemented in R [27]. These analyses were performed using a regular grid of 200 × 200 cells superimposed over the study area with the standard deviation of the Gaussian kernel (the bandwidth) fixed at 10 km.
Results
Descriptive statistics of the predicted number of IPs, predicted epidemic duration (in days) and the predicted number of vaccinated farms by strategy and model are shown in Table 4. Due to the limited number of strategies completed by NAADSM, results will focus on the other four models, unless available for NAADSM.
Table 4. Results for the predicted number of infected premises, epidemic duration, and number of vaccinated farms for the control strategies used in a simulated outbreak of foot-and-mouth disease in the UK
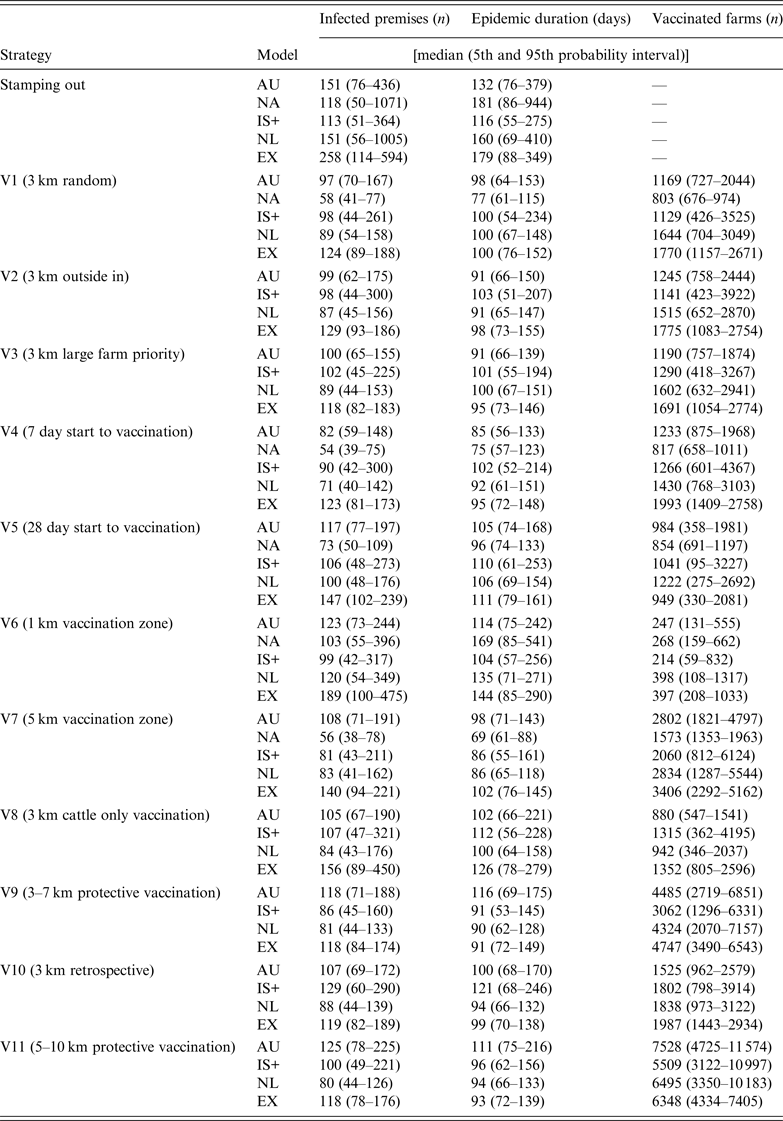
AU, AusSpread; NA, NAADSM; IS+, InterSpread Plus; NL, The Netherlands; EX, Exodis.
For the SO strategy, Exodis generated the largest epidemics in terms of the median predicted number of IPs whereas IS+ generated the smallest (Table 4). The NAADSM and NL models generated epidemics with the widest variation. Vaccination (strategies V1–V11) reduced the predicted number of IPs, epidemic duration, and variability in the outcome compared to the SO strategy (Fig. 1), with the proportional reduction in each outcome varying across each of the five models. The spatial distribution of predicted IP locations for the SO strategy varied across models (Fig. 2). AusSpread and Exodis predicted three distinct clusters of infection, IS+ predicted two, while the NAADSM and NL models predicted smaller and denser clusters of infection, with one cluster larger than the others. Similar spatial patterns were evident for each of the vaccination strategies; however; the size of the predicted outbreak areas were reduced (data not presented).

Fig. 1. Predicted median (5th and 95th probability interval) epidemic length and median (5th and 95th probability interval) number of infected premises (IPs) for 12 control strategies in a simulated outbreak of foot-and-mouth disease in the UK. Models: AU, AusSpread; EX, Exodis; IS+, InterSpread Plus; NA, NAADSM; NL, The Netherlands.
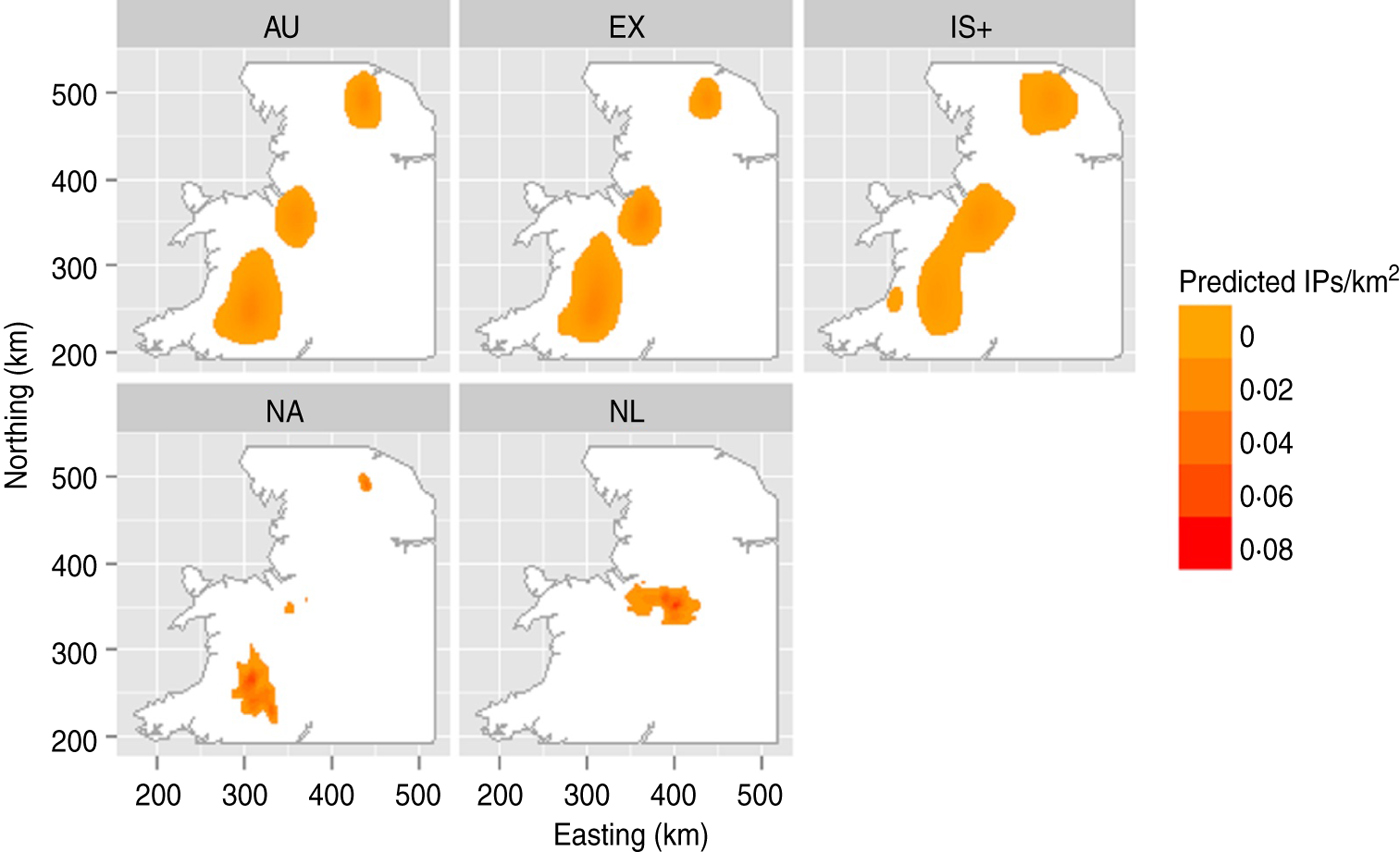
Fig. 2. Intensity of predicted infected premises for the stamping-out strategy expressed as the number of infected premises/km2 averaged across 100 iterations in a simulated outbreak of foot-and-mouth disease in the UK. Models: AU, AusSpread; EX, Exodis; IS+, InterSpread Plus; NA, NAADSM; NL, The Netherlands.
Figures 3–7 are box and whisker plots showing the ratio of the predicted number of IPs to the median number of IPs for the SO scenario computed across all models (Figs 3 a–7 a) and the ratio of predicted epidemic duration to the median epidemic duration for the SO scenario computed across all models (Figs 3 b–7 b), by scenario groupings. For all five models the order of vaccination – random (V1), outside in (V2) or large farms first (V3) did not significantly differ in terms of the predicted number of IPs (F 2,1293 = 0·958, P = 0·38, Fig. 3 a) and predicted epidemic duration (F 2,1293 = 0·697, P = 0·50, Fig. 3 b).

Fig. 3. Box and whisker plots showing: (a) the ratio of the predicted number of infected premises (IPs) to the median number of IPs for the stamping-out (SO) scenario and (b) the ratio of the predicted epidemic duration to the median epidemic duration for the SO scenario when vaccination is deployed randomly (V1), outside in (V2) or on large farms first (V3) in a simulated outbreak of foot-and-mouth disease in the UK. Models: AU, AusSpread; EX, Exodis; IS+, InterSpread Plus; NA, NAADSM; NL, The Netherlands.

Fig. 4. Box and whisker plots showing: (a) the ratio of the predicted number of infected premises (IPs) to the median number of IPs for the stamping-out (SO) scenario and (b) the ratio of the predicted epidemic duration to the median epidemic duration for the SO scenario when vaccination is started 7 days (V4), 14 days (V2), and 28 days (V5) into the control programme in a simulated outbreak of foot-and-mouth disease in the UK. Models: AU, AusSpread; EX, Exodis; IS+, InterSpread Plus; NA, NAADSM; NL, The Netherlands.

Fig. 5. Box and whisker plots showing: (a) the ratio of the predicted number of infected premises (IPs) to the median number of IPs for the stamping-out (SO) scenario and (b) the ratio of the predicted epidemic duration to the median epidemic duration for the SO scenario when vaccination radii of 1 km (V6), 3 km (V2), and 5 km (V7) are used in a simulated outbreak of foot-and-mouth disease in the UK. Models: AU, AusSpread; EX, Exodis; IS+, InterSpread Plus; NA, NAADSM; NL, The Netherlands.

Fig. 6. Box and whisker plots showing: (a) the ratio of the predicted number of infected premises (IPs) to the median number of IPs for the stamping-out (SO) scenario and (b) the ratio of the predicted epidemic duration to the median epidemic duration for the SO scenario using a suppressive approach (V2) compared to a protective approach 3–7 km (V9) or 5–10 km (V11) from identified infected places in a simulated outbreak of foot-and-mouth disease in the UK. Models: AU, AusSpread; EX, Exodis; IS+, InterSpread Plus; NA, NAADSM; NL, The Netherlands.

Fig. 7. Box and whisker plots showing: (a) the ratio of the predicted number of infected premises (IPs) to the median number of IPs for the stamping-out (SO) scenario and (b) the ratio of the predicted epidemic duration to the median epidemic duration for the SO scenario when all susceptible species are vaccinated (V2) compared to vaccinating only cattle (V8), and when retrospective vaccination is used (V10) in a simulated outbreak of foot-and-mouth disease in the UK. Models: AU, AusSpread; EX, Exodis; IS+, InterSpread Plus; NA, NAADSM; NL, The Netherlands.
All models predicted smaller numbers of IPs when vaccination start was at 7 days post-detection (V4), compared to vaccination start at 14 days (V2) and 28 days (V5) (Fig. 4 a). For all models increasing vaccination start to 28 days (V5) increased predicted epidemic duration compared to vaccination start at 7 days (V4) (Fig. 4 b).
All five models predicted that a 1-km radius vaccination zone (V6) was less effective than a 3-km radius vaccination zone (V2), (Fig. 5 a, b). In all models except IS+, increasing the radius of the vaccination zone to 5 km (V7) produced little or no benefit in terms of a reduction in the predicted number of IPs or a reduction in predicted epidemic duration. For all models, a 3-km vaccination radius (V2) resulted in, on average, between four and five times the number of vaccinated farms compared with a 1-km vaccination radius (V6) and half the number of vaccinated farms compared to a 5-km vaccination radius (V7) (Table 4).
For the suppressive (V2) and protective (V9) vaccination strategies, the predicted number of IPs varied across models (Fig. 6 a). Compared to SV (V2) all models except AusSpread predicted smaller numbers of IPs for the PV strategy (V9). For all models, more than twice the numbers of farms were vaccinated when the PV approach was used since vaccination areas were larger than those used with SV (Table 4). There was no benefit in increasing the PV radius from 3–7 km (V9) to 5–10 km (V11) with all models predicting similar numbers of IPs (Fig. 6 a).
Compared to retrospective vaccination (V10), AusSpread and IS+ predicted a smaller number of IPs when a prospective vaccination (V2) strategy was applied. Exodis predicted a larger number of IPs whereas the NL model predicted similar numbers of IPs (Fig. 7 a). The differences in predicted numbers of IPs across scenarios were statistically significant (F 2,1194 = 6·49, P < 0·01).
Vaccination of cattle only (V8) did not significantly increase the predicted number of IPs compared to vaccination of all species (V2) in all models except Exodis. Exodis predicted a greater number of IPs and epidemics of longer duration for V8 compared to V2 (Fig. 7 a, b). Predicted epidemic durations were similar across strategies V10, V2 and V8 for AusSpread, IS+ and NL models.
Discussion
Modelling the use of vaccination as an adjunct to the control of FMD has been a widely published topic in the recent scientific literature [Reference Boklund1, Reference Dürr14–Reference Roche17]. The take-home message from many of these studies is that the decision to vaccinate and choice of vaccination strategy will depend on the nature of the outbreak, availability of resources, and socioeconomic factors such as trade and public opinion. While the findings from modelling studies can provide guidance to disease managers on when and how to vaccinate, they also need confidence in the modelling tools when making these decisions. In this study we sought to explore the situations under which vaccination may be of benefit in a FMD outbreak and used five modelling platforms to test how various approaches to vaccination performed in a UK setting.
Under the UK scenario examined in this study, it was clear that vaccination used in conjunction with SO resulted in significantly smaller epidemics than for SO alone. Not only was the median size of an outbreak smaller, but all models also showed that the probability of more severe epidemics was significantly reduced under the vaccination strategies compared to SO on its own. These findings support the value of vaccination as an adjunct to zoo-sanitary measures in FMD control [Reference Barnett28]. Vaccination can limit local disease spread around IPs, and despite the delay in development of immunity, can be effective in helping to contain an outbreak. This is particularly the case when disease is widespread or fast spreading, or when authorities anticipate significant resource issues [Reference Dürr14, Reference Roche17, Reference Tomassen29, Reference Abdalla30]. Backer and co-workers [Reference Backer16] modelled FMD transmission in a dense livestock region in The Netherlands and concluded that vaccination or pre-emptive ring culling was needed as an adjunct to standard control measures. Similar findings have been seen in modelling studies of FMD outbreaks in Denmark [Reference Boklund1] and Australia [Reference Roche17].
All models showed that the earlier vaccination is implemented in a control programme the more effective it is likely to be in reducing the size of an outbreak. For this study, the earliest period before vaccine would be available for deployment in the UK was assumed to be 7 days [Reference Keeling31]. Our findings are consistent with other modelling studies that show the length of time before vaccination is used in the field is critical to its effectiveness [Reference Porphyre15, Reference Tildesley32]. Porphyre et al. [Reference Porphyre15] showed that a daily delay in using vaccination linearly reduced its effectiveness in terms of numbers of IPs, duration of epidemics, and numbers of vaccinated animals in the population.
Another common finding across the models was that among the vaccination zone sizes simulated, 3-km vaccination zones around IPs resulted in the most benefit in terms of minimizing epidemic size, duration and number of vaccinated farms in the population. Increasing vaccination zone size to 5 km did not always reduce epidemic size or duration but required the vaccination of approximately twice the number of vaccinated farms in the population. It is important to appreciate the assumptions applied in this study: that a national livestock movement standstill was in place for the duration of the control programme and that there was 100% compliance with movement controls of livestock. This means that effectively local and indirect spread were the most important mechanisms by which disease transmission could occur. In the models this is implemented either by spatial kernels (Exodis, NAADSM and NL models) or distance bands (AusSpread, IS+) that are parameterized so that a large number of the new infections tended to occur within 3 km of an IP [Reference Gibbens33], and the further a susceptible farm is from an IP the less likely it is to become infected. Given this, it is probably not surprising that vaccinating in 3-km rings around IPs proved to be effective with little benefit seen in vaccinating beyond these areas. If farms over a wider area are at risk of infection, then the use of wider rings might need to be considered. Three out of four models suggested that PV was associated with smaller outbreaks than SV, although at the cost of vaccinating more farms in total. Available resources for vaccination may have also influenced these outcomes. Some models (e.g. AusSpread and Exodis) implemented vaccination in strict accordance with the UK resource settings (Table 3) based on animal numbers on farms, with multiple teams allocated to large farms to ensure vaccination would be completed in a single day. As a result, using larger vaccination zones such as 5-km suppressive rings or 5-km protective bands, a backlog of farms waiting to be vaccinated could build up which would take some time to clear. This had the potential to reduce the benefits of vaccination. By contrast, other models used a simpler approach based on average numbers of farms able to be vaccinated per day.
Three of four models predicted that a cattle-only vaccination strategy was as effective as vaccinating all susceptible species. For these models epidemics were similar between strategies with less farms requiring vaccination under the cattle-only approach. This translates into significantly fewer animals vaccinated as many farms were mixed so only a proportion of the animals on these farms required vaccination. The value of such a strategy is that it significantly reduces the total number of animals vaccinated without compromising the size or length of the epidemic. Similar findings have been reported elsewhere [Reference Tildesley32]. There are clear advantages to using this strategy as less vaccine is needed and fewer resources are required to vaccinate stock and manage vaccinated animals over the post-outbreak phase. Restrictions in trade and management of vaccinated animals following a FMD outbreak have historically limited the use of vaccination. FMD-free status can be recovered 3 months after the last reported case under SO or a ‘vaccinate-to-cull’ strategy, where vaccinates are removed from the population, or 6 months if vaccinated animals remain in the population and surveillance to demonstrate absence of FMD circulation is undertaken [13]. In a vaccination strategy where fewer animals are vaccinated, removal of vaccinated animals or post-outbreak surveillance will be simpler and less expensive.
This study provided a means to compare different models and to assess if control strategies produced similar outcomes. This approach provides a relative validation methodology that can enhance end-user confidence in model outputs [Reference Gloster2, Reference Dubé8]. For a disease manager it can be disconcerting when different models generate different outcomes for the same type of study scenario. Where the findings are consistent, irrespective of the model used, one can have greater confidence that the outcome is not an artefact or consequence of a specific modelling team's conceptual approach or implementation. From this perspective there is value in model diversity, particularly given differences in modelling objectives, data availability and approaches to parameterization. On the other hand, where differences do occur it is important to understand why these have occurred, recognizing that all models will have their individual strengths and limitations. Provided these are made clear, the user is then in a better position to assess the findings in terms of his or her particular context.
In our study the process of relative validation was not a trivial one, and Sanson et al. [Reference Sanson9] provides a good discussion of the challenges in parameterizing and comparing different models. Developing parameters that align with each model's requirements forced each of the modelling teams to assess the way core functions were implemented in their models, and generated some useful insights. For example, partial immunity on mixed farms that house cattle and sheep in a cattle-only vaccination strategy was modelled differently between models. In AusSpread, Exodis and NL models, cattle and sheep populations on a mixed farm are discrete populations and vaccination can be implemented separately, so that mixed farms acquire a partial immunity. In IS+ partial immunity was not fully implemented in the version of the model used, and mixed farms defaulted to a susceptibility equal to the most susceptible animals on the farm, which would be the unvaccinated species. Therefore, in IS+ cattle-only vaccination only benefited cattle-only farms, where there would be full immunity applied.
All models except NL predicted three clusters of infection that reflected diffusion-like spread from the three focal points of the starting scenario. The NL model predicted only a single cluster of infection that coincided with the highest animal density. This was because the transmission kernel extends over large distances, with higher infection probabilities at shorter distances, resulting in scattered but density-driven transmission patterns. NAADSM predicted large uncertainty intervals in epidemic size and duration for the SO strategy, which was attributed to the time to detection remaining constant throughout the epidemic, whereas time to detection diminished over time in some of the other models. The study also suggests that resources for vaccination and the way these are managed are likely to be issues particularly when larger vaccination zones are considered.
Vaccination may not always provide benefits over SO depending on the nature of the epidemic and availability of resources to control it. Vaccination may compete with SO activities for resources and interfere with the effectiveness of SO when resources are limited [Reference Roche17]. In well-resourced outbreaks or areas with low livestock density SO may be more effective than vaccination as the time to develop immunity is longer than the period to complete culling operations [Reference Dürr14, Reference Ward34]. In this study, the findings regarding the effectiveness of vaccination were sensitive to the human resource settings and the way control measures were implemented in the individual models. An example of this is the way models represent surveillance and vaccination. The UK assumptions about the resource capacity to cull, vaccinate and perform surveillance activities and the speed at which this capacity is reached are unlikely to be accurate for countries with larger farm sizes and more extensive production systems such as Australia, Canada and USA. Vaccination and culling operations were assumed to be completed on each premise within 24 h. In geographically large countries farm sizes can be significantly larger and completion of these activities within 24 h is likely to be very optimistic. The implications of this 24-h assumption need to be explored further. In addition, should resource availability in the early stages of an outbreak in the UK be reduced further, the effectiveness of SO and the relative effectiveness of vaccination strategies could change.
The decision to vaccinate and choice of strategy will ultimately depend on the nature of the epidemic, available resources to control it, and objectives of the control programme. A policy of eradication and minimization of the number of animals culled may warrant a different control policy to that of eradication in the quickest time. Time out of markets may drive the choice of control measures where the management of vaccinated animals in the population post-outbreak may prolong market access due to OIE guidelines on the time to regain FMD-free status [13]. Of additional consideration, beyond the scope of this study, are the implications of post-outbreak surveillance and proof of freedom on farms that were both vaccinated and exposed to infection [Reference Backer24]. When considering control costs and export losses, vaccination may not always be the most cost-effective approach [Reference Boklund1, Reference Dürr14].
Despite the differences in absolute numbers of IPs or epidemic durations between models, the individual models tended to demonstrate similar patterns of effectiveness between the vaccination strategies evaluated. All models predicted that vaccination as an adjunct to standard zoo-sanitary measures resulted in smaller epidemics compared to SO alone. In general, it was also clear that there were advantages in vaccinating cattle-only rather than all species, using 3-km vaccination rings immediately around IPs, and starting vaccination earlier in the control programme. Although these patterns may not hold true in other study scenarios or for other countries with different animal demographics and resources, the study highlights that certain control strategies are robust despite different model configurations. These findings can be used to support and develop more effective policies for FMD control.
ACKNOWLEDGEMENTS
We thank Kim Forde-Folle (US Department of Agriculture), Neil Harvey (University of Guelph), Naya Brangenberg (NZ Ministry for Primary Industries), Tom Smylie (Canadian Food Inspection Agency), and Katie Owen (NZ Ministry for Primary Industries) for providing policy advice and input throughout the project.
DECLARATION OF INTEREST
None.














